Многогранный угол

1.

2.

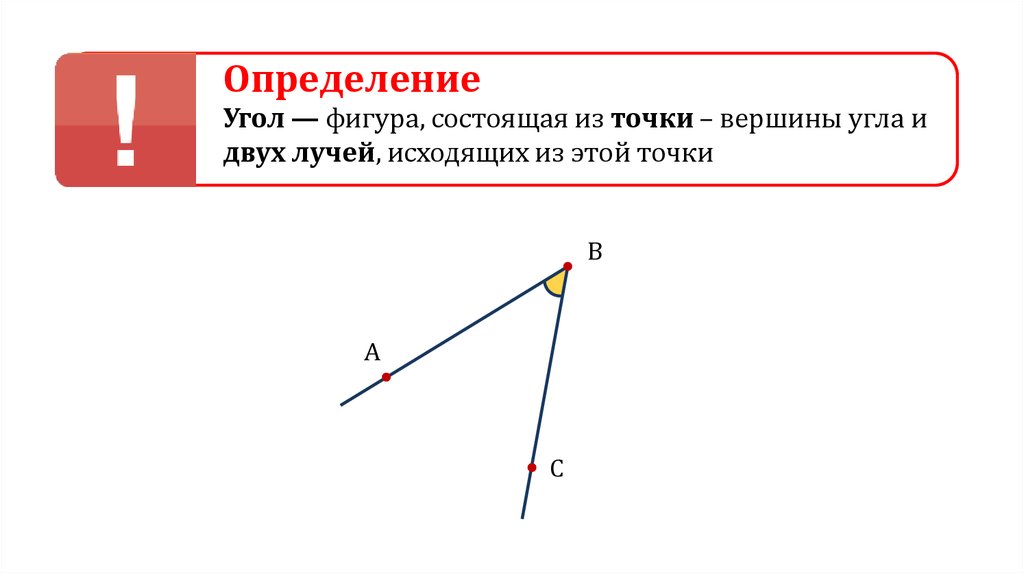
Определение
Угол — фигура, состоящая из точки – вершины угла и
двух лучей, исходящих из этой точки
B
A
C

3.

M
L
N
O
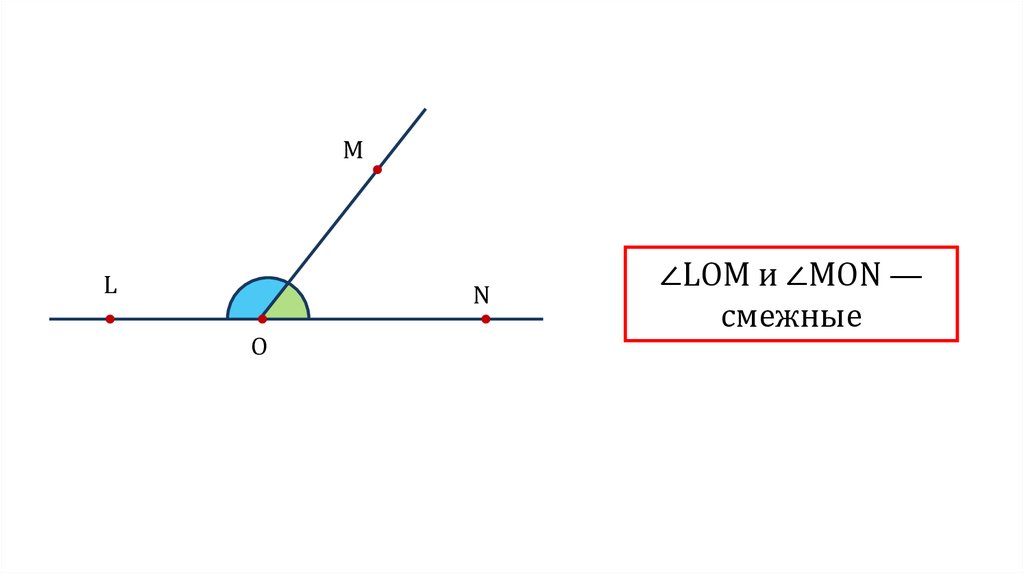
∠LOM и ∠MON —
смежные

4.

5.

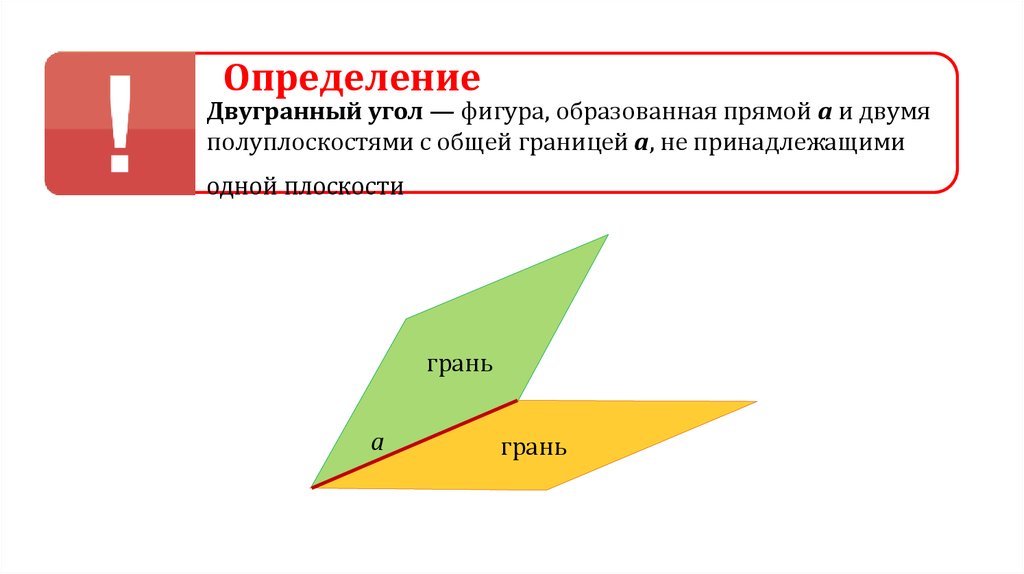
Определение
Двугранный угол — фигура, образованная прямой а и двумя
полуплоскостями с общей границей а, не принадлежащими
одной плоскости
грань
a
грань

6.

7.

O
A1
A5
An
A2
A3
A4
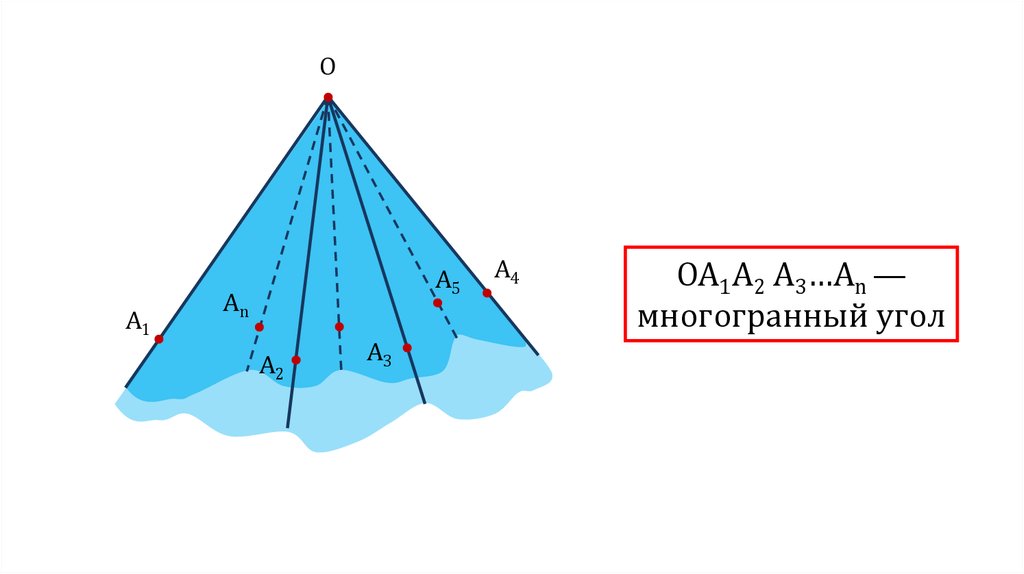
ОА1А2 А3…Аn —
многогранный угол

8.

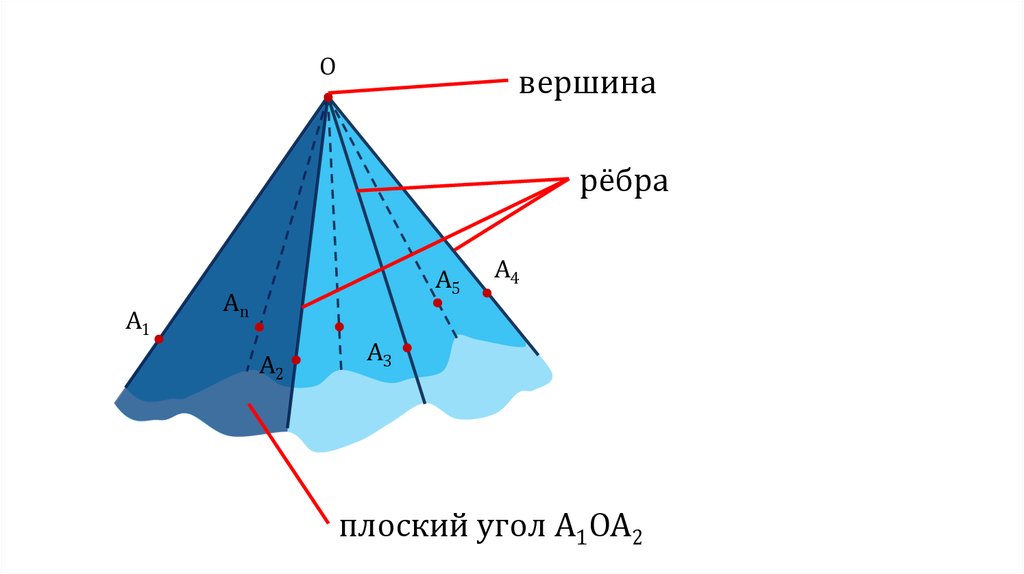
O
вершина
рёбра
A1
A5
An
A2
A4
A3
плоский угол A1OA2

9.

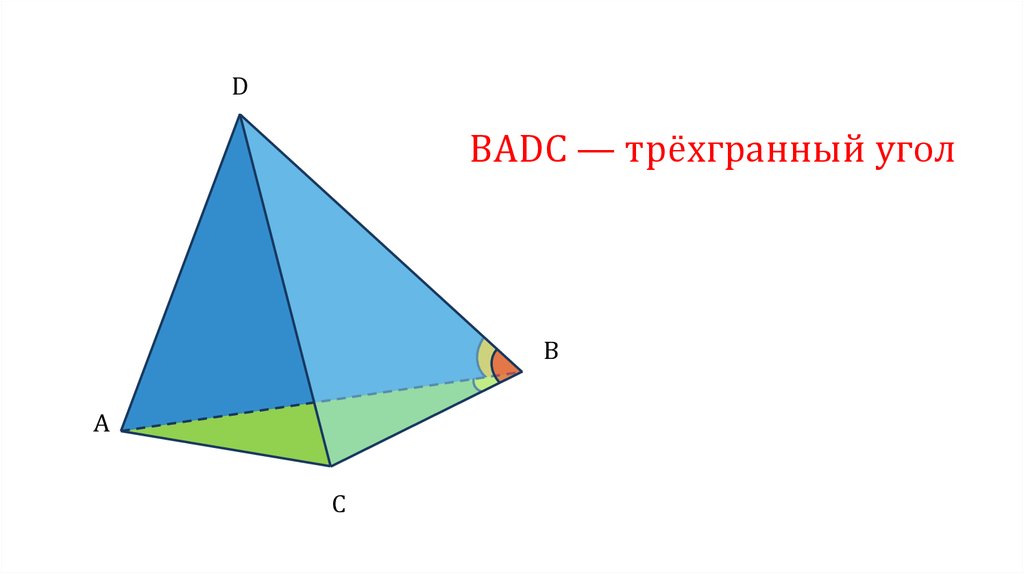
D
ВADC — трёхгранный угол
B
A
C

10.

D1
C1
A1
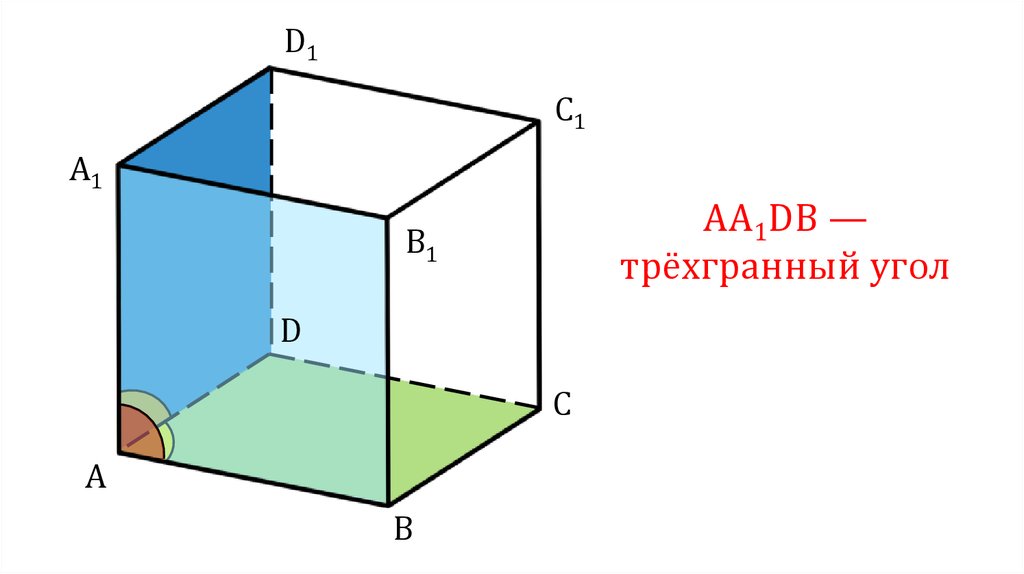
AA1DB —
трёхгранный угол
B1
D
C
A
B

11.

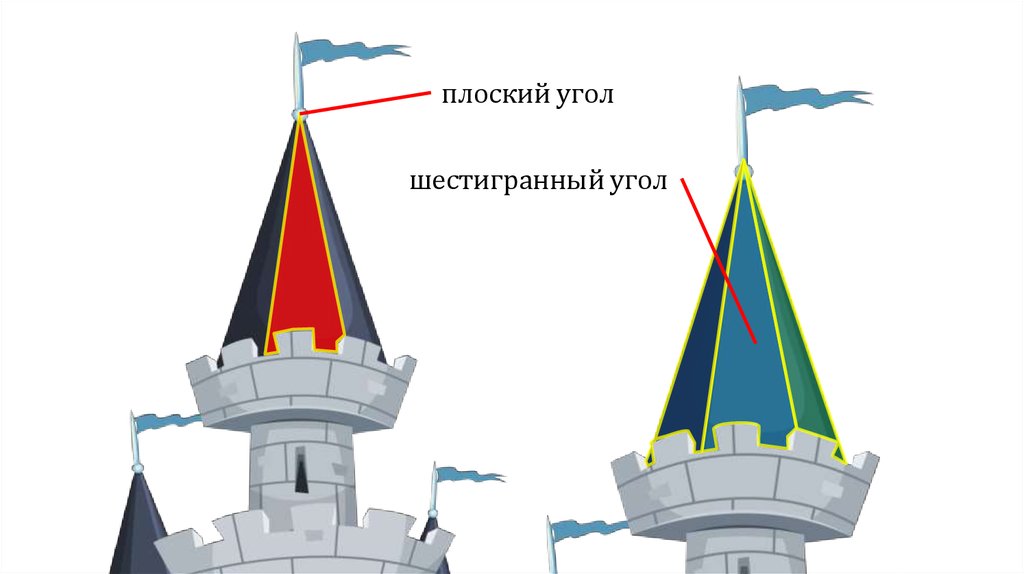
плоский угол
шестигранный угол

12.

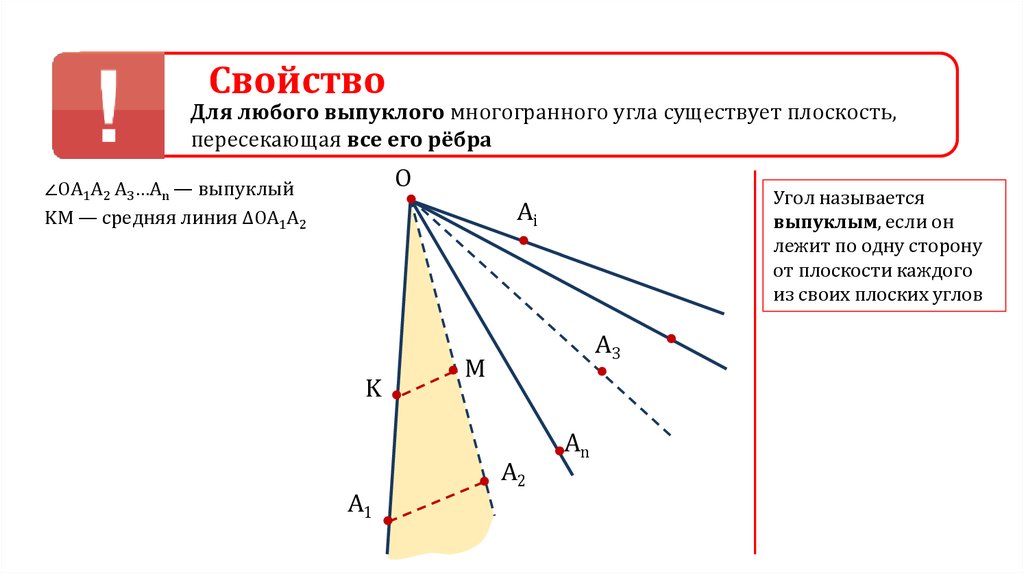
Свойство
Для любого выпуклого многогранного угла существует плоскость,
пересекающая все его рёбра
O
∠ОА1А2 А3…Аn — выпуклый
KM — средняя линия ∆ОА1А2
Угол называется
выпуклым, если он
лежит по одну сторону
от плоскости каждого
из своих плоских углов
Ai
K
A3
M
A2
A1
An

13.

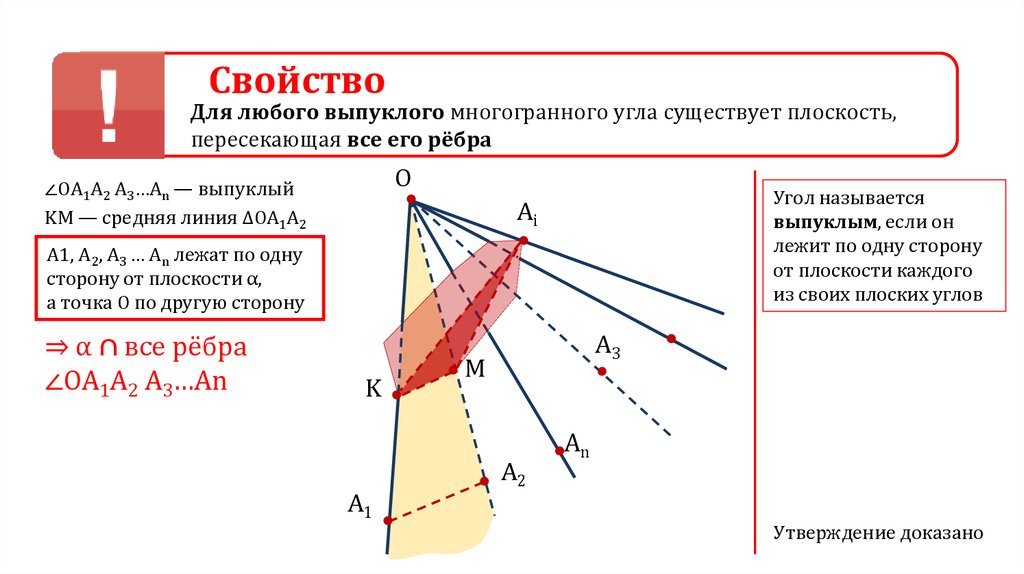
Свойство
Для любого выпуклого многогранного угла существует плоскость,
пересекающая все его рёбра
O
∠ОА1А2 А3…Аn — выпуклый
KM — средняя линия ∆ОА1А2
Угол называется
выпуклым, если он
лежит по одну сторону
от плоскости каждого
из своих плоских углов
Ai
А1, А2, А3 … Аn лежат по одну
сторону от плоскости α,
а точка О по другую сторону
⇒ α ∩ все рёбра
∠ОА1А2 А3…Аn
K
A3
M
A2
An
A1
Утверждение доказано

14.

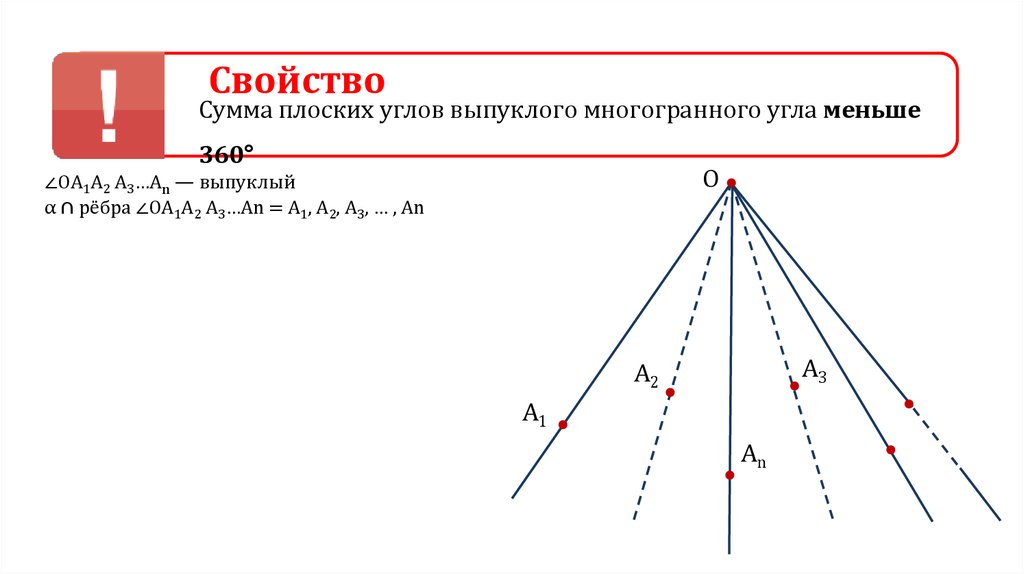
Свойство
Сумма плоских углов выпуклого многогранного угла меньше
360°
O
∠ОА1А2 А3…Аn — выпуклый
α ∩ рёбра ∠ОА1А2 А3…Аn = А1, А2, А3, … , Аn
A3
A2
A1
An

15.

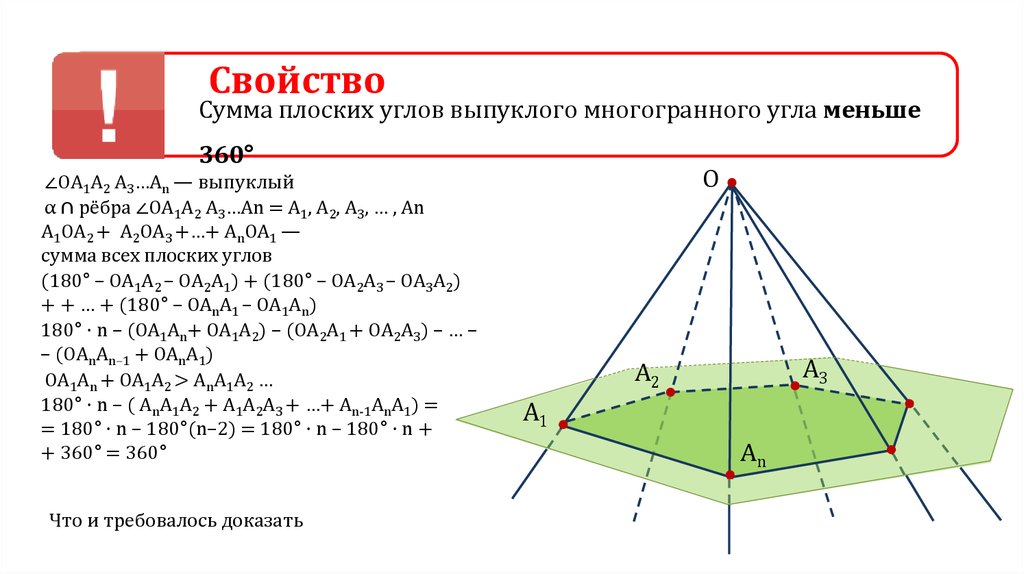
Свойство
Сумма плоских углов выпуклого многогранного угла меньше
360°
∠ОА1А2 А3…Аn — выпуклый
α ∩ рёбра ∠ОА1А2 А3…Аn = А1, А2, А3, … , Аn
А1ОА2 + А2ОА3 +…+ АnОА1 —
сумма всех плоских углов
(180° – ОА1А2 – ОА2А1) + (180° – ОА2А3 – ОА3А2)
+ + … + (180° – ОАnА1 – ОА1Аn)
180° · n – (ОА1Аn+ ОА1А2) – (ОА2А1 + ОА2А3) – … –
– (ОАnАn–1 + ОАnА1)
ОА1Аn + ОА1А2 > АnА1А2 …
180° · n – ( AnA1A2 + A1A2A3 + …+ An-1AnA1) =
= 180° · n – 180°(n–2) = 180° · n – 180° · n +
+ 360° = 360°
Что и требовалось доказать
O
A3
A2
A1
An