Гидростатика. Тема 1

1.

Пермский военный институт
войск национальной гвардии России
старший преподаватель кафедры конструкций АБТ
кандидат педагогических наук
Стрельцов Роман Вячеславович

2. Тема 2 “ГИДРОСТАТИКА”

Тема 1.Тема
Гидростатика
2
Занятие № 1 ”
“ГИДРОСТАТИКА
“Основные законы
гидростатики”

3.

Учебные вопросы
1. Статика жидкости и газа
2. Статика тела, погружённого в
жидкость

4.

ЛИТЕРАТУРА
1. Е.А.
Дундур,
Основы
машиностроительной гидравлики. Пермь., 1998 г., с.12-22.
2. А.Г. Брыксенков Аэрогидромеханика.
-М., 1978 г., с.13-22.

5.

ВВЕДЕНИЕ
ГИДРОСТАТИКОЙ называют раздел
гидравлики, в котором изучаются
законы равновесия жидкостей и их
практическое приложение.
При
этом
рассматривается
равновесие жидкости как в неподвижных
(или движущихся равномерно, т.е. без
ускорения) сосудах, так и в сосудах,
движущихся с постоянным ускорением, в
которых жидкость находится в покое
относительно стенок сосуда.

6.

СОСТОЯНИЕ ПОКОЯ ЖИДКОСТИ
Состояние покоя жидкости – это состояние,
при котором её частицы не перемещаются
относительно друг друга и сумма всех сил,
действующих на жидкость, равна нулю.
Покой бывает:
абсолютным
и
относительным .

7.

Первый учебный вопрос
СТАТИКА ЖИДКОСТИ И
ГАЗОВ

8.

9.

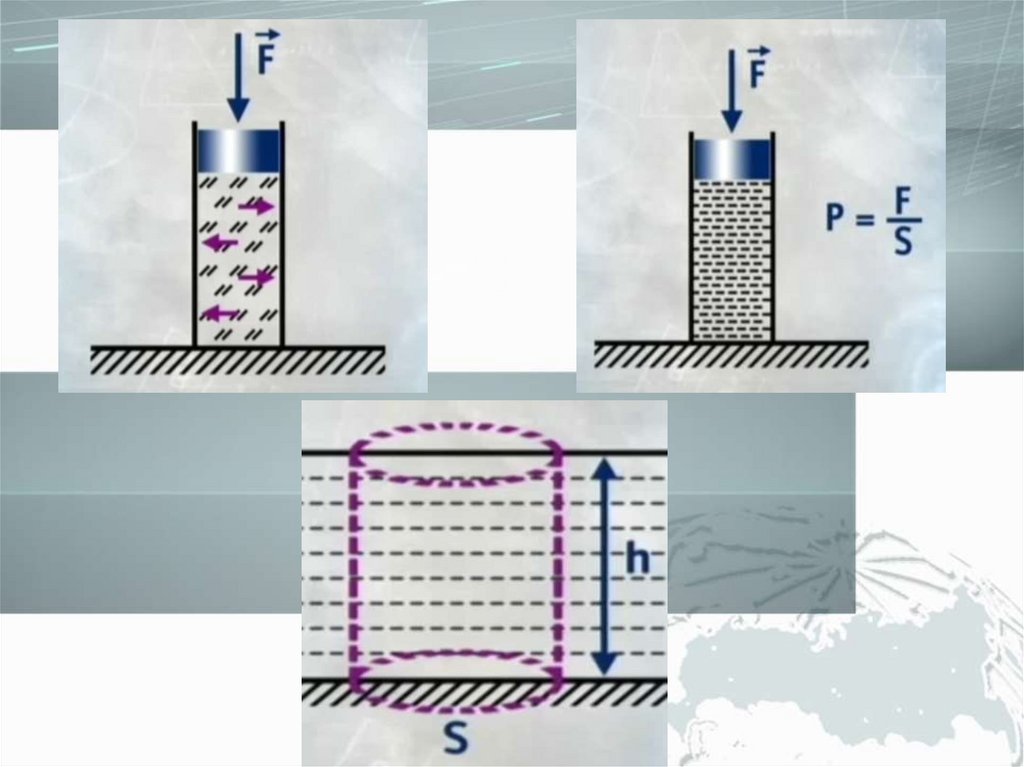
Основные задачи гидростатики :
• определение
гидростатического
давления в любой точке покоящейся
жидкости;
• определение силы давления жидкости
на
плоские
и
криволинейные
поверхности
(стенки
резервуаров,
крышки люков, затворы и т.д.);
• исследование плавучести тел.

10.

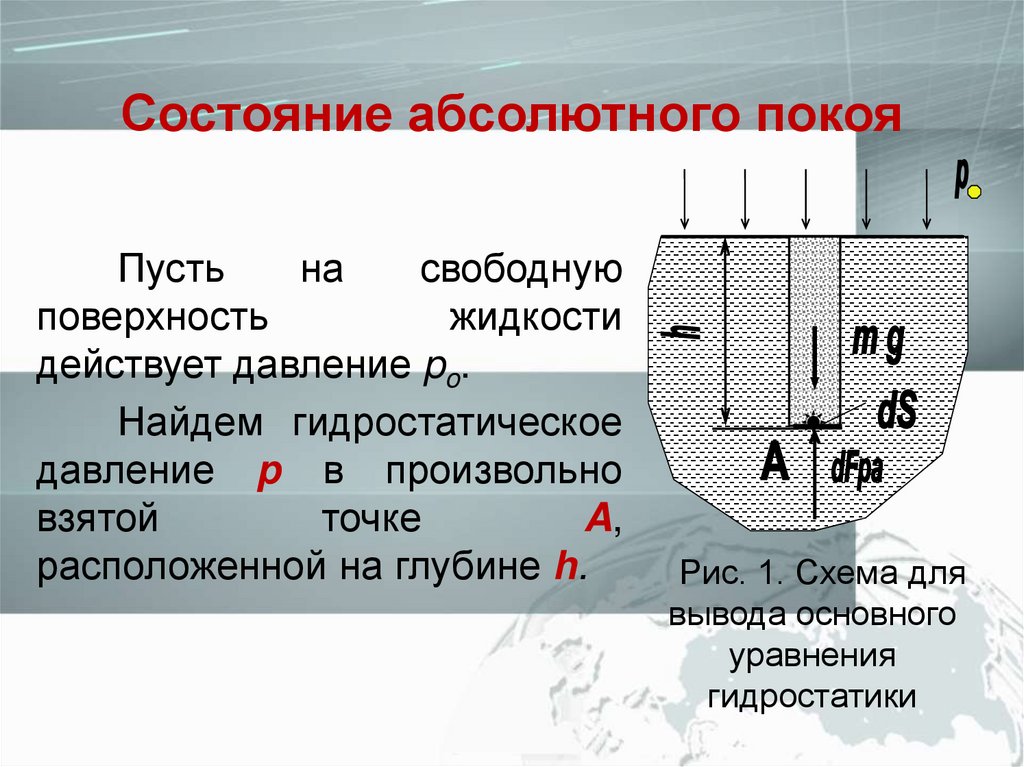
Состояние абсолютного покоя
Пусть
на
свободную
поверхность
жидкости
действует давление po.
Найдем гидростатическое
давление p в произвольно
взятой
точке
A,
расположенной на глубине h.
Рис. 1. Схема для
вывода основного
уравнения
гидростатики

11.

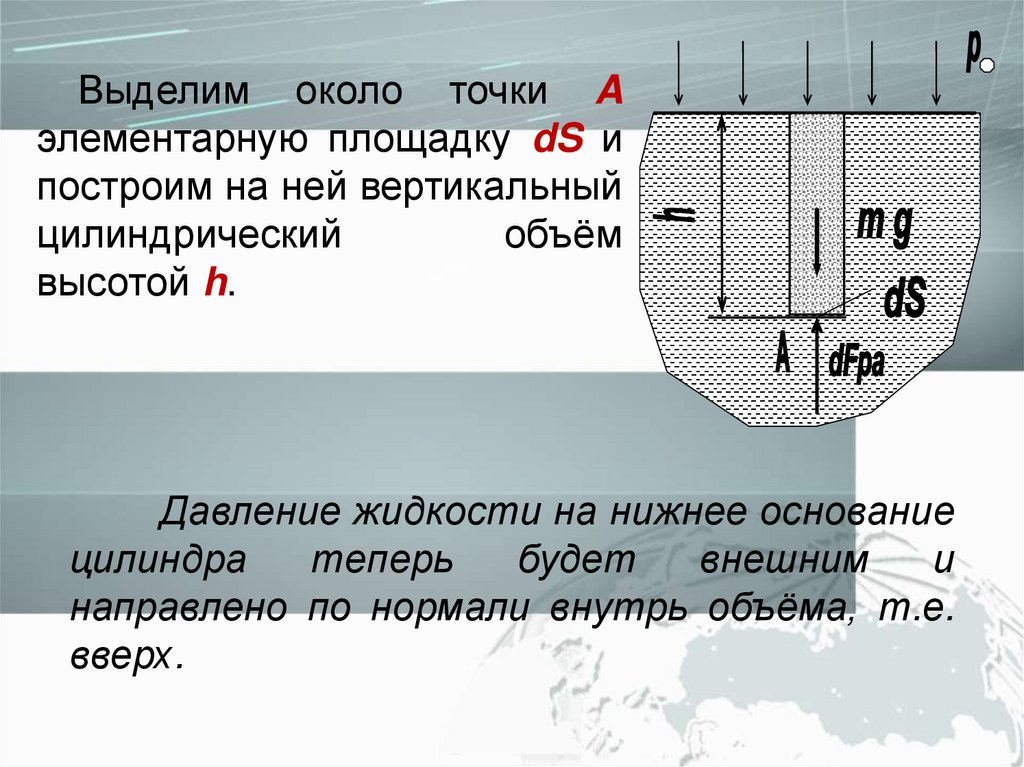
Выделим около точки A
элементарную площадку dS и
построим на ней вертикальный
цилиндрический
объём
высотой h.
Давление жидкости на нижнее основание
цилиндра
теперь
будет
внешним
и
направлено по нормали внутрь объёма, т.е.
вверх.

12.

ОСНОВНОЕ УРАВНЕНИЕ
ГИДРОСТАТИКИ
p po
g h
Давление в любой точке покоящейся
жидкости складывается из двух величин –
давления po на внешней поверхности жидкости
и
давления,
обусловленного
весом
вышележащих слоев жидкости
ρ g h.

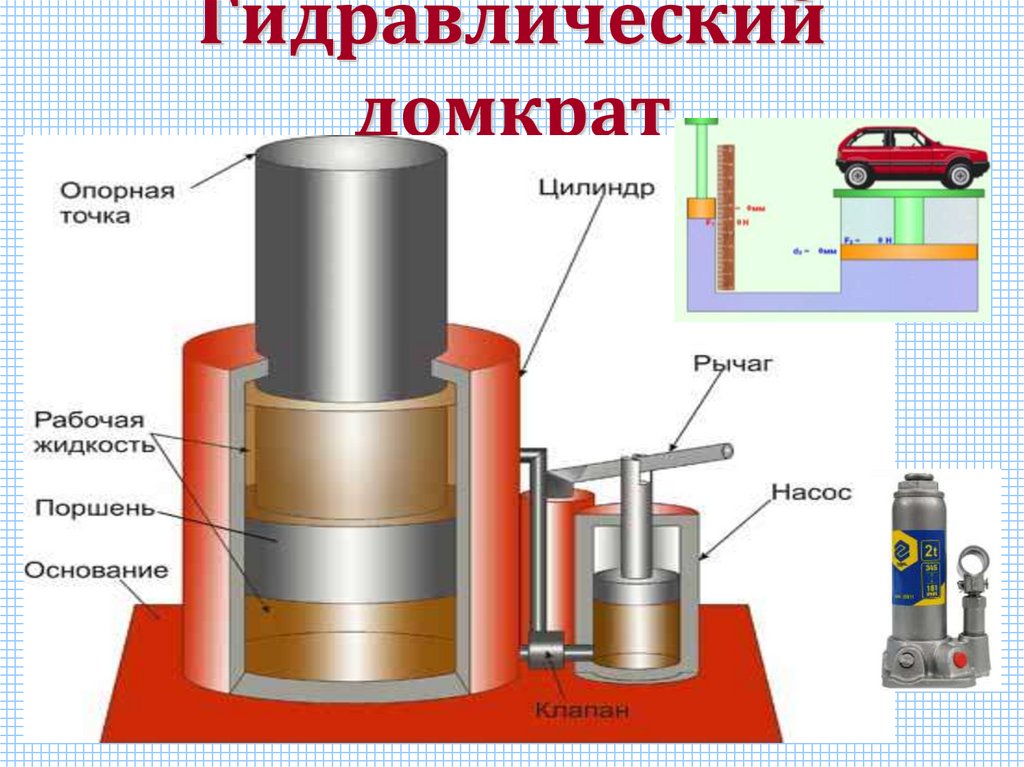
13. Гидравлический домкрат

14. Гидравлический тормоз

1 - тормозные цилиндры передних колес;
2 - трубопровод передних тормозов;
3 - трубопровод задних тормозов;
4 - тормозные цилиндры задних колес;
5 - бачок главного тормозного цилиндра;
6 - главный тормозной цилиндр;
7 - поршень главного тормозного
цилиндра; 8 - шток; 9 - педаль тормоза

15.

Свойства гидростатического давления.
Их три:
1 свойство
Р
Гидростатическое давление направленно по
внутренней нормали к поверхности, граничащей с
жидкостью (рис. 1.5.)
Р0
Р
Р
Рис. 1.5.
К вопросу о свойствах и гидростатического
давления.
Р
Р
Р
Р
Рис. 1.6.
h
Ра
ρgh
Рис. 1.7.
2 свойство
Величина гидростатического давления в любой точке жидкости одинакова по всем
направлениям, т.е. величина давления не зависит от ориентации площадки, на которую она
действует. (Рис.1.6.)
3 свойство.
Гидростатическое давление зависит от глубины, на которой она замеряется (рис.1.7.):
pа=p0+pgh, - основное уравнение гидростатики.
Где pа – гидростатическое давление в точке А на глубине h, Па.
p0 – поверхностное давление;
если сосуд открыт, то p0 = pатм -атмосферное
pgh- избыточное давление (по отношению к поверхностному)
при изменении глубины точки A изменяется слагаемое pgh что и определяет зависимость
ра= f(h).

16.

СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ
ГИДРОСТАТИКИ
Закон Паскаля
Величина po является одинаковой для всех
точек объема жидкости.
Давление, приложенное к внешней
поверхности жидкости , передается всем
точкам этой жидкости и по всем
направлениям одинаково.

17.

Закон паскаля и его техническое приложение.
Внешнее давление, производимое на свободную поверхность покоящейся жидкости,
передаётся одинаково всем её точкам без изменения (следует из анализа уравнения
p=p0+pgh). - Закон используется в различных гидравлических устройствах:
•гидропресс,
•гидродомкрат,
•гидроаккомулятор
Гидропресс – предназначен для создания больших усилий (рис. 1.8.).
F2
1
3
2
4
p1
S1
F2 p
2
S2
Рис. 1.8. Гидропрес
Устройство:
1-поршень первого гидроцилиндра;
2-поршень второго гидроцилиндра;
3-пружина сопротивления (деталь для прессования);
4-рабочая жидкость.
Принцип работы (закон Паскаля):
Под поршнем 1 на поверхности с помощью S1 силой F1
создаётся давление p1=F1/S1
(*)
По закону Паскаля давление p1 передаётся без
изменения под поршень 2
Сила давления под поршнем 2, создаваемая давлением p1:
Из уравнение (*) и (**) следует
F1
F
2
S1
S2
или
F2 p1S2
или
F2 F2
p1 F2 / S2
S2
S1
Из рис.1.8. видно, что S2›S1, следовательно (S1/S2)›1, т.о. усилие F2 на 2-м (большем) поршне возрастает по
отношению к усилию F1 во столько, во сколько площадь S2 больше площади S1.
(**)

18.

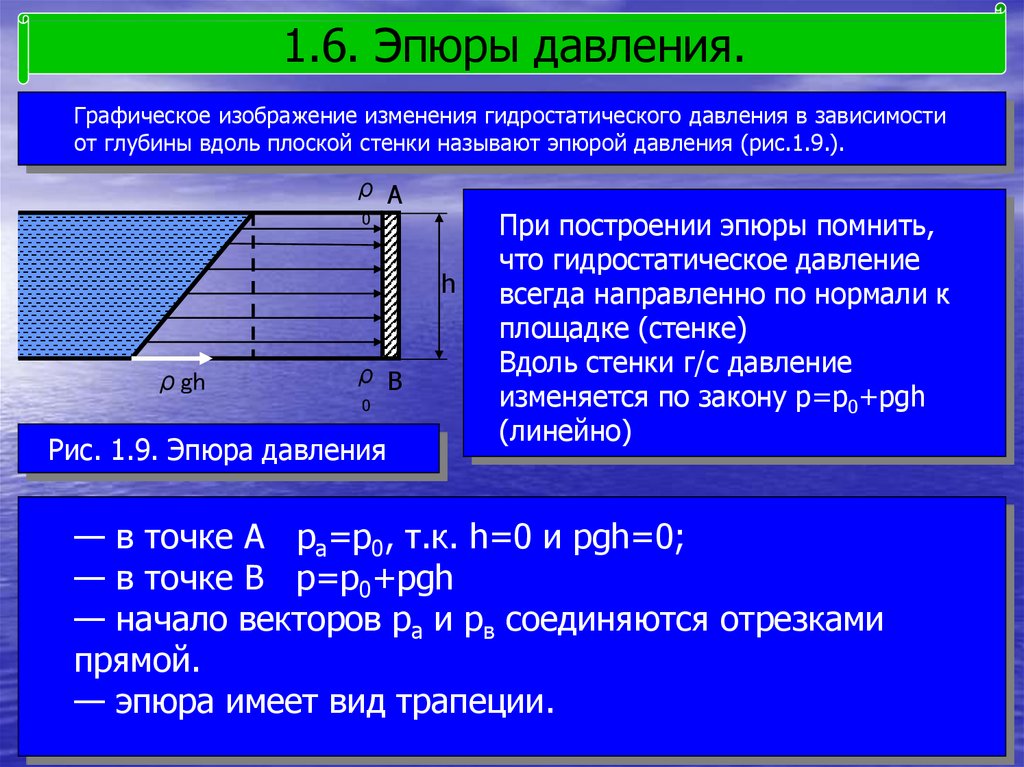
1.6. Эпюры давления.
Графическое изображение изменения гидростатического давления в зависимости
от глубины вдоль плоской стенки называют эпюрой давления (рис.1.9.).
ρА
0
h
ρgh
ρВ
0
Рис. 1.9. Эпюра давления
При построении эпюры помнить,
что гидростатическое давление
всегда направленно по нормали к
площадке (стенке)
Вдоль стенки г/с давление
изменяется по закону p=p0+pgh
(линейно)
— в точке А pа=p0, т.к. h=0 и pgh=0;
— в точке В p=p0+pgh
— начало векторов pа и pв соединяются отрезками
прямой.
— эпюра имеет вид трапеции.

19.

ГИДРОСТАТИЧЕСКИЙ
ПАРАДОКС
давление жидкости на днище не
зависит от формы сосуда (веса
жидкости в сосуде)

20.

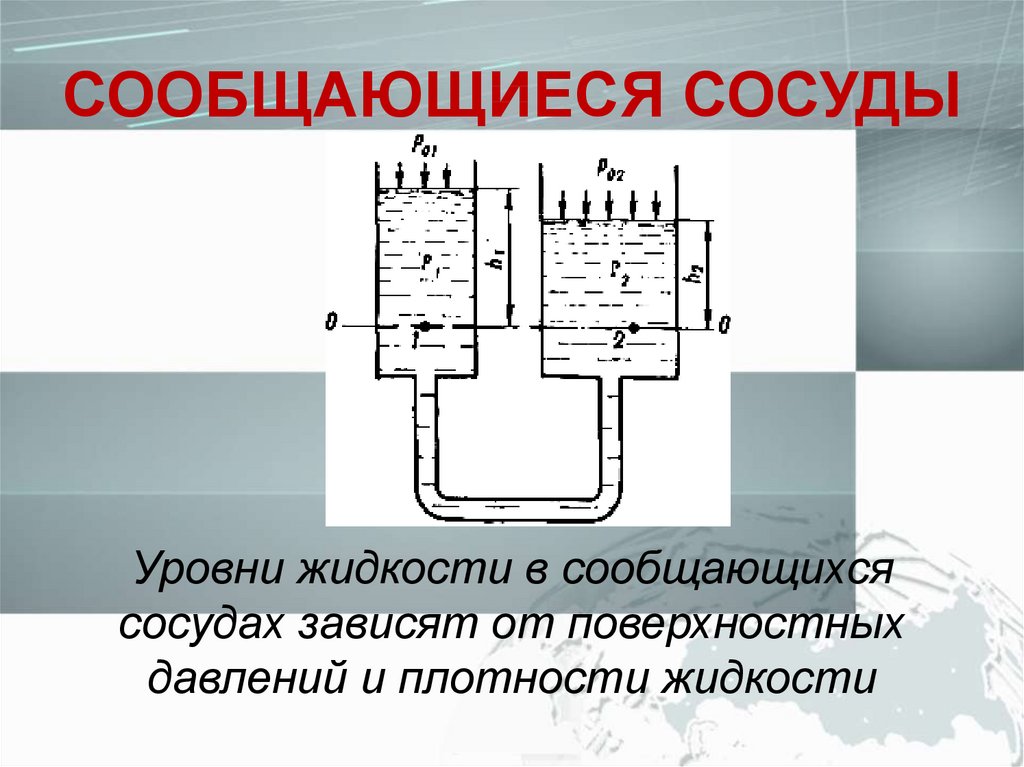
СООБЩАЮЩИЕСЯ СОСУДЫ
Уровни жидкости в сообщающихся
сосудах зависят от поверхностных
давлений и плотности жидкости

21.

ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ
Под относительным покоем понимается
такое равновесие жидкости, при котором нет
движения ее частей относительно друг друга и
по отношению к стенкам сосуда, но сам сосуд
ускоренно движется относительно Земли.
В состояние относительного покоя жидкость
может прийти, если сосуд в котором она
находится движется:
а) прямолинейно равноускорено;
б) равномерно вращательно.

22.

а)
б)
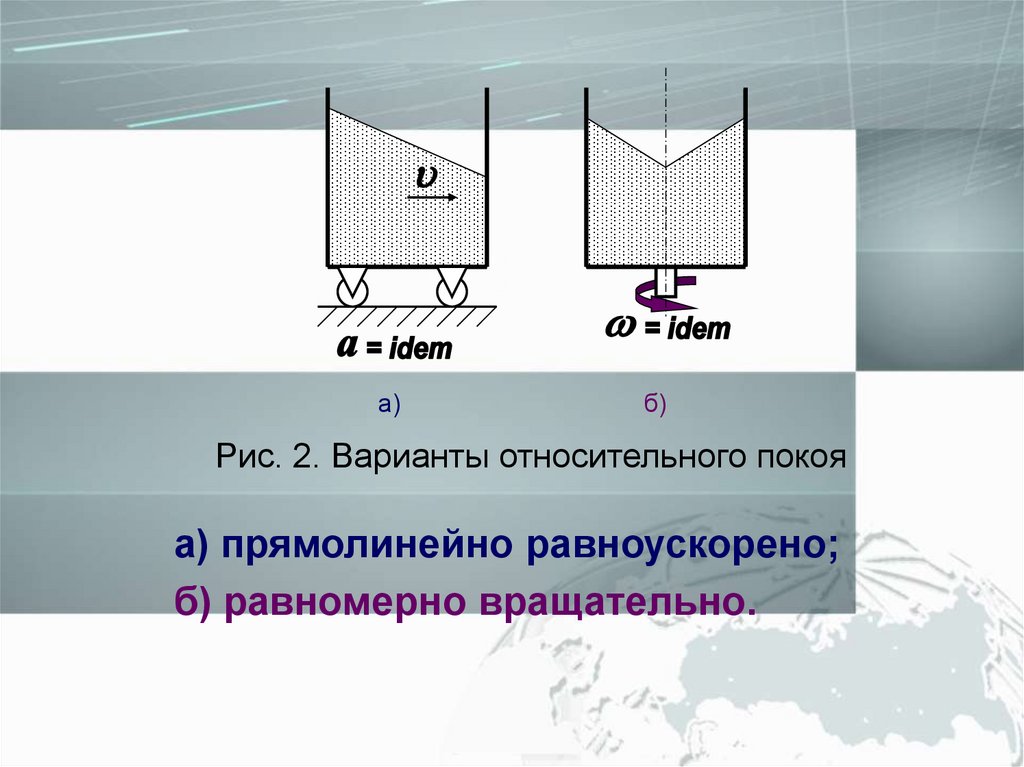
Рис. 2. Варианты относительного покоя
а) прямолинейно равноускорено;
б) равномерно вращательно.

23.

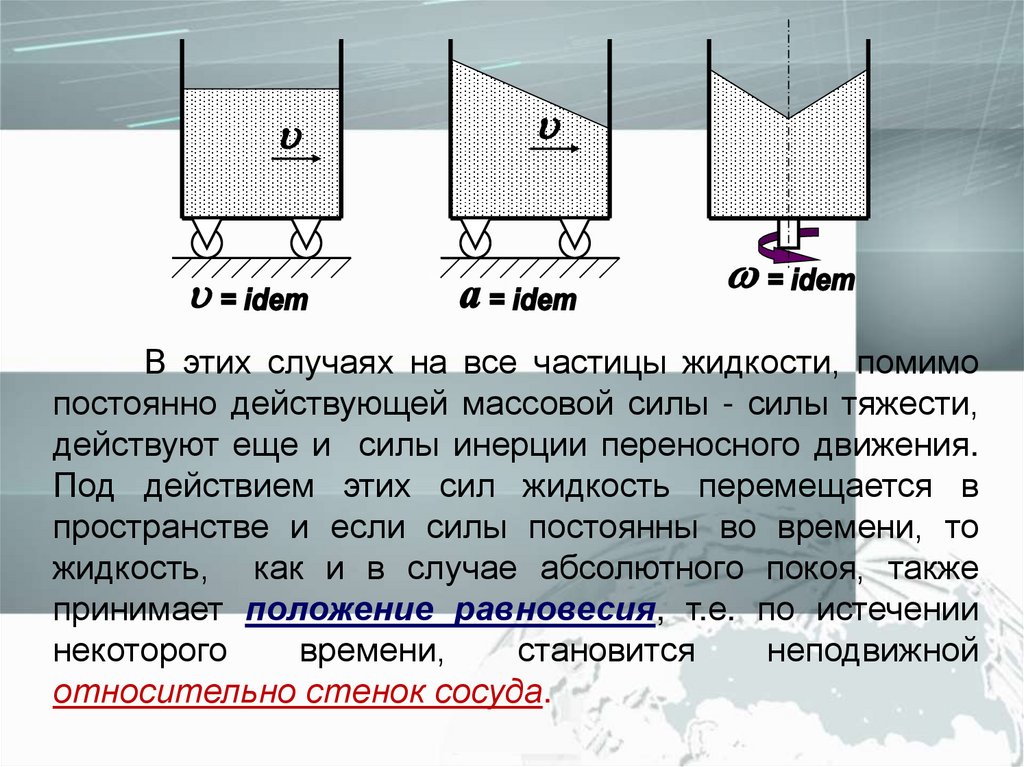
В этих случаях на все частицы жидкости, помимо
постоянно действующей массовой силы - силы тяжести,
действуют еще и силы инерции переносного движения.
Под действием этих сил жидкость перемещается в
пространстве и если силы постоянны во времени, то
жидкость, как и в случае абсолютного покоя, также
принимает положение равновесия, т.е. по истечении
некоторого
времени,
становится
неподвижной
относительно стенок сосуда.

24.

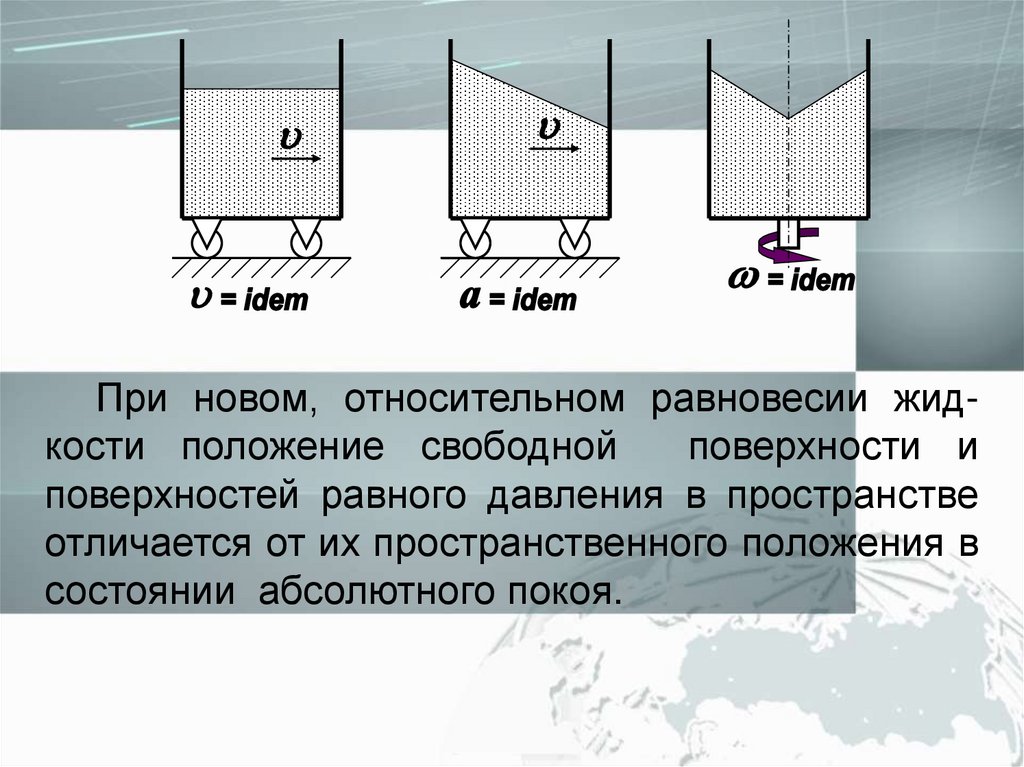
При новом, относительном равновесии жидкости положение свободной
поверхности и
поверхностей равного давления в пространстве
отличается от их пространственного положения в
состоянии абсолютного покоя.

25.

Свойства
поверхностей
уровня заключаются в том, что
они не пересекаются друг с
другом
и
располагаются
перпендикулярно к суммарному
вектору массовых сил.

26.

В сосуде, движущемся горизонтально и
равноускорено, поверхности уровня будут иметь
наклон,
угол
которого
определится
соотношением горизонтального ускорения и
ускорения свободного падения.

27.

Частные случаи относительного покоя
жидкости
Fи
G
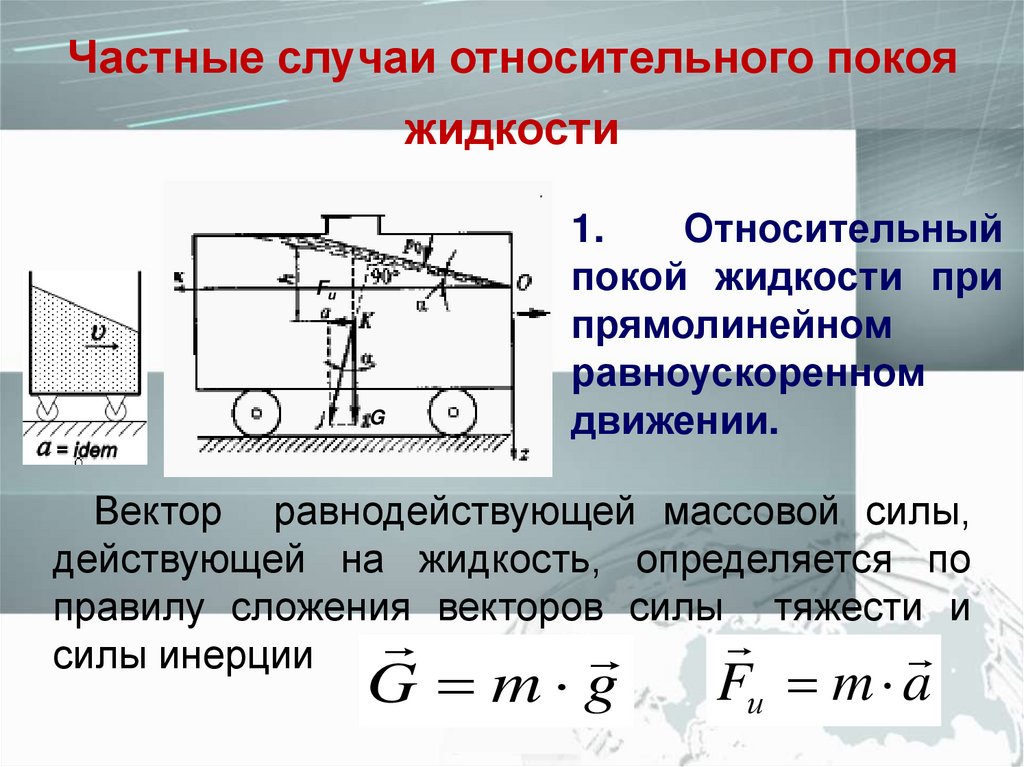
1.
Относительный
покой жидкости при
прямолинейном
равноускоренном
движении.
Вектор равнодействующей массовой силы,
действующей на жидкость, определяется по
правилу сложения векторов силы тяжести и
силы инерции
G m g
Fи m a

28.

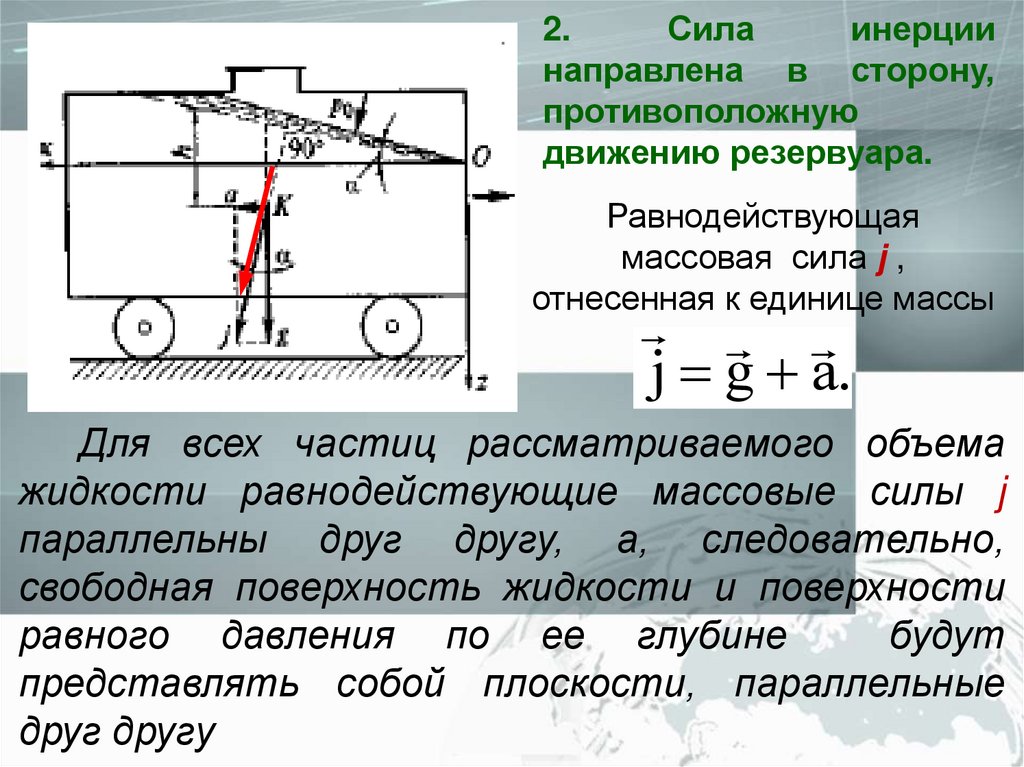
2.
Сила
инерции
направлена в сторону,
противоположную
движению резервуара.
Равнодействующая
массовая сила j ,
отнесенная к единице массы
j g a.
Для всех частиц рассматриваемого объема
жидкости равнодействующие массовые силы j
параллельны друг другу, а, следовательно,
свободная поверхность жидкости и поверхности
равного давления по ее глубине
будут
представлять собой плоскости, параллельные
друг другу

29.

ВЫВОДЫ
1. По основному уравнению гидростатики можно
определить давление в любой точке покоящейся жидкости,
которое складывается из двух величин - давления на
внешней поверхности жидкости и давления, обусловленного
весом вышележащих слоев жидкости.
2. Величина pо является одинаковой для всех точек
объёма
жидкости,
поэтому,
учитывая
свойство
гидростатического давления, можно сказать, что
Давление, приложенное к внешней поверхности
жидкости, передается всем точкам этой жидкости и
по всем направлениям одинаково.
Это положение известно под названием
Закона Паскаля.

30.

Второй учебный вопрос
СТАТИКА ТЕЛА,
ПОГРУЖЕННОГО В
ЖИДКОСТЬ

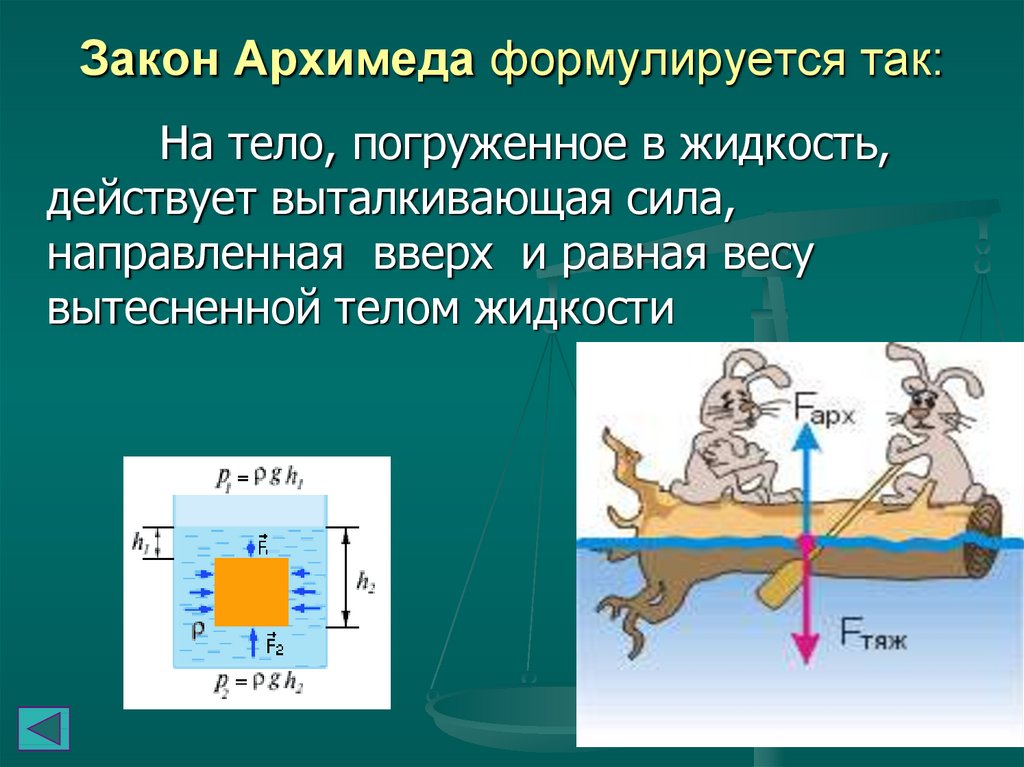
31. Закон Архимеда формулируется так:

На тело, погруженное в жидкость,
действует выталкивающая сила,
направленная вверх и равная весу
вытесненной телом жидкости

32.

33. Сила Архимеда

34. В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S

Разность давлений на нижнюю и
верхнюю грани есть:
Δp = p2 – p1 = ρgh.
Поэтому выталкивающая сила будет
направлена вверх, и ее модуль равен
FA = F2 – F1 = SΔp = ρgSh = ρgV,
где V – объем вытесненной телом
жидкости, а ρV – ее масса

35. Сила Архимеда

FВытал кив ающая
F2 F1
Причина
возникновения
выталкивающей
силы в разности сил
на разных глубинах

36.

На тело, погруженное в
жидкость или газ, действует
выталкивающая …………….
сила, …равная
FАрхимеда= ρж gV
…весу жидкости или газа, .
вытесненного
этим……. Телом!!!!!

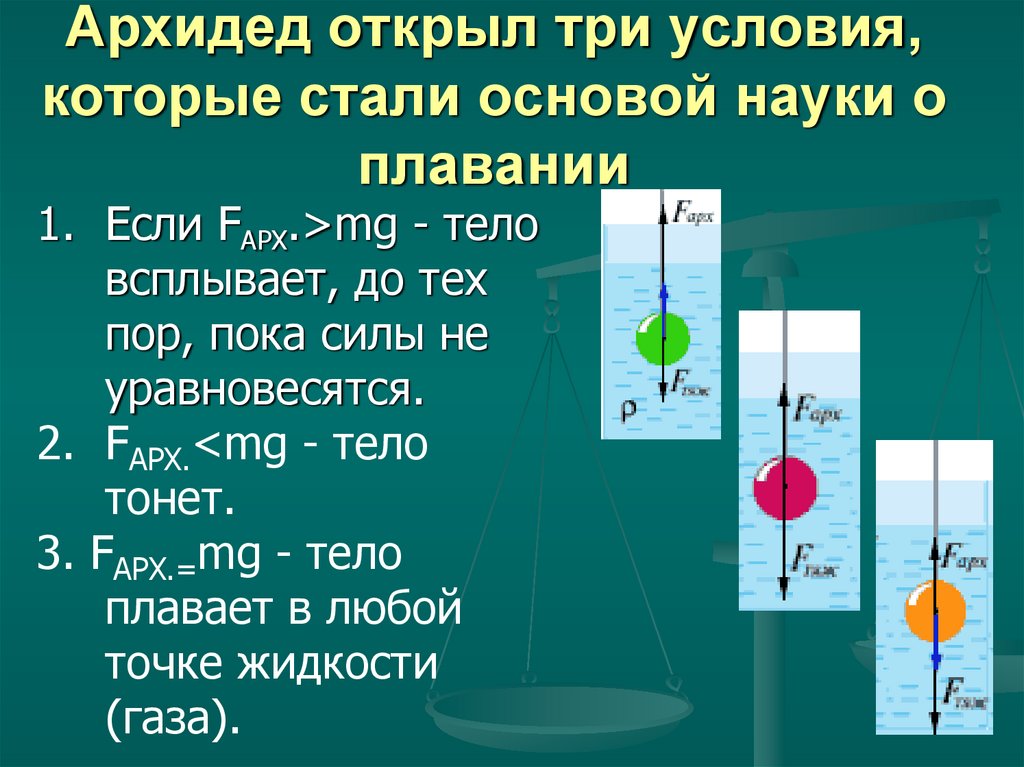
37. Архидед открыл три условия, которые стали основой науки о плавании

1. Если FАРХ.>mg - тело
всплывает, до тех
пор, пока силы не
уравновесятся.
2. FАРХ.<mg - тело
тонет.
3. FАРХ.=mg - тело
плавает в любой
точке жидкости
(газа).

38. Сила Архимеда равна произведению плотности жидкости на коэффициент g и на объем тела

39. Условие плавания тел

Если плотность тела больше плотности
жидкости, то тело в ней тонет.
Если плотность тела меньше плотности
жидкости, то тело в ней всплывает.
При равенстве плотностей тела и
жидкости, тело плавает.

40.

Надводная часть айсберга имеет объем ΔV
= 500 м3.
Найти объем айсберга V, если плотность
льда ρльда = 0,92 г/см3, а плотность воды
ρводы = 1,03 г/см3.

41. Решение:

Условие равновесия айсберга:
FАрхимеда = Mg
ρvg ∙ (V – ΔV) = ρльдаgV.
Откуда:
v V
V
в оды л ьда

42.

ЗАКЛЮЧЕНИЕ
В данной лекции мы ознакомились с
основными законами Гидростатики.
Для закрепления пройденного материала
рекомендуется на самоподготовке ответить на
следующие вопросы по пройденному материалу:

43.

1. Что изучает «Гидростатика».
2. Основное уравнение гидростатики.
3. Следствия из основного закона гидростатики.
4. Сущность закона Паскаля.
5. Виды покоя жидкости.
6. Что такое поверхность уровня.
7. Как направлены поверхности уровня.
8. Сущность закона Архимеда.
9. Каково условие плавания тел.

44.

Задание на самоподготовку:
Е.А. Дундур Основы машиностроительной
гидравлики. -Пермь., 1998 г., с.12-22.