Similar presentations:
Элементы симметрии в правильных многогранниках
1. Элементы симметрии в правильных многогранниках.
ЭЛЕМЕНТЫ СИММЕТРИИ ВПРАВИЛЬНЫХ МНОГОГРАННИКАХ.
2.
многогранник называетсяправильным, если все его грани равные друг другу правильные
многоугольники, а все его
двугранные углы равны между
собой. Мы знаем, что существует
правильный многоугольник с
любым количеством сторон, т.е.
число видов правильных
многоугольников - бесконечно.
Однако для правильных
многогранников это не так. Еще
Евклид доказал, что существует
всего пять видов правильных
многогранников.
Перечислим правильные
многогранники:
- правильные тетраэдры
(четырехгранники), у которых
грани правильные треугольники
- кубы (правильные гексаэдры,
шестигранники), у которых грани квадраты
- правильные октаэдры
(восьмигранники), у которых
грани - правильные треугольники
- правильные додекаэдры
(двенадцатигранники), у которых
грани - правильные
пятиугольники
- правильные икосаэдры
(двадцатигранники), у которых
грани - правильные треугольники
3.
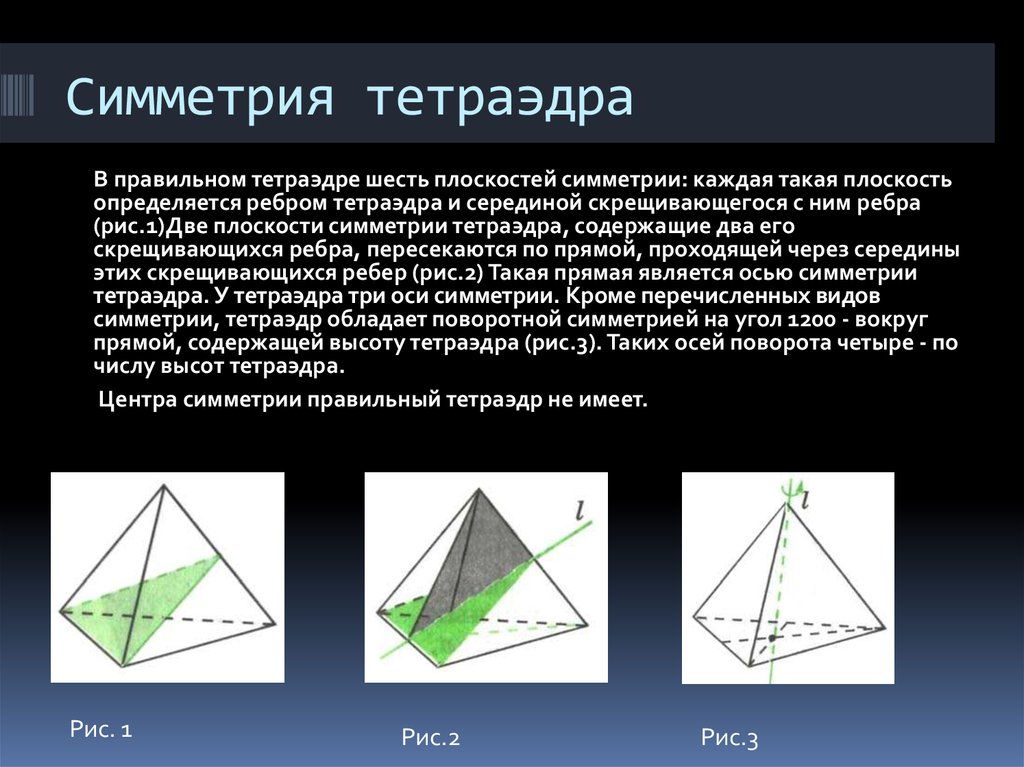
4. Симметрия тетраэдра
В правильном тетраэдре шесть плоскостей симметрии: каждая такая плоскостьопределяется ребром тетраэдра и серединой скрещивающегося с ним ребра
(рис.1)Две плоскости симметрии тетраэдра, содержащие два его
скрещивающихся ребра, пересекаются по прямой, проходящей через середины
этих скрещивающихся ребер (рис.2) Такая прямая является осью симметрии
тетраэдра. У тетраэдра три оси симметрии. Кроме перечисленных видов
симметрии, тетраэдр обладает поворотной симметрией на угол 1200 - вокруг
прямой, содержащей высоту тетраэдра (рис.3). Таких осей поворота четыре - по
числу высот тетраэдра.
Центра симметрии правильный тетраэдр не имеет.
Рис. 1
Рис.2
Рис.3
5. Симметрия куба
Куб (как и произвольный параллелепипед) имеет центр симметрии точку пересечения диагоналей. Оси симметрии куба изображены нарисунке 3. Те его оси симметрии куба, которые проходят через центры
его противоположных граней, являются и осями его поворотной
симметрии на угол 90 . Оказывается, куб имеет и другие оси поворота.
Прямая, содержащая диагональ куба, является осью поворотной
симметрии куба на угол 120. Таких осей в кубе четыре.
6. Плоскости симметрии куба изображены на рисунке
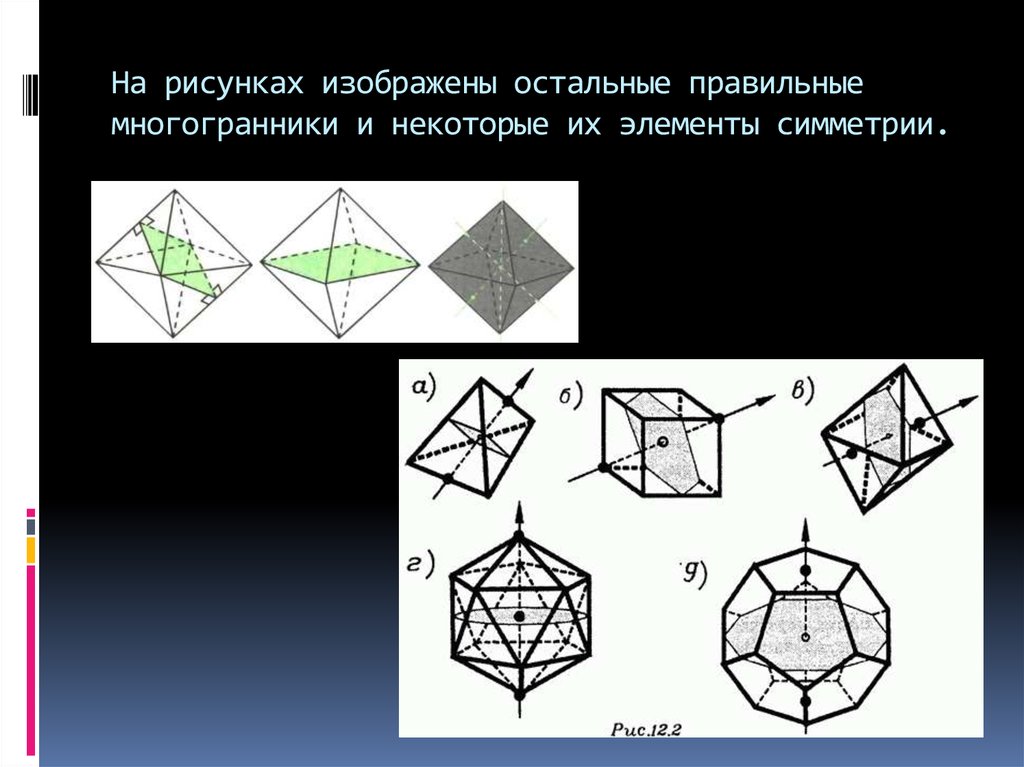
7. На рисунках изображены остальные правильные многогранники и некоторые их элементы симметрии.
8.
Оси зеркальной поворотной симметрии в икосаэдре (так же, как и в кубе)соединяют противоположные вершины этого многогранника (рис. 1)
1 рис
2 рис
3 рис
а в додекаэдре (как и в октаэдре) эти оси идут через центры их параллельных
граней (рис. 2). Плоскости, проходящие через центры симметрии правильных
многогранников и перпендикулярные указанным осям,
пересекают правильные многогранники по правильным многоугольникам(рис.3).
В частности, додекаэдр и икосаэдр они пересекают по правильным
десятиугольникам (рис. 12.23 г,д). Из сказанного следует, что икосаэдр и додекаэдр
самосовмещаются зеркальными поворотами относительно осей шестого и
десятого порядков.






 mathematics
mathematics








