Круг. Окружность. Длина окружности. Площадь круга

1. Круг. Окружность. Длина окружности. Площадь круга.

Подготовила: Деревянко София

2. Круг. Окружность. Длина окружности. Площадь круга.

O Окружность – множество всех точек на
плоскости, равноудаленных от данной
точки.

3. Хор­дой на­зы­ва­ет­ся такой от­ре­зок, ко­то­рые со­еди­ня­ет любые две точки, ле­жа­щие на окруж­но­сти. Диа­метр – это такая

Хордой называется такой отрезок, которые соединяет
любые две точки, лежащие на окружности.
Диаметр – это такая хорда, которая проходит через центр
окружности. Соответственно, как следствие, нетрудно догадаться, что диаметр равен двум радиусам.
O D=2r

4. Круг – это все точки на плос­ко­сти, ко­то­рые лежат внут­ри окруж­но­сти, а также сама окруж­ность

Круг – это все точки на плоскости, которые лежат внутри
окружности, а также сама окружность

5.

6. Один из спо­со­бов, ко­то­рый был пред­ло­жен, таков: возь­мем, на­при­мер, ста­кан, у ко­то­ро­го дно будет круг­лой формы, и

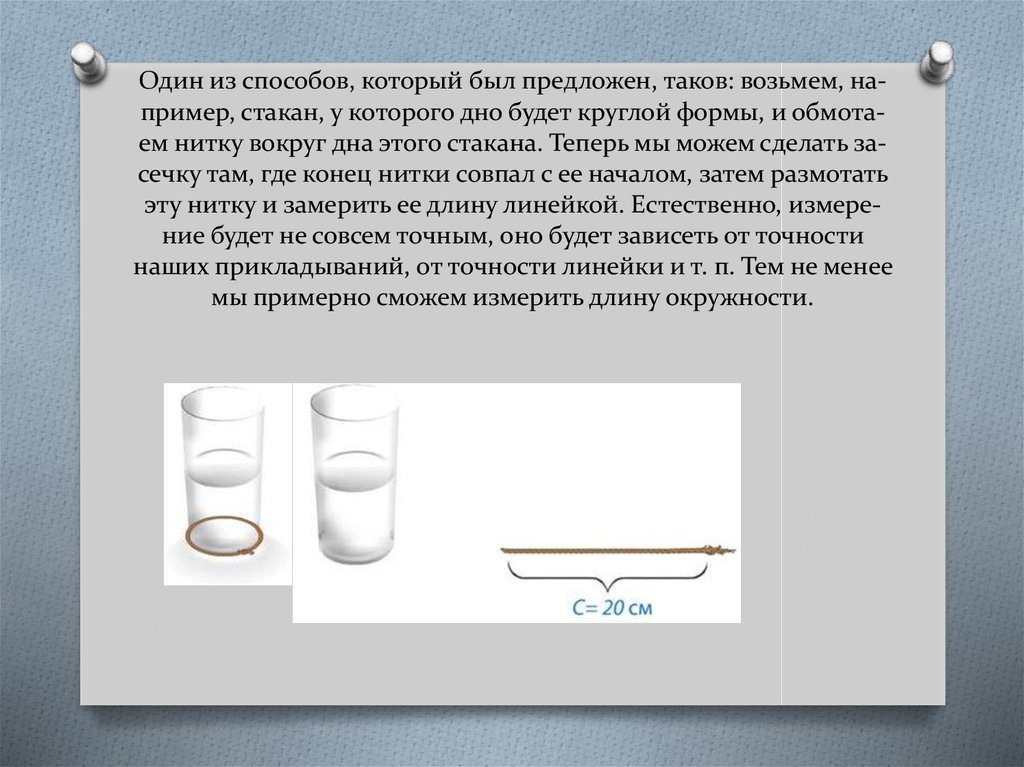
Один из способов, который был предложен, таков: возьмем, например, стакан, у которого дно будет круглой формы, и обмотаем нитку вокруг дна этого стакана. Теперь мы можем сделать засечку там, где конец нитки совпал с ее началом, затем размотать
эту нитку и замерить ее длину линейкой. Естественно, измерение будет не совсем точным, оно будет зависеть от точности
наших прикладываний, от точности линейки и т. п. Тем не менее
мы примерно сможем измерить длину окружности.

7. Еще в древ­но­сти люди за­ме­ти­ли, что если вы уве­ли­чи­те ра­ди­ус окруж­но­сти, на­при­мер в два раза, то и длина этой

Еще в древности люди заметили, что если вы увеличите
радиус окружности, например в два раза, то и длина этой
окружности увеличится в два раза. Если уменьшить радиус в три раза, то и длина уменьшится в три раза. Иначе говоря: длина окружности и ее радиус пропорциональны
друг другу. То есть их отношение – это постоянное число.

8. Итак, пусть длина окруж­но­сти , а диа­метр окруж­но­сти – . Так как от­но­ше­ние длины к диа­мет­ру все­гда по­сто­ян­ное, то

Итак, пусть длина окружности , а диаметр окружности – . Так как
отношение длины к диаметру всегда постоянное, то его можно
примерно посчитать. Проделав это, вы примерно получите
число Так как число, которое равно отношению длины окружности к ее диаметру, не могли посчитать точно, его обозначили
специальной буквой, буквой п (буква греческого алфавита).

9. Рас­смот­рим круг, за­ме­тим, что пло­щадь этого круга, мень­ше, чем пло­щадь квад­ра­та, ко­то­рый опи­сы­ва­ет этот круг.

Рассмотрим круг, заметим, что площадь этого круга, меньше,
чем площадь квадрата, который описывает этот круг. Причем
площадь этого квадрата мы легко можем посчитать – это квадрат
его стороны.
С другой стороны, мы можем немного приблизить нашу фигуру
к кругу, если вырезать квадратные уголки со сторон вершин
квадрата. Остается фигура, которая по площади ближе к кругу.
Аналогичным образом мы можем продолжать до бесконечности.

10. Спасибо за внимание!