Приближенное вычисление интегралов

1. Приближенное вычисление интегралов

2.

Пусть требуется вычислить
a∫
b
f(x)dx ,
где f(x) заданная функция,
непрерывная на [a;b], то
a∫
b
f(x)dx = F(b) - F(a)

3.

Если первообразная функция F(x) не
может быть найдена;
если функция y=f(x) задана
графически;
если функция y=f(x) задана таблицей,
то применяют приближенные формулы

4.

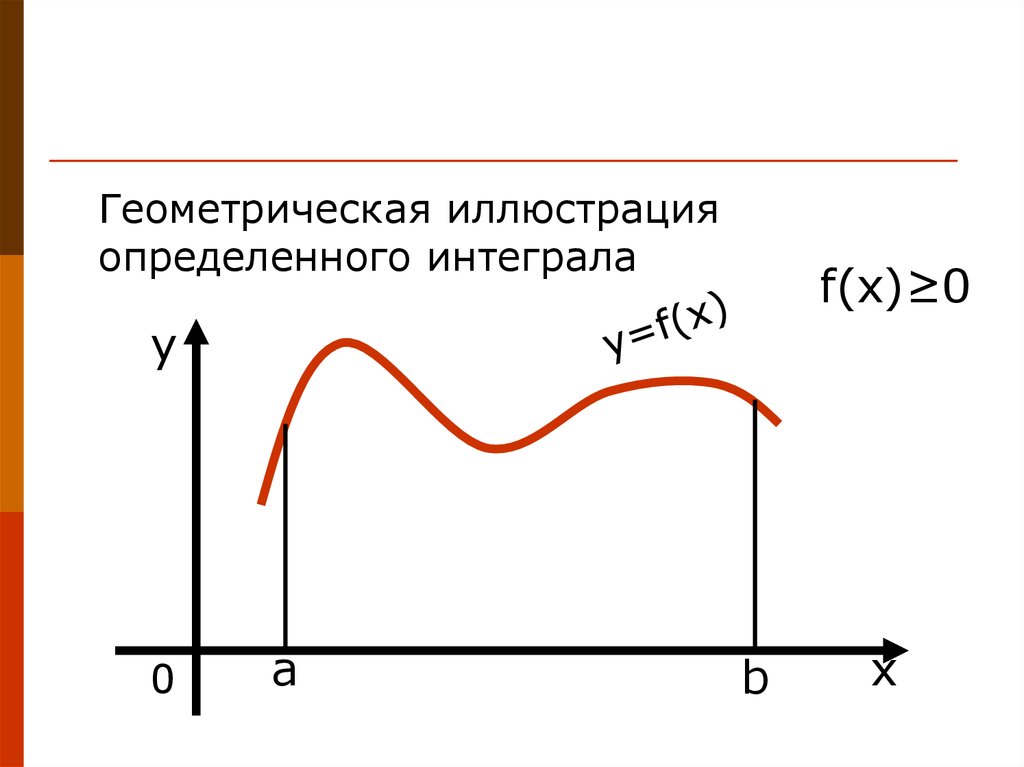
Геометрическая иллюстрация
определенного интеграла
f(x)≥0
y
0
a
b
x

5. Формула прямоугольников

Пусть требуется вычислить
определенный интеграл
a∫
причем
b
f(x)dx ,
f(x)≥0
на [a;b]

6. Формула прямоугольников

y
y0
y1
a =x0 x1
Xi+1-xi=h
yN
x
xN-1
2
h=(b-a)/n
b =xN x

7. Формула прямоугольников

Каждая частичная криволинейная
трапеция заменяется прямоугольником.
Основание h, высоты – y0, y1, … yN-1.
Если n достаточно велико, то
b
a∫
f(x)dx≈(b-a)/n*(y0+y1+…+yN-1)
Формула прямоугольников с левыми
ординатами

8. Формула прямоугольников

y
y0
y1
a =x0 x1
Xi+1-xi=h
yN
x
xN-1
2
h=(b-a)/n
b =xN x

9. Формула прямоугольников

b
∫
f(x)dx≈(b-a)/n*(y
+y2+…+yN)
1
a
Формула прямоугольников с правыми
ординатами