Возведение в степень. 7 класс

1.

2.

Дорогие ребята!
Сегодня я предлагаю вам закрепить умение
возводить числа в степень.
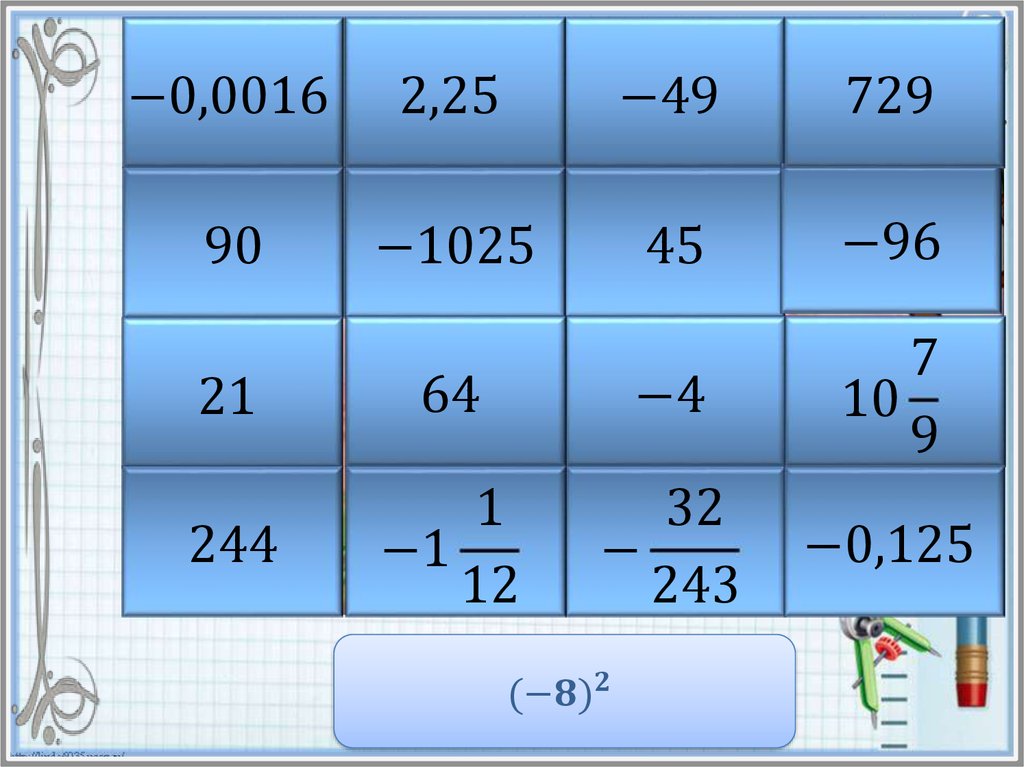
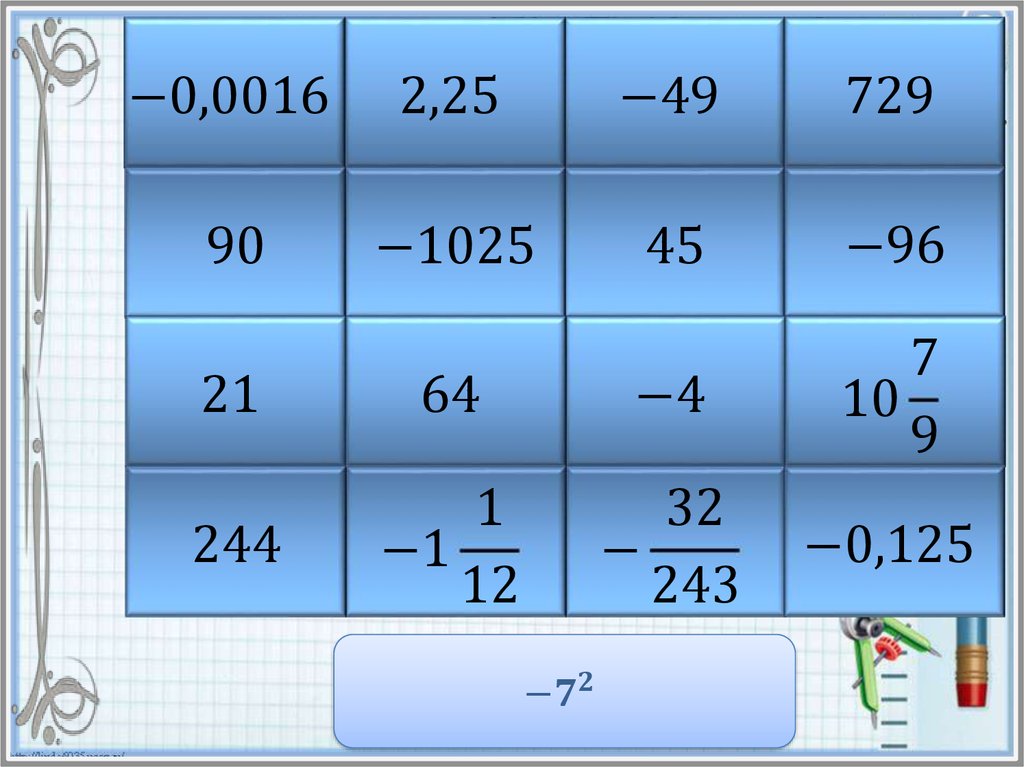
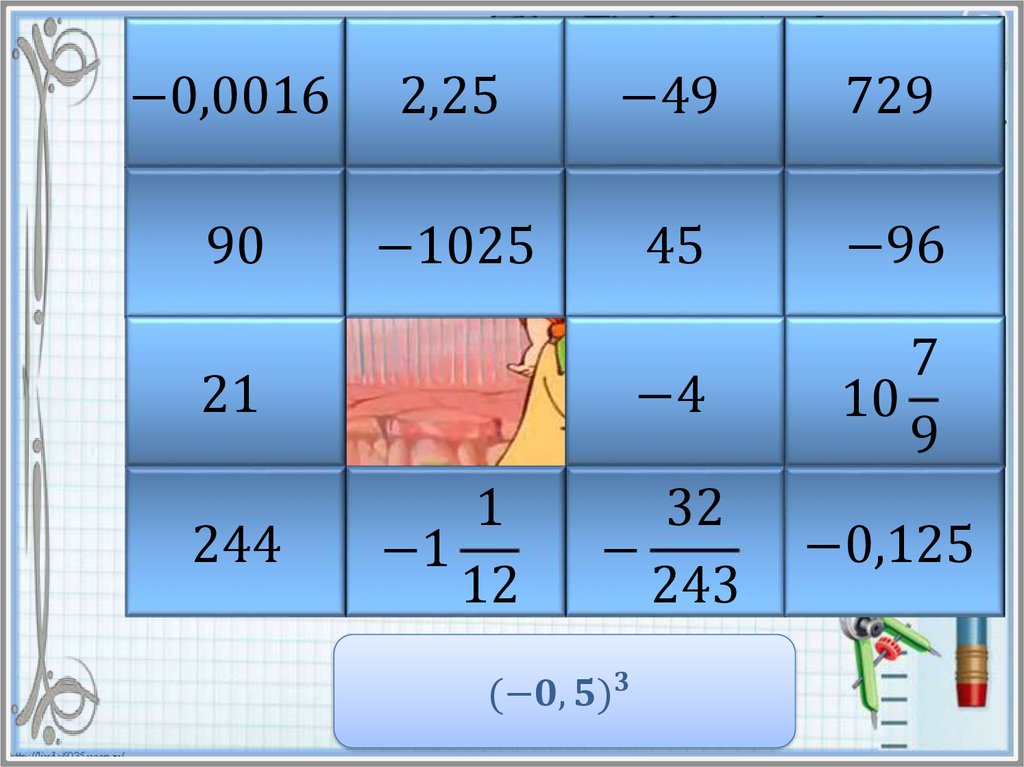
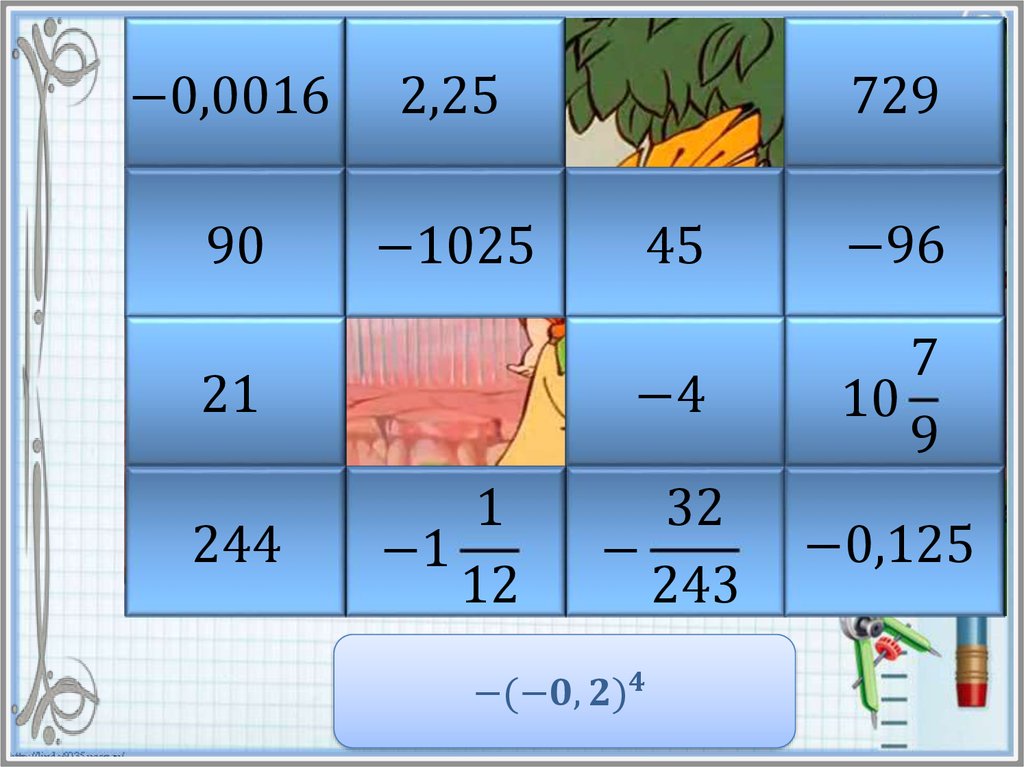
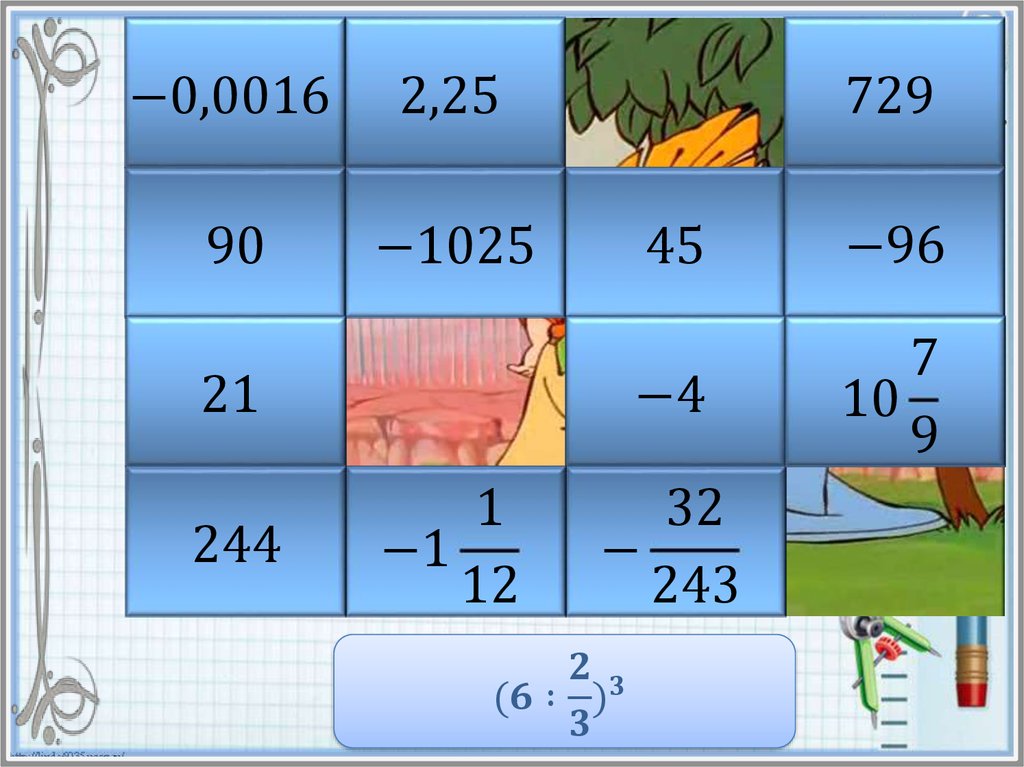
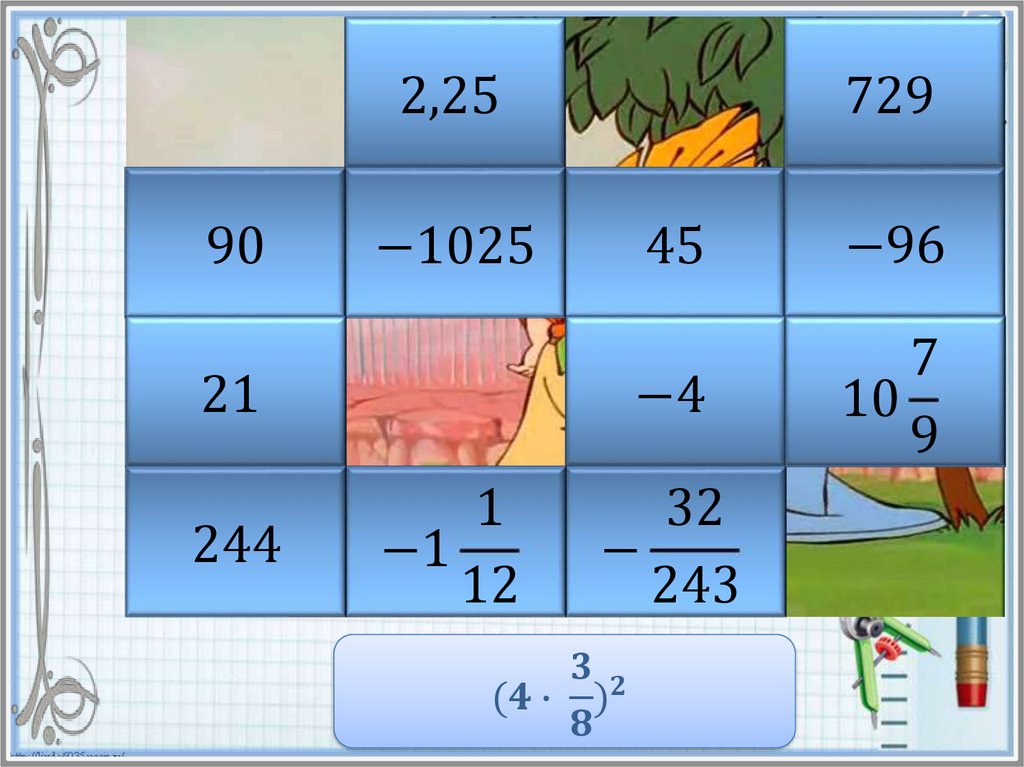
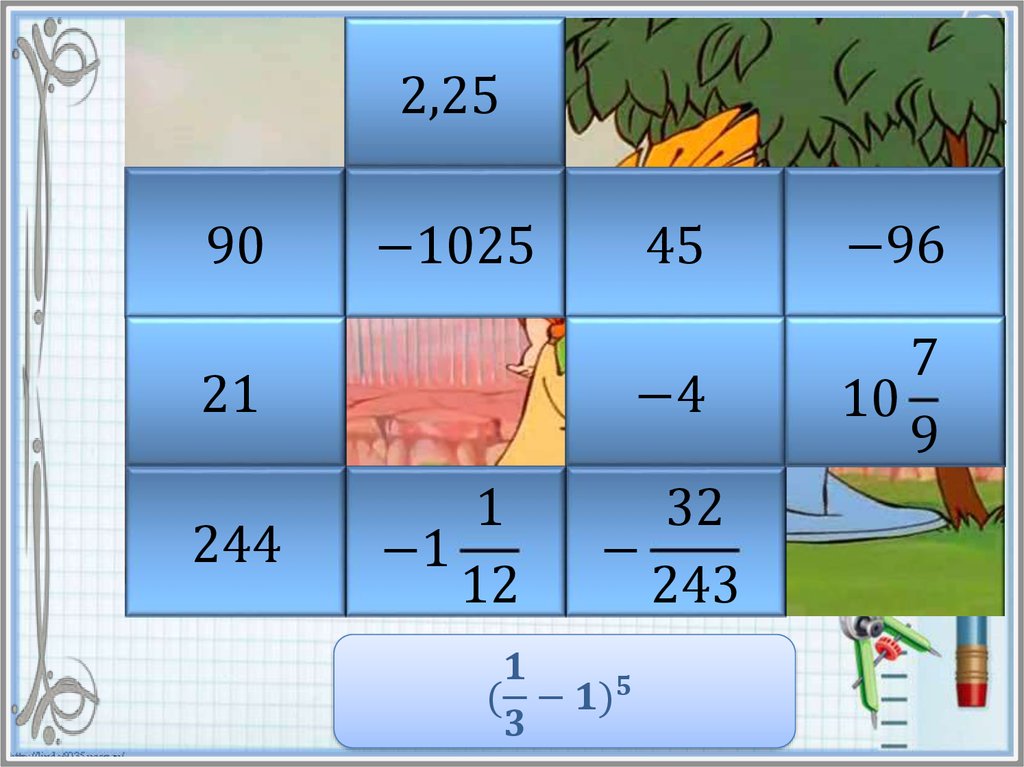
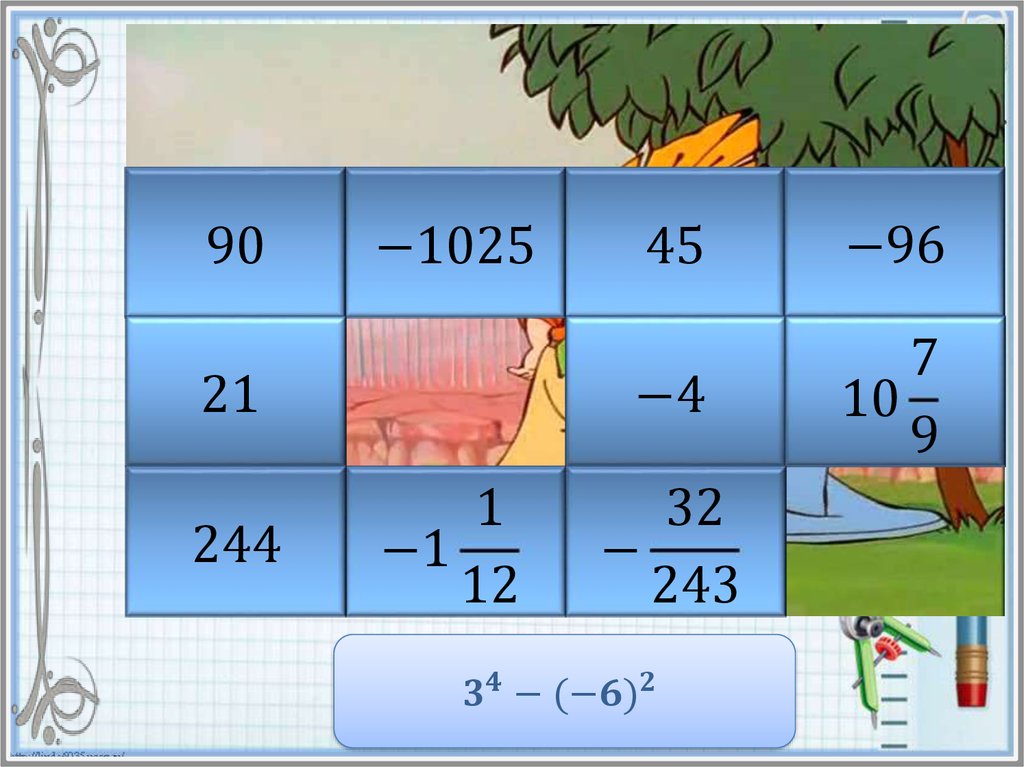
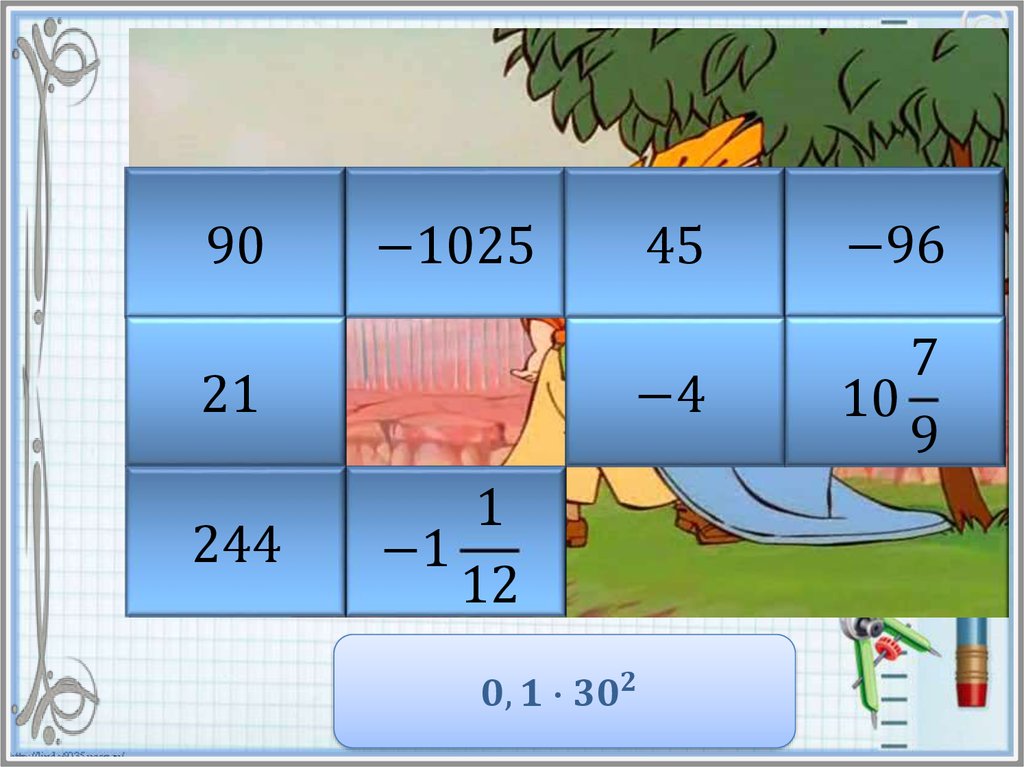
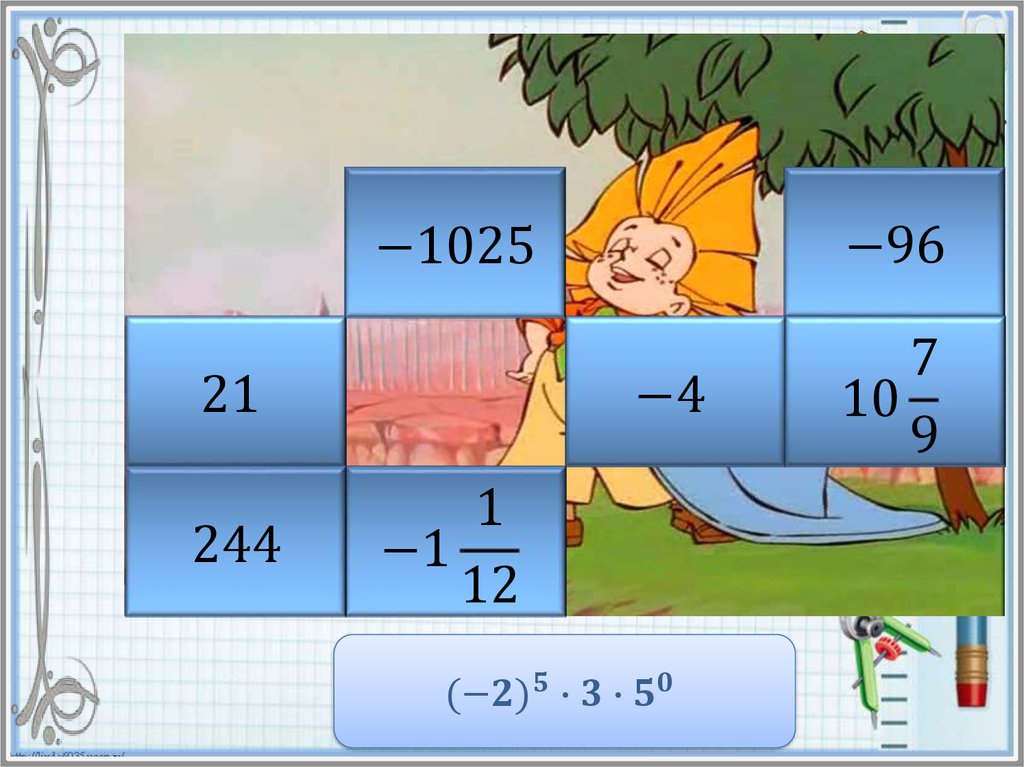
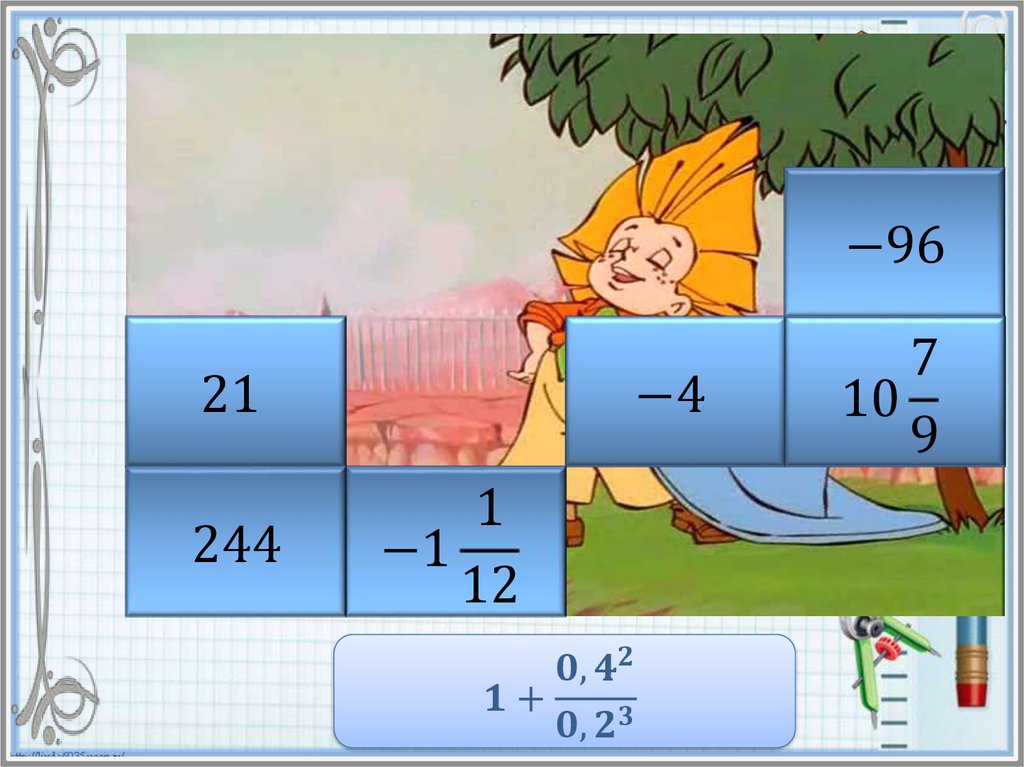
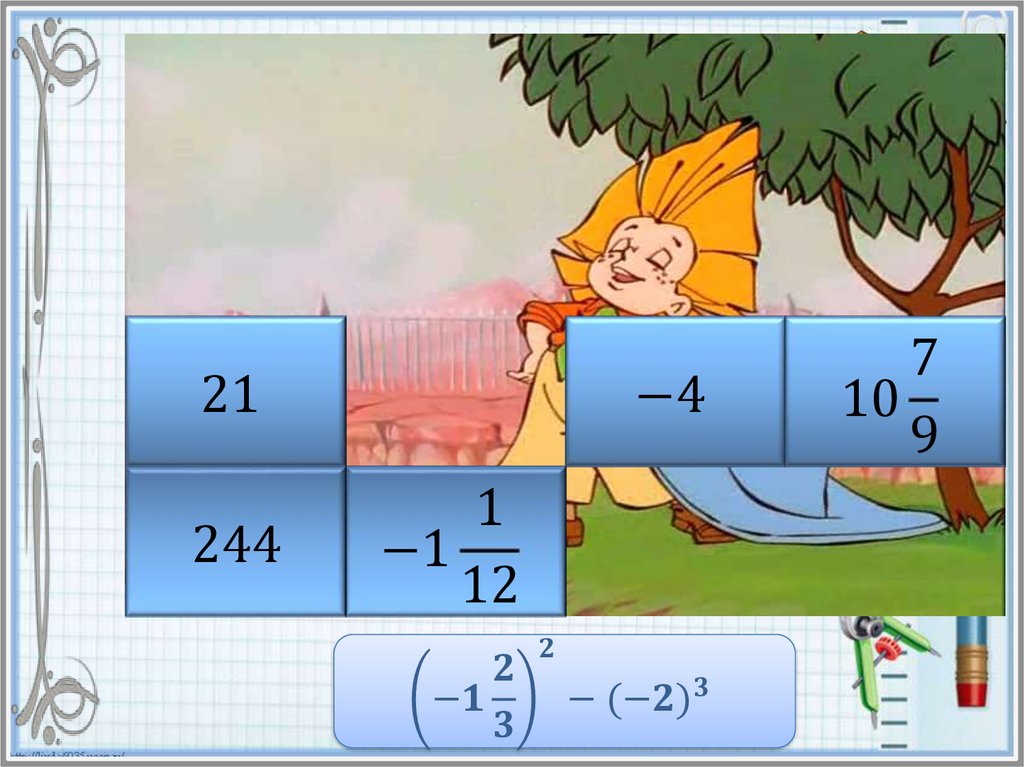
Найдите значение степени и в таблице ответов кликните на
карточку с числом левой кнопкой мыши. Если ответ
правильный, то откроется часть картинки. Если же вы
ошиблись, то решите пример заново и повторите попытку.
Перейти на следующий слайд можно с помощью кнопки
«дальше». Но для начала немного повторения из истории
возникновения степени.

3.

Нахождение значения степени называется
возведением в степень
Возведите в степень:
103
02
100
0
(-4)3
-64
(-5)2
25
Сделаем выводы:
При возведении в степень положительного числа получается…
При возведении в степень нуля получается…
При возведении в степень отрицательного числа получается…
Квадрат любого числа есть… число или… .

4.

Уже в самых древних математических текстах
Древнего Египта и Междуречья встречаются задачи на
вычисление степеней.
Одна из первых работ, где идет речь о данной функции, «Арифметика», которую создал древнегреческий математик
Диофант Александрийский.
Буквой Диофант
обозначал неизвестное и его степень. Особые обозначения имели
вторая степень неизвестного – «динамис»,
третья – «кубос»,
четвёртая – «динамо-динамис»,
пятая – «динамо-кубос», шестая –
«кубо- кубос».

5.

В Древней Индии ученые оперировали степенями
с натуральными показателями до девятой включительно,
называя их с помощью комбинации трех слов:
«ва» (2-я степень,
от слова «варга» - квадрат), «гха» (3-я степень, от «гхана» тело, куб) и «гхата» (слово, указывающее на сложение показателей).
Например, 4-ая степень – «ва-ва»,
5-ая – «ва-гха-гхата», 6-ая – «ва-гха».

6.

Нидерландский математик
Симон Стевин
в XVI - XVII веках предпринял
первые шаги к построению современной
теории степени.
Учёный обозначал неизвестную величину
кружком, а внутри его указывал показатели степени.
1
2
3
Его записи обозначали: