Решение текстовых задач. ОГЭ 2016

1.

Решение текстовых задач
ОГЭ 2016
Суровцева Е.И. учитель математики
МАОУ «Ухтинский технический
лицей им. Г.В.Рассохина» г.Ухта

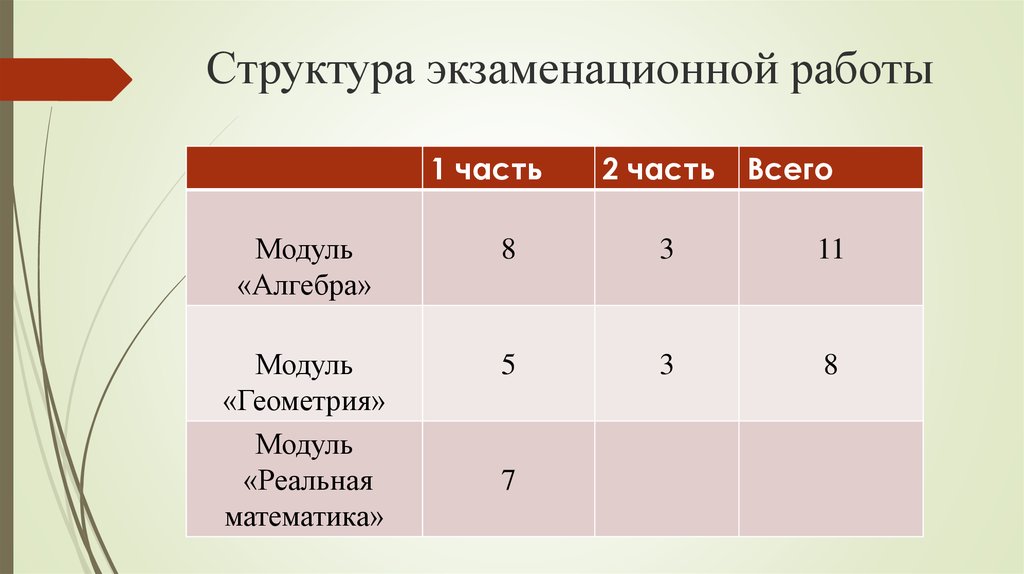
2. Структура экзаменационной работы

1 часть
2 часть
Всего
Модуль
«Алгебра»
8
3
11
Модуль
«Геометрия»
Модуль
«Реальная
математика»
5
3
8
7

3. Задания второй части:

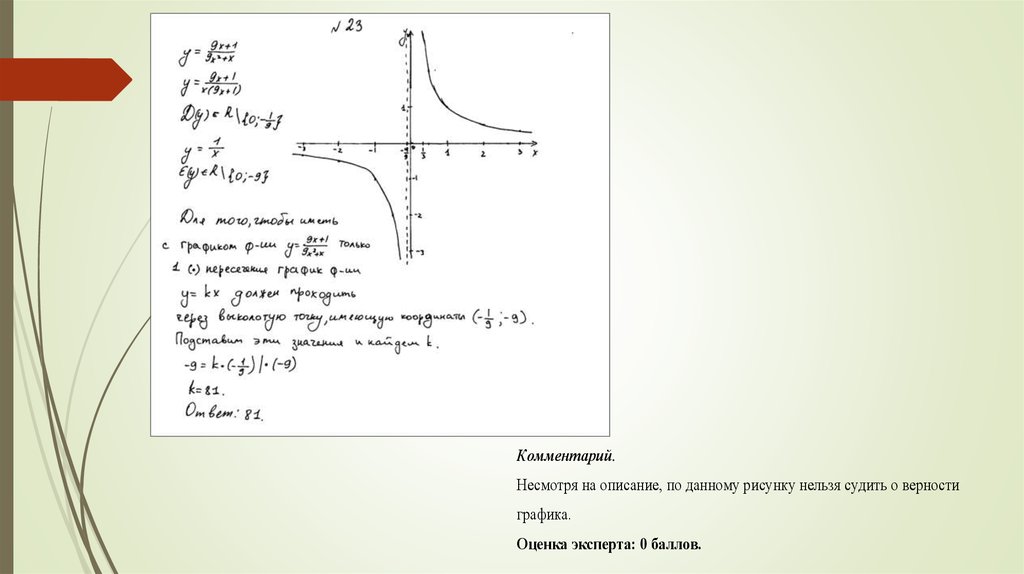
21(алгебра), 24 (геометрия) немногим превышают
обязательный уровень;
22 (алгебра), 25 (геометрия) более высокого уровня
23(алгебра), 26 (геометрия) требуют высокого уровня
математического развития

4.

Тематическая принадлежность заданий:
№21 – упрощение алгебраических выражений, решение уравнений,
решение систем уравнений,
№22 – решение текстовой задачи,
№23 – построение графика функции,
№24 – геометрическая задача на вычисление,
№25 – геометрическая задача на доказательство,
№26 – геометрическая задача высокого уровня сложности.

5. Шкала перевода в школьную отметку в 2016 году

Отметка по
пятибальной шкале
Суммарный балл за
работу в целом
2
3
0–7
8 – 14
4
5
15 – 21 22 – 32

6.

Результаты выполнения задания № 21
показатели
Полностью
выполнили задание
Частично
выполнили задание
Не выполнили
задание
Доля в %
8,85%
3,36%
87,79%
Результаты выполнения задания № 22
показатели
Полностью
выполнили задание
Частично
выполнили задание
Не выполнили
задание
Доля в %
3,38%
2,25%
94,38 %
Результаты выполнения задания № 23
показатели
Полностью
выполнили задание
Частично
выполнили задание
Не выполнили
задание
Доля в %
8,75%
2,82%
88,43%

7.

Результаты выполнения задания № 24
показатели
Полностью
выполнили задание
Частично
выполнили задание
Не выполнили
задание
Доля в %
3,22%
2,07%
94,7%
Результаты выполнения задания № 25
показатели
Полностью
выполнили задание
Частично
выполнили задание
Не выполнили
задание
Доля в %
9,08%
1,12%
89,8 %
Результаты выполнения задания № 26
показатели
Полностью
выполнили задание
Частично
выполнили задание
Не выполнили
задание
Доля в %
0,22%
0,06%
99,72%

8. Основные ошибки

9. Особое внимание

Умение читать и верно понимать условие задачи;
Решать практические задачи;
Выполнять арифметические действия, простейшие
алгебраические преобразования, действия с
основными функциями.

10. Внедрить в постоянную практику

11. Подходы к оцениванию

Решение математически грамотное и полное
Должен быть понятен ход рассуждения
Оформление произвольное

12. Решения и критерии оценивания второй части экзаменационной работы

13. Решения и критерии оценивания второй части экзаменационной работы

14. Решения и критерии оценивания второй части экзаменационной работы

15.

Комментарий.
Работа интересная – записан верный ответ. Но присутствуют в последних
строках:
а) ошибка в вычислении корня квадратного уравнения;
б) ошибка при сложении чисел с разными знаками;
в) ошибка в формуле корней квадратного уравнения;
г) ошибка при делении чисел с разными знаками.
Оценка эксперта: 0 баллов.

16.

Комментарий.
При нахождении корней квадратного уравнения допущена неверная запись.
При
наличии
общей
формулы
для
нахождения
корней
квадратного
уравнения, записанной верно, не извлечен корень из дискриминанта, все
дальнейшие
вычисления
(с
этой
ошибкой)
выполнены
верно.
Вычислительная ошибка присутствует, с её учётом дальнейшие шаги
выполнены верно.
Оценка эксперта: 1 балл.

17.

Комментарий.
Все этапы решения присутствуют, корни в правом столбце найдены верно.
Неверную запись ответа можно рассмотреть как описку.
Оценка эксперта: 1 балл.

18.

Комментарий.
Правильно выполнены преобразования, получен верный ответ.
Оценка эксперта: 2 балла.

19.

Комментарий.
Все этапы решения присутствуют, корни найдены верно. Неверную запись
ответа можно рассмотреть как неверное владение символикой (хочется
надеяться, что учащийся хотел написать фигурные скобки).
Оценка эксперта: 1 балл.

20. Пример оценивания задания 22

Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за
30 часов. За какое время покрася забор мальчики, работая втроем? Ответ дайте в минутах

21.

Комментарий.
Ход решения верный, ответ верный.
Оценка эксперта: 2 балла.

22.

Комментарий.
Логическая ошибка – выпускник перепутал производительность и время.
Оценка эксперта: 0 баллов.

23.

Комментарий.
Ход решения верный, ответ верный.
Оценка эксперта: 2 балла.

24.

Комментарий.
Арифметическая ошибка на последнем шаге.
Оценка эксперта: 1 балл.

25.

Пример оценивания решения задания 23.
Постройте график функции y
9x 1
и определите, при каких значениях k
9x2 x
прямая y kx имеет с графиком ровно одну общую точку.
Ответ: 81.
Комментарий.
График построен неверно – отсутствует выколотая точка. В соответствии с
критериями – 0 баллов.
Оценка эксперта: 0 баллов.

26.

Комментарий.
Несмотря на описание, по данному рисунку нельзя судить о верности
графика.
Оценка эксперта: 0 баллов.

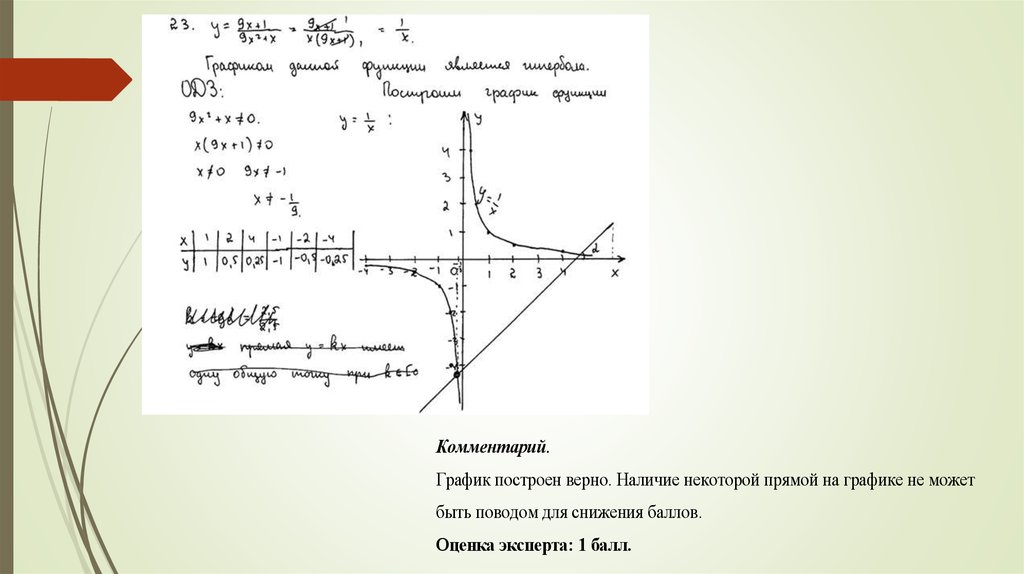
27.

Комментарий.
График построен верно. Наличие некоторой прямой на графике не может
быть поводом для снижения баллов.
Оценка эксперта: 1 балл.

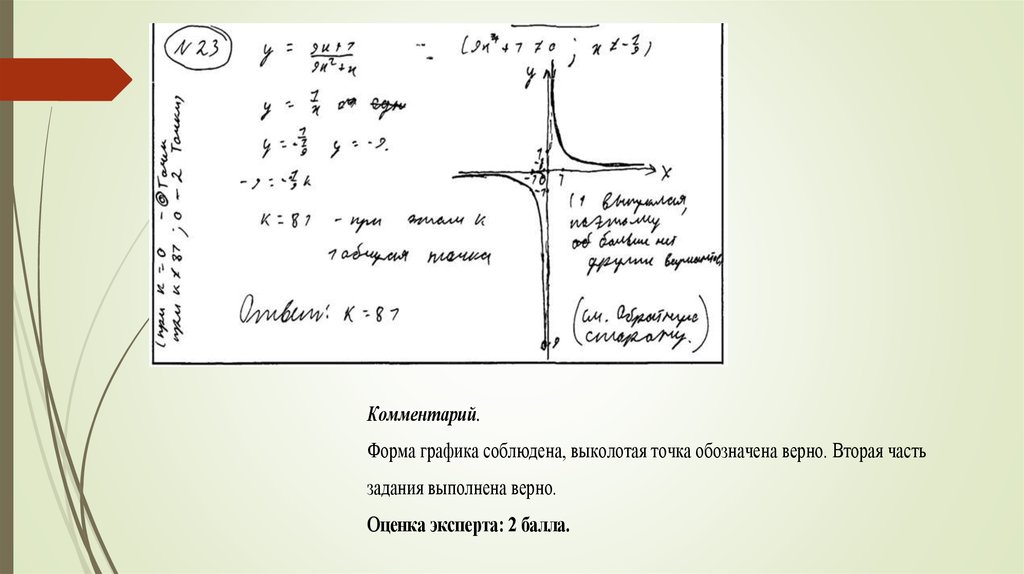
28.

Комментарий.
Форма графика соблюдена, выколотая точка обозначена верно. Вторая часть
задания выполнена верно.
Оценка эксперта: 2 балла.

29. Типы задач № 22

Процентные доли веществ в смеси
Подсчет средней скорости
Движение по дороге
Встречное движение по дороге
Движение с опережением по дороге
Движение по реке
Совместная работа
Доли или проценты

30. Смешав 70%-й и 60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды

добавили 2 кг 90%-го раствора той же
кислоты, то получили бы 70%-й раствор кислоты. Сколько
килограммов 70%-го раствора использовали для получения
смеси?

31.

Решение:
Пусть х кг масса первого раствора, у кг масса второго раствора.
I раствор
II раствор
Вода
Всего
I раствор
II раствор
III раствор
Всего
Масса, кг
% вещества
Х
У
2
х + у+ 2
70
60
50
Масса, кг
% вещества
Х
У
2
х + у+ 2
70
60
90
70
Составим систему уравнений:
0,7х + 0,6у = 0,5(х + у + 2)
0,7х + 0,6у + 1,8 = 0,7(х + у + 2)
Ответ : 3
Масса
вещества, кг
0,7х
0,6у
0,5(х + у + 2)
0,7х + 0,6у = 0,5(х + у + 2)
Масса
вещества, кг
0,7х
0,6у
1.8
0,7(х + у + 2)
0,7х + 0,6у +1,8= 0,7(х + у +2)

32.

Рыболов в 5 часов утра отправился на моторной лодке к затону,
удаленному от пристани на 6 км вверх по реке. Там он в
течении 3 часов ловил рыбу, после чего отправился обратно и
вернулся на пристань в 10 часов утра. Найдите скорость
течения реки, если известно, что собственная скорость лодки
была постоянна во время всего пути и равна 8 км/ч.
Ответ 4 км/ч

33.

Из А в В одновременно выехали два автомобиля. Первый
проехал с постоянной скоростью весь путь. Второй проехал
первую половину пути со скоростью, меньшей скорости
первого на 16 км/ч, а вторую половину пути проехал со
скоростью 96 км/ч, в результате чего прибыл в В
одновременно с первым автомобилем. Найдите скорость
первого автомобиля, если известно, что она больше 60 км/ч.
Ответ: 64 км/ч.

34.

По двум параллельным железнодорожным путям в одном
направлении следуют пассажирский и товарный поезда.
Скорость пассажирского поезда равна 80 км/ч, и, догнав
товарный поезд, он прошёл мимо него за 90 секунд. Найдите
скорость товарного поезда, если его длина составляет 600
метров, а длина пассажирского поезда составляет 300 метров.
Ответ 44 км/ч.

35.

Первая труба наполняет резервуар на 16 минут дольше, чем
вторая. Обе трубы вместе наполняют этот же резервуар за 15
минут. За сколько минут наполняет этот резервуар первая
труба?
Ответ: 40
Сережа и Дима красят забор за 14 часов. Сережа и Костя
красят этот же забор за 15 часов, а Костя и Дима -- за 35 часов.
За сколько часов мальчики покрасят забор, работая втроем?
Ответ: 12

36.

Два сплава, из которых первый содержит 40% , а второй
содержит 60% никеля, сплавили друг с другом, получив 200 кг
сплава, содержащего 55% никеля. Сколько килограммов
составляла масса первого сплава?
Ответ: 50

37.

Сразу после сбора урожая процентное содержание воды в
бананах составляет 75%. После их перевозки процентное
содержание воды в них становится равным 70%. Сколько
килограммов бананов надо приобрести, чтобы после
перевозки осталось 2500 кг бананов?
Ответ: 3000 кг.