Similar presentations:
Формирование математических способностей учащихся через развитие логического мышления
1. Формирование математических способностей учащихся через развитие логического мышления. учитель математики Абдрахмановой С.А.
2.
«Все дети одареныот природы»
«Если хочешь увидеть результат, будь готов много
работать»
Мария Берсенева
3.
Целью обучения математики в школе является не толькоовладение конкретными математическими знаниями, но и
интеллектуальное развитие учащихся, формирование качеств
мышления, характерных для математической деятельности и
необходимых человеку для продуктивной жизни в обществе.
В настоящий момент образование характеризуется как процесс
обучения и воспитания в интересах личности, общества и
государства, направленный на развитие индивида, его
индивидуальных, умственных и физических способностей,
одаренности и таланта.
4. Основные формы работы учителей с одаренными детьми
Основные формы работы учителейодаренными детьми
факультативы
кружки
творческие мастерские;
работа по индивидуальным планам
занятия исследовательской деятельностью;
участие в конкурсах
научно-практические конференции;
подготовка к олимпиадам
с
5.
Программа факультативного курсапо математике
(решение логических задач)
Автор: учитель математики
Абдрахманова С.А.
2014-2015 уч.г.
6.
Цель: Организация работы с учащимися, имеющимиповышенный уровень мотивации, включение учащихся в
исследовательскую деятельность.
Задачи:
- формирование у учащихся устойчивого интереса к
математике;
- выявление и развитие математических способностей;
- овладение конкретными математическими знаниями,
необходимыми для применения в практической деятельности;
- интеллектуальное развитие учащихся, формирование качеств
мышления, характерных для математической деятельности;
- формирование представлений о математике как части
общечеловеческой культуры, понимание значимости математики
для общественного прогресса;
- подготовка к сознательному усвоению систематического курса
алгебра и геометрия;
- формирование навыков перевода различных задач на язык
математики.
7.
Содержание:Задачи на разрезание и складывание фигур.
(игра Танграм.)
Задачи, решаемые с помощью графов.
Задачи с использованием схем и таблиц.
Задачи с отношениями
Задачи на переправу.
Задачи на проценты
Занимательные задачи.
Задачи на переливания.
Математические игры
Текстовые задачи
Задачи с геометрическим содержание
Итоговое занятие
- 3 часа
- 3 часа
- 3 часа
-3 часа
- 3 часа
- 3 часа
- 3 часа
-3 часа
-3 часа
-3 часа
-3 часа
- 1 час
8.
"Очарование танграма состоит в простоте материала и в кажущейся егонепригодности для создания фигурок, обладающих эстетической
привлекательностью»
М. Гарднера
9.
Танграм развивает:•логическое мышление, фантазию;
•пространственное воображение;
•сообразительность;
•способность к комбинированию;
• наглядно-образное мышление, внимание;
•восприятие, комбинаторные способности;
•мелкую маторику;
•творческие способности
учит:
• последовательности и терпению;
•усидчивости;
• умению играть по правилам и выполнять инструкции;
• упорству в достижении цели;
• пониманию цвета, величины и формы.
10.
Темы для исследовательской деятельности:1. Головоломки .Их виды.
2. История возникновения игры «Танграм».
3. Мифы о создании игры «Танграм».
4. «Танграм» в литературных произведениях и в
жизни замечательных людей;
5. Танграм. Новые идеи и возможности .
11.
Правила:В каждую собранную фигуру должны входить все
семь элементов.
При составлении фигур элементы не должны
налегать друг на друга.
Элементы фигур должны примыкать один к
другому.
Начинать нужно с того, чтобы найти место
самого большого треугольника.
12.
13.
Вывод:Танграм может применяться на уроках математики для получение начальных
сведений о геометрии. Знакомство с простейшими геометрическими фигурами:
квадрат, треугольник, ромб, знакомство с углами. Сравнение фигур по форме,
размеру, площади.
Составление из нескольких фигур новой геометрической фигуры: из двух
треугольников – ромб, большой треугольник, квадрат, из трёх – треугольник,
трапецию, параллелограмм и т.д.
Играя, мы запоминаем названия геометрических фигур, их свойства,
отличительные признаки, обследуем формы зрительным и осязательнодвигательным путем, свободно перемещаем их с целью получения новой
фигуры. У нас развивается умение анализировать простые изображения,
выделять в них и в окружающих предметах геометрические формы, практически
видоизменять фигуры путем разрезания и составлять их из частей.
14. Графы
Задачи, решаемые с помощью графов.15. Проведение поиска способа и осуществления решения задачи нуждается в следующих способностях :
абстрагирования;моделирования,
гибкого применения теории графов,
применения всех известных математических
способов решения.
16. Основные этапы при решении задач:
1 этап: заключается в том, что бы суметьпроанализировать и закодировать условия задачи.
2 этап: схематическая запись. состоит в
геометрическом представлении графов, и на этом
этапе элемент творчества очень важен потому, что
далеко не просто найти соответствия между
элементами условия и соответствующими
элементами графа.
Все остальные этапы тоже не обходятся без
применения творчества и изобретательности.
17. Что такое граф?
Граф- геометрическая фигура, состоящая източек(вершины графа) и линий , их
соединяющих(рёбра графа).
Слово «граф» в математике означает картинку,
где нарисовано несколько точек, некоторые из
которых соединены линиями.
В математике определение графа дается так:
графом называется конечное множество точек,
некоторые из которых соединены линиями.
18.
Схема графа, состоящая из«изолированных» вершин,
называется нулевым графом
Графы, в которых не построены все
возможные ребра, называются
неполными графами
Графы, в которых построены все
возможные ребра, называются
полными графами
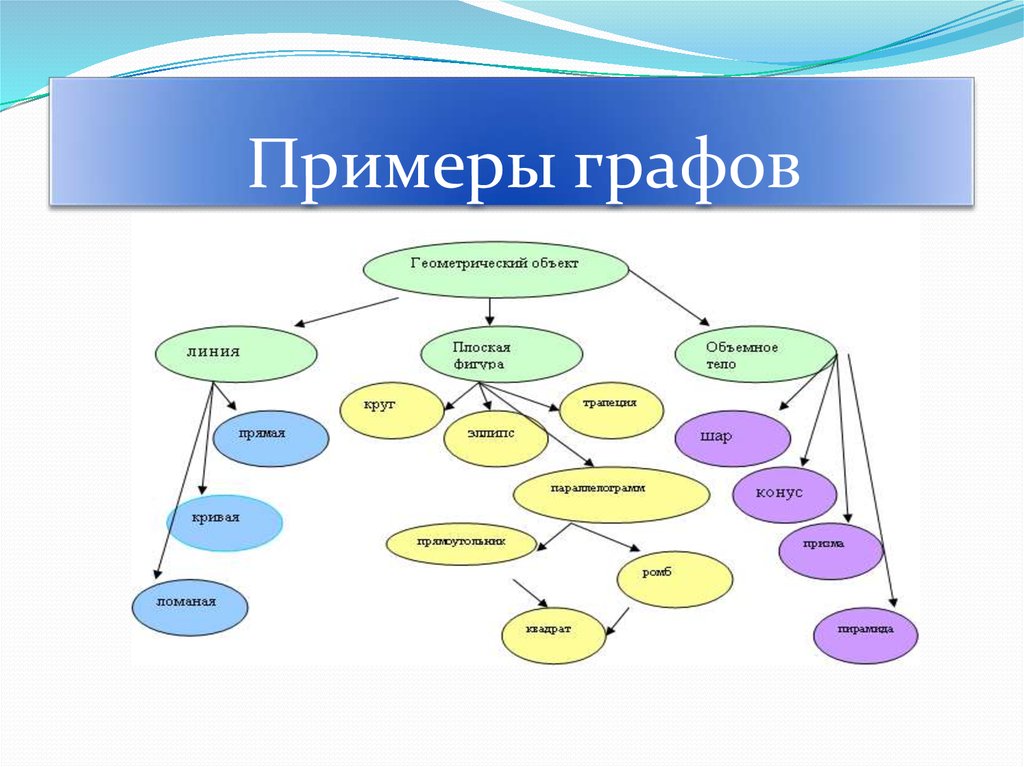
19. Примеры графов
20. Дерево – это граф, в котором две любые вершины соединены ровно одним простым путём.
код1
2
3
2
4
1
2
4
3
3
4
1
2
3
4
1
2
3 4
21. Кенигсбергские мосты
22. Кенигсбергские мосты
Можно ли обойти все Кенигсбергские мосты,проходя только один раз через каждый из этих
мостов?
23. Представим задачу в виде графа,где вершины – острова и берега (A,B,C,D), а ребра – мосты
СД
А
В
Важно, является ли число мостов, ведущих к этим
отдельным участкам, четным или нечетным.
Так, в нашем случае к участку A ведут пять мостов, а к
остальным – по три моста.
24.
3С
5
Д
А
В
3
3
Какие вершины четные, а какие нечетные? Подпишем степени
вершин в кружочках.
Нечетные вершины: А, B, C, D.
Вывод: нельзя
25. Алгоритм решения задач
1. Нарисовать граф, где вершины – острова и берега, аребра – мосты.
2. Определить степень каждой вершины и подписать
возле нее.
3. Посчитать количество нечетных вершин.
4. Обход возможен:
a. ЕСЛИ все вершины – четные, и его можно начать с
любого участка.
b. ЕСЛИ 2 вершины – нечетные, но его нужно начать с
одной из нечетных местностей.
5. Обход невозможен, если нечетных вершин больше 2.
6. Сделать ВЫВОД.
7. Указать Начало и Конец пути.
26.
Задача о 15 мостахВ некоторой местности через протоки переброшено 15
мостов.
Можно ли обойти все мосты ,проходя по каждому мосту только один раз?
27. Построим граф, где вершины – острова и берега, а ребра – мосты.
ED
С
А
В
F
определить степень каждой вершины и узнать
какие вершины четные, а какие нечетные.
28. .
E3
D
8
С
4
5
4
В
А
6
F
Нечетные вершины: D, E.
ВЫВОД: Так как количество нечетных вершин = 2, то обход возможен.
Его Начало может быть в местности D, а Конец в местности E.
29. Решение логических задач табличным способом и с помощью графиков.
30. - Что такое таблицы? Это форма представления информации, где информация:
систематизировананаглядна и емка
ее части взаимосвязаны
имеют логическую зависимость
31. Задача № 1
В школе учатся 4 талантливых мальчика: Иванов, Петров,Сидоров и Андреев. Один из них – будущий музыкант,
другой преуспел в бальных танцах, третий – солист хора
мальчиков, четвертый подает надежды как художник.
О них известно следующее:
1. Иванов и Сидоров присутствовали в зале
консерватории, когда там солировал в хоре мальчиков
певец.
2. Петров и музыкант вместе позировали художнику.
3. Музыкант раньше дружил с Андреевым, а теперь хочет
познакомиться с Ивановым.
4. Иванов не знаком с Сидоровым, т.к. они учатся в
разных классах и в разные смены.
Кто чем увлекается?
32. 1. Иванов и Сидоров присутствовали в зале консерватории, когда там солировал в хоре мальчиков певец → Иванов и Сидоров не певцы
ТанцорИванов
Художник
Солист
-
Петров
Сидоров
Андреев
-
Музыкант
33. 2. Петров и музыкант вместе позировали художнику → Петров – не художник и не музыкант
ТанцорХудожник
Иванов
Петров
Сидоров
Андреев
Солист
Музыкант
-
-
34. 3. Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться с Ивановым → Андреев и Иванов – не музыканты → Музыкант –
Сидоров.Танцор
Художник
Иванов
Петров
Сидоров
Андреев
Солист
Музыкант
-
-
-
-
+
-
35. 4. Так как Сидоров – музыкант, он не может быть ни солистом, ни танцором, ни художником.
ТанцорХудожник
Иванов
Петров
Сидоров
Андреев
Солист
Музыкант
-
-
-
-
-
+
-
36. 4. Так как Сидоров – музыкант, он не может быть ни солистом, ни танцором, ни художником.
ТанцорХудожник
Иванов
Петров
Сидоров
Андреев
Солист
Музыкант
-
-
-
-
-
+
-
37. 5. Петров и Сидоров вместе позировали художнику, но Иванов не знает Сидорова, значит художник – не Иванов → художник – Андреев
ТанцорХудожник
Солист
Музыкант
Иванов
-
-
-
Петров
-
-
Сидоров
-
-
-
+
Андреев
-
+
-
-
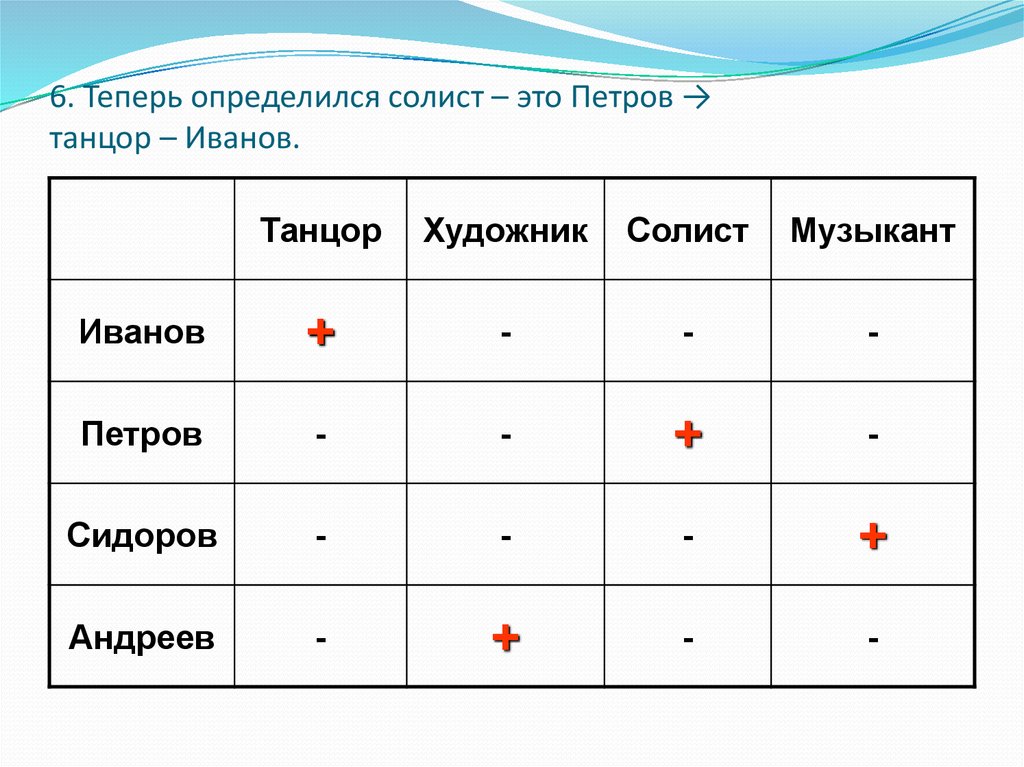
38. 6. Теперь определился солист – это Петров → танцор – Иванов.
ТанцорХудожник
Солист
Музыкант
Иванов
+
-
-
-
Петров
-
-
+
-
Сидоров
-
-
-
+
Андреев
-
+
-
-
39.
Решение задач с помощью графиков :О них известно следующее:
1. Иванов и Сидоров присутствовали в зале консерватории, когда там солировал в
хоре мальчиков певец.
2. Петров и музыкант вместе позировали художнику.
3. Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться с
Ивановым.
4. Иванов не знаком с Сидоровым, т.к. они учатся в разных классах и в разные
смены.
Кто чем увлекается?
Иванов
Музыкант
Петров
Танцор
Сидоров
Солист
Андреев
Художник
40. Самостоятельная работа
41. Задача 2
Маша, Оля, Лена и Валя – замечательныедевочки. Каждая из них играет на каком-нибудь
музыкальном инструменте и говорит на одном из
иностранных языков. Инструменты и языки у
них разные. Маша играет на рояле. Девочка,
которая говорит по-французски, играет на
скрипке. Оля играет на виолончели. Маша не
знает итальянского языка, а Оля не владеет
английским. Лена не играет на арфе , а
виолончелистка не говорит по-итальянски.
Нужно определить, на каком инструменте играет
каждая из девочек и каким иностранным языком
она владеет.
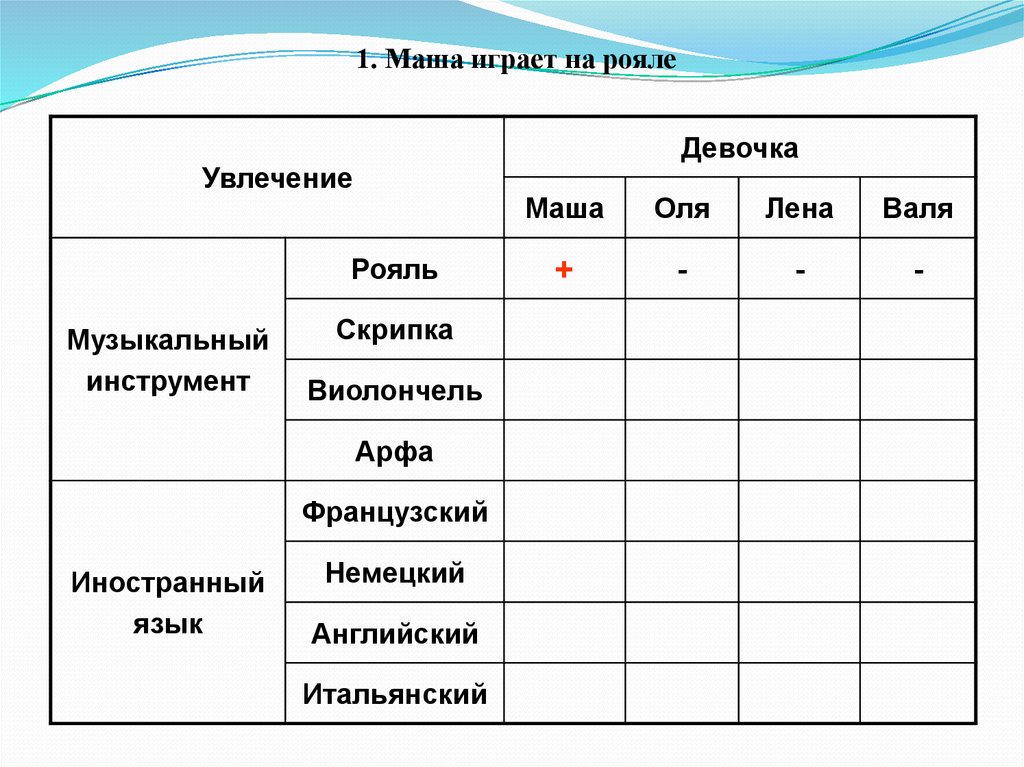
42.
1. Маша играет на роялеДевочка
Увлечение
Рояль
Музыкальный
инструмент
Скрипка
Виолончель
Арфа
Французский
Иностранный
язык
Немецкий
Английский
Итальянский
Маша
Оля
Лена
Валя
+
-
-
-
43.
2. Оля играет на виолончелиДевочка
Увлечение
Рояль
Музыкальный
инструмент
Оля
Лена
Валя
+
-
-
-
-
+
-
-
Скрипка
Виолончель
Арфа
Французский
Иностранный
язык
Маша
Немецкий
Английский
Итальянский
44.
3. Маша не знает итальянского языка, а Оля не владеет английскимДевочка
Увлечение
Рояль
Музыкальный
инструмент
Маша
Оля
Лена
Валя
+
-
-
-
-
+
-
-
Скрипка
Виолончель
Арфа
Французский
Иностранный
язык
Немецкий
Английский
Итальянский
-
45.
4. Лена не играет на арфе → на арфе играет Валя, а на скрипке –Лена. Виолончелистка не говорит по-итальянски
Девочка
Увлечение
Музыкальный
инструмент
Маша
Оля
Лена
Валя
Рояль
+
-
-
-
Скрипка
-
-
+
-
Виолончель
-
+
-
-
Арфа
-
-
-
+
Французский
Иностранный
язык
Немецкий
Английский
Итальянский
-
-
46.
5. Девочка, которая говорит по-французски, играет на скрипке → пофранцузски говорит Лена → по-итальянски – Валя.Девочка
Увлечение
Музыкальный
инструмент
Иностранный
язык
Маша
Оля
Лена
Валя
Рояль
+
-
-
-
Скрипка
-
-
+
-
Виолончель
-
+
-
-
Арфа
-
-
-
+
Французский
-
-
+
-
-
+
Немецкий
Английский
Итальянский
-
-
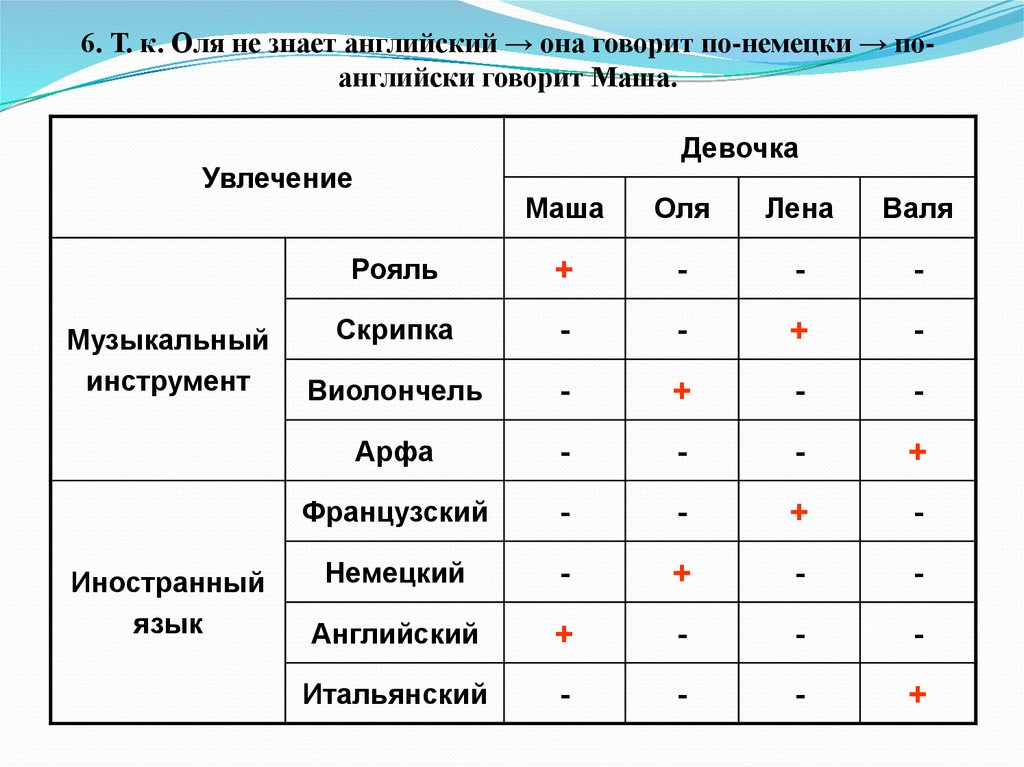
47.
6. Т. к. Оля не знает английский → она говорит по-немецки → поанглийски говорит Маша.Девочка
Увлечение
Музыкальный
инструмент
Иностранный
язык
Маша
Оля
Лена
Валя
Рояль
+
-
-
-
Скрипка
-
-
+
-
Виолончель
-
+
-
-
Арфа
-
-
-
+
Французский
-
-
+
-
Немецкий
-
+
-
-
Английский
+
-
-
-
Итальянский
-
-
-
+
48.
6. Т. к. Оля не знает английский → она говорит по-немецки → поанглийски говорит Маша.Девочка
Увлечение
Музыкальный
инструмент
Иностранный
язык
Маша
Оля
Лена
Валя
Рояль
+
-
-
-
Скрипка
-
-
+
-
Виолончель
-
+
-
-
Арфа
-
-
-
+
Французский
-
-
+
-
Немецкий
-
+
-
-
Английский
+
-
-
-
Итальянский
-
-
-
+
49.
Ф.И.
А.
Н.
50.
Заключение:Работать с одаренными, способными детьми
– сплошное удовольствие, к сожалению не все
дети могут проявляют такие способности. А
возможно, даже и к счастью. В любом случае,
работать с ними следует в особом порядке,
чтобы не позволить им утратить эти
способности и любовь к математике.
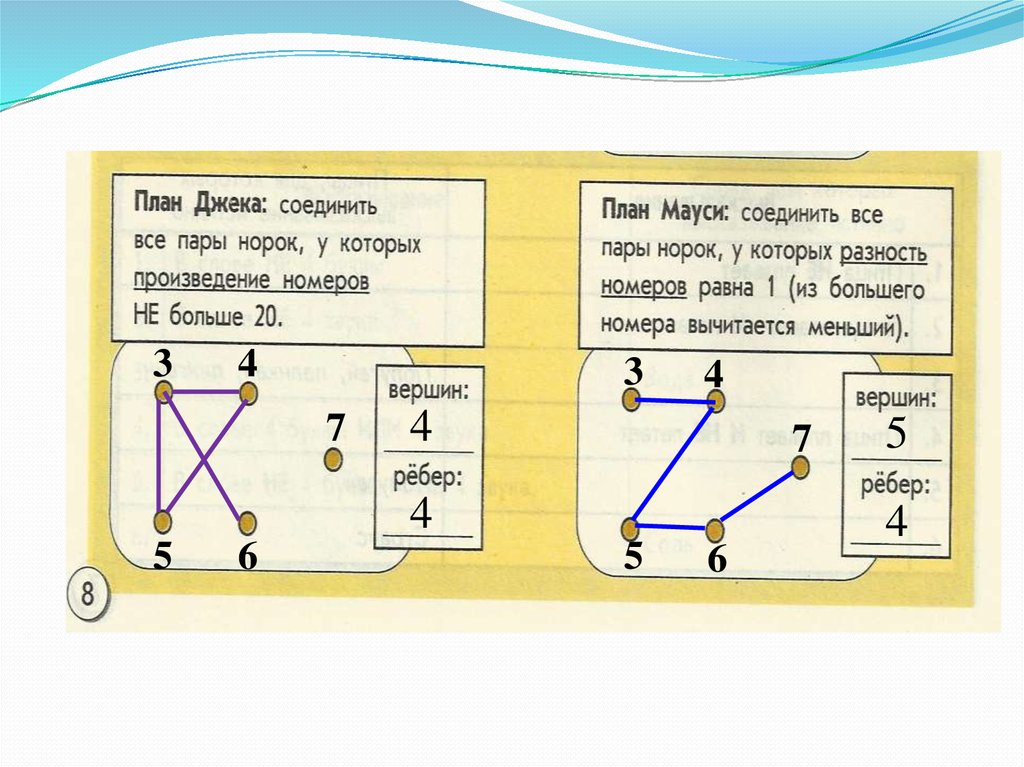
51. Простейшие задачи на графы
34
7
5
6
5
6
52.
34
3
7
4
4
7
4
5
6
5
6
5
4
53.
34
3
7
4
7
3
2
5
6
5
4
5
6

















































 informatics
informatics








