Similar presentations:
Натуральные и целые числа
1. Презентация учителя математики МБОУ СОШ № 14 пгт Ильского МО Северский район Барабаш Ирины Викторовны
2. 02.09.11. Классная работа
Натуральные и целые числа3. Числа, используемые для счета предметов, т.е. числа 1,2,3,4,5,…, называются натуральными числами.
• При сложении и умножении натуральныхчисел получим натуральное число.
• При вычитании и делении натуральных
чисел натуральное число получим не
всегда.
Например: 3 – 5
1:2
4. Натуральные числа, число ) и числа -1, -2, -3, -4, -5, … называют целыми числами
• Натуральные числа называют целымиположительными.
• Натуральные числа и число ) называют
неотрицательными числами.
5. Множество натуральных чисел обозначают N. Множество целых чисел – Z. Множество целых положительных – Множество целых
отрицательных –Z
Z
6. n – натуральное число
n N7. m – целое число
m Z8. Множество натуральных чисел часть множества целых чисел (подмножество)
N Z9. Делимость натуральных чисел
Пусть даны два натуральных числа –a и b.
Число a делится на число b, если
существует такое число q, что a = b q.
a – делимое
b – делитель
q - частное
10. Из записи a = b q следует, что b – делитель a и что a кратно b
a b11. Свойство 1 Если и , то Например.
Свойство 1Если
a c
и
c b
, то
a b
Например.
48 6
6 3
48 3
12. Свойство 2 Если и , то Например.
Свойство 2Если
a b
и
c b
, то
(a c) b
Например.
12 3
21 3
(12 21) 3
13. Свойство 3 Если и c не делиться на b, то (a + c) не делиться на b
Свойство 3Если
a b
и c не делиться на b, то
(a + c) не делиться на b
14. Свойство 4 Если и , то Например.
Свойство 4Если
a b
и
(a c) b ,
то
c b
Например.
12 3
(12 21) 3
21 3
15. Свойство 5 Если и , то Например.
Свойство 5Если
a b1
и
c b2 ,
то
ac b1b2
Например.
12 3
28 7
(12 21) (3 7)
16. Свойство 6 Если и c – любое натуральное число, то ; если , то Например.
Свойство 6Если a b и c – любое натуральное
число, то ac bc ;
если
ac bc
, то
a b
Например.
12 3
(12 5) (3 5)
17. Свойство 7 Если и c – любое натуральное число, то . Например.
Свойство 7Если a b
число, то
и
c – любое натуральное
ac b
.
Например.
12 3
(12 5) 3
18. Свойство 8 Если и , то для любых натуральных чисел n и k справедливо соотношение Например.
Свойство 8a b
c b
Если
и
, то для любых
натуральных чисел n и k справедливо
соотношение
(an ck ) b
Например.
12 3
21 3
(25 12 271 21) 3
19.
20.
21.
22.
23.
24. Дома
• Ч1 с. 5- 9 (конспект учить)• Ч 2 с. 5 № 1(в,г), 2(в,г),3(а,б), с.13 №1.6.









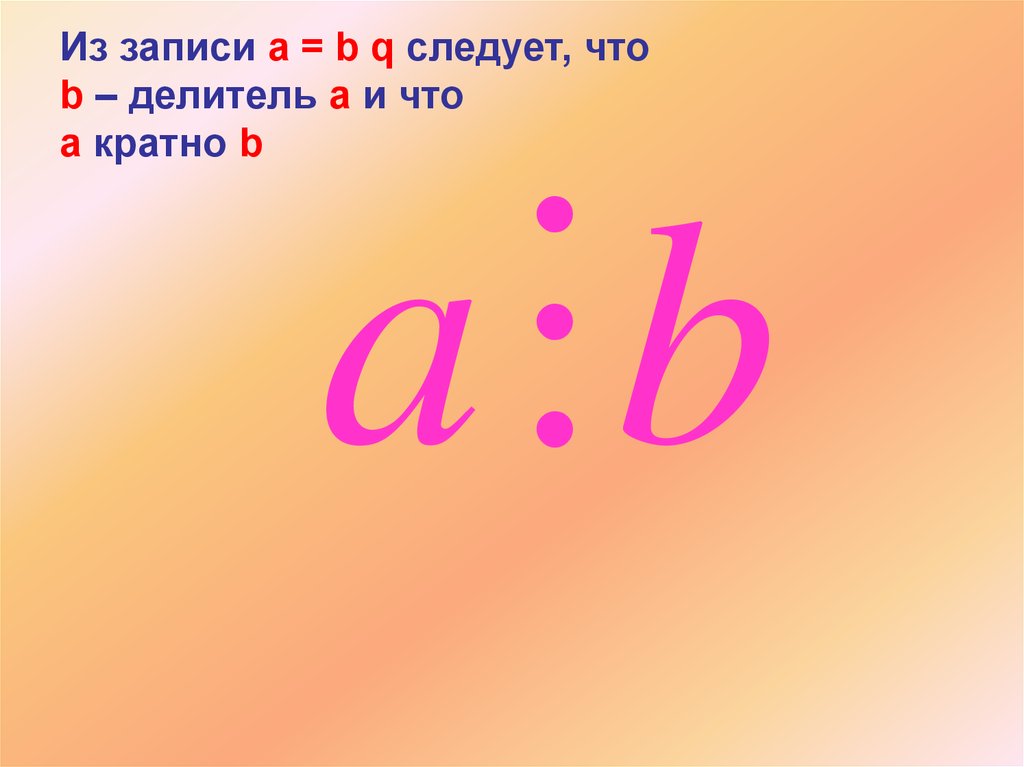














 mathematics
mathematics








