Similar presentations:
Расположение фигур в декартовой системе координат
1. Прототип задания B3 (№27564)
МатематикаПрототип задания B3 (№27564)
2. Прототип задания B3 (№ 27564)
Найдите площадь треугольника, вершины которогоимеют координаты (1;6), (9;6), (7;9)
S₁ =½(a·h)
S₁ =½(8·3) = 12
3 h
2 способ решения
9-1=8
Ответ: 12
3. Прототип задания B3 (№ 27564)
Найдите площадь треугольника, вершины которогоимеют координаты (1;6), (9;6), (7;9)
Если из площади прямоугольника вычесть площади двух площадей
зеленых треугольников, то получим площадь искомого треугольника.
9-1= 8
3
Площадь прямоугольника равна: 3·8 = 24
S₂
S₁
S₁ =½(6·3) = 9
9-6= 3
S₂ = =½(2·3) = 3
Площадь искомого треугольника равна: 24 – 9 – 3 = 12
2
6
Ответ: 12
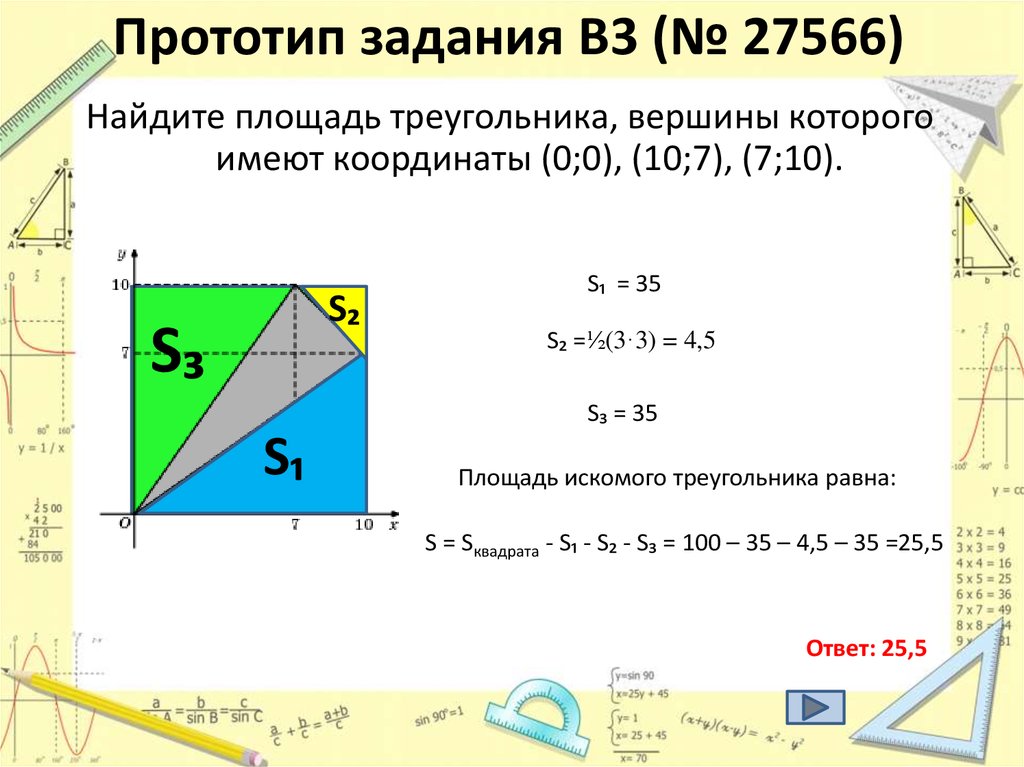
4. Прототип задания B3 (№ 27566)
Найдите площадь треугольника, вершины которогоимеют координаты (0;0), (10;7), (7;10).
S₂
S₃
S₁ = 35
S₂ =½(3·3) = 4,5
S₃ = 35
S₁
Площадь искомого треугольника равна:
S = Sквадрата - S₁ - S₂ - S₃ = 100 – 35 – 4,5 – 35 =25,5
Ответ: 25,5
5. Прототип задания B3 (№ 27570)
Найдите площадь четырехугольника, вершиныкоторого имеют координаты (8;0), (9;2), (1;6), (0;4).
Данный четырехугольник является прямоугольником,
т.к. противоположные стороны раны.
Sпрямоугольника = a·b
b
Гипотенуза
a по теореме Пифагора равна:
а 8 2 4 2 64 16 80
а
2
1
Sпрямоугольника =
Гипотенуза
b по теореме Пифагора равна:
b 12 2 2 5
80 5 400 20
Ответ: 20
6. Прототип задания B3 (№ 27572)
Найдите площадь трапеции, изображенной на рисунке.Sтрапеции =
6-2=4
a+b
̶̶̶̶ ̶̶̶̶ ̶̶̶̶ ̶̶̶̶ ̶̶̶̶ h
2
Sтрапеции =
2+4
̶̶̶̶ ̶̶̶̶ ̶̶̶̶ ̶̶̶̶ ̶̶̶̶ ·3 = 9
2
3
3-1=2
Ответ: 9
7. Прототип задания B3 (№ 27574) Прототип задания B3 (№ 27575)
Прототип задания B3 (№ 27574)Найдите площадь
параллелограмма,
изображенного на рисунке.
Прототип задания B3 (№ 27575)
Найдите площадь
четырехугольника, вершины
которого имеют координаты
(1;7), (8;2), (8;4), (1;9).
3
2
2
7
Ответ: 6
Ответ: 14
8.
Использованы материалы сайтов:http://www.mathege.ru:8080/or/ege/Main.html?view=Pos
http://live.mephist.ru/show/mathege2010/view/B1/solved/








 mathematics
mathematics








