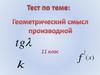На рисунке изображен график функции. Определите количество целых точек , в которых производная функции положительна

На рисунке изображен график функции. Найти количество точек на отрезке (-8;3), в которых касательная к графику функции

На рисунке изображен график производной функции. Найти промежутки возрастания функции. В ответе запишите количество целых

Изображен график производной функции. Найти точку максимума на отрезке (-3;3)

1.76M

Category: $mathematics$ mathematics

Геометрический смысл производной. Подготовка к ЕГЭ В9

1. Подготовка к ЕГЭ В9

Балагурова-Шемота, лицей№ 90

2.

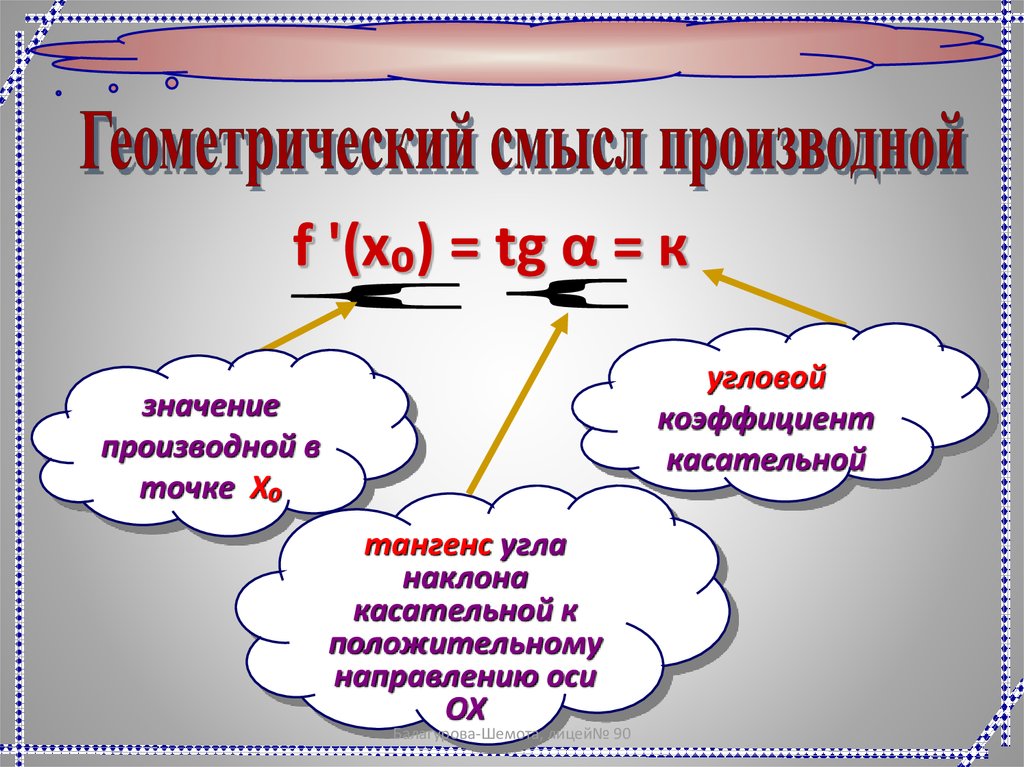
f '(x₀) = tg α = к
угловой
коэффициент
касательной
значение
производной в
точке Х₀
тангенс угла
наклона
касательной к
положительному
направлению оси
ОХ
Балагурова-Шемота, лицей№ 90

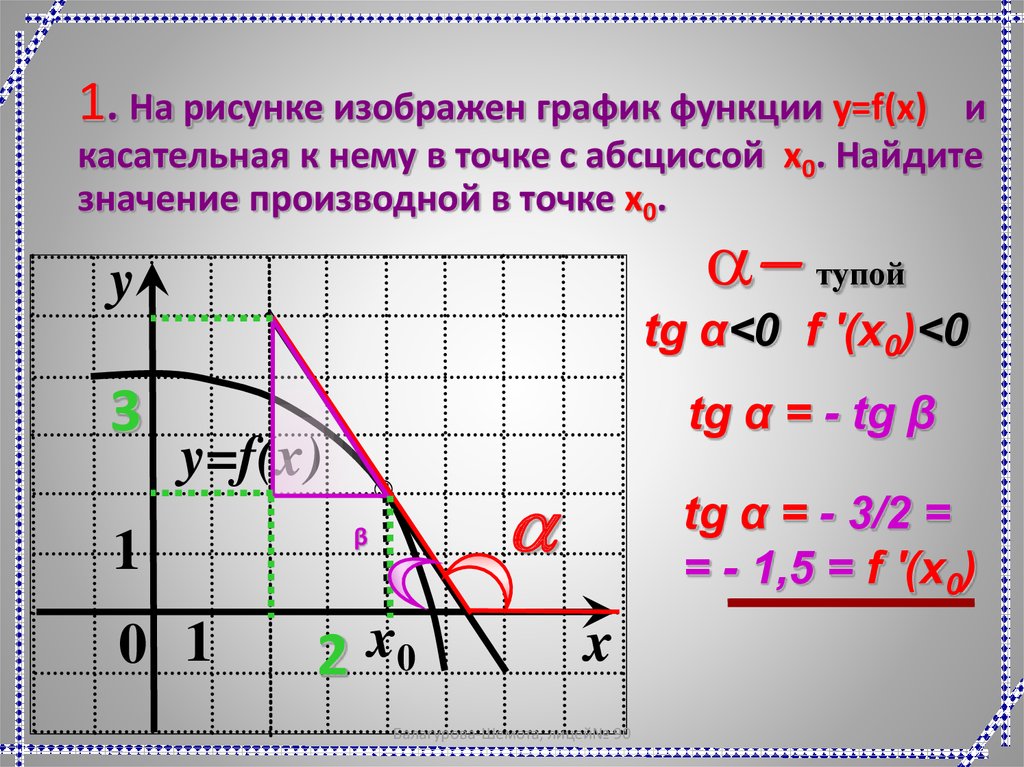
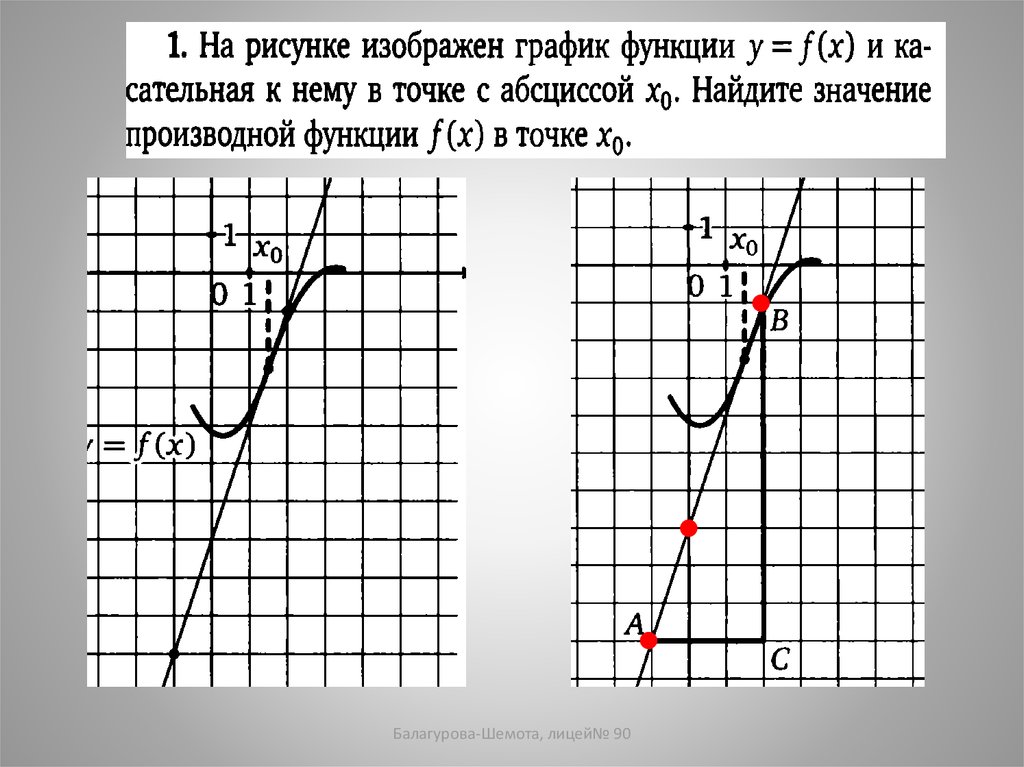
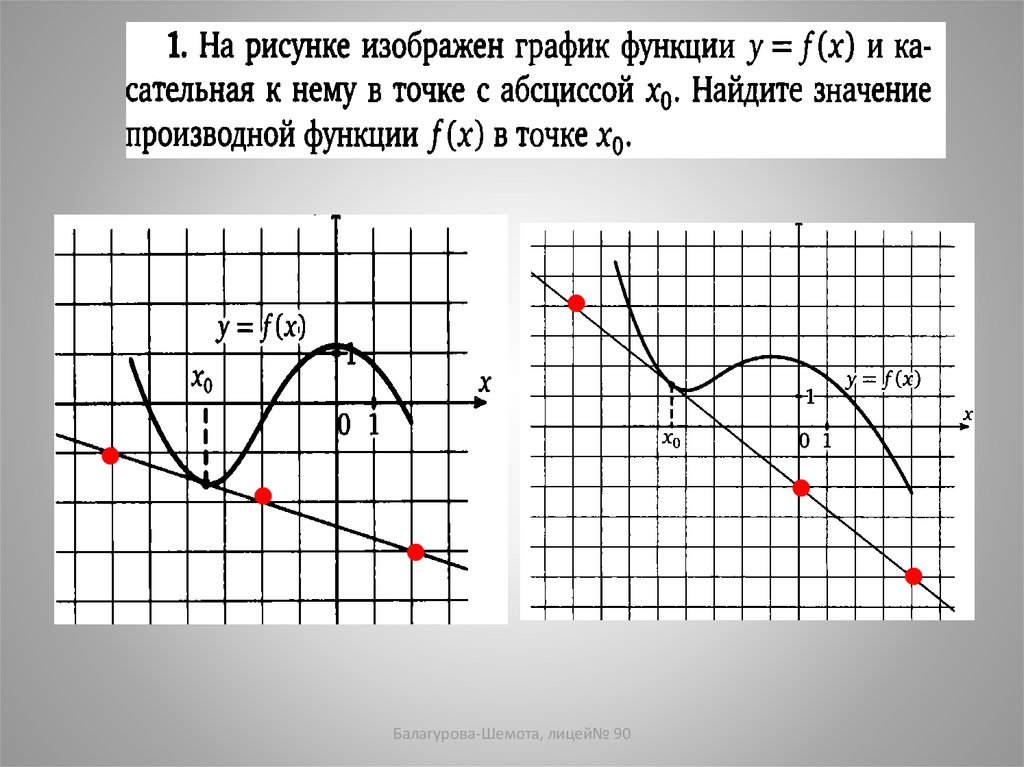
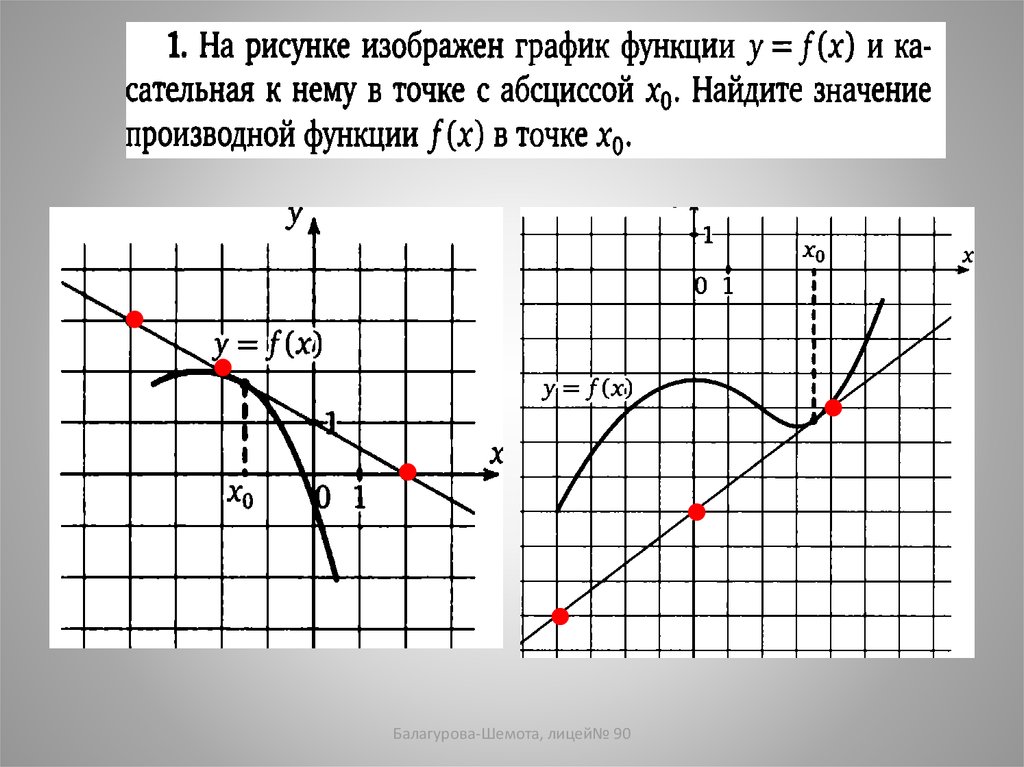
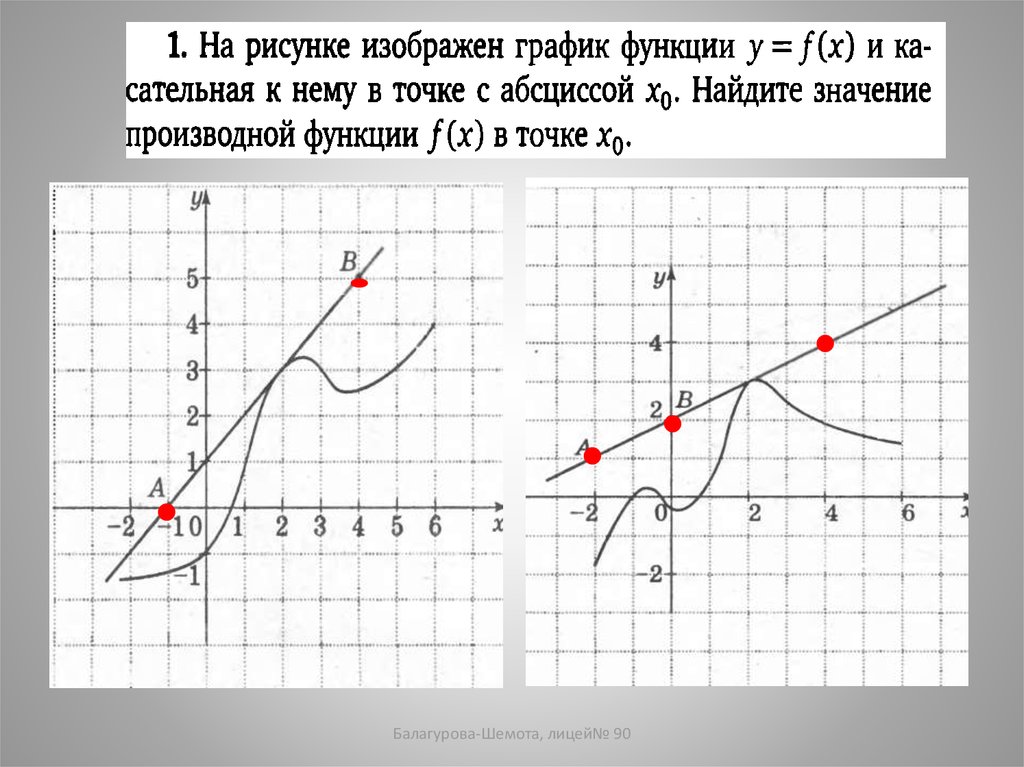
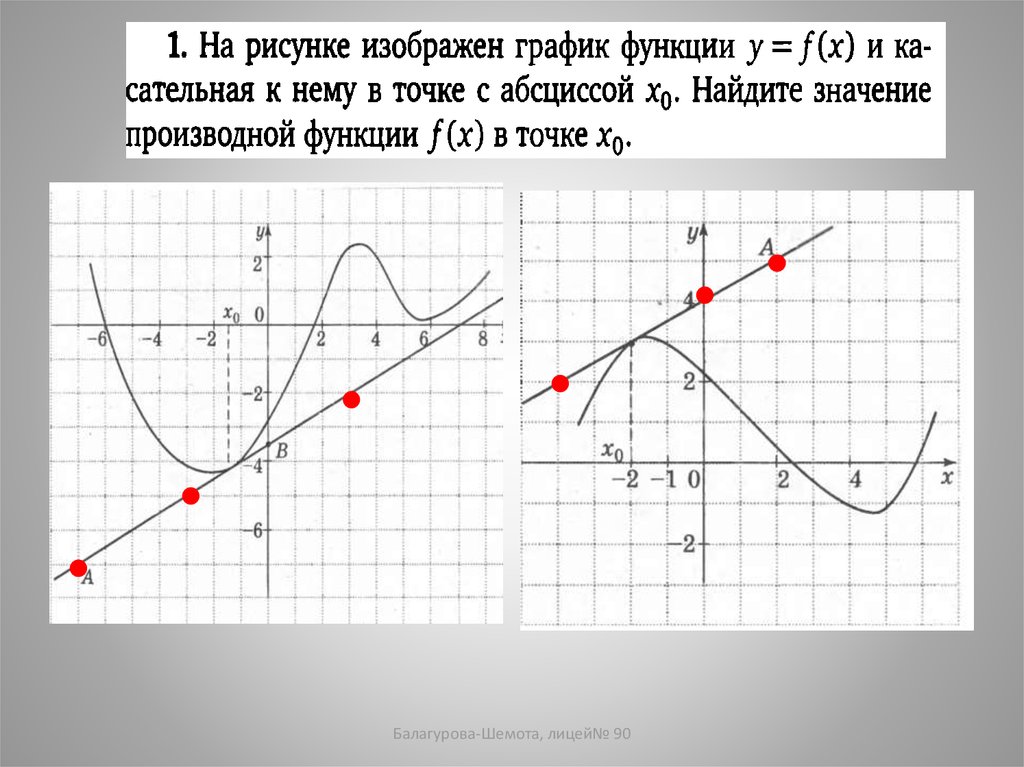
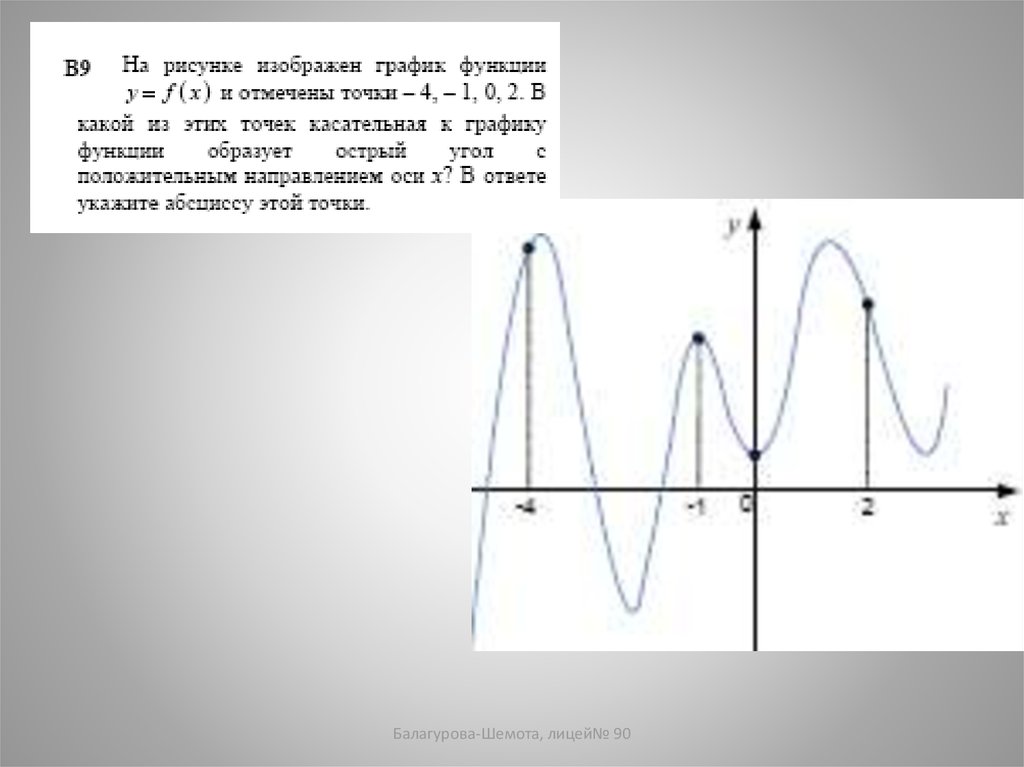
1. На рисунке изображен график функции y=f(x)
и
касательная к нему в точке с абсциссой x0. Найдите
значение производной в точке x0.
a- тупой
y
3
tg α<0 f '(x0)<0
tg α = - tg β
y=f(x)
1
0 1
a
β
2 x0
tg α = - 3/2 =
= - 1,5 = f '(x0)
x
Балагурова-Шемота, лицей№ 90

4.

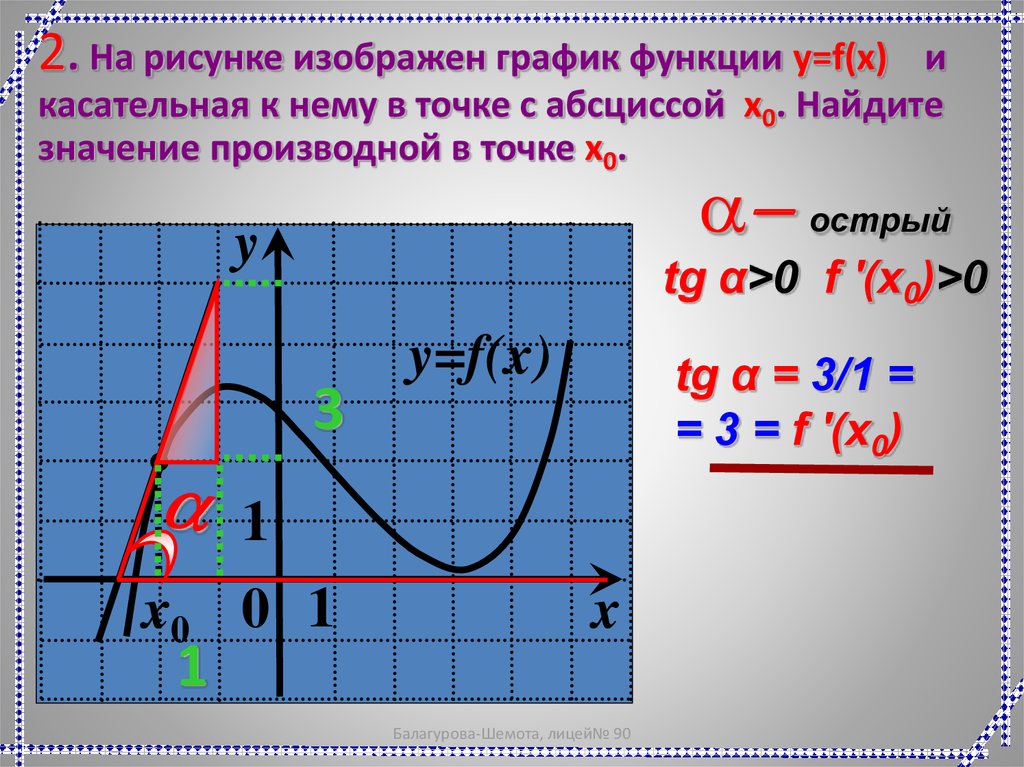
2. На рисунке изображен график функции y=f(x)
и
касательная к нему в точке с абсциссой x0. Найдите
значение производной в точке x0.
a- острый
y
tg α>0 f '(x0)>0
3
y=f(x)
tg α = 3/1 =
= 3 = f '(x0)
1
x0 0 1
1
x
Балагурова-Шемота, лицей№ 90

5.

Балагурова-Шемота, лицей№ 90

6.

Балагурова-Шемота, лицей№ 90

7.

Балагурова-Шемота, лицей№ 90

8.

Балагурова-Шемота, лицей№ 90

9.

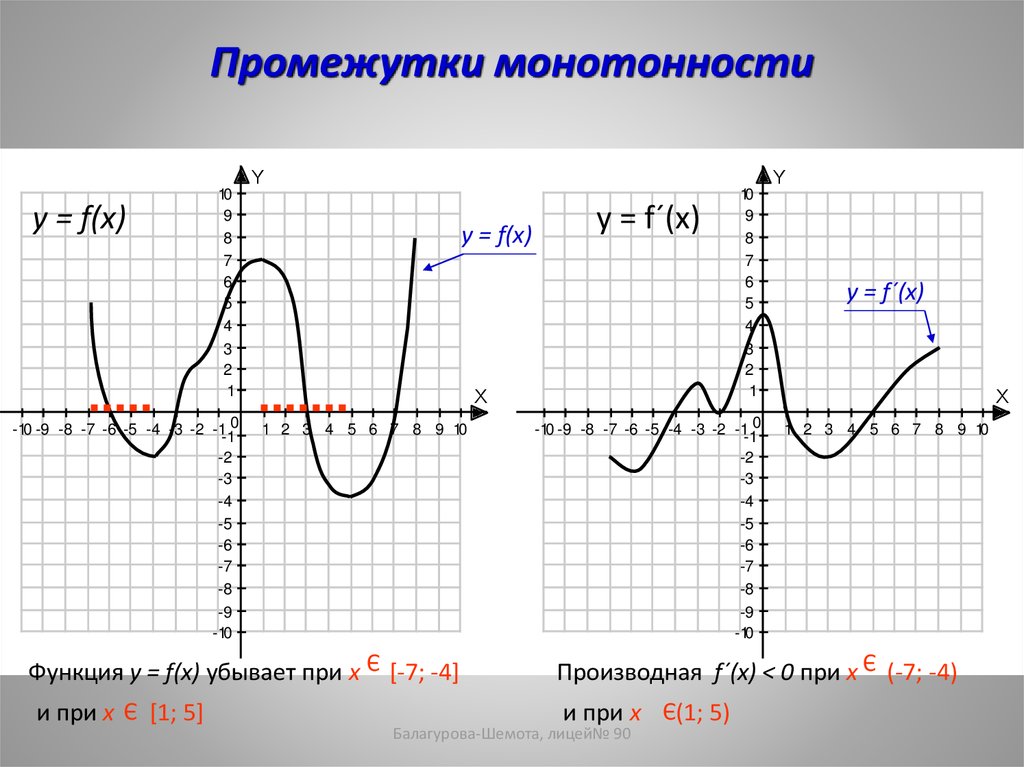
Балагурова-Шемота, лицей№ 90

10. Промежутки монотонности

X
1 2 3 4 5 6 7 8 9 10
Функция y = f(x) убывает при x
Э
и при x
[1; 5]
y = f´(x)
[-7; -4]
10
9
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
y = f´(x)
X
1 2 3 4 5 6 7 8 9 10
Производная f´(x) < 0 при x
и при x
Балагурова-Шемота, лицей№ 90
Э
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
y = f(x)
Э
y = f(x)
Y
(1; 5)
Э
10
9
8
7
6
5
4
3
2
1
(-7; -4)

11.

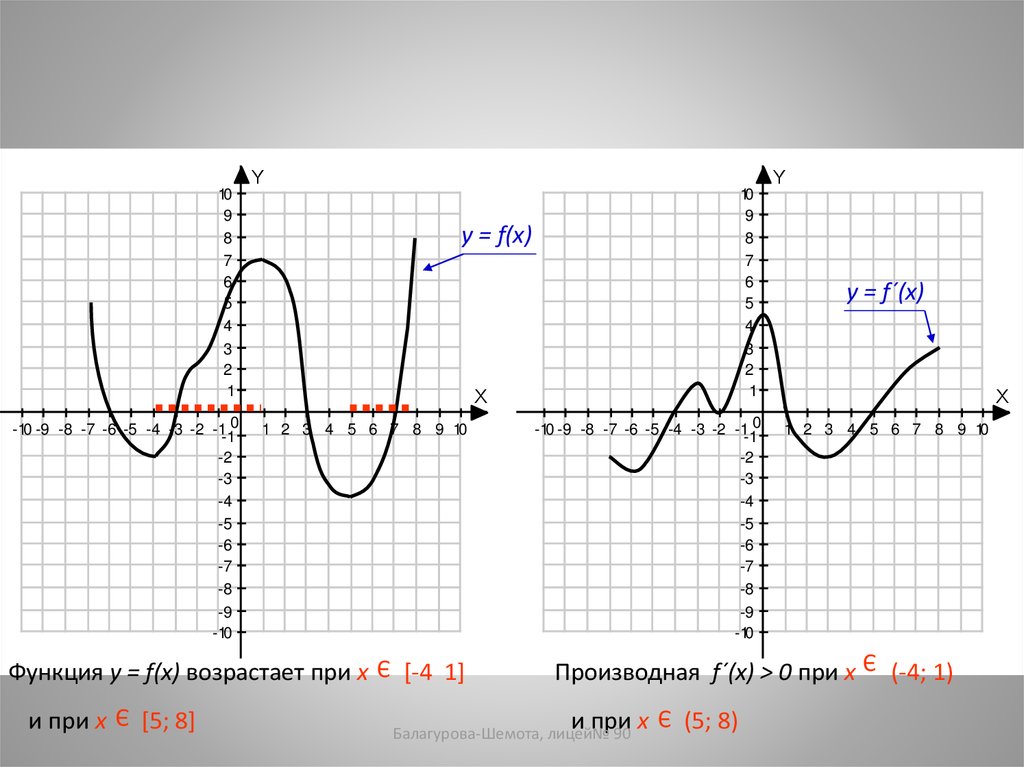
X
[5; 8]
[-4 1]
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
y = f´(x)
X
1 2 3 4 5 6 7 8 9 10
Производная f´(x) > 0 при x
и при x
Балагурова-Шемота, лицей№ 90
Э
1 2 3 4 5 6 7 8 9 10
Функция y = f(x) возрастает при x
Э
и при x
10
9
8
7
6
5
4
3
2
1
y = f(x)
Э
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
(5; 8)
Э
10
9
8
7
6
5
4
3
2
1
(-4; 1)

12.

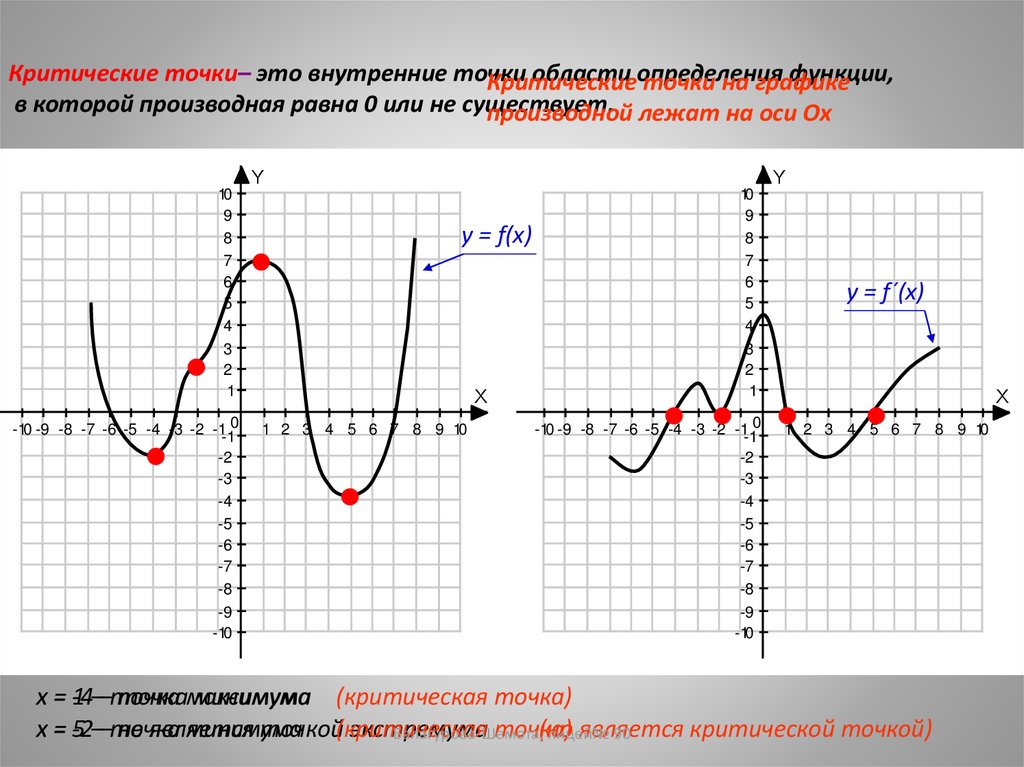
Критические точки– это внутренние точки
области определения
функции,
Критические
точки на графике
в которой производная равна 0 или не существует.
производной лежат на оси Оx
10
9
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
y = f(x)
X
1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
y = f´(x)
X
1 2 3 4 5 6 7 8 9 10
x=1
-4––точка
точкамаксимума
минимума (критическая точка)
x=5
-2––точка
не является
минимума
точкой(критическая
экстремума
точка)
(но
является
критической точкой)
Балагурова-Шемота,
лицей№
90

13.

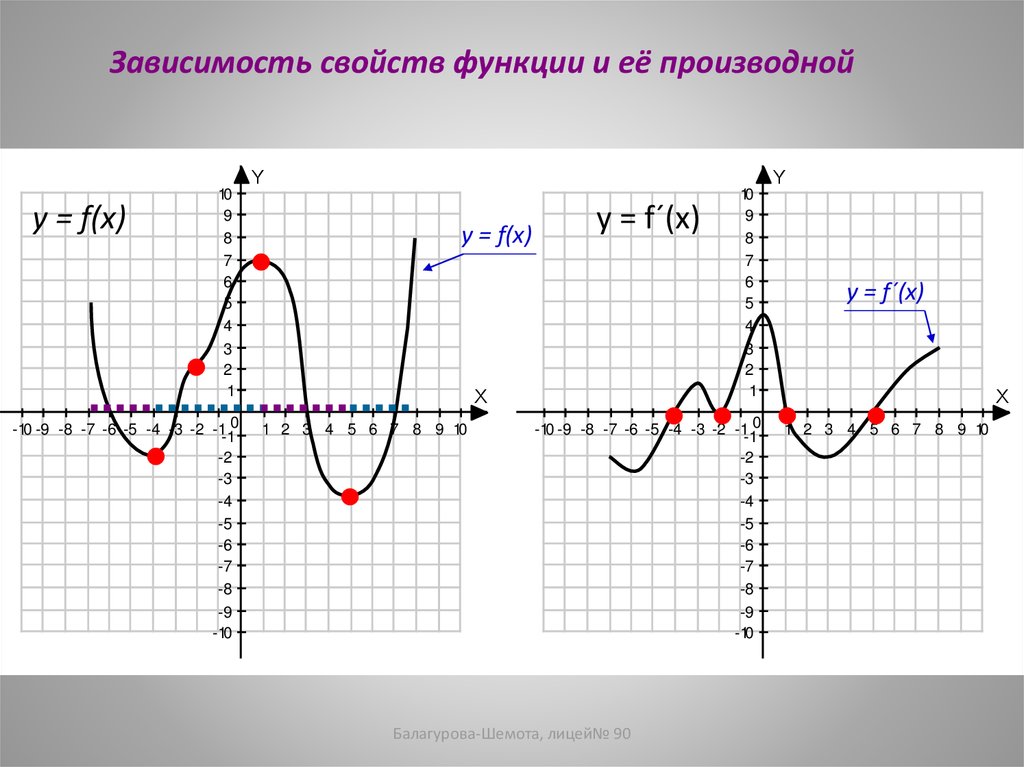
Зависимость свойств функции и её производной
y = f(x)
10
9
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
y = f(x)
y = f´(x)
X
1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-10
-2
-3
-4
-5
-6
-7
-8
-9
-10
Балагурова-Шемота, лицей№ 90
Y
y = f´(x)
X
1 2 3 4 5 6 7 8 9 10

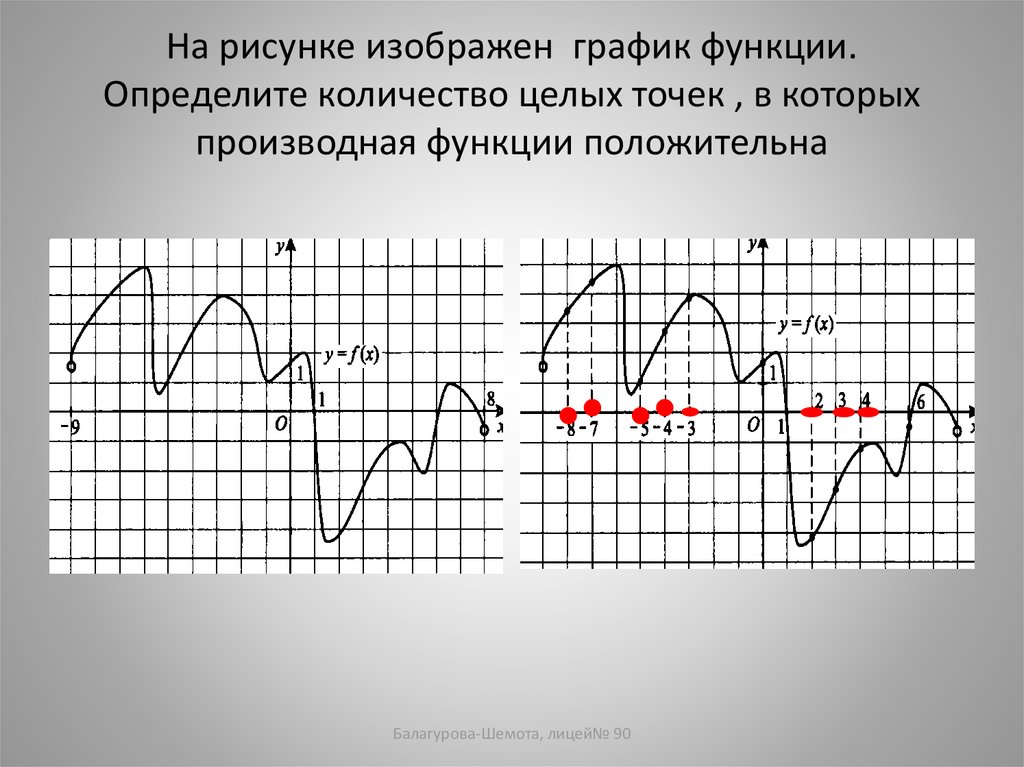
14. На рисунке изображен график функции. Определите количество целых точек , в которых производная функции положительна

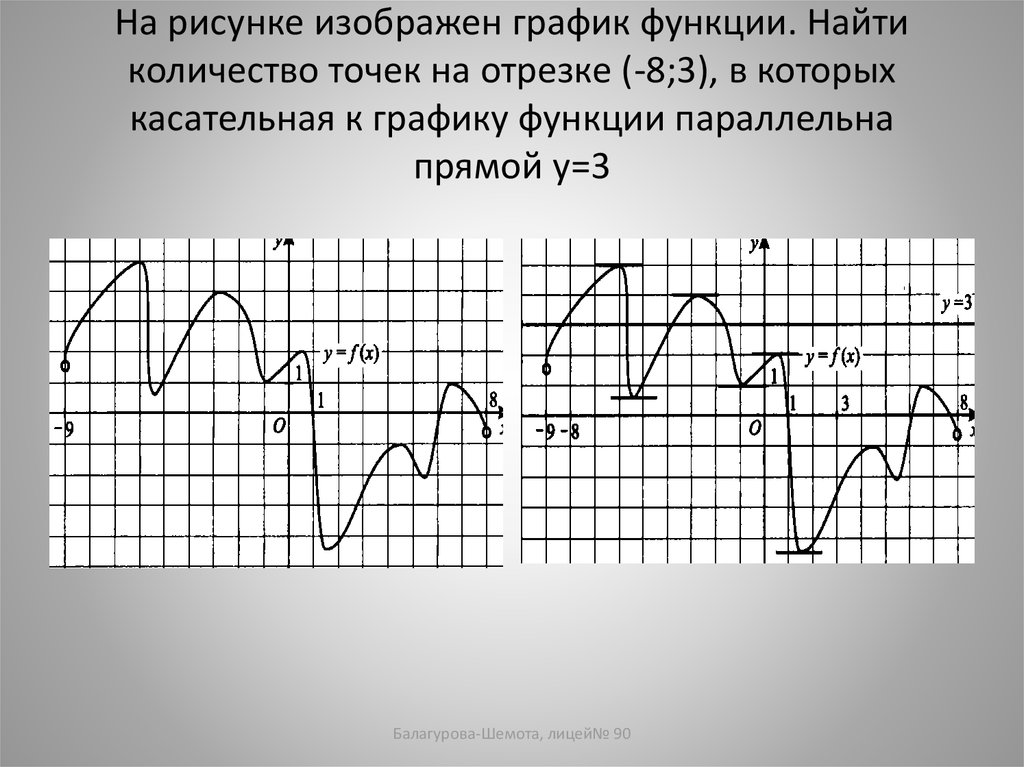
Балагурова-Шемота, лицей№ 90

15. На рисунке изображен график функции. Найти количество точек на отрезке (-8;3), в которых касательная к графику функции

параллельна
прямой у=3
Балагурова-Шемота, лицей№ 90

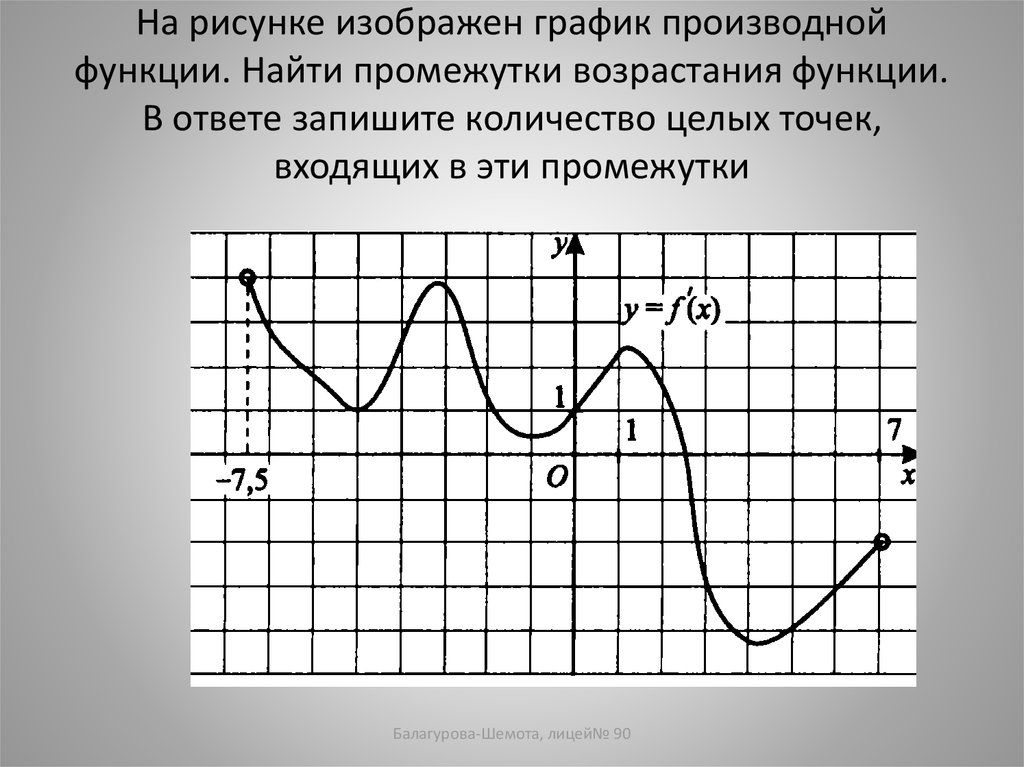
16. На рисунке изображен график производной функции. Найти промежутки возрастания функции. В ответе запишите количество целых

точек,
входящих в эти промежутки
Балагурова-Шемота, лицей№ 90

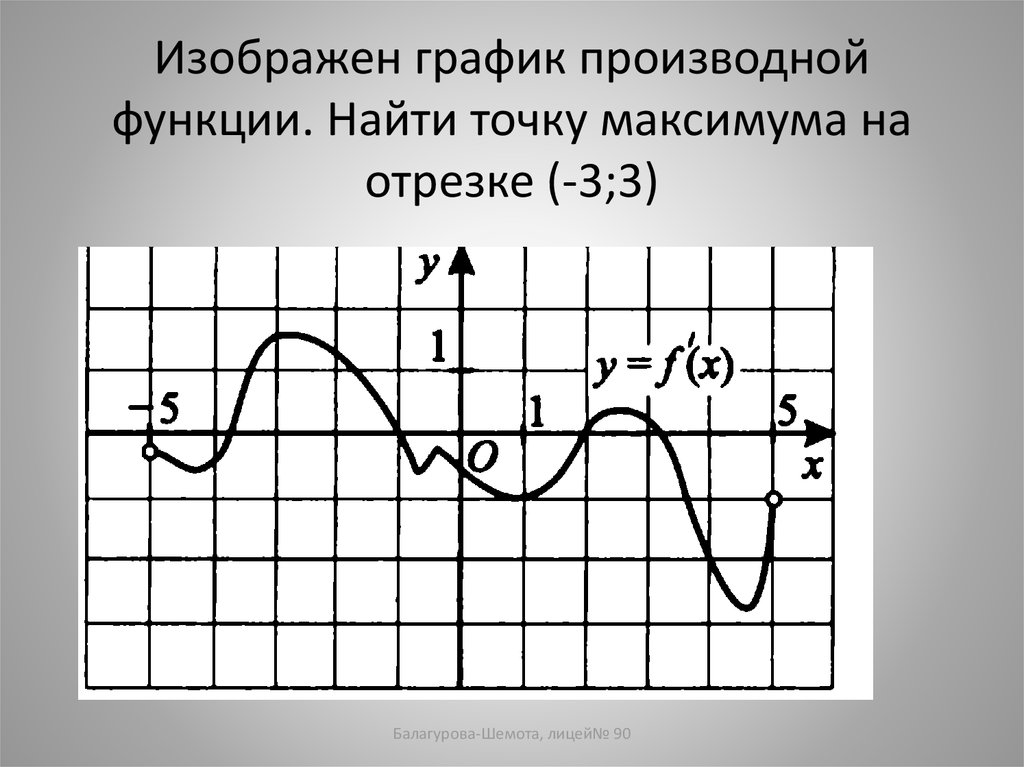
17. Изображен график производной функции. Найти точку максимума на отрезке (-3;3)

Балагурова-Шемота, лицей№ 90

18.

Балагурова-Шемота, лицей№ 90

19.

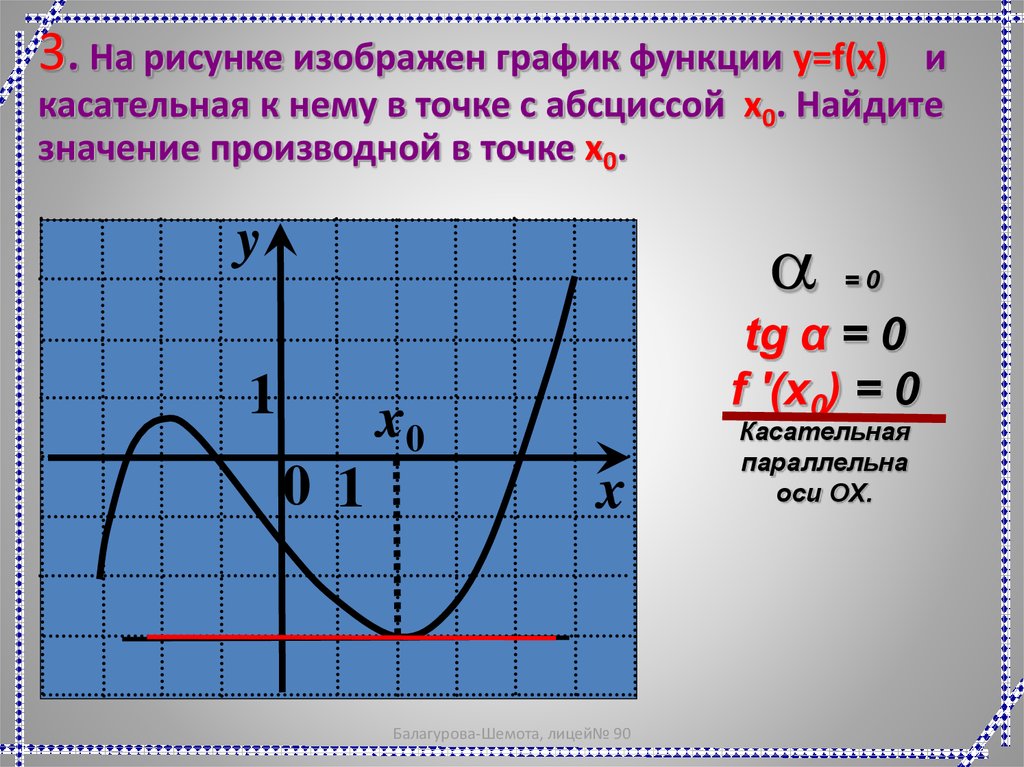
3. На рисунке изображен график функции y=f(x)
и
касательная к нему в точке с абсциссой x0. Найдите
значение производной в точке x0.
a
y
1
tg α = 0
f '(x0) = 0
x0
0 1
=0
x
Балагурова-Шемота, лицей№ 90
Касательная
параллельна
оси ОХ.

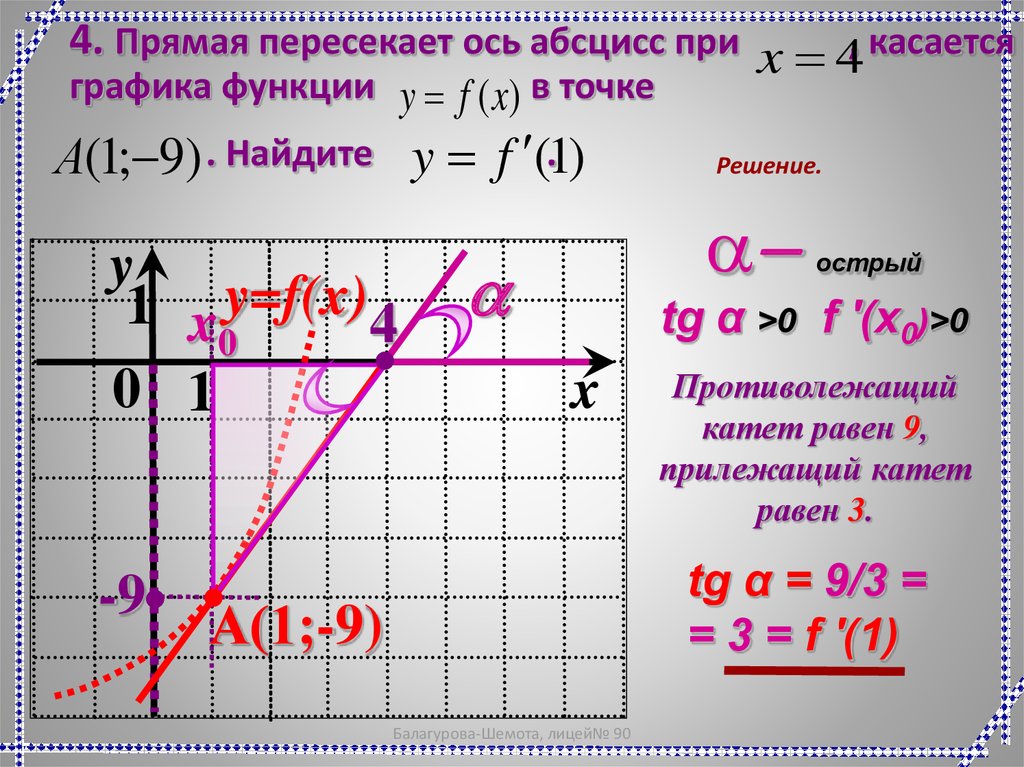
20.

4. Прямая пересекает ось абсцисс при x 4, касается
графика функции y f (x) в точке
А(1;-9) . Найдите y f (.1)
y
1 x y=f(x)4
0
0 1
-9
Решение.
a-
a
острый
tg α >0 f '(x0)>0
x
Противолежащий
катет равен 9,
прилежащий катет
равен 3.
tg α = 9/3 =
= 3 = f '(1)
А(1;-9)
Балагурова-Шемота, лицей№ 90

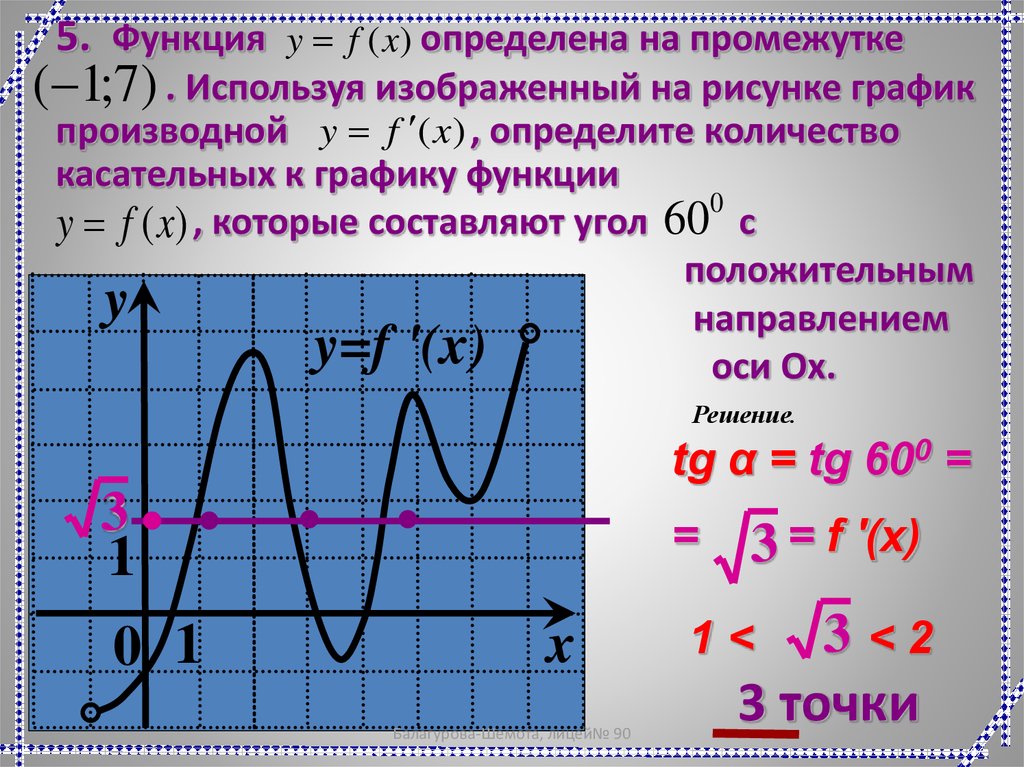
21.

5. Функция y f (x) определена на промежутке
(-1;7) . Используя изображенный на рисунке график
производной y f (x) , определите количество
касательных к графику функции
0
y f (x) , которые составляют угол 60 с
положительным
y
направлением
y=f '(x)
оси Ox.
Решение.
tg α = tg 600 =
3
1
0 1
=
x
Балагурова-Шемота, лицей№ 90
3 = f '(x)
3<2
3 точки
1<

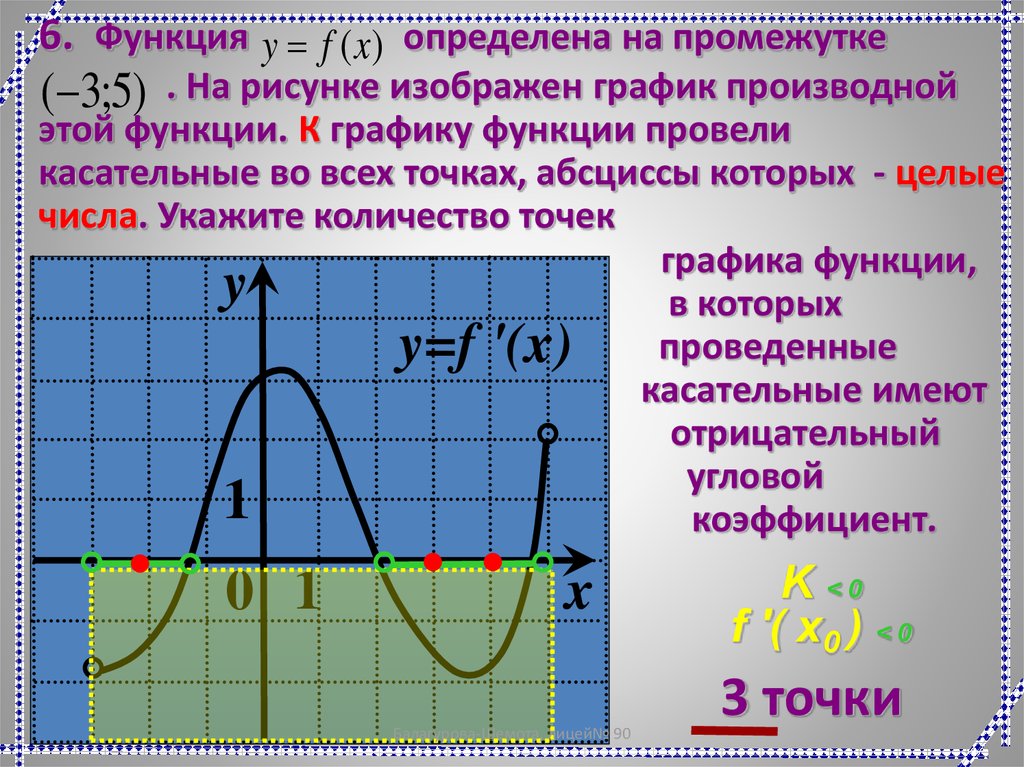
22.

6. Функция y f (x) определена на промежутке
. На рисунке изображен график производной
этой функции. К графику функции провели
касательные во всех точках, абсциссы которых - целые
числа. Укажите количество точек
графика функции,
y
в которых
проведенные
y=f '(x)
касательные имеют
отрицательный
угловой
1
коэффициент.
(-3;5)
0 1
x
Балагурова-Шемота, лицей№ 90
K <0
f '( x0 ) < 0
3 точки

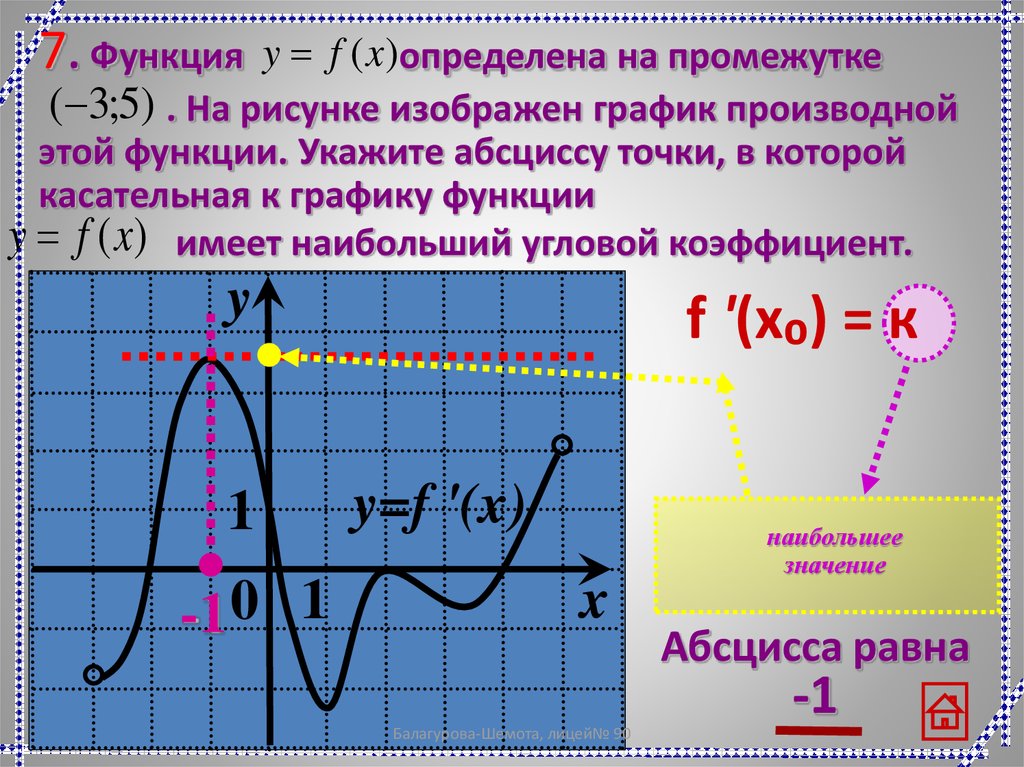
23.

y f (x)определена на промежутке
(-3;5) . На рисунке изображен график производной
этой функции. Укажите абсциссу точки, в которой
касательная к графику функции
y f (x) имеет наибольший угловой коэффициент.
7. Функция
y
1
-1 0 1
f '(x₀) = к
y=f '(x)
наибольшее
значение
x
Балагурова-Шемота, лицей№ 90
Абсцисса равна
-1