Similar presentations:
Ekonometria. Weryfikacja modelu ekonometrycznego
1. Ekonometria
Wykład 7dr hab. Małgorzata Radziukiewicz, prof. PSW Biała Podlaska
2.
3.
4.
5.
6.
7.
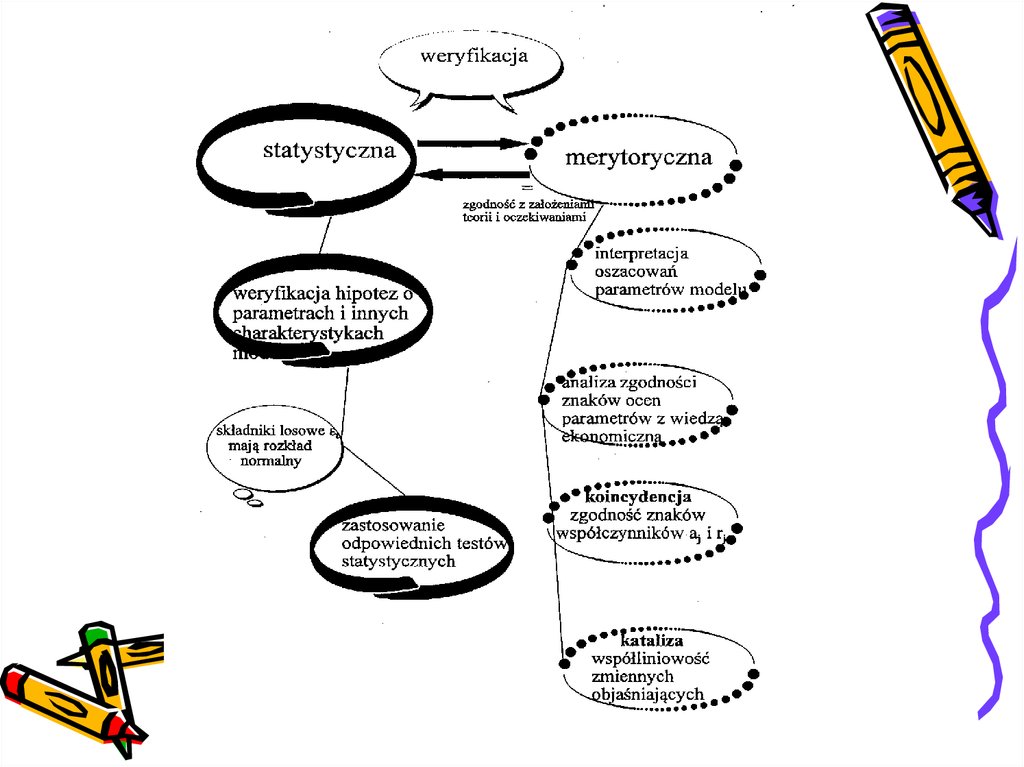
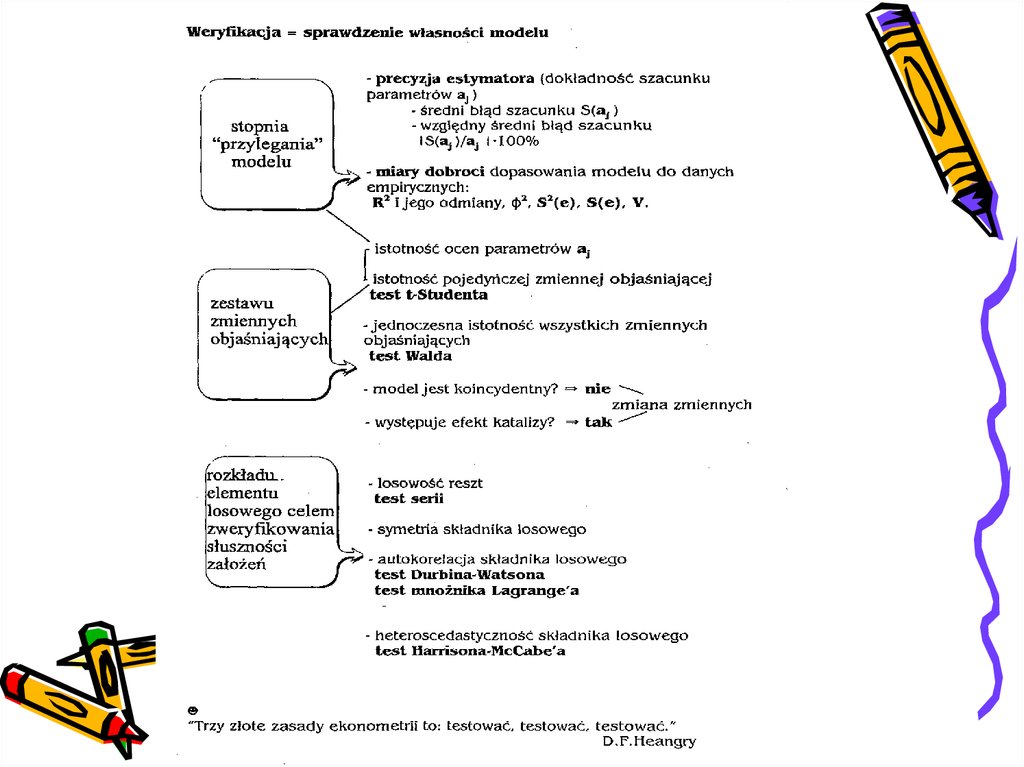
8. Weryfikacja modelu ekonometrycznego
9.
10.
11.
12.
13. Przykład.
• Do modelu wybrano zmienne objaśniające X1 orazX2.
• Macierz obserwacji na zmiennych objaśniających
modelu jest postaci:
• Wektor wartości zmiennej objaśnianej Y:
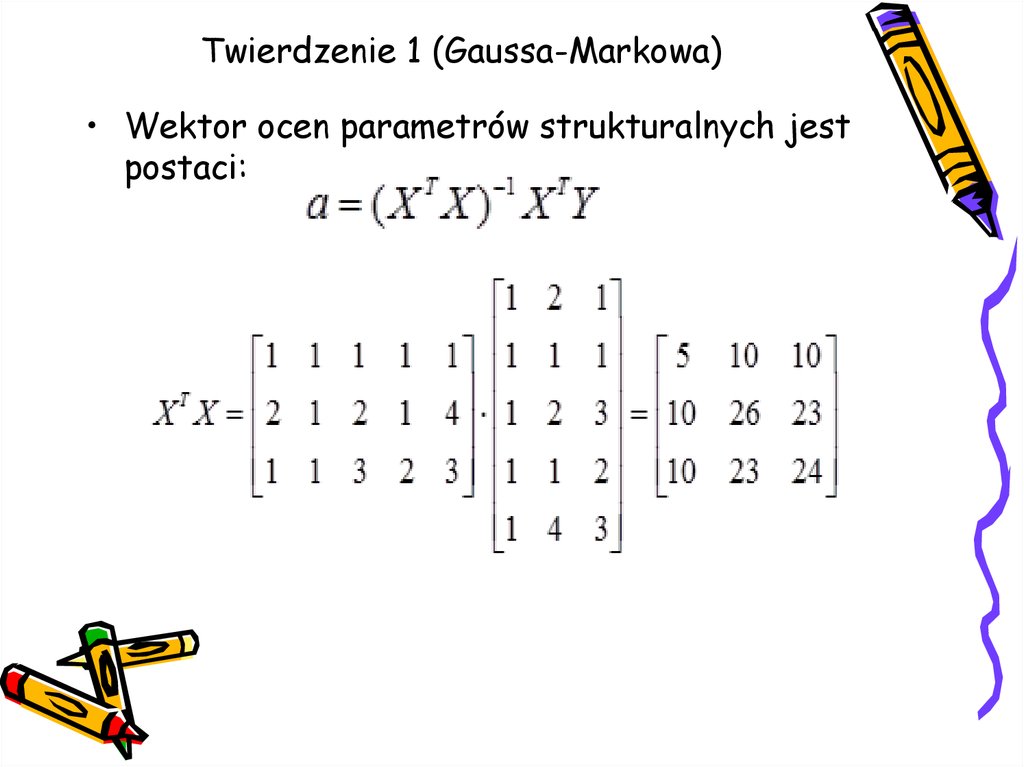
14. Twierdzenie 1 (Gaussa-Markowa)
• Wektor ocen parametrów strukturalnych jestpostaci:
15.
• Macierz odwrotna do macierzy XTX16.
• Obliczamy wartości ocen parametrówstrukturalnych modelu ekonometrycznego:
• Model ekonometryczny jest postaci:
17.
• Interpretacja:• a0 = 7,941 to średnia wartość Y w przypadku, gdy
zmienne objaśniające X1 i X2 są równe 0;
• a1 = 1,341 oznacza o ile przeciętnie wzrośnie Y,
jeżeli zmienna objaśniająca X1 wzrośnie o
jednostkę, podczas gdy zmienna objaśniająca X2
pozostanie bez zmian;
• a2 = 1,800 oznacza, o ile przeciętnie wzrośnie Y,
jeżeli zmienna objaśniająca X2 wzrośnie o
jednostkę, podczas gdy zmienna objaśniająca X1
pozostanie bez zmian.
18.
19.
20. Twierdzenie 2 (Gaussa-Markowa)
• Wariancja składnika resztowego (estymatorwariancji składnika losowego) według wzoru:
T
e e
S (e)
n (k 1)
2
• Do obliczenia wariancji potrzebne są reszty:
• gdzie:
- wartości teoretyczne zmiennej obajśnianej (uzyskane
na podstawie modelu) = wartości przewidywane
- wartości zmiennej objaśnianej (empiryczne )
21. Ile wynoszą reszty?
• Do oszacowanego modelu:• podstawiamy kolejne wartości zmiennych X1 i X2
12,423
11,082
Yˆ 16,023
12,882
18,705
22.
• Wektor reszte1 12,423 10 2,423
e2 11,082 12 0,918
e3 16,023 13 3,023
e4 12,882 15 2,118
e5 18,705 20 1,295
równa się:
2,423
0,918
e 3,023
2,118
1,295
23.
• licznik wzoru to:22,014
22,014
S (e)
11,007
n (k 1)
2
2
24.
• Odchylenie standardowe składnikaresztowego (błąd estymacji):
S (e) S 2 (e) 11,007 3,318
• Interpretacja:
• Poszczególne obserwacje empiryczne Y
odchylają się średnio od teoretycznych o ±
3,318 jednostek.
25. Twierdzenie 3 (Gaussa-Markowa
• Wariancja estymatora parametrówstrukturalnych według wzoru:
wynosi:
Obliczając wartości elementów diagonalnych
macierzy D2(a) otrzymamy oceny wariancji
poszczególnych parametrów modelu
26. Wnioskowanie o dokładności szacunku parametrów αi
• Błędy średnie szacunku parametrówstrukturalnych:
S (a0 ) 11,007 1,267 13,946 3,734 3,7
S (a1 ) 11,007 0,267 2,939 1,714 1,7
S (a2 ) 11,007 0,400 4,403 2,098 2,1
• Interpretacja:
O ile +- odchylają się wartości ocen
parametrów strukturalnych od ich
wartości rzeczywistych
27.
• Do interpretacji lepiej posługiwać sięśrednimi względnymi błędami szacunku
parametrów wyznaczonymi ze wzoru:
S (a0 )
3,734
100%
100% 47,02%
a0
7,941
S (a1 )
1,714
100%
100% 127,82%
a1
1,341
S (a 2 )
2,089
100%
100% 116,06%
a2
1,800
Błędy średnie stanowią odpowiednio 47,02%, 127,82% oraz
116,06% wartości kolejnych parametrów.
28. Współczynnik zbieżności dany wzorem:
wynosi:bowiem:
29.
• Współczynnik zbieżności φ2 = 0,380oznacza, iż 38% zmienności zmiennej
objaśnianej Y nie zostało wyjaśnione przez
model.
• Współczynnik determinacji R2 :
R 1 1 0,380 0,620
2
2
co oznacza, iż 62% zmienności zmiennej
objaśnianej Y zostało wyjaśnione przez
model
30.
• Współczynnik zmienności losowej:• Interpretacja:
• Odchylenia losowe stanowią 23,7%
wartości średniej zmiennej objaśnianej Y.
31.
• W ekonometrii przyjęta jest konwencjapodawania średnich błędów szacunku
parametrów strukturalnych łącznie z
oszacowaniem modelu.
• Oszacowany model ekonometryczny jest
postaci:
32.
33. Weryfikujemy istotność parametrów strukturalnych oszacowanego modelu
• Stawiamy hipotezę:• H0: αi = 0 (parametr αi nieistotnie różni się od
zera tzn. że zmienna Xi przy której parametr stoi
wywiera nieistotny wpływ na zmienną objaśnianą );
• H1: αi ≠ 0 (parametr αi istotnie różni się od zera);
• Test istotności pozwalający na weryfikację
hipotezy H0: αi = 0 oparty jest na rozkładzie
statystyki t-Studenta określonej wzorem:
34.
• Dla każdego parametru obliczamy wartościempiryczne statystyki t:
7,941
2,127
3,734
1,341
0,782
1,714
1,800
0,862.
2,089
t ( a0 )
t ( a1 )
t ( a2 )
• Z tablic t-Studenta dla przyjętego poziomu
istotności α = 0,01 oraz dla n-(k+1)= 5–(2+1)=2
stopnie swobody odczytujemy wartość krytyczną
t* = 4,303.
35.
• Jeżeli spełniona jest nierówność:to hipoezę H0 należy odrzucić na
korzyśćalternatywnej hipotezy H1, czyli
dany parametr jest statystycznie istotny.
• W przypadku, gdy:
nie ma odstaw do odrzucenia hipotezy
H0 o nieistotności parametru.
36.
• Z naszych obliczeń wynika m.in., iż:więc hipotezę H1 odrzucamy, a parametr a0 jest
statystycznie nieistotny.
• Dla parametrów a1 i a2 spełniona jest również
nierówność:
co oznacza, iż w tym przypadku również nie ma
podstaw do odrzucenia hipotezy H0.
• Interpretacja:
Parametry a0, a0 i a2 są statystycznie nieistotne. A
zatem zmienne objaśniające X1 i X2 wywierają
nieistotny wpływ na zmienną objaśnianą Y.
37.
38. Badanie koincydencji
• Model jest koincydentny, jeżeli dla każdejzmiennej objaśniającej model zachodzi:
gdzie:
• ai – jest oceną parametru strukturalnego αi;
• ri – jest współczynnikiem korelacji między zmienną
Y a zmienną Xi.
Model jest koincydentny.
39. Współliniowość – czy zmienne są katalizatorami?
• Zmienna Xi z pary zmiennych ( Xi, Xj) jestkatalizatorem jeżeli:
ri
rij 0
lub
rij
rj
• Z obliczeń wynika, iż:
Żadna ze zmiennych nie jest katalizatorem.
40.
41. Badanie losowości
• Badanie losowości ma związek z wyborem postacianalitycznej modelu.
• W standardowym modelu liniowym zmienna
objaśniana jest liniową funkcją zmiennych
objaśniających plus korekta.
• W przypadku, gdy korekty mają przez dłuższy
okres jednakowe znaki można przypuszczać, że
został popełniony błąd specyfikacji:
– nietrafny wybór postaci analitycznej modelu;
– nietrafny wybór zmiennych objaśniających
42.
43. Czy reszty są losowe?
Wektor reszt2,423
0,918
e 3,023
2
,
118
1,295
Reguły testu (dla prób małych (n≤30)
• Przypisujemy resztom ek symbole a, gdy ek > 0,
oraz b gdy ek <0
• Otrzymujemy ciąg złożony z symboli a i b
• a, b, a, b, b.
• Określamy liczbę serii kemp
kemp = 4
Z tablic liczby serii dla n1 = liczba symboli a i n2 =
liczba symboli b oraz przyjętego α = 0,05
odczytujemy wartośc tα = 2
Wobec kemp > kα nie ma podstaw do odrzucenia
hipotezy, że rozkłsd reszt jest losowy
44. Wartości krytyczne testu serii
45.
46. Czy rozkład reszt modelu jest symetryczny?
W celu zweryfikowaniahipotezy
Z tablic testu t Studenta
• przyjęto poziom istotności
• dla przyjętego poziomu
testu a = 0,05:
istotności α oraz dla n-1
• m = 2 - liczba reszt dodatnich
stopni swobody
• n = 5 – całkowita liczba reszt
odczytuje się wartość
• następnie obliczono wartość
krytyczną t*
statystyki testowej temp = 1,67
• Dla n-1=5-1=4 stopni swobody • . Jeżeli |temp|≤t*, nie ma
podstaw do odrzucenia
wartość t*= 2,776.
hipotezy H0 i rozkład
reszt modelu jest
• Odp. Rozkład reszt jest
losowy, bowiem 1,67<2,776
symetryczny.
47. Czy występuje autokorelacja skladnika losowego?
• Jednym z założeń dotyczących modelu regresjijest niezależność błędów obserwacji, czyli fakt,
czy występujące reszty w predykcji zmiennej
zależnej są ze sobą skorelowane.
• Dobrze dopasowane modele regresji zakładają, że
otrzymywane reszty (e) - błędy przewidywania
rzeczywistej wartości zmiennej zależnej na
podstawie utworzonego przez nas modelu regresji
- są niezależne od siebie,
• Oznacza to, że rozkład reszt jest losowy,
przypadkowy, bez stale występującego wzorca.
48.
• Sposobem określenia niezależnościbłędów obserwacji jest wyznaczenie
autokorelacji składnika resztowego,
czyli korelacji r-Pearsona pomiędzy
kolejnymi resztami, powstałymi z
nieidealnego dopasowania modelu.
cov( t , t i )
i
D( t ) D( t i )
zależność korelacyjna składników losowych εt oraz
ich pierwszych opóźnień εt-i
49. Współczynnik korelacji Pearsona
• rxy jest miernikiem związkuliniowego między dwiema
cechami (zmiennymi)
mierzalnymi
• jest wyznaczany poprzez
standaryzację kowariancji
• kowariancja (wariancja
wspólna cech x i y) jest średnią
arytmetyczną iloczynu odchyleń
wartości liczbowych tych cech
(zmiennych) x i y od ich
średnich arytmetycznych
n
rxy
( x x)( y y )
i 1
i
i
n S ( x) S ( y )
cov( x, y )
rxy
S ( x) S ( y )
1 n
cov( x, y ) cov( y, x) ( xi x )( yi y ) x y x y
n i 1
50. Proces autokorelacji rzędu I
• Załóżmy, że składniki losowe εt związane sązależnością:
t t 1 t
1
gdzie:
(t=1...,n-1)
zmienne losowe η są niezależne i mają jednakowy rozkład
51. Test Durbina-Watsona
• Test Durbina-Watsona (statystyka) służy dooceny występowania korelacji pomiędzy
resztami (błędami, składnikami resztowymi).
• Sprawdzamy, czy składniki losowe modelu
pochodzą z procesu autokorelacji rzędu I.
• Przyczyną występowania zjawiska autokorelacji
składnika losowego w modelu są:
– natura procesów ekonomicznych (skutki pewnych
zdarzeń albo decyzji rozciągaja sie na wiele
okresów;
– niepoprawna postać analityczna modelu;
– niepełny zestaw zmiennych objasniających.
52.
53. Tablice testu Durbina-Watsona prezentują wartości krytyczne dL oraz dU dla odpowiedniej liczby obserwacji n oraz liczby
Tablice testu Durbina-Watsona prezentują wartości krytyczne dL oraz dU dlaodpowiedniej liczby obserwacji n oraz liczby zmiennych objaśniających k
54. Czy występuje autokorelacja reszt?
Statystyka d• Dla modelu wartość:
n
d
2
(
e
e
)
t t 1
t 2
n
2
(
e
)
t
t 1
• d= 53,501/22,015=2,430
Obliczenia:
55.
• Zasadą jest, że wartości statystyktestowych w zakresie od 1,5 do 2,5 są
stosunkowo normalne.
• Każda wartość spoza tego zakresu może
być powodem do obaw.
• Statystyka Durbina – Watsona, chociaż
wyświetlana przez wiele programów analizy
regresji, nie ma zastosowania w niektórych
sytuacjach.
• Np. gdy opóźnione zmienne zależne są
zawarte w zmiennych objaśniających,
niewłaściwe jest użycie tego testu.



















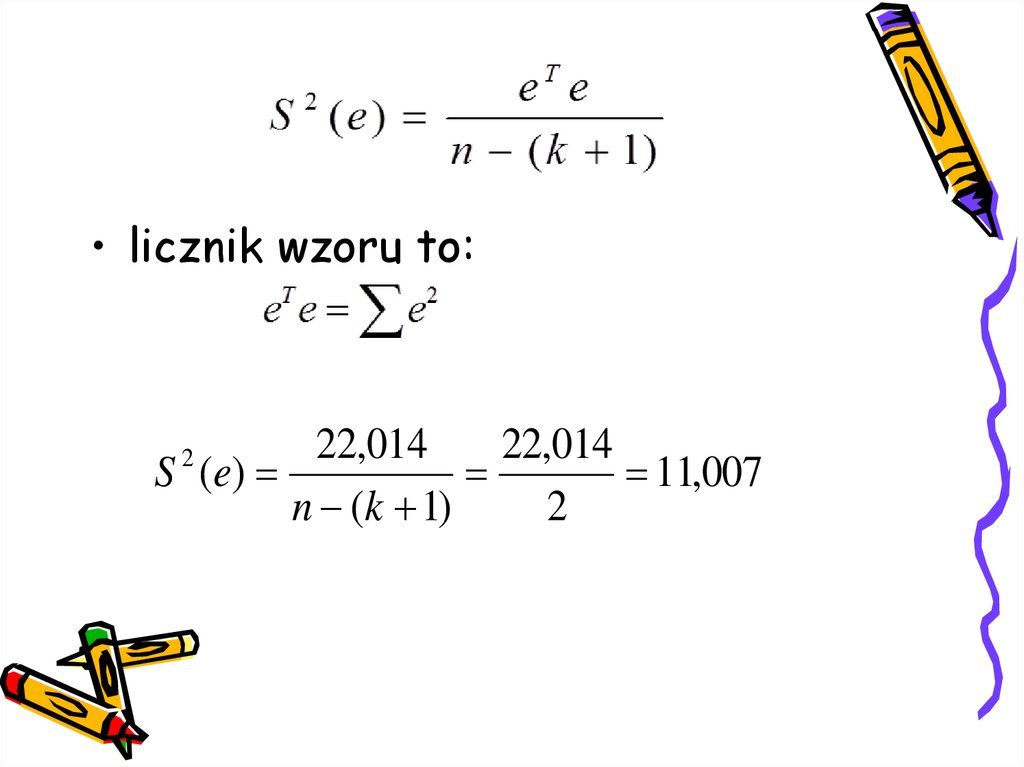




































 economics
economics








