Similar presentations:
Параллельные вычислительные процессы
1. Параллельные вычислительные процессы
1Романенко Владимир Васильевич,
к.т.н., доцент каф. АСУ ТУСУР
2. Параллельные вычислительные процессы
2ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНЫХ
ПРОЦЕССОВ
3. Базовые определения
3Имена процессов будем обозначать словами,
составленными из прописных букв, а буквами P, Q, R,
… будем обозначать произвольные процессы.
Буквы x, y, z, … используются для переменных,
обозначающих события.
Буквы A, B, C, … используются для обозначения
множества событий.
Буквы X, Y, Z, … используются для переменных,
обозначающих процессы.
Алфавит процесса P обозначается αP.
Процесс с алфавитом αP, такой, что в нем не
происходит ни одно событие из αP, назовем СТОПαP.
4. Базовые определения
4Пример: автомат, торгующий шоколадками.
В качестве имени процесса выберем ТАП
(торговый аппарат простой).
Имена событий – мон (опускание монеты в щель
автомата) и шок (появление шоколадки из
выдающего устройства).
Алфавит αТАП = {мон, шок}.
5. Префиксная запись
5Префиксная форма описания процессов:
(x → P),
где
x – событие;
P – процесс.
При этом
α(x → P) = αP, x αP.
Пример:
(мон → (шок → (мон → (шок → СТОПαТАП)))).
6. Рекурсивная запись
6Рекурсивный метод определения процесса:
P = (x → P),
P = (x → (y → P)),
и т.д. Здесь x, y αP.
Пример 1:
ТАП = (мон → (шок → ТАП)).
7. Рекурсивная запись
7Рекурсивный метод определения процесса:
P = (x → P),
P = (x → (y → P)),
и т.д. Здесь x, y αP.
Пример 2: процесс ЧАСЫ описывает часы,
единственная функция которых – тикать:
αЧАСЫ = {тик},
ЧАСЫ = (тик → ЧАСЫ).
8. Определение выбора
8Описание объектов с несколькими линиями
поведения:
(x → P | y → Q),
где
α(x → P | y → Q) = αP, x, y αP, αP = αQ.
Пример 2: копирование битов из входного канала в
выходной:
αКОПИБИТ = {вв.0, вв.1, выв.0, выв.1},
КОПИБИТ = ((вв.0 → выв.0 | вв.1 → выв.1) →
КОПИБИТ).
9. Параллельные процессы
9Оператор параллельной композиции:
P || Q.
Законы:
P || Q = Q || P – логическая симметрия между
процессом и его окружением;
(c → P) || (c → Q) = c → (P || Q),
(c → P) || (d → Q) = СТОП – пара процессов с
одинаковыми алфавитами либо одновременно
выполняет одно и то же действие, либо попадает
в состояние тупика, если начальные события
процессов не совпадают;
10. Параллельные процессы
10Оператор параллельной композиции:
P || Q.
Законы:
P || (Q || R) = (P || Q) || R – ассоциативность (при
совместной работе процессов неважно, в каком
порядке они объединены оператором
параллельной композиции);
P || СТОПαP = СТОПαP – процесс, находящийся в
тупиковой ситуации, приводит к тупику всей
системы.
11. Задача об обедающих философах
11Алфавит философа:
αФИЛi = {i.садится, i.встает, i.берет_вил.i,
i.берет_вил.(i+51),
i.кладет_вил.i, i.кладет_вил.(i+51)}
Алфавит вилки:
αВИЛi = {i.берет_вил.i, (i–51).берет_вил.i,
i.кладет_вил.i, (i–51).кладет_вил.i}
12. Задача об обедающих философах
12Поведение философа:
ФИЛi = (i.садится → i.берет_вил.i →
i.берет_вил.(i+51) →
i.кладет_вил.i → i.кладет_вил.(i+51) →
i.встает → ФИЛi)
Поведение вилки:
ВИЛi = (i.берет_вил.i → i.кладет_вил.i → ВИЛi |
(i–51).берет_вил.i → (i–51).кладет_вил.i →
ВИЛi)
13. Задача об обедающих философах
13Поведение всего пансиона:
ФИЛОСОФЫ =
(ФИЛ0 || ФИЛ1 || ФИЛ2 || ФИЛ3 || ФИЛ4),
ВИЛКИ =
(ВИЛ0 || ВИЛ1 || ВИЛ2 || ВИЛ3 || ВИЛ4),
ПАНСИОН = (ФИЛОСОФЫ || ВИЛКИ)
14. Протоколы поведения процессов
14Протоколом поведения процесса
называется конечная последовательность
символов, фиксирующая события, в которых
процесс участвовал до некоторого момента
времени.
Примеры:
– пустой протокол;
x – протокол из одного события;
x, y – протокол из двух событий и т.д.
мон, шок, мон , мон, шок, мон, шок .
15. Операции с протоколами
15Конкатенация:
s^t,
tn+1 = t^tn,
(s^t)n+1 = s^(s^t)n^t.
Например:
мон, шок ^ мон = мон, шок, мон .
Свойства:
s^(t^u) = (s^t)^u – ассоциативность;
s^ = ^s = s – пустой протокол служит
единицей.
16. Операции с протоколами
16Сужение:
t ↑ A.
Например:
мон, шок, мон ↑ мон = мон, мон .
Свойства:
x ↑ A = x , если x A, y ↑ A = , если y A;
(s^t) ↑ A = (s ↑ A)^(t ↑ A) – дистрибутивность;
↑ A = , s ↑ = , (s ↑ A) ↑ B = s ↑ (A B).
17. Операции с протоколами
17Голова и хвост:
s0 – первый элемент;
s′ – результат, полученный после его удаления,
т.е. x, y 0 = x, x, y ′ = y .
Например:
мон, шок, мон 0 = мон,
мон, шок, мон ′ = шок, мон .
18. Параллельные вычислительные процессы
18СЕТИ ПЕТРИ
19. Основные определения
19Сеть Петри N является четверкой N = (P, T, I, O), где:
P = {p1, p2, …, pn} – конечное множество позиций,
n ≥ 0;
T = {t1, t2, …, tm} – конечное множество переходов,
m ≥ 0;
I: T → P* – входная функция, сопоставляющая
переходу мультимножество его входных позиций;
O: T → P* – выходная функция, сопоставляющая
переходу мультимножество его выходных позиций.
20. Основные определения
20Граф сети Петри обладает двумя типами узлов:
кружок, представляющий позицию сети Петри;
и планка, представляющая переход сети Петри.
Маркировка μ – функция отображения
μ: P → Nat,
μ = μ(p1), μ(p2), …, μ(pn) ,
где n – число позиций в сети Петри и μ(pi) Nat,
1 ≤ i ≤ n – количество фишек в позиции pi.
21. Основные определения
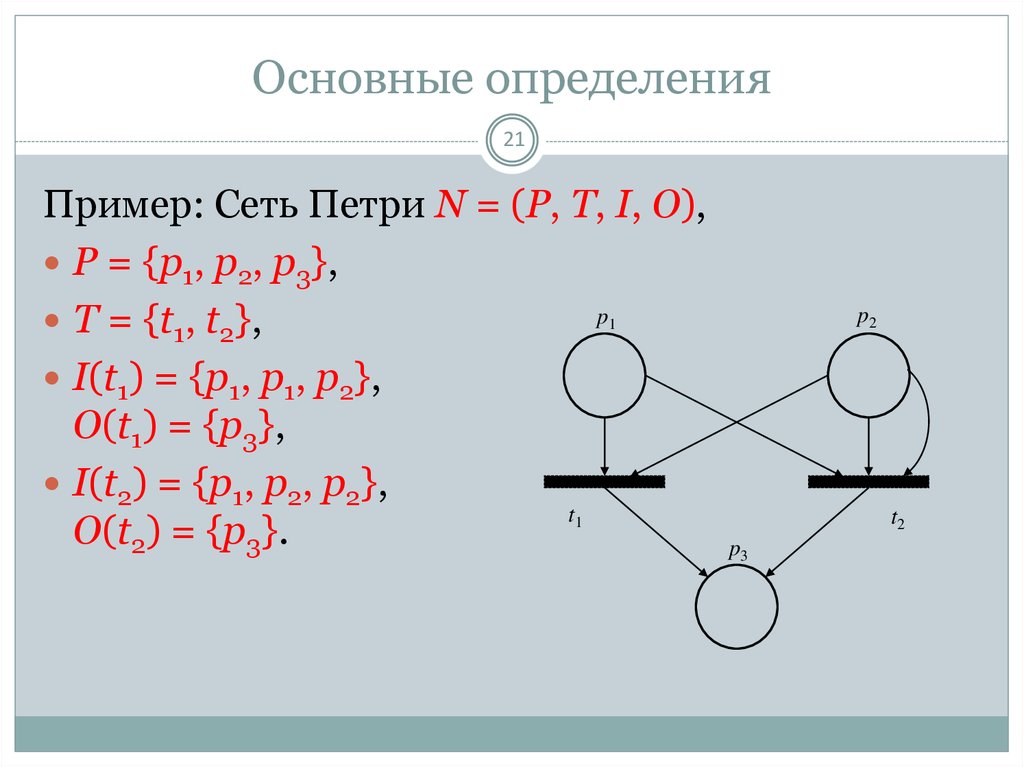
21Пример: Сеть Петри N = (P, T, I, O),
P = {p1, p2, p3},
p
T = {t1, t2},
I(t1) = {p1, p1, p2},
O(t1) = {p3},
I(t2) = {p1, p2, p2},
t
O(t2) = {p3}.
p2
1
t2
1
p3
22. Основные определения
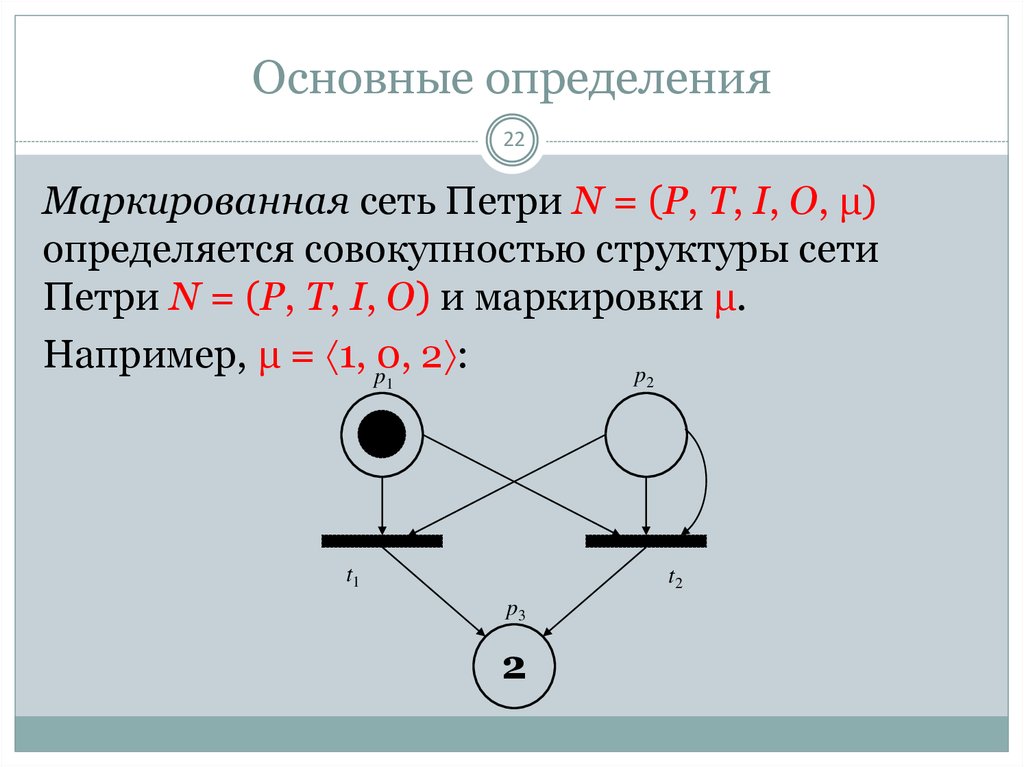
22Маркированная сеть Петри N = (P, T, I, O, μ)
определяется совокупностью структуры сети
Петри N = (P, T, I, O) и маркировки μ.
Например, μ = 1, p0, 2 :
p
2
1
t1
t2
p3
2
23. Основные определения
23Матричный вид сети Петри N = (P, T, I, O)
задается парой (D–, D+), где:
D–[k, i] = ^#(pi, tk) – кратность дуги, ведущей из
позиции pi в переход tk;
D+[k, i] = #^(tk, pi) – кратность дуги, ведущей из
перехода tk в позицию pi,
для произвольных 1 ≤ k ≤ m, 1 ≤ i ≤ n. При этом
μ′ = μ – e[k]D– + e[k]D+ = μ + e[k]D.
24. Запуск сетей Петри
24Сеть Петри выполняется посредством запусков
переходов. При этом образуется новая
маркировка μ′:
μ′(p) = μ(p) – ^#(p, t) + #^(t, p),
где:
^#: P T → Nat;
#^: T P → Nat;
μ(p) ≥ ^#(p, t);
p P.
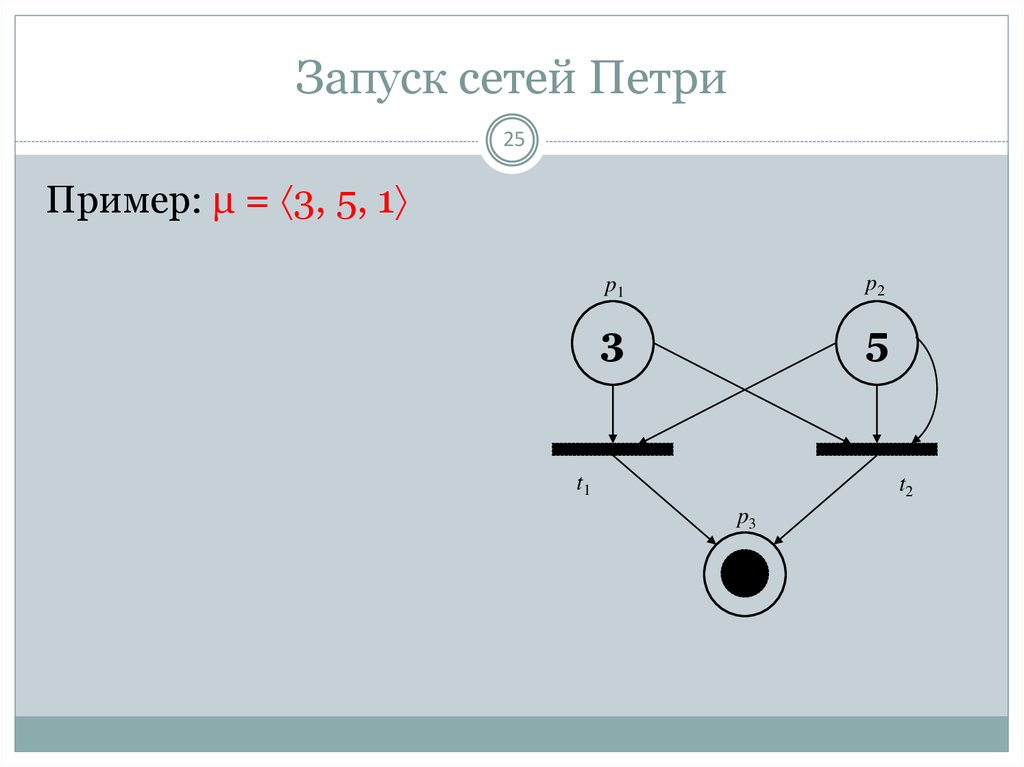
25. Запуск сетей Петри
25Пример: μ = 3, 5, 1
p1
p2
3
5
t1
t2
p3
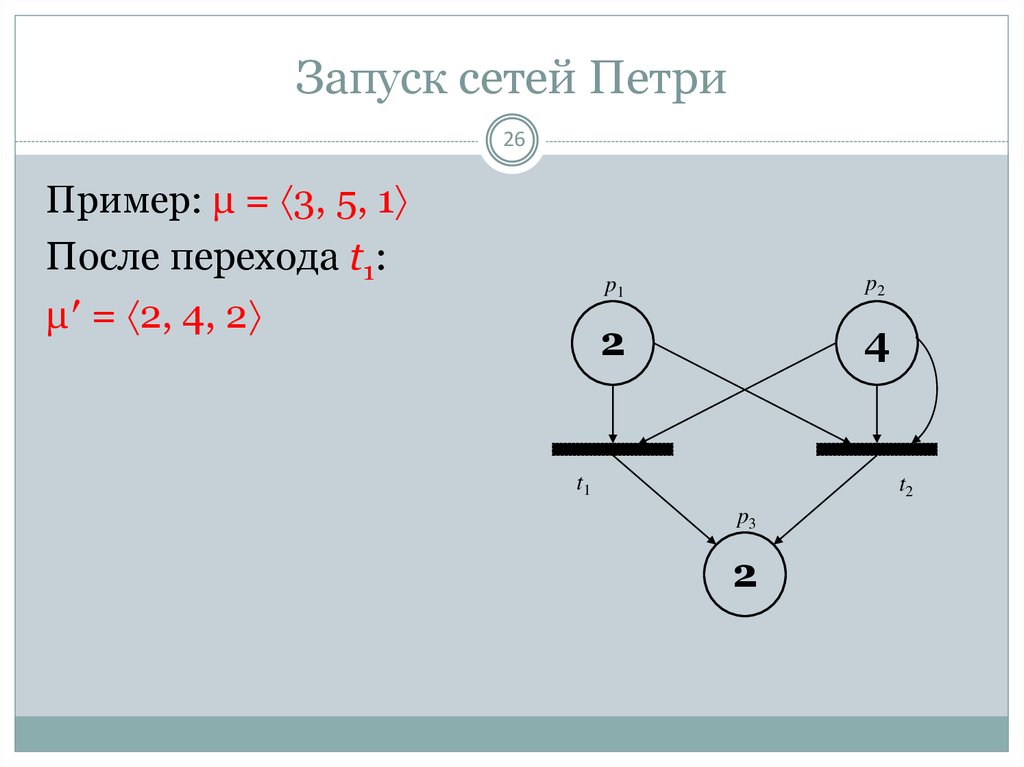
26. Запуск сетей Петри
26Пример: μ = 3, 5, 1
После перехода t1:
μ′ = 2, 4, 2
p1
p2
2
4
t1
t2
p3
2
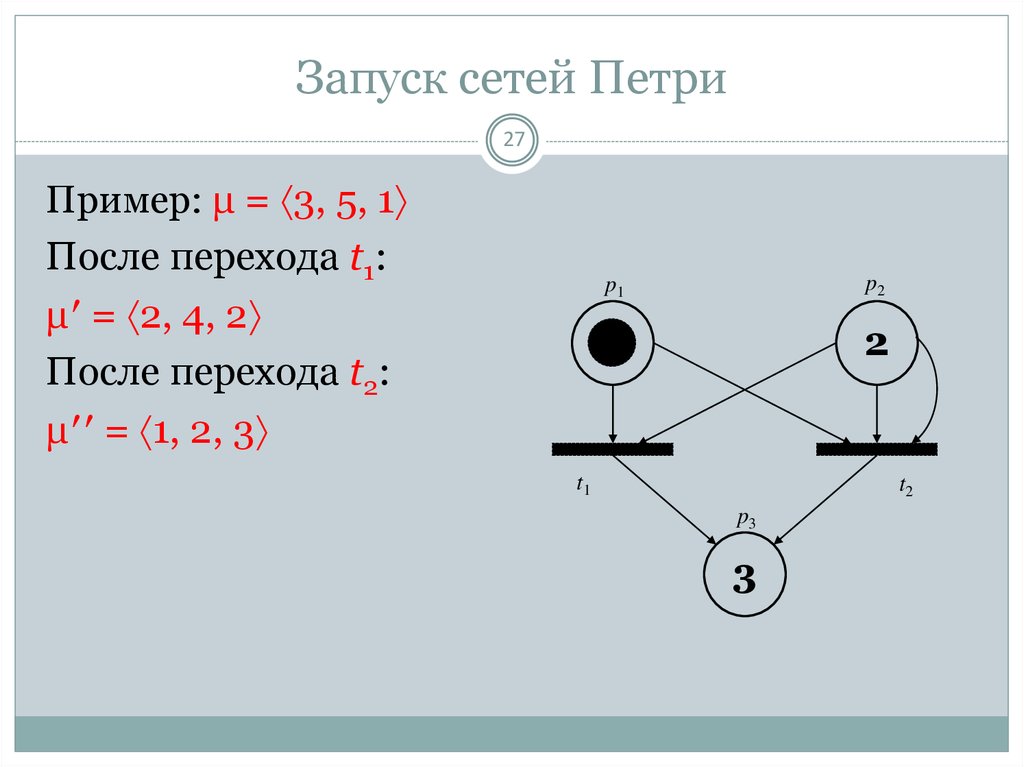
27. Запуск сетей Петри
27Пример: μ = 3, 5, 1
После перехода t1:
μ′ = 2, 4, 2
После перехода t2:
μ′′ = 1, 2, 3
p2
p1
2
t1
t2
p3
3
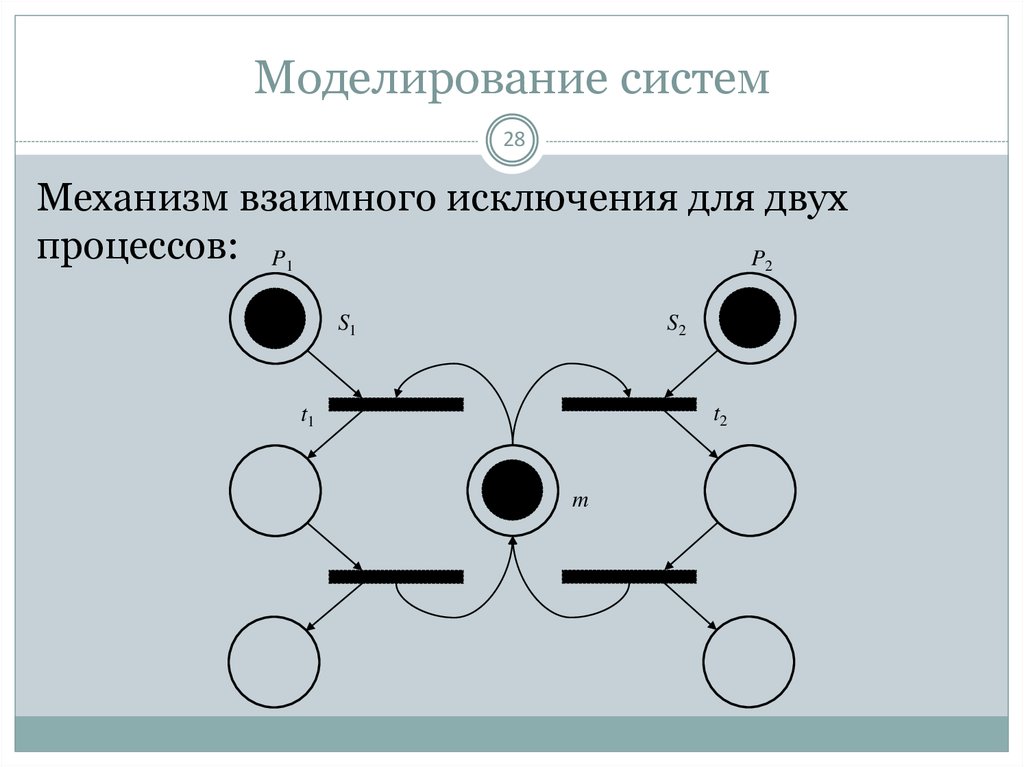
28. Моделирование систем
28Механизм взаимного исключения для двух
процессов: P
P
2
1
S2
S1
t2
t1
m
29. Моделирование систем
29Простой семафор S:
n – текущее значение счётчика;
Nmax – максимальное значение счётчика;
Р – операция блокирования семафора (WaitOne,
WaitForSingleObject, acquire, …);
V – операция деблокирования семафора
(Release, ReleaseSemaphore, release, …).
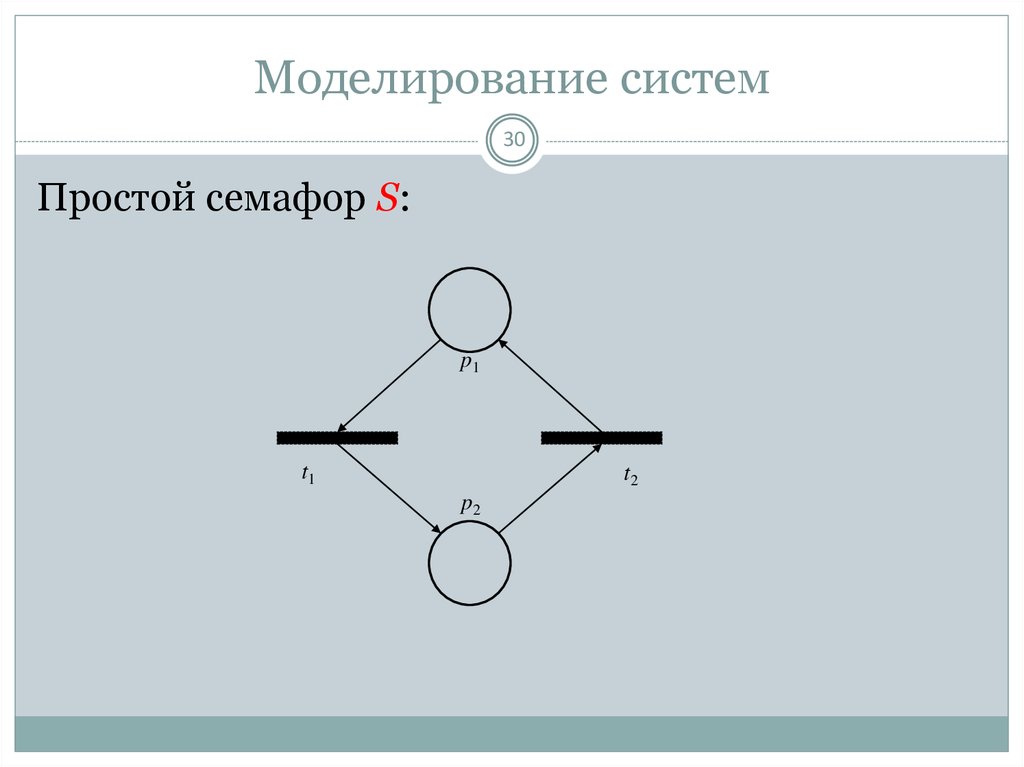
30. Моделирование систем
30Простой семафор S:
p1
t1
t2
p2
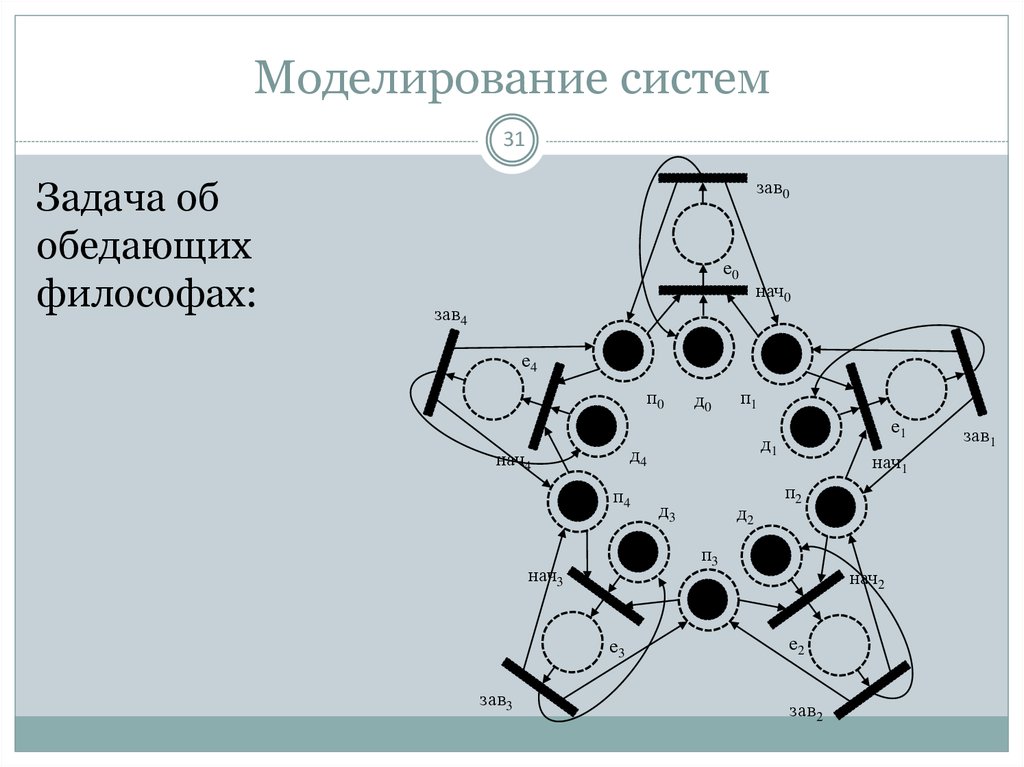
31. Моделирование систем
31Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
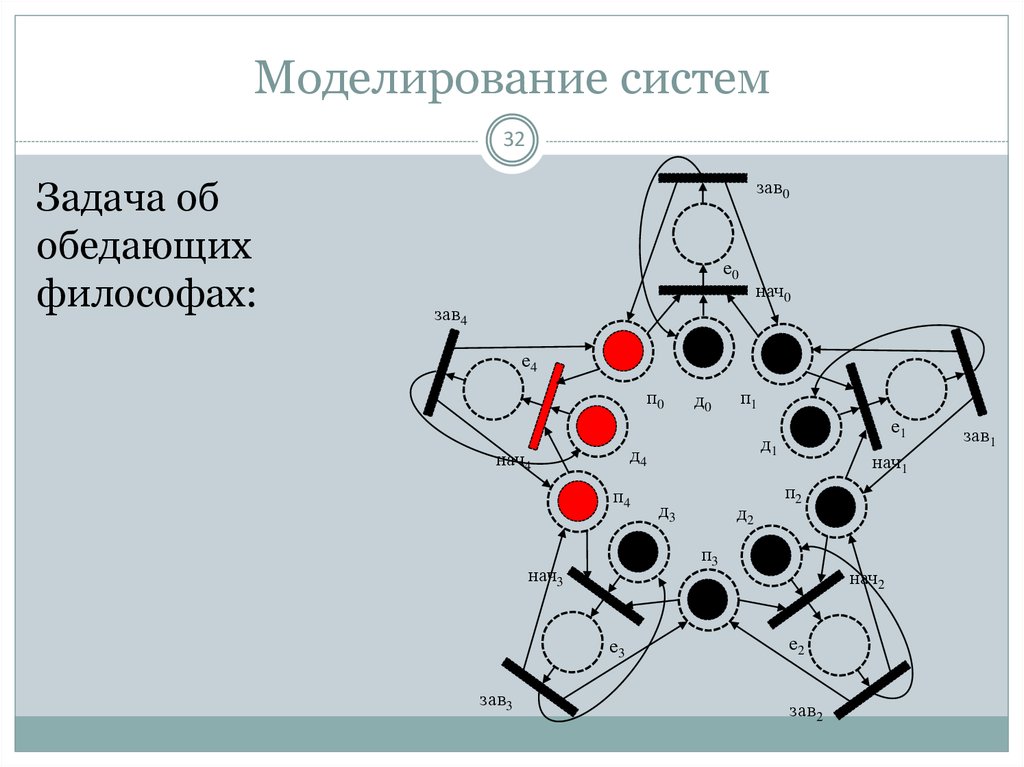
32. Моделирование систем
32Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
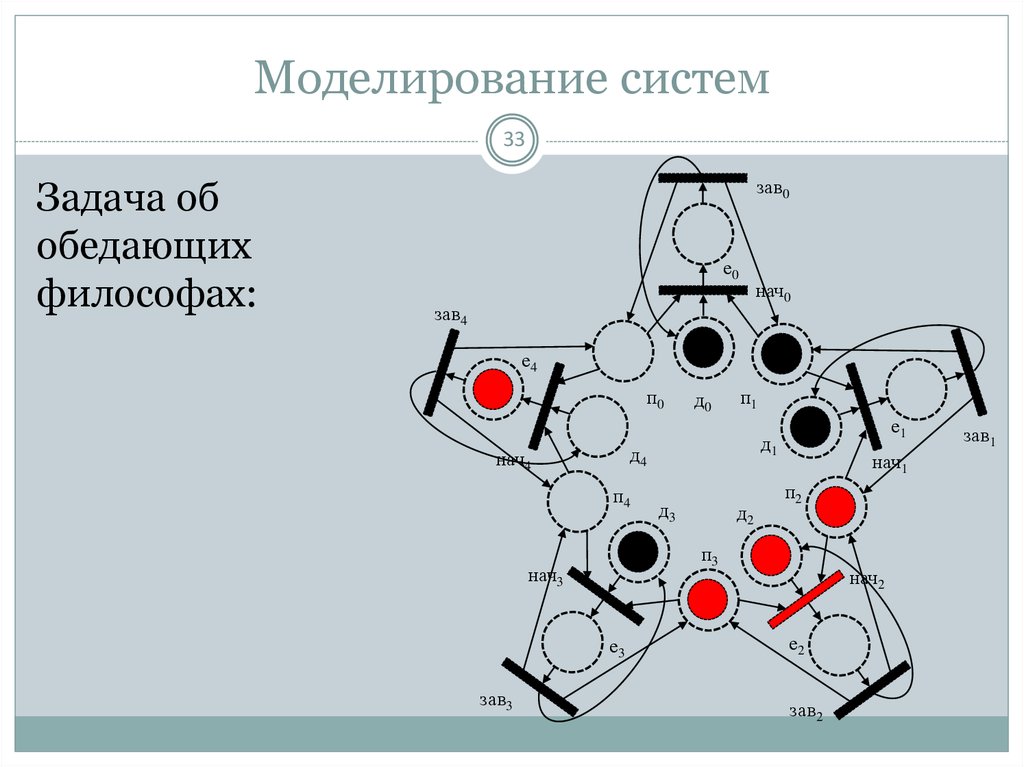
33. Моделирование систем
33Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
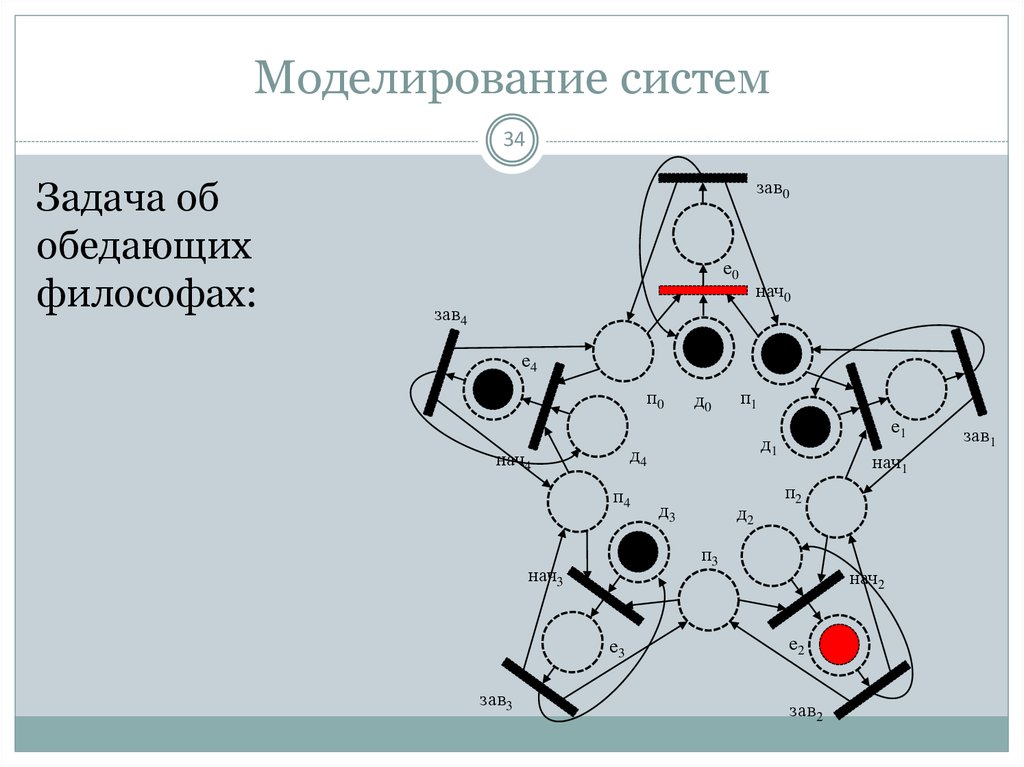
34. Моделирование систем
34Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
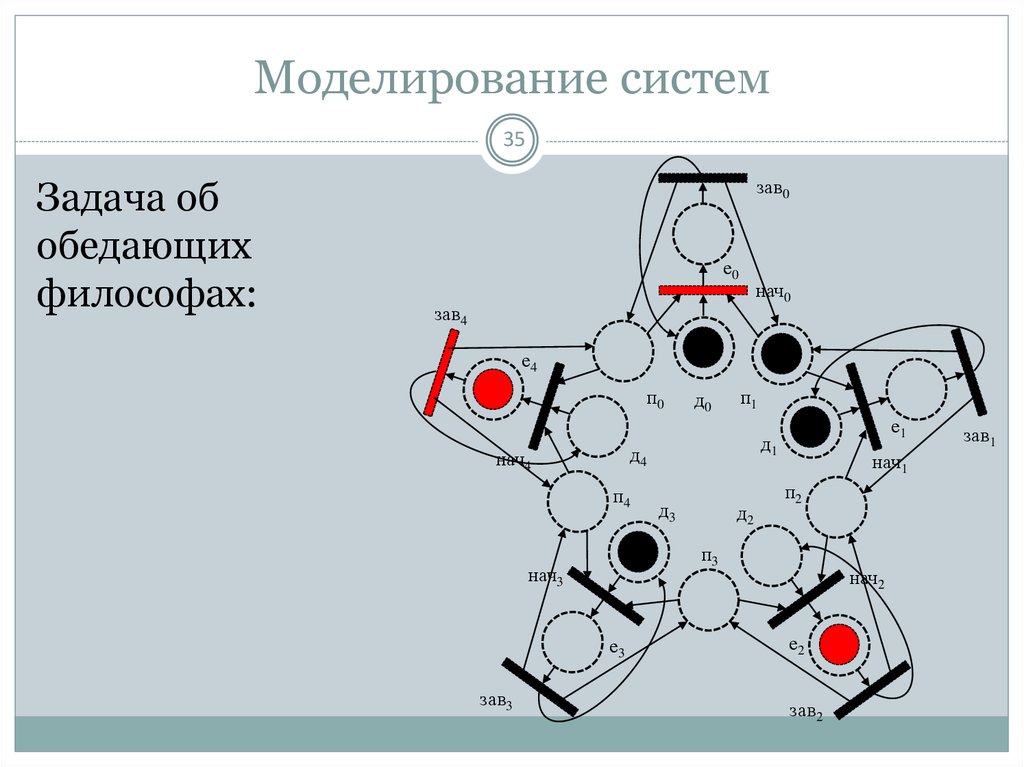
35. Моделирование систем
35Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
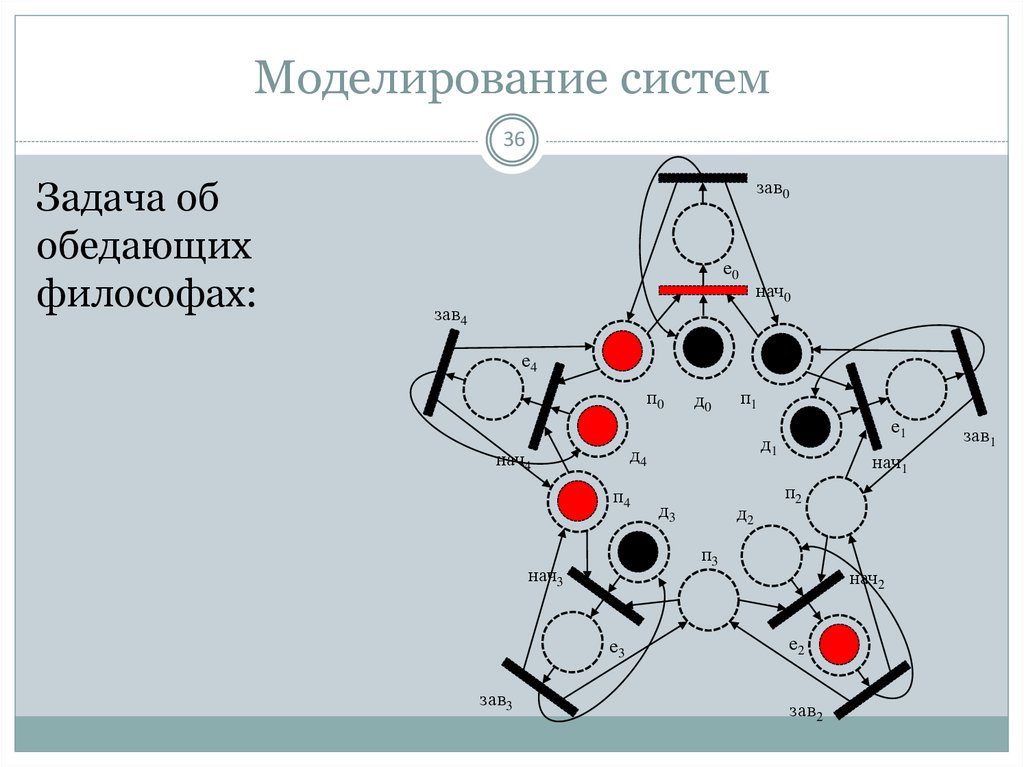
36. Моделирование систем
36Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
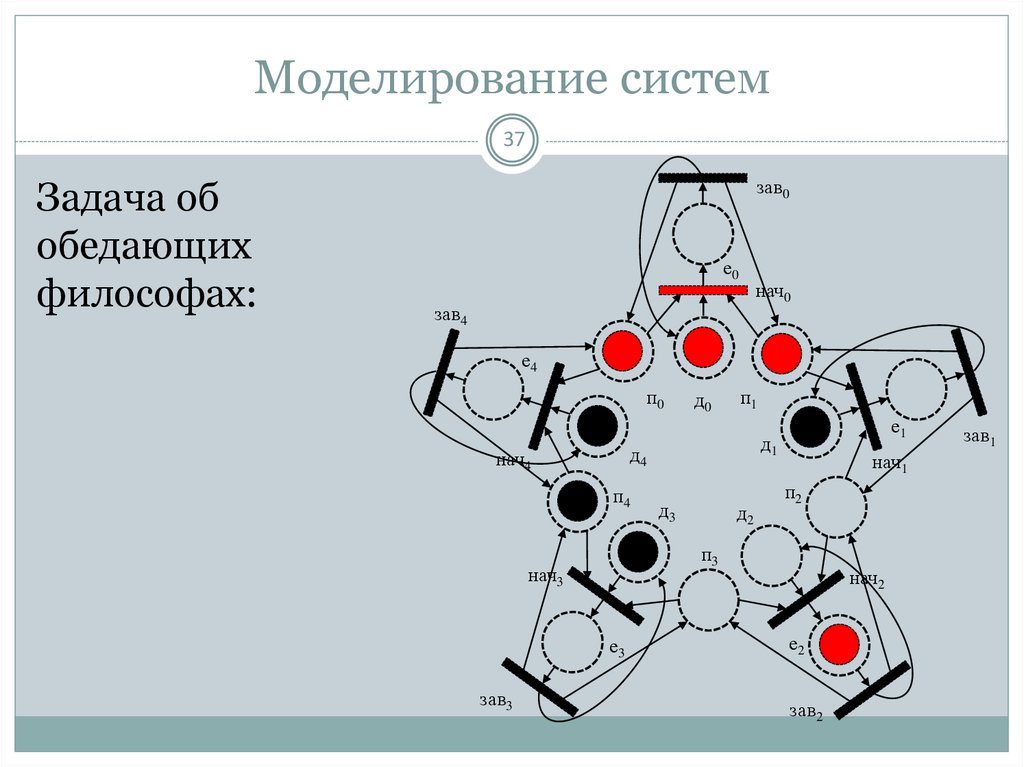
37. Моделирование систем
37Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1
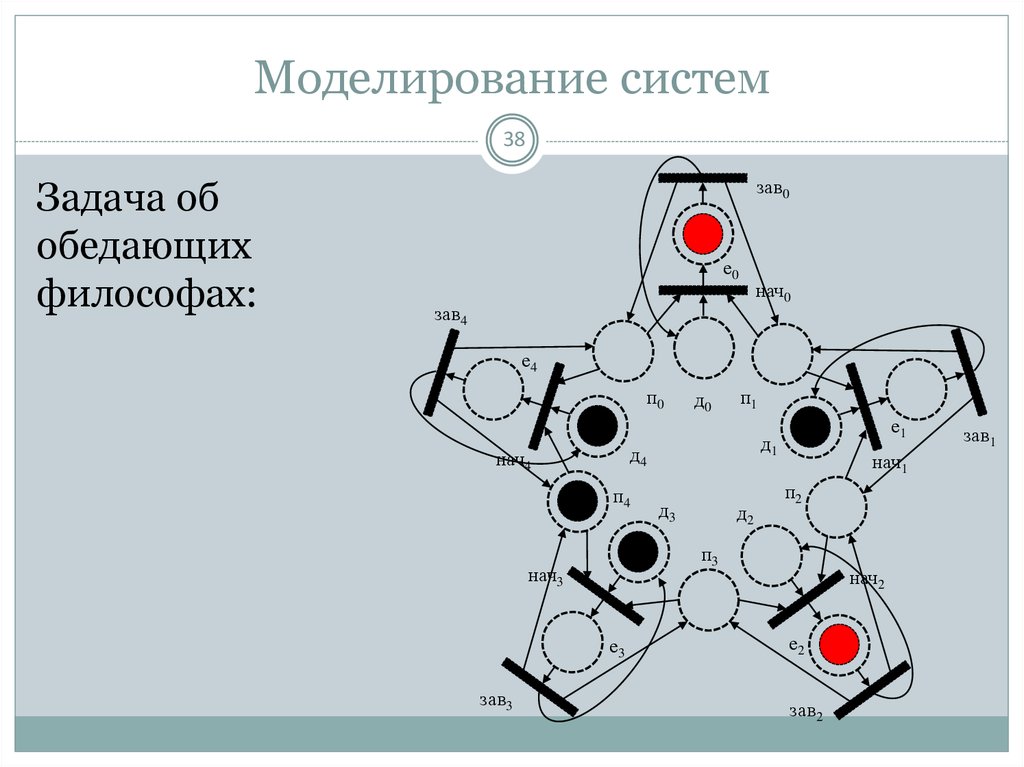
38. Моделирование систем
38Задача об
обедающих
философах:
зав0
е0
нач0
зав4
е4
п0
п1
п4
е1
д1
д4
нач4
д3
д2
нач1
п2
п3
нач3
е3
зав3
д0
нач2
е2
зав2
зав1























 mathematics
mathematics








