Similar presentations:
Функция арифметического квадратного корня у х
1. Китайская пословица гласит: « Я слушаю,-я забываю; Я вижу,-я запоминаю; Я делаю,- я усваиваю»
2.
Функция арифметическогоквадратного корня
у х
3. «Из истории математики» Впервые слово «функция» употребил Готфрид Вильгельм Лейбниц еще в XVII веке (слово «функция» происходит
от латинского functio — исполнение,осуществление)
В 1637 году Декарт дает первое
определение функции
В 1755 году
Леонард Эйлер
дает общее
определение
функции
В 1671 году Ньютон
под функцией стал
понимать
переменную
величину, которая
изменяется с
течением времени.
4. Функция – это зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное
Определение функцииФункция – это зависимость переменной у
от переменной х, при которой каждому
значению переменной х соответствует
единственное значение переменной у.
х–независимая переменная или аргумент
у–зависимая переменная или значение
функции
5. Что называют графиком функции? Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а
ординаты –соответствующим значениям функции
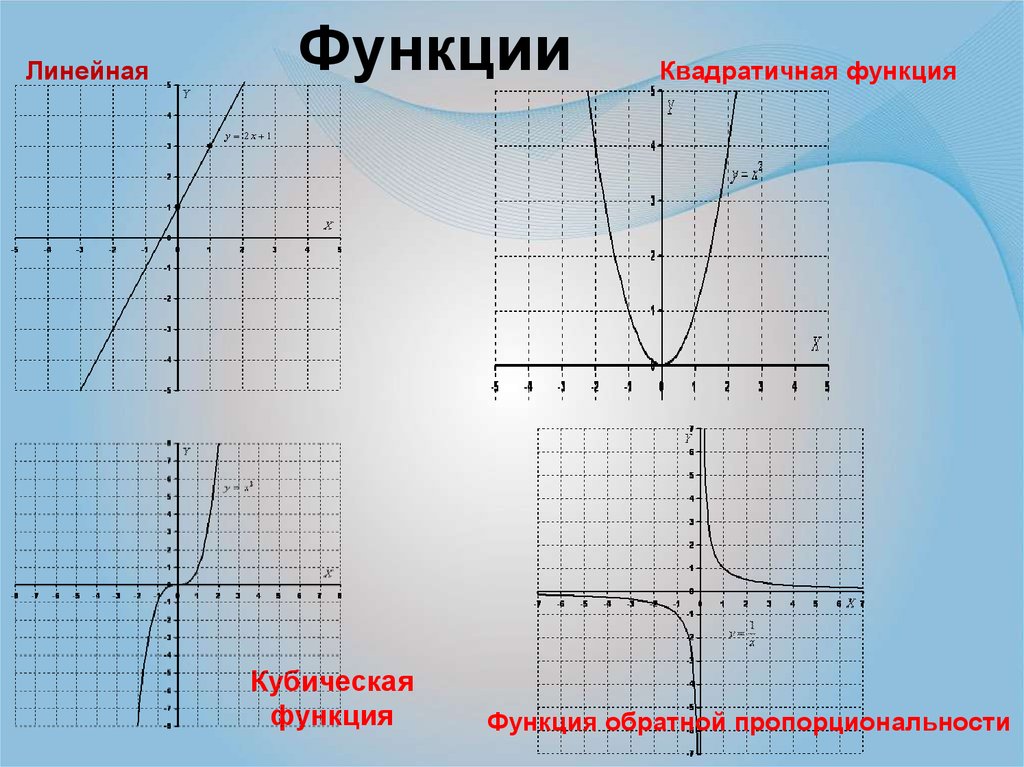
6. Функции
ЛинейнаяФункции
Кубическая
функция
Квадратичная функция
Функция обратной пропорциональности
7.
Функция арифметического квадратногокорня
у х,
её свойства и график
у х
8. 1.Научимся строить графики функций
у к ху х n m
у к х
2.Решать графически уравнения
3.Находить наименьшее и
наибольшее значения функции
4.Определять принадлежность
точки графику
5.Определять принадлежность
переменной промежутку
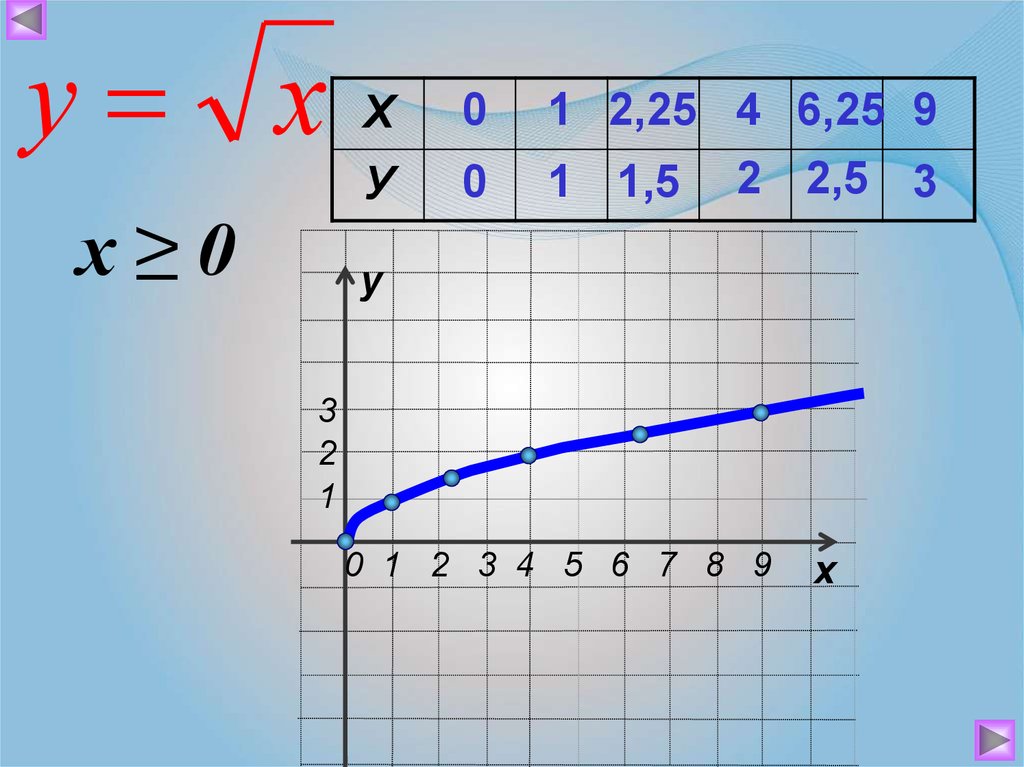
9.
у хх≥0
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х
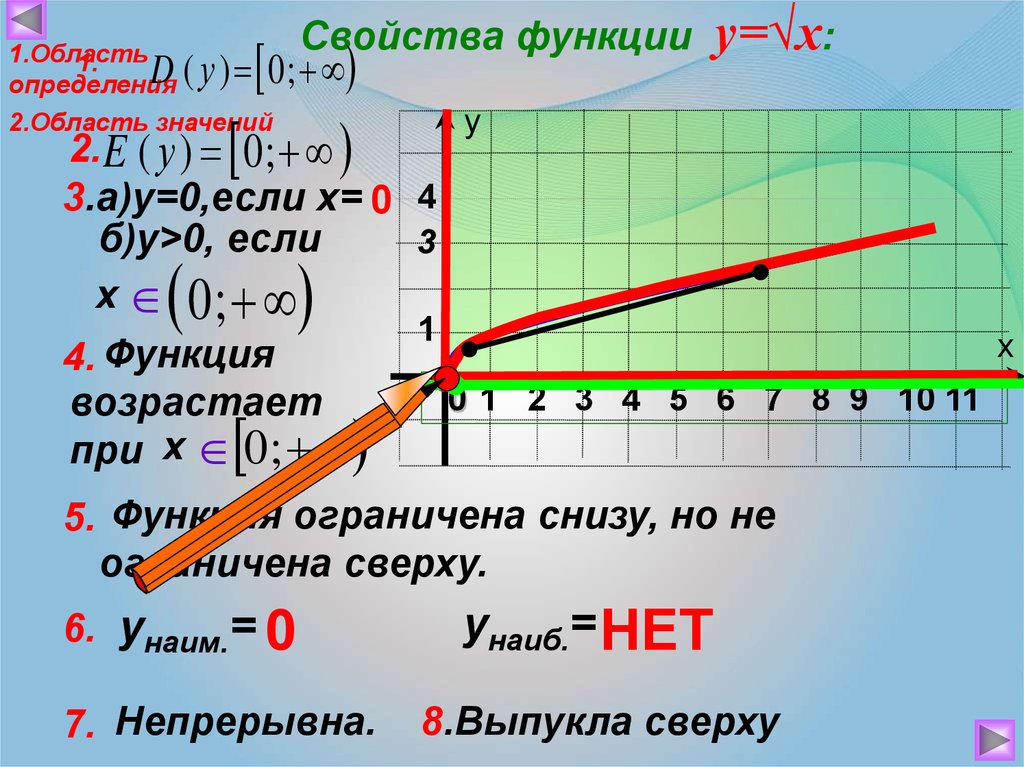
10.
Свойства функцииD ( у ) 0 ;
1.Область
1.
определения
2.Область значений
у=√х:
у
2. E ( у ) 0 ;
3.а)у=0,если х= 0 4
б)у>0, если
3
х 0;
1
х
4. Функция
-1 0 1 2 3 4 5 6 7 8 9 10 11
возрастает
при х 0 ;
5. Функция ограничена снизу, но не
ограничена сверху.
6. унаим.= 0
7. Непрерывна.
унаиб.= НЕТ
8.Выпукла сверху
11.
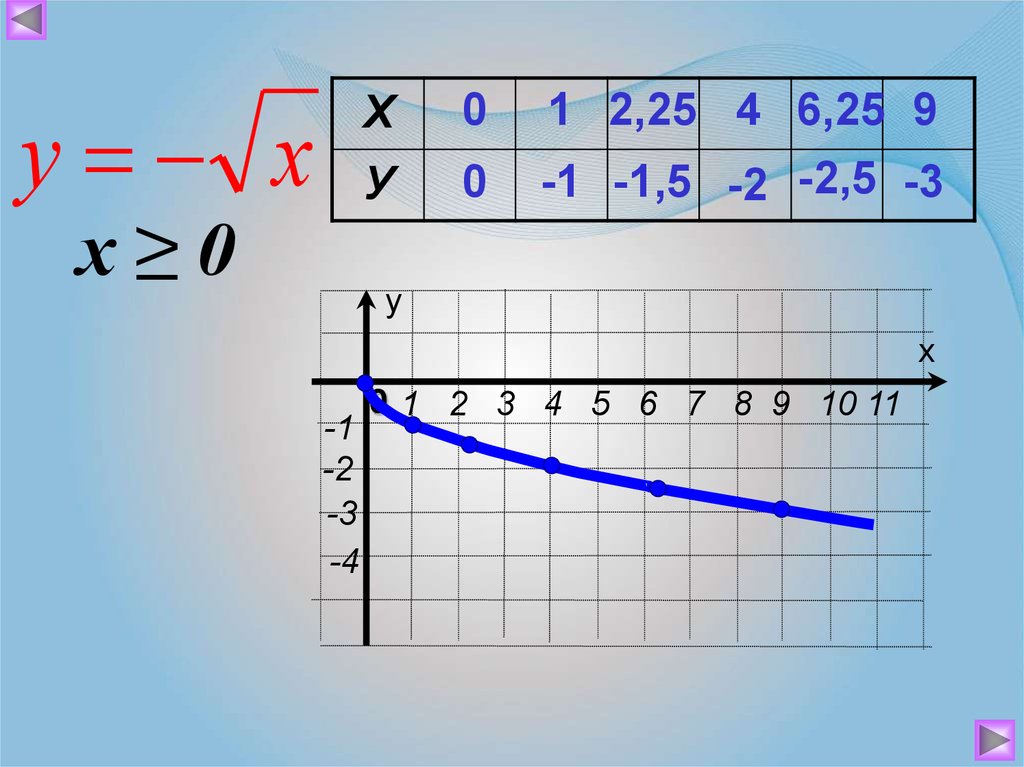
у хх≥0
Х
0
У
0
1 2,25 4 6,25 9
-1 -1,5 -2 -2,5 -3
у
х
-1
-2
-3
-4
0 1 2 3 4 5 6 7 8 9 10 11
12.
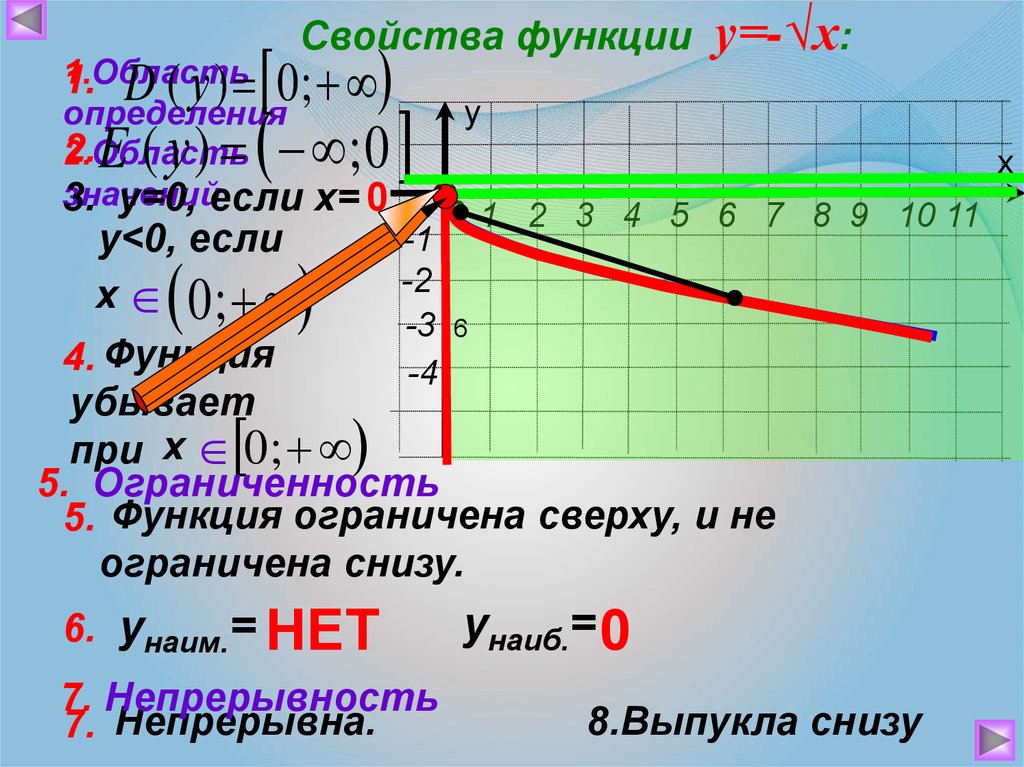
Свойства функции1.Область
1. D ( у ) 0 ;
определения
2.
2.Область
значений
3. у=0, если х= 0
E ( у ) ; 0
у=-√х:
у
х
0 1 2 3 4 5 6 7 8 9 10 11
-1
у<0, если
-2
х 0;
-3 6
4. Функция
-4
убывает
при х 0 ;
5. Ограниченность
5. Функция ограничена сверху, и не
ограничена снизу.
6. унаим.= НЕТ
7. Непрерывность
7. Непрерывна.
унаиб.= 0
8.Выпукла снизу
13. Задание1. Построить график таблица №1а)
Задание1. Построитьграфик у
х
таблица №1а)
Построить графики
функций (таблица1б)
1. у =2*√х (1вариант)
2. у=0,5*√х
1. у= -2*√х (2вариант)
2. у= -0,5*√х
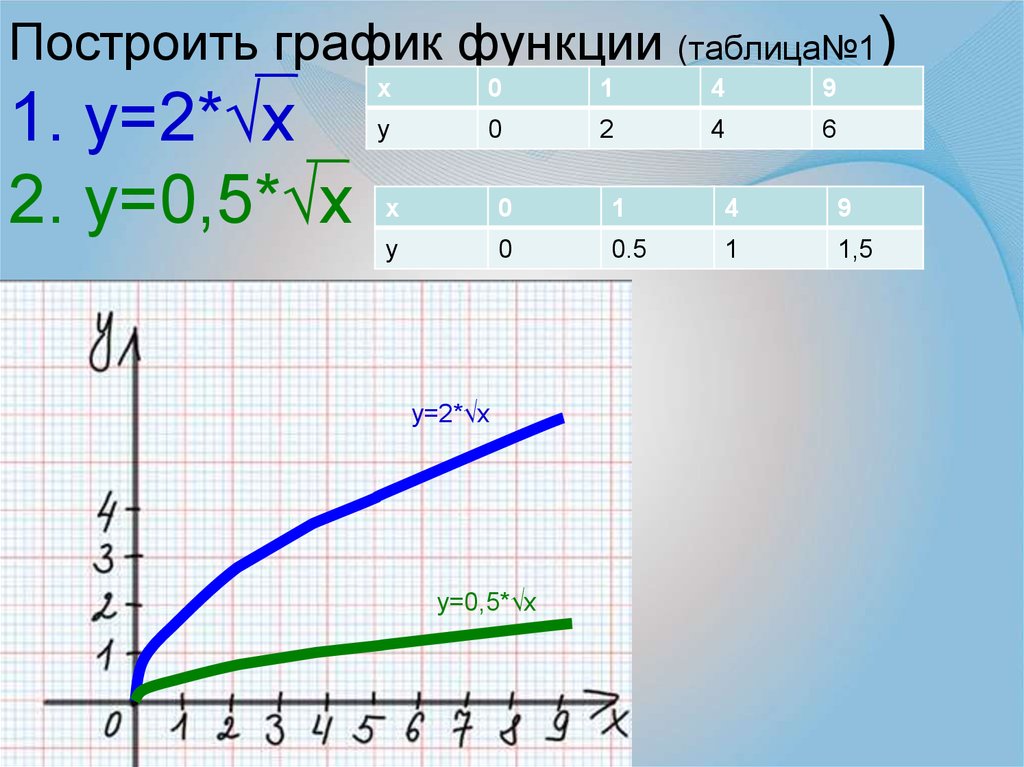
14. Построить график функции (таблица№1) 1. у=2*√х 2. у=0,5*√х
х0
1
4
9
у
0
2
4
6
х
0
1
4
9
у
0
0.5
1
1,5
у=2*√х
у=0,5*√х
15.
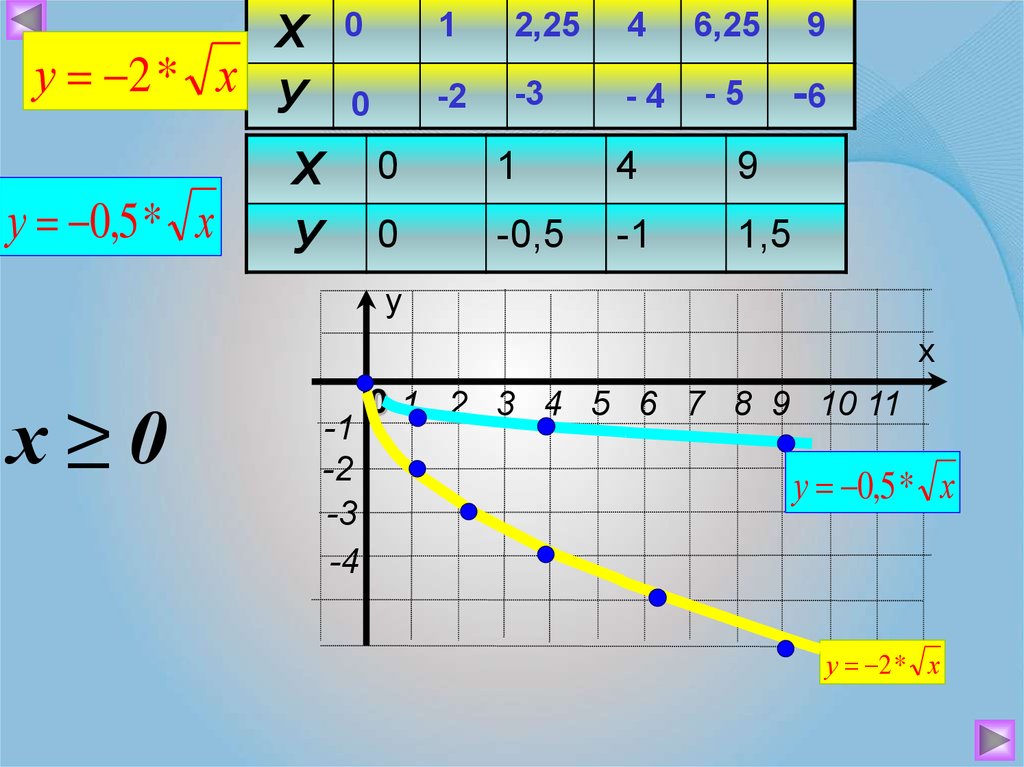
Ху 2 * х У
у 0,5 * х
0
1
2,25
4
6,25
9
0
-2
-3
-4
-5
-6
Х
У
0
1
4
9
0
-0,5
-1
1,5
у
х
х≥0
-1
-2
-3
-4
0 1 2 3 4 5 6 7 8 9 10 11
у 0,5 * х
у 2 * х
16. Графическое решение уравнений
17.
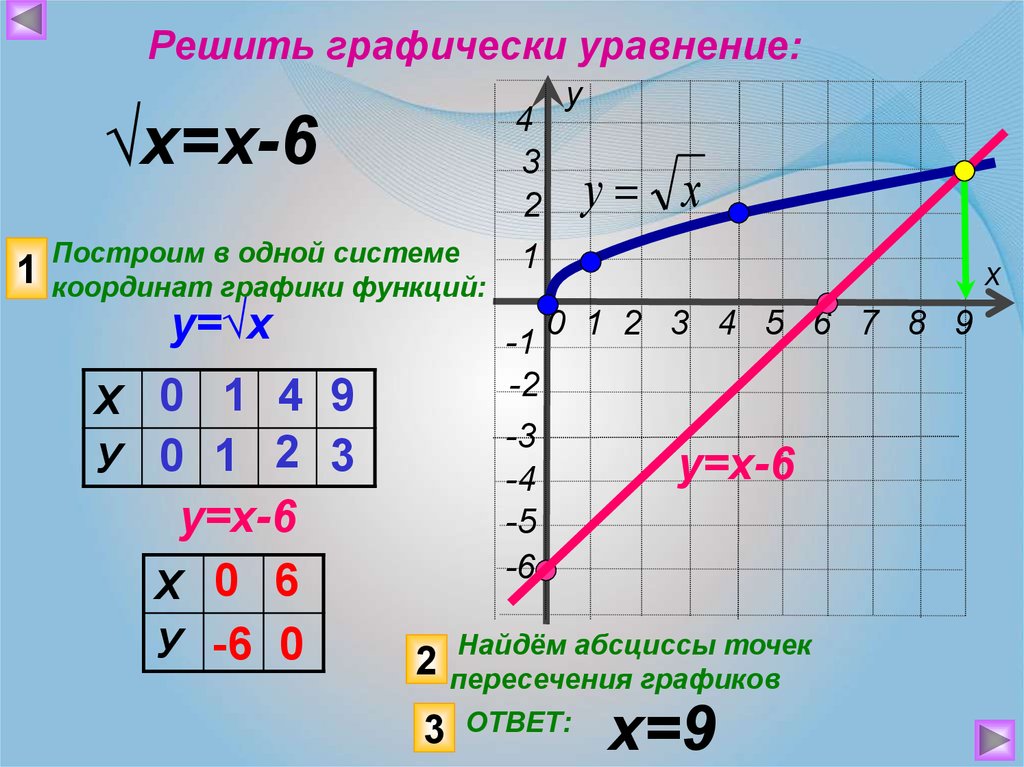
Решить графически уравнение:√х=х-6
1
4
3
2
Построим в одной системе
координат графики функций:
у=√х
у=х-6
Х 0 6
У -6 0
2
3
у х
1
-1
-2
-3
-4
-5
-6
Х 0 1 4 9
У 0 1 2 3
у
х
0 1 2 3 4 5 6 7 8 9
у=х-6
Найдём абсциссы точек
пересечения графиков
ОТВЕТ:
х=9
18. Задание 2 таблица №2
№13.9 а)Решите графически
уравнение
х х
19.
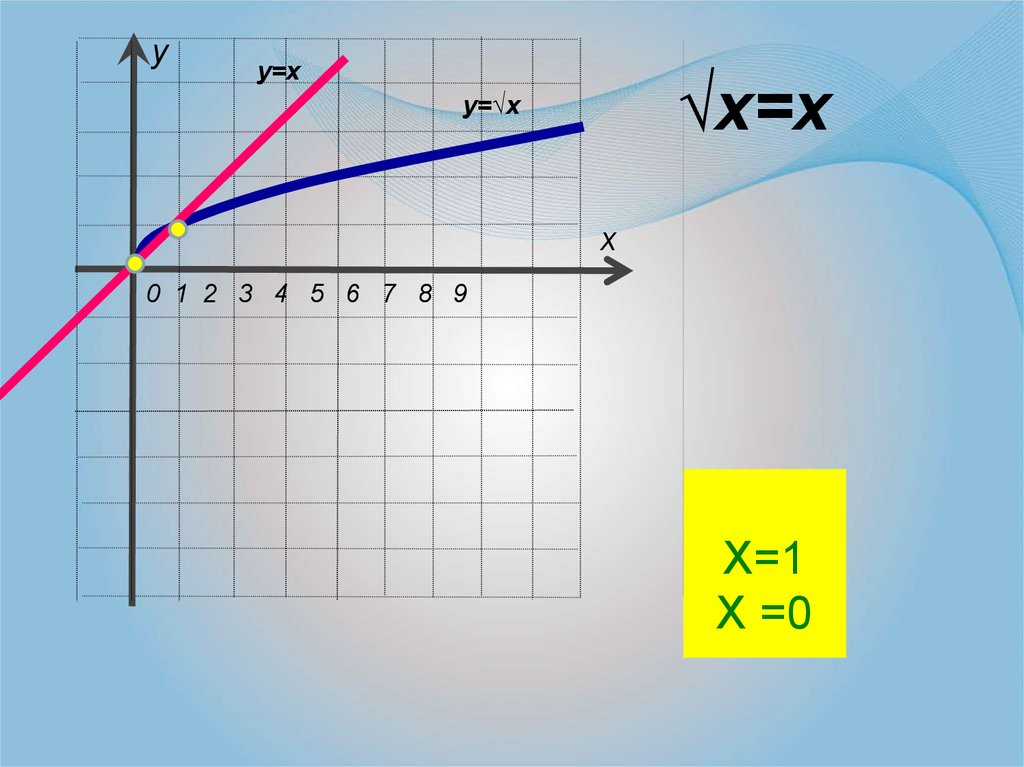
уу=х
√х=х
у=√х
х
0 1 2 3 4 5 6 7 8 9
Х=1
Х =0
20.
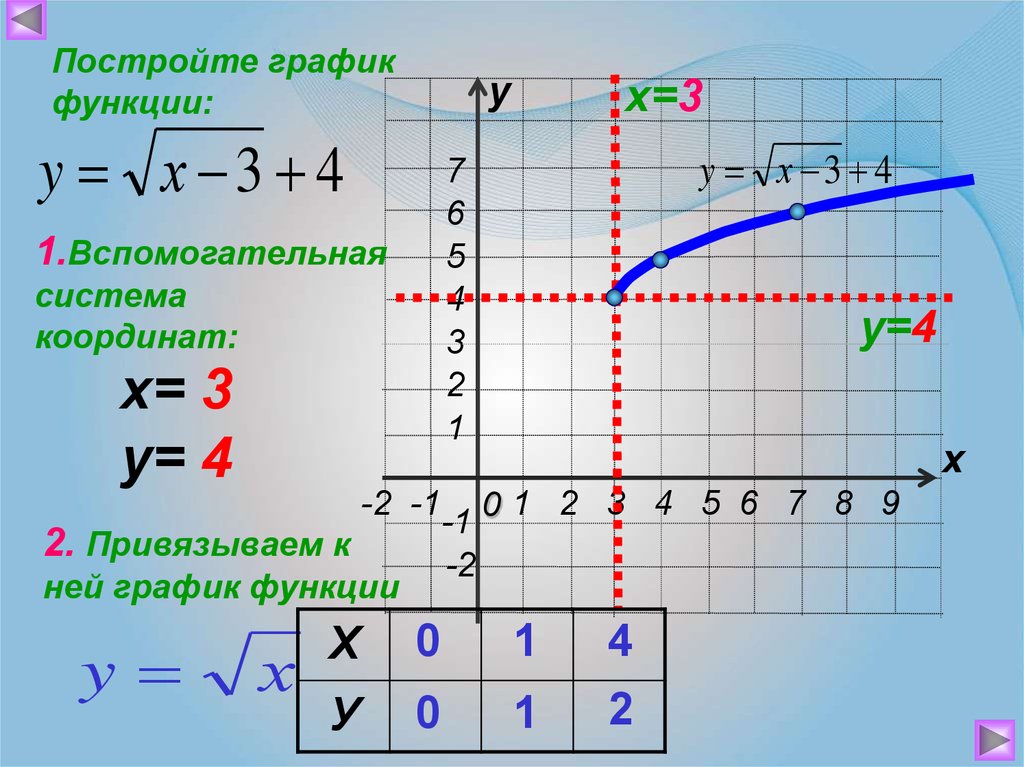
Постройте графикфункции:
у
y х 3 4
система
координат:
х= 3
у= 4
-2 -1
2. Привязываем к
ней график функции
х
y х 3 4
7
6
5
4
3
2
1
1.Вспомогательная
y
х=3
-1
-2
у=4
х
01 2 3 4 5 6 7 8 9
Х
0
1
У
0
1
4
2
21. Задание 3 таблицы №3 и №4
Построить графики функцийу х 2 2
у х 1 1
22. График функции смещён вправо и вверх на две единицы
График функции у х 2 2смещён вправо и вверх на две
единицы
График функции у х 1 1
смещён влево и вниз на
единицу
23. Работаем в электронной таблице Excel Строим графики функций
у ху 1,2 * х ,
у х 2 3
у х
у х 2
у 2 х 2
24. (№13.4 а),б) 1.Определяем принадлежность точки графику, не выполняя построения у = √х а)А(2; √2) б)В(1;0) Ответ: а) б) В
(№13.4 а),б)1.Определяем принадлежность точки
графику, не выполняя построения
у = √х
а)А(2; √2) б)В(1;0) Ответ: а) А ∈ графику функции
б) В
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х
25. Определение промежутков принадлежности переменной и нахождение наибольшего и наименьшего значения функции
26.
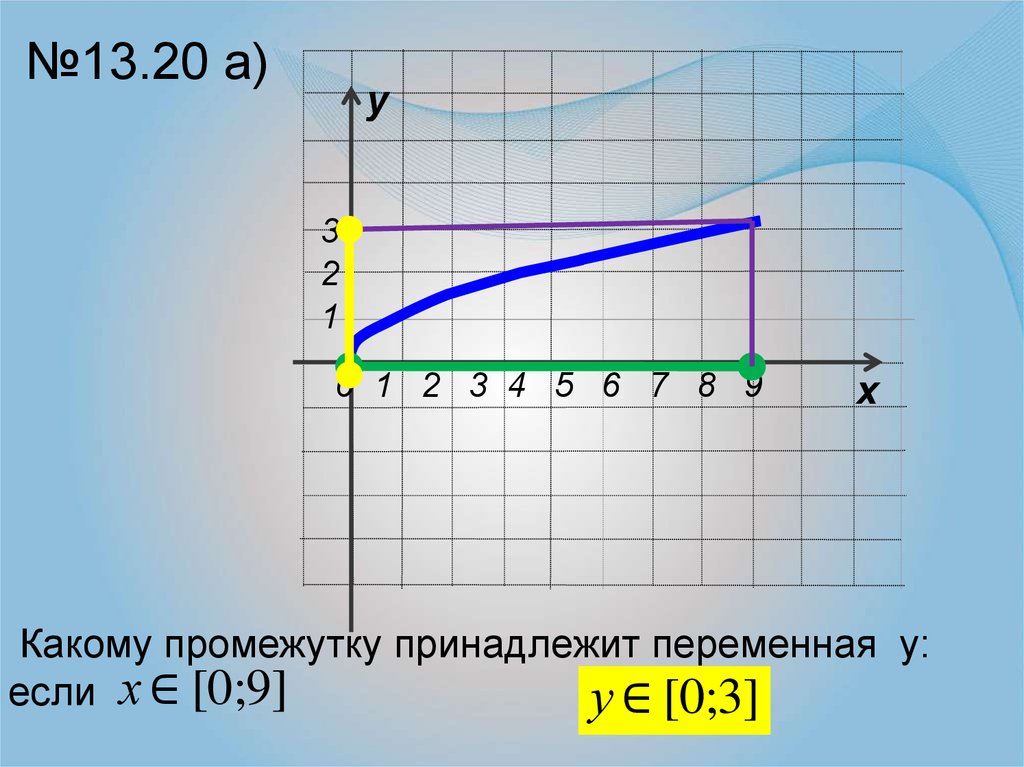
№13.20 а)у
3
2
1
0 1 2 3 4 5 6 7 8 9
х
Какому промежутку принадлежит переменная у:
если х ∈ [0;9]
у ∈ [0;3]
27.
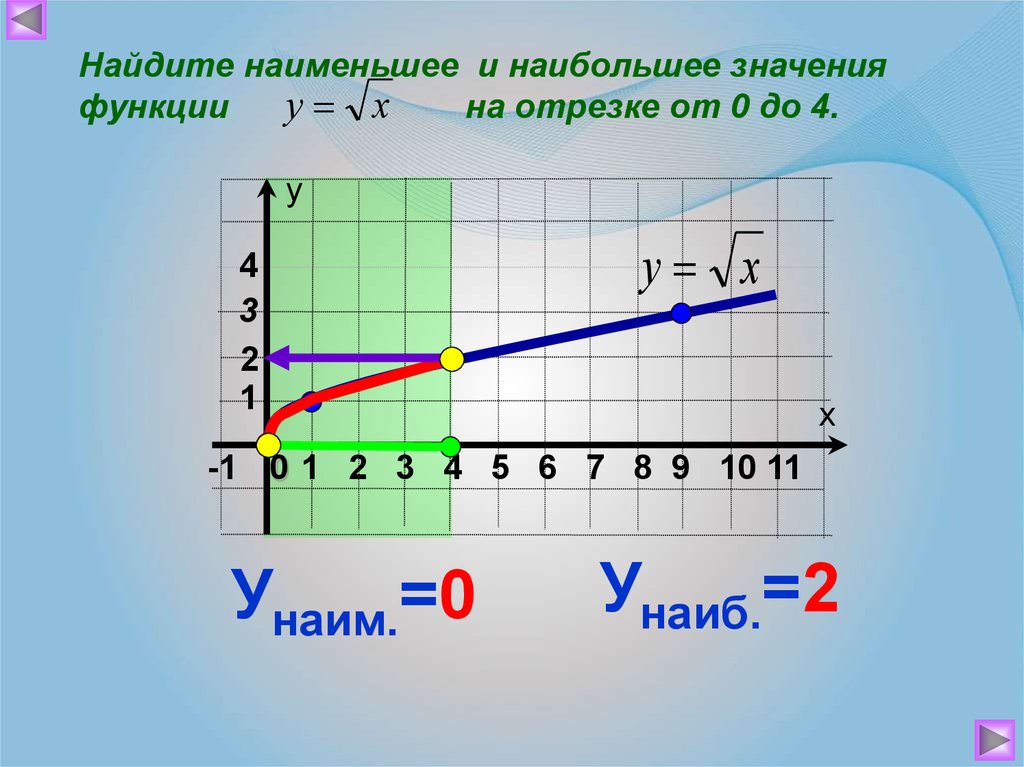
Найдите наименьшее и наибольшее значенияу х
функции
на отрезке от 0 до 4.
у
4
3
2
1
у х
х
-1 0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=0
Унаиб.=2
28.
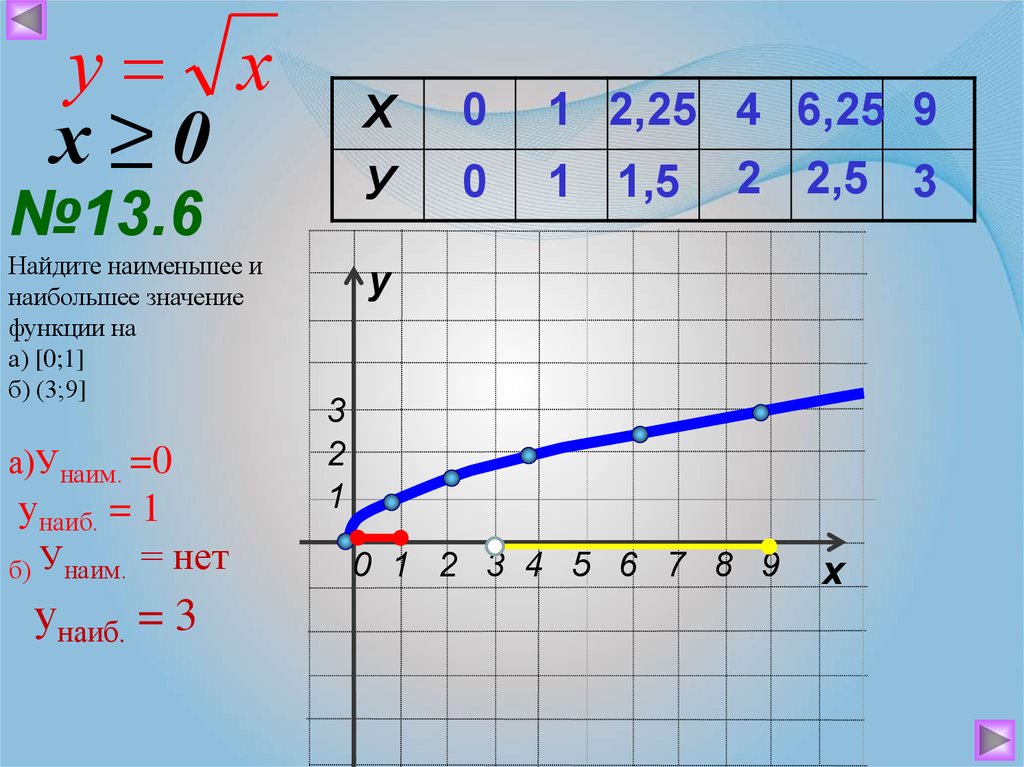
у хх≥0
№13.6
Найдите наименьшее и
наибольшее значение
функции на
а) [0;1]
б) (3;9]
а)Унаим. =0
унаиб. = 1
б) Унаим. = нет
унаиб. = 3
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х
29.
ЗУ
Н
30. 1.Научились строить графики функций
у ху х n m
у х
у к х
2.Решать графически уравнения
3.Находить наименьшее и
наибольшее значения функции
4.Определять принадлежность
точки графику
5.Определять принадлежность
переменной промежутку
31.
Функция арифметического квадратного корняСвойства функции у х,
1.Область определения функции – все значения независимой
переменной х. Обозначение: D( f )=[0;+∞)
2.Область значений функции – все значения зависимой
переменной у.
у
Обозначение: Е( f )= [0;+∞)
3.Функция возрастает при х [0;+∞)
4.Непрерывна
5.Ограничена снизу
6.Выпукла сверху
Графиком функции является ветвь параболы.
32.
Домашнее задание§13
Выполнить №13.11, 13.16, 13.24 ,13.31,
у
у х
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 х
33.
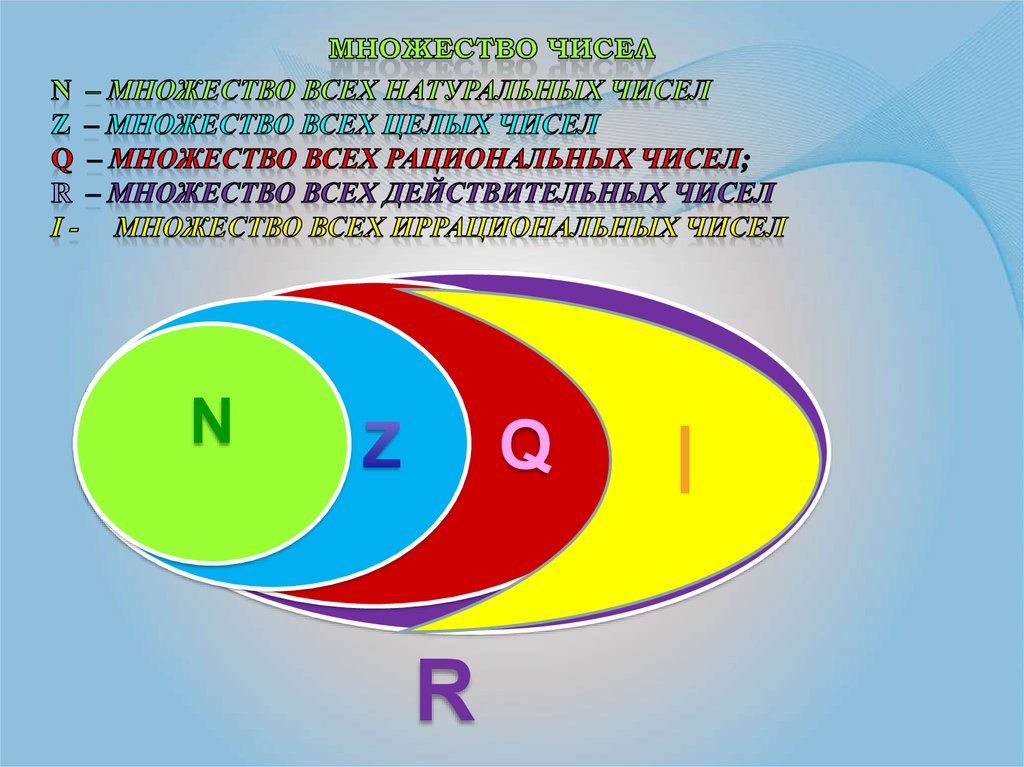
34. 1,(12)= √0,04=0,2 √2,25=1,5
QR
I
1,(12)=
√0,04=0,2
√2,25=1,5
N
R
35.
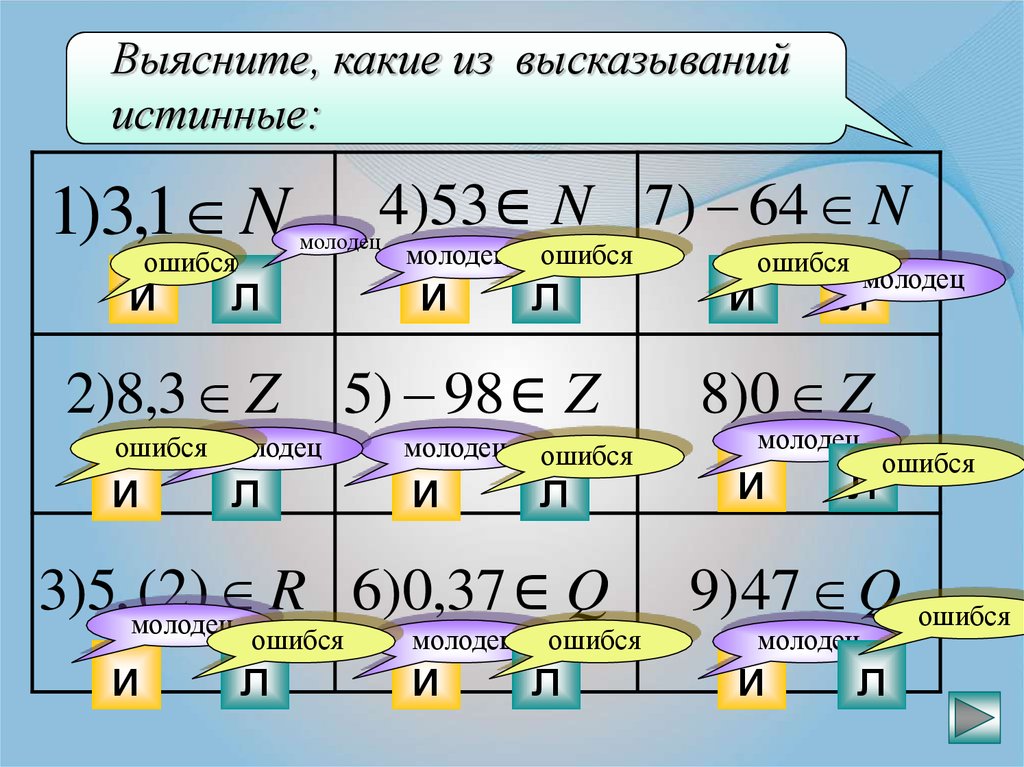
Выясните, какие из высказыванийистинные:
1)3,1 N
ошибся
и
4)53 ∈ N 7) 64 N
молодец
л
2)8,3 Z
и
ошибся
л
5) 98 ∈ Z
ошибся молодец
и
молодец
л
молодец
и
ошибся
л
3)5,молодец
(2) R 6)0,37 ∈ Q
и
ошибся
л
молодец
и
ошибся
л
и
ошибся
молодец
л
8)0 Z
молодец
и
л
ошибся
9)47 Q ошибся
молодец
и
л
36. Устно
1. 13 12 5Устно
2. 36 * 0,01 0,6
3. 121 * 0,1 0,06 4,4
4.(3√7)² = 63
5.3(√7)²= 21
6.Сравните
3√2 и 2√3
3√2 > 2√3
37. Выполните задание 1-6 и вычеркните буквы, соответствующие ответам
мо
д
т
л
р
и
к
ч
г
н
а
о
0,5
3
-2
6
-5
0
8
0,6
0,3
2
0,9
8
3
1. √25 -√49=
2. 3√4 – 6=
3. -3√0,49 +2,6 =
4. (√0,9)2 - 0,3
5. 1/6 *√12) 2 =
6. √4*52 - 62
Отлично
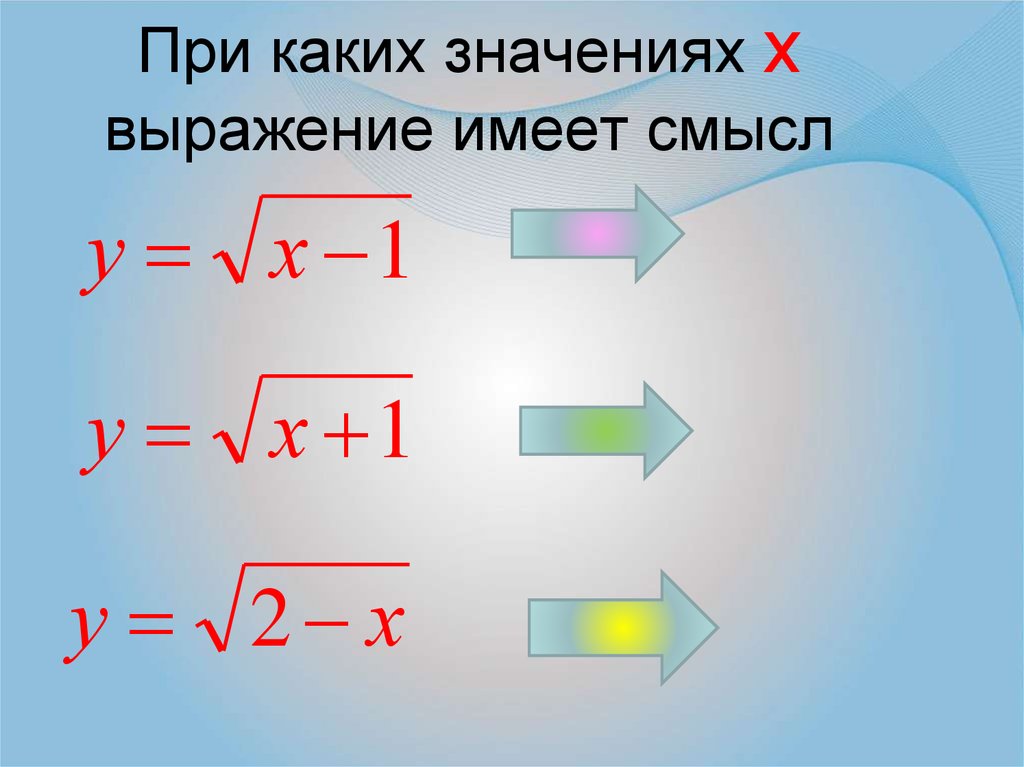
38. При каких значениях х выражение имеет смысл
у х 1х ≥1
у х 1
х ≥-1
у 2 х
х≤2
39. Тест из заданий ГИА
40. Спасибо
41. План урока I. Организационный момент II. Повторение III.Объяснение новой темы а) рассмотрим построение графика функции у =√х ,
у= - √х
б) строим график функции у =√х , у= - √ х в электронной
таблице
Excel.
IV. Актуализация и проверка усвоения изученного
материала:
V. Итог урока. Домашнее задание.
Задания из ГИА(карточки)























 mathematics
mathematics