Similar presentations:
Решение показательных уравнений
1. Решение показательных уравнений.
2.
№ 455а) у= 1 sinх)
2
Решение: D(y)=R
-1 sin х 1
1 -1
=2;
2
1 1 1
=
2
2
max у(х)=2;
(- ; )
min
(- ; )
1
у(х)= 2
б)у=5+3|cos х|
Решение: D(у)=R
-1 cos х 1
0 |cos х| 1
5+3|cos х|=5+30=5+1=6; 5+3|cos х|=5+31=8
max y(х)=8;
min у(х)=6.
3. Изобразить схематически график функции: а)у=-3·2х; б)у=2|х| Если х≥0, то у=2х. Поскольку у=2|х| Строим у=3·2х, а затем ему
Изобразить схематически график функции:а)у=-3·2х;
б)у=2 |х|
Если х≥0, то у=2х. Поскольку у=2|х|
Строим у=3·2х, а затем ему симметричный четная функция, то её график симм.
относиу=-3·2х относительно оси ОХ.
тельно оси ОУ.
4. Изобразить график функции у=(tg 60º)1-х
• Решение.Т. К. tg 60º=√3, то функцию можно
записать в виде у=(√3)1-х
у=√3·(√3)-х
у= √3 ·1/(√3)х. Здесь
а=1/ √3 <1. Значит функция
убывающая.
Если х=0, то у= √3·(1/ √3)0= √3;
Если х=-1, то у=3.
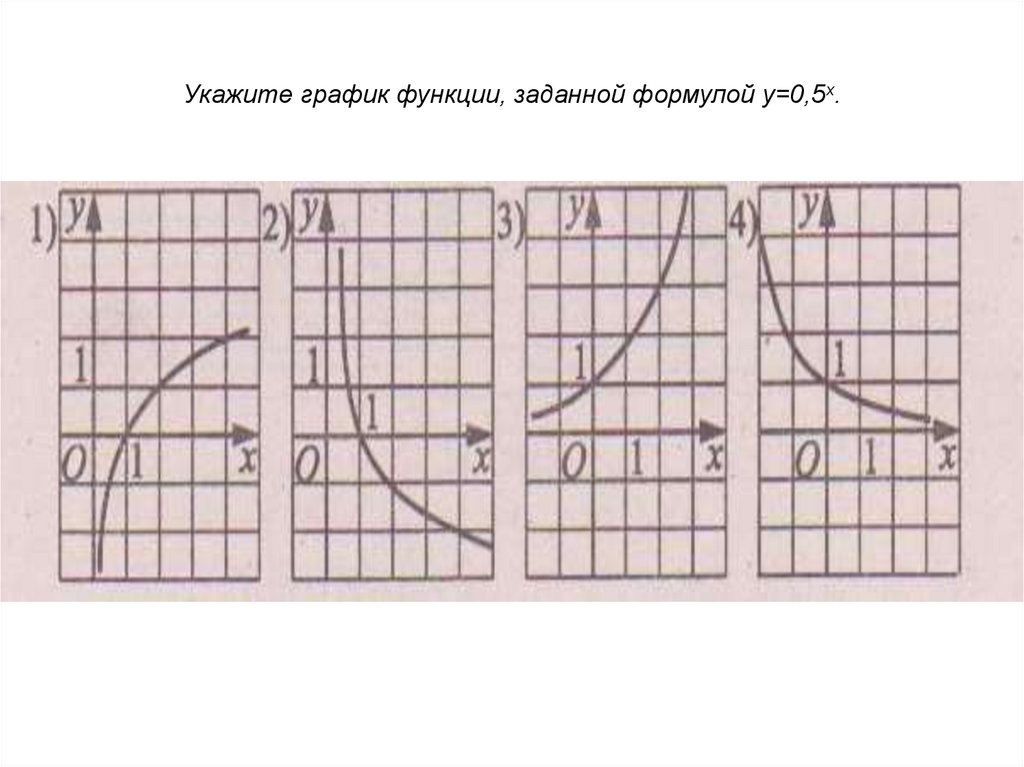
5. Укажите график функции, заданной формулой у=0,5х.
6. Свойства показательной функции у=ах, а>0, а≠1
Свойства показательной функцииу=ах, а>0, а≠1
• 1. D(у)=R
• 2. Е(у)=R+
• 3. При а>1 функция возрастает,
при 0 <а <1 функция убывает.
4. Если ах=ас, то х=с.
7.
• Уравнение, содержащее переменную впоказателе степени, называется
показательным.
• Простейшим примером показательного уравнения служит
уравнение ах=b (где а>0, а≠1).
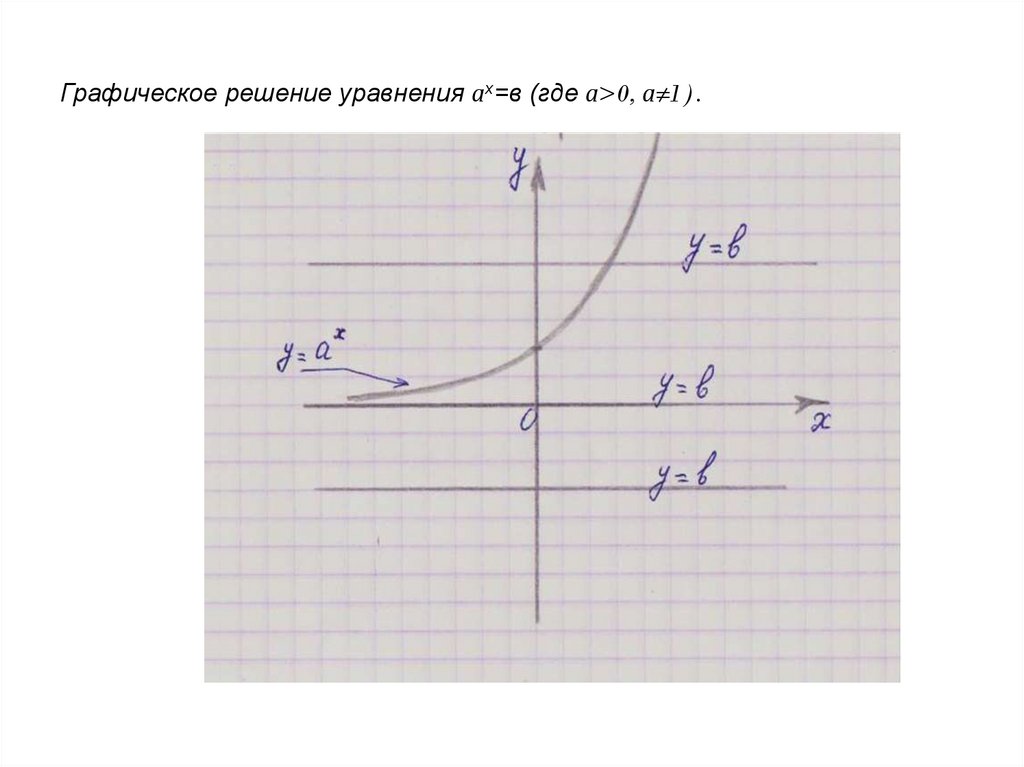
8. Графическое решение уравнения ах=в (где а>0, а≠1).
Графическое решение уравнения ах=в (где а>0, а≠1).9. Уравнение ах=b
Уравнениех
а =b
имеет единственный корень при а>0, а≠1, b>0.
Для того, чтобы его найти, надо b представить в виде
b=ас.
Получаем: ах=ас
х=с
Решение показательного уравнения вида: 1).аf(х)=аg(х)(где
а>0,а≠1) основано на том, что это уравнение равносильно
уравнению f(х)=g(х).
2) аf(х)=1 сводится к уравнению
f(х)=0, где f(х)-функция, определённая на множестве R
10. Решить уравнение 32-х-6·32х=32х+1.
Решение32-х-6·32х=32х+1
32-х-6·32х=3·32х
32-х=6·32х+3·32х
32-х=9·32х
32-х=32х+2
2-х=2х+2
3х=0
Х=0
32-6·30=30+1
9-6=3
Ответ:х=0.
11. Решить уравнение 4х-5·2х+4=0.
• Решение.4х-5·2х+4=0
22х-5·2х+4=0
4х=(22)х=(2х)2
Пусть t=2х, тогда
t2-5t+4=0
t1=1, t2=4
Сделаем обратную замену
2х=1
2х=4
х=0
х=2
Ответ:0;2.
12. Задание на дом:
• П.36 (1), решить с №460 (а,б) по№464(а,б).










 mathematics
mathematics