Similar presentations:
Приёмы устного решения квадратного уравнения. Подготовка к экзаменам в тестовой форме
1.
Приёмы устного решенияквадратного уравнения.
Подготовка к
экзаменам в тестовой
форме
Романова О.В.
учитель математики
2.
Цели урока• Обобщить и систематизировать изученный материал
по теме: «Квадратные уравнения».
• Научить учащихся приёмам устного решения
квадратных уравнений.
•Обучать поискам нескольких способов решения одной
задачи и умению выбирать из них наиболее оригинальный ,
оптимальный
• Развивать внимание и логическое мышление.
3.
Человеку, изучающему алгебру, часто полезнее решитьодну задачу тремя различными способами, чем решать
три-четыре различные задачи.
Решая одну задачу различными способами, можно путем
сравнения выяснить, какой из них короче и эффективнее.
Так вырабатывается опыт.
У.У. Сойер
4. Впервые ввёл термин «квадратное уравнение» немецкий философ Кристиан Вольф Сильвестр Джеймс Джозеф - английский математик, ввел
«Уравнение - это золотой ключ, открывающий всематематические сезамы».
С. Коваль.
ВПЕРВЫЕ ВВЁЛ ТЕРМИН «КВАДРАТНОЕ УРАВНЕНИЕ» НЕМЕЦКИЙ
ФИЛОСОФ КРИСТИАН ВОЛЬФ
СИЛЬВЕСТР ДЖЕЙМС ДЖОЗЕФ - АНГЛИЙСКИЙ МАТЕМАТИК, ВВЕЛ
СЛОВО «ДИСКРИМИНАНТ»
5.
Вопросытеоретической разминки
1.
Какое уравнение называется квадратным?
ах2 + вх + с = 0
2. Объясните, в чём заключается смысл ограничения
в определении квадратного уравнения (а ≠ 0).
3. Какое квадратное уравнение называется
неполным?
4. Какое квадратное уравнение называется
приведённым?
х2 + рх + q = 0
5. Назовите вид квадратных уравнений:
а) 2 ²-5х +10=0;
б) ²+ =0;
в) 6 ²-5=0;
г) ² - 4 + 3 = 0
д) 5 ²-4 =3;
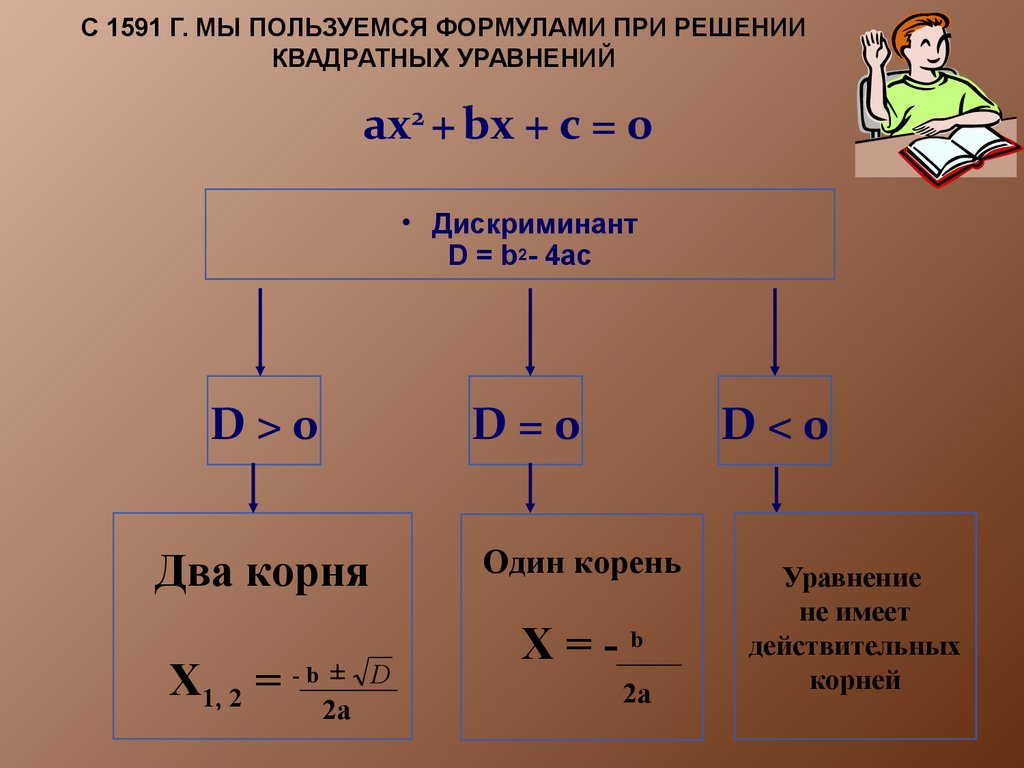
6. С 1591 г. мы пользуемся формулами при решении квадратных уравнений
С 1591 Г. МЫ ПОЛЬЗУЕМСЯ ФОРМУЛАМИ ПРИ РЕШЕНИИКВАДРАТНЫХ УРАВНЕНИЙ
ах2 + bх + с = 0
• Дискриминант
D = b2- 4ac
D>0
D=0
Один корень
Два корня
Х1, 2 = - b ±
2а
D<0
D
Х=-b
2а
Уравнение
не имеет
действительных
корней
7.
Франсуа Виет(1540-1603)Именно этим французским математиком
впервые
были
введены
буквенные
обозначения.
До
этого
пользовались
громоздкими словесными формулировками.
Например
x2 + 24 = 11x
«Квадрат и число 24 равны одиннадцати
корням»
Формулы,
выражающие
зависимость
корней от его коэффициентов, были
выведены Виетом в 1591г.
8. Теорема Виета
ТЕОРЕМА ВИЕТАx1 , x2 корни
уравнения
2
x px g 0
x1 x2
x1 x2 g
p
9.
Приёмы устногорешения квадратного
уравнения
2
ax bx c 0
Приём «Коэффициентов»:
1) Если а+в+с=0, то
x 1 1, x 2
2) Если в = а + с, то
x1 1, x2
3) Если
a b c 0
c
.
a
c
.
a
, то приём «Переброски»
Используя приёмы 1) -3) можно придумывать
уравнения с рациональными корнями.
10.
4)5)
6)
7)
ax 2 ( a 2
x1 a
1) x a 0
x 2 1
a
ax 2 ( a 2
x1 a
1) x a 0
x2 1
a
ax 2 ( a 2
x1 a
1) x a 0
x2 1
a
ax 2 ( a 2
x1 a
1) x a 0
x 2 1
a
11.
К какому типу относится уравнениеРешите его
1) Если а+в+с=0, то
x 1 1, x 2
c
.
a
1)
2) Если в = а + с, то
x1 1, x2
3)
4)
x1 a
ax (a 1) x a 0
x2 1
a
5)
x1 a
ax (a 1) x a 0
x2 1
a
6)
x1 a
ax 2 (a 2 1) x a 0
x 2 1
a
2
17 x 288 x 17 0,
c
.
a
x1 a
ax 2 (a 2 1) x a 0
x 2 1
a
2
2
2)
10 x 2 99 x 10 0
3) 2 x 2 x 3 0
x1 17
x2 1
17
x1 10
x2 1
10
1;
3
2
2
4)
4x
2
11x 7 0
x1 1, x2
7
4
2
5) 8 х2 - 65 х + 8 = 0
Х1=8; Х2=1/8
6) 5 х2 + 26 х + 5 = 0
Х1= -5; Х2= -1/5
12.
Приём «Переброски»Если
Пример:
1. Умножим а на с :
a b c 0
2 x 2 11x 5 0
2 x 2 11x 5 0
2. Получим новое приведенное квадратное уравнение :
2
x 11x 10 0
3. Используя теорему Виета, находим его корни 10 и 1,
и делим на 2.
Ответ: 5; 1/2
13.
Решаем, используя метод«переброски»
2
6 x 7 x 3 0
Получим уравнение
2
x 7 x 18 0
Корни 9 и (-2).
Делим числа 9 и ( -2) на 6:
3
1
;
Ответ :
2
3
9
2
x1 , x 2
6
6
14.
Задачи на квадратные уравнениявстречаются уже в 499 г.
В древней Индии были
распространены публичные
соревнования в решении трудных
задач.
В одной из старинных индийских
книг говорится по поводу таких
соревнований следующее:
«Как солнце блеском своим
затмевает звезды, так ученый
человек затмит славу другого в
народных собраниях, предлагая и
решая алгебраические задачи».
Часто они были в стихотворной
форме. Вот одна из задач
знаменитого индийского
математика XII века.
Задача Бхаскары
15.
2ax bx c 0
b = 2k (чётное число)
D1
b
2
2
ac
b
D1
х1,2 2
a
Решение:
Пусть x – число обезьян, тогда
(х/8)2 + 12 = х,
х2/64 - х + 12 = 0,
х2 - 64х + 768 = 0.
D1 = 1024 - 768 = 256,
х1 = 16, х2 = 48.
Ответ: 16 или 48.
16.
Выводы:• данные приёмы решения заслуживают внимания,
поскольку они не отражены в школьных учебниках
математики;
• овладение данными приёмами поможет учащимся
экономить время и эффективно решать уравнения;
• потребность в быстром решении обусловлена
применением тестовой системы выпускных экзаменов.
17.
Подведение итоговНаш урок подходит к концу, подумайте о том с какой
пользой для вас прошёл этот урок.
Ответьте на вопрос или закончите предложения
-Сегодня я узнал…
-Теперь
я могу…
-Материал урока мне был…
-Как вы могли бы оценить свою
работу на уроке?
















 mathematics
mathematics








