Предел функции

1. Математический анализ не менее всеобъемлющ, чем сама природа; он определяет все ощутимые взаимосвязи, измеряет времена,

пространства, силы,
температуры.
Ж. Фурде

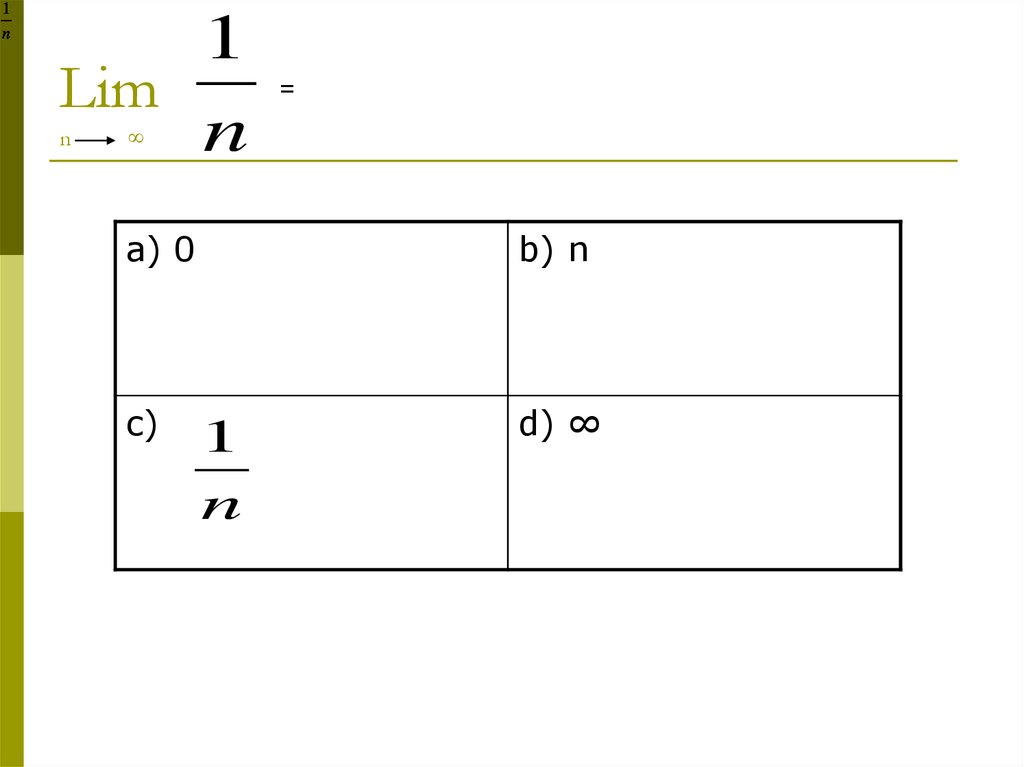
2. Lim n ∞

1
n
1
Lim
n
n
=
∞
a) 0
c)
b) n
1
n
d) ∞

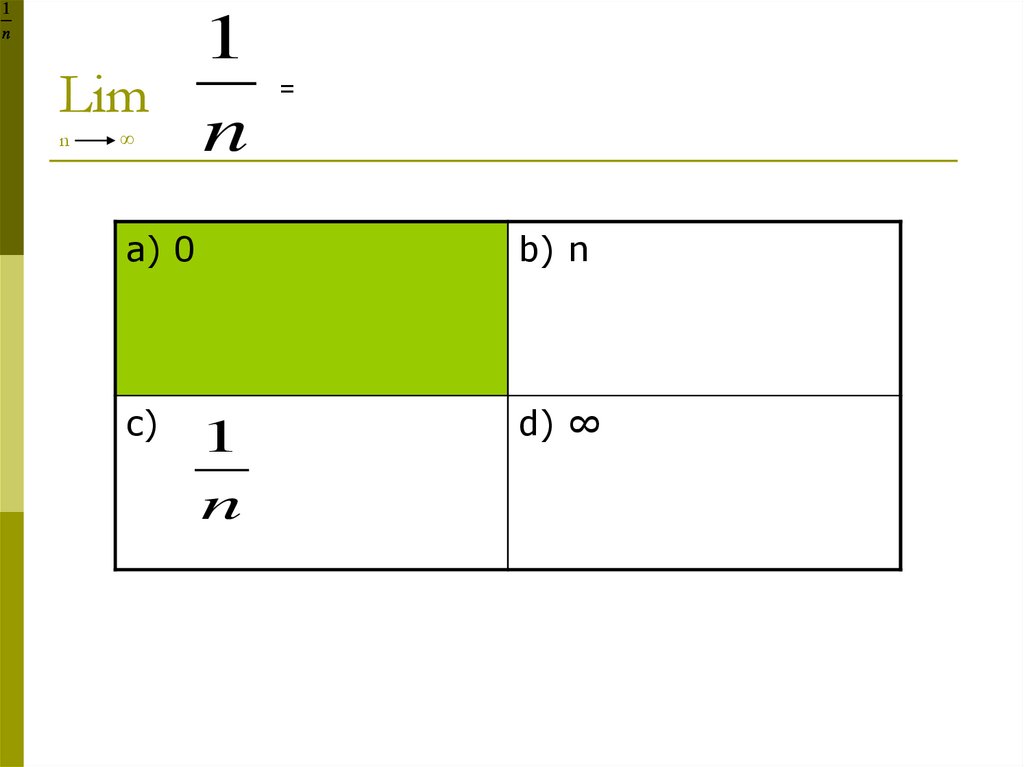
3. Lim n ∞

1
n
1
Lim
n
n
=
∞
a) 0
c)
b) n
1
n
d) ∞

4. Lim n ∞

1
n
Lim
n
qn
=
∞
a) q
b) n
c) 0
d) ∞

5. Lim n ∞

1
n
Lim
n
qn
=
∞
a) q
b) n
c) 0
d) ∞

6. Lim n ∞

1
n
Lim
n
C=
∞
a) 0
b) c
c) 1
d) ∞

7. Lim n ∞

1
n
Lim
n
C=
∞
a) 0
b) c
c) 1
d) ∞

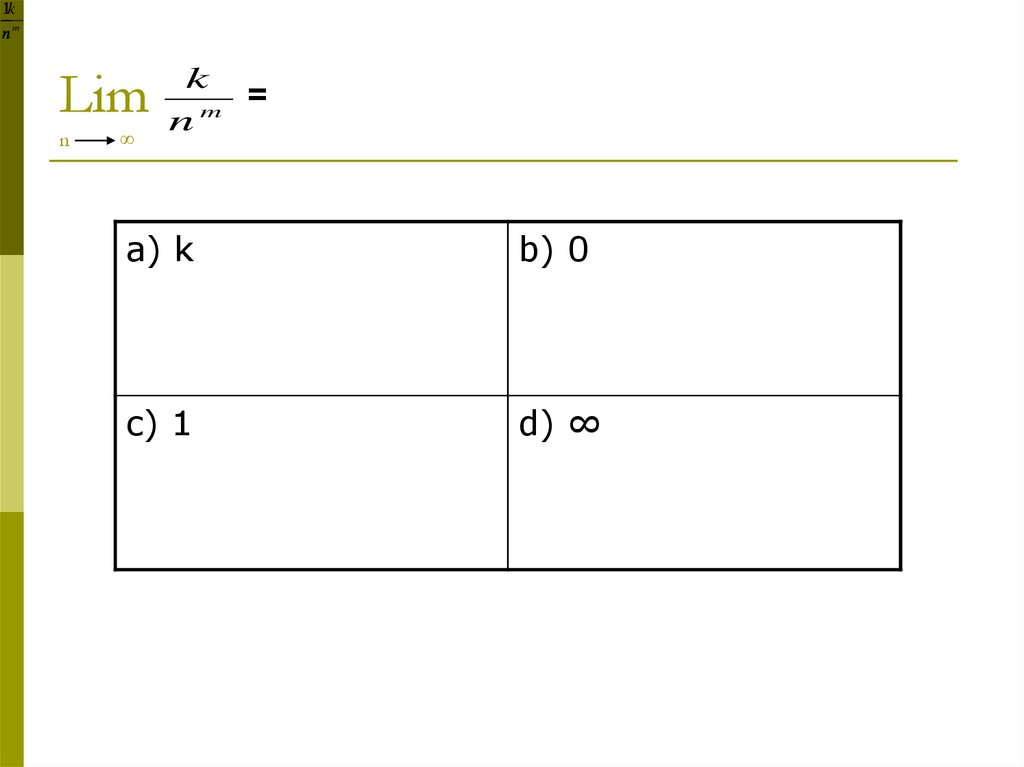
8. Lim n ∞

1k
nm
Lim
n
∞
k
=
m
n
a) k
b) 0
c) 1
d) ∞

9. Lim n ∞

1k
nm
Lim
n
∞
k
=
m
n
a) k
b) 0
c) 1
d) ∞

10. Lim(xn + yn) = n ∞

1k
nm
Lim(xn + yn) =
n
∞
a) Lim(xn )+Lim( yn)
n
∞
n
∞
c) 1Lim(xn )∙Lim( yn)
n
∞
n
b) 0
∞
d) ∞

11. Lim(xn + yn) = n ∞

1k
nm
Lim(xn + yn) =
n
∞
a) Lim(xn )+Lim( yn)
n
∞
n
∞
c) 1Lim(xn )∙Lim( yn)
n
∞
n
b) 0
∞
d) ∞

12. Lim(xn • yn) = n ∞

1k
nm
Lim(xn • yn) =
n
∞
a) Lim(xn )+Lim( yn)
n
∞
n
∞
c) 1Lim(xn )∙Lim( yn)
n
∞
n
b) 0
∞
d) ∞

13. Lim(xn • yn) = n ∞

1k
nm
Lim(xn • yn) =
n
∞
a) Lim(xn )+Lim( yn)
n
∞
n
∞
c) 1Lim(xn )∙Lim( yn)
n
∞
n
b) 0
∞
d) ∞

14. Lim(xn / yn) = n ∞

1k
nm
Lim(xn / yn) =
n
∞
a) Lim(xn )-Lim( yn)
n
∞
n
∞
c) 1Lim(xn )∙Lim( yn)
n
∞
n
b) 0
∞
d) Lim(xn )/Lim( yn)
n→∞
n→∞

15. Lim(xn / yn) = n ∞

1k
nm
Lim(xn / yn) =
n
∞
a) Lim(xn )-Lim( yn)
n
∞
n
∞
c) 1Lim(xn )∙Lim( yn)
n
∞
n
b) 0
∞
d) Lim(xn )/Lim( yn)
n→∞
n→∞

16. Lim(kxn) = n ∞

1k
nm
Lim(kxn) =
n
∞
a) Lim(xn )
n
b) kxn
∞
c) k Lim(xn )
n
∞
d) k

17. Lim(kxn) = n ∞

1k
nm
Lim(kxn) =
n
∞
a) Lim(xn )
n
b) kxn
∞
c) k Lim(xn )
n
∞
d) k

18.

5
е
-9
л
4
н
20
ц
3
п
6
ф
0
р
-20 -5
у
д
1 вариант
1. Lim 3 = 3
(П)
2 ВАРИАНТ
Lim 6 = 6
n→∞
2. Lim 2 = 0
(Р)
n
n→∞
3. Lim (1/n + 5) = 5 ( Е )
n→∞
4. Lim (1/n – 5) = -5 ( Д )
n → ∞ 5
5. Lim 1 = 5
(Е)
1
n → ∞ n
1.
6. Lim (-9 + ( 1/3)n )= -9 ( Л )
n→∞
6. Lim ( 2 1 ) = 1
n n
n→∞
1
7. Lim (1 – ( ) n ) = 1
( Ф)
n→∞
2. Lim ( -20) = -20
n→∞
3. Lim (( 1 ) N 4) = 4
n→∞ 2
7
4. Lim 2
=7
n
1
n→∞
5. Lim (2•10) = 20
n→∞
2
n→∞
5
2
( У)
(Н)
(к)
(ц )
(и)
(и)
7
к
1
и

19. Тема урока:

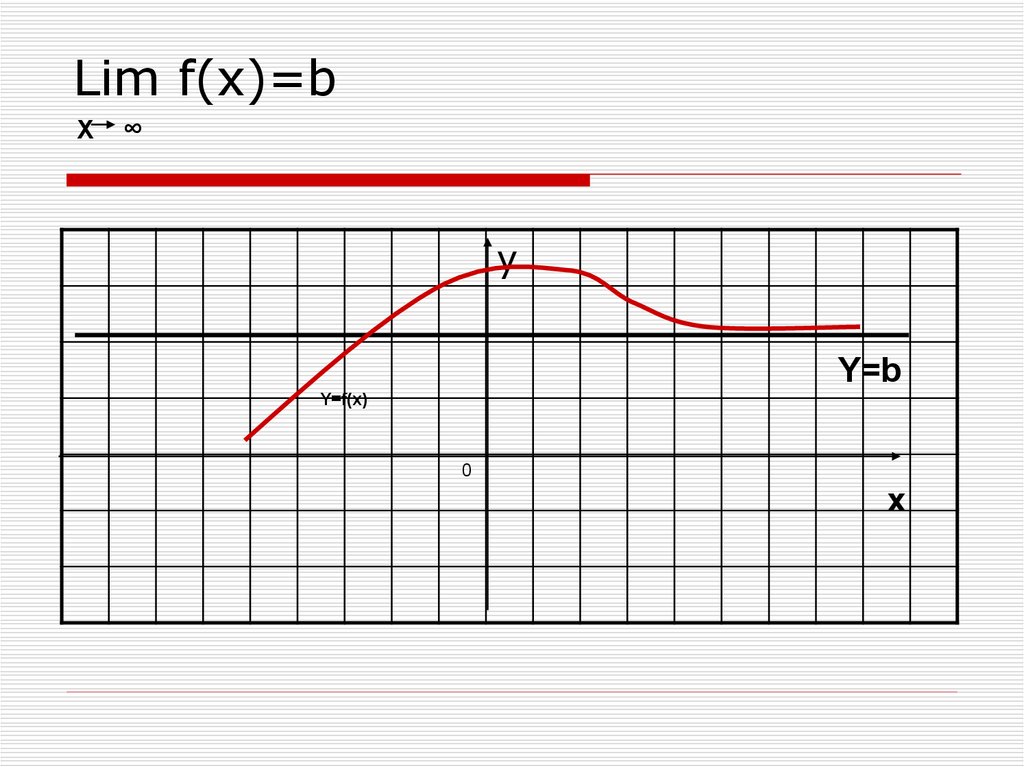
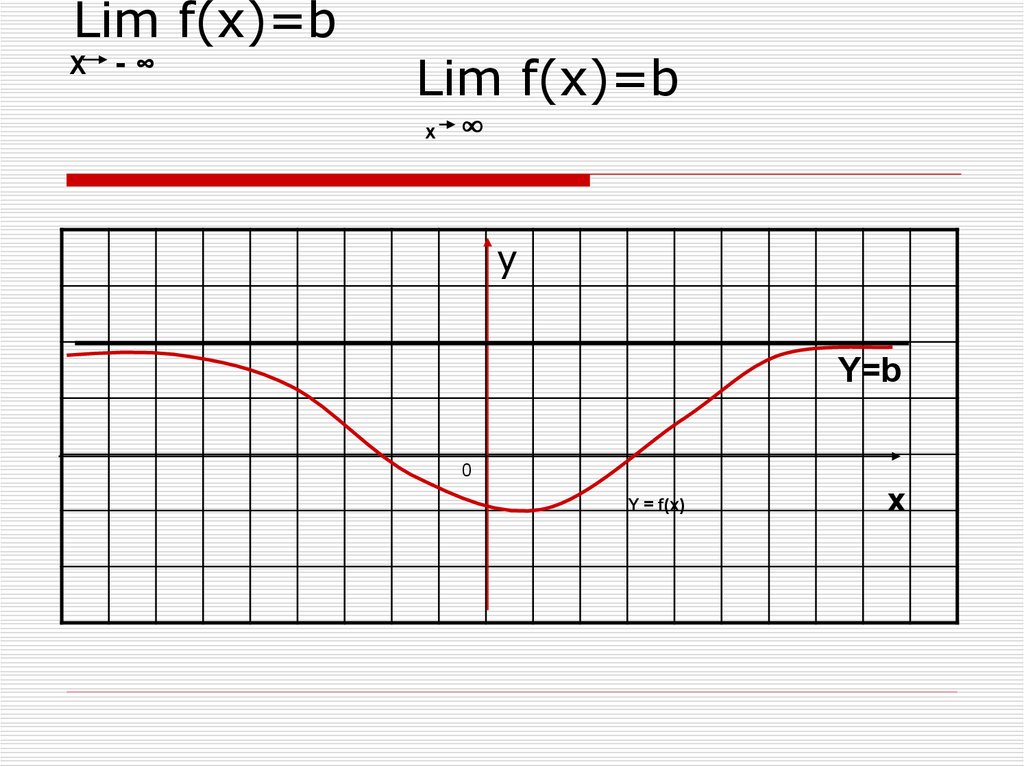
20. Lim f(x)=b

X
∞
y
Y=b
Y=f(x)
0
x

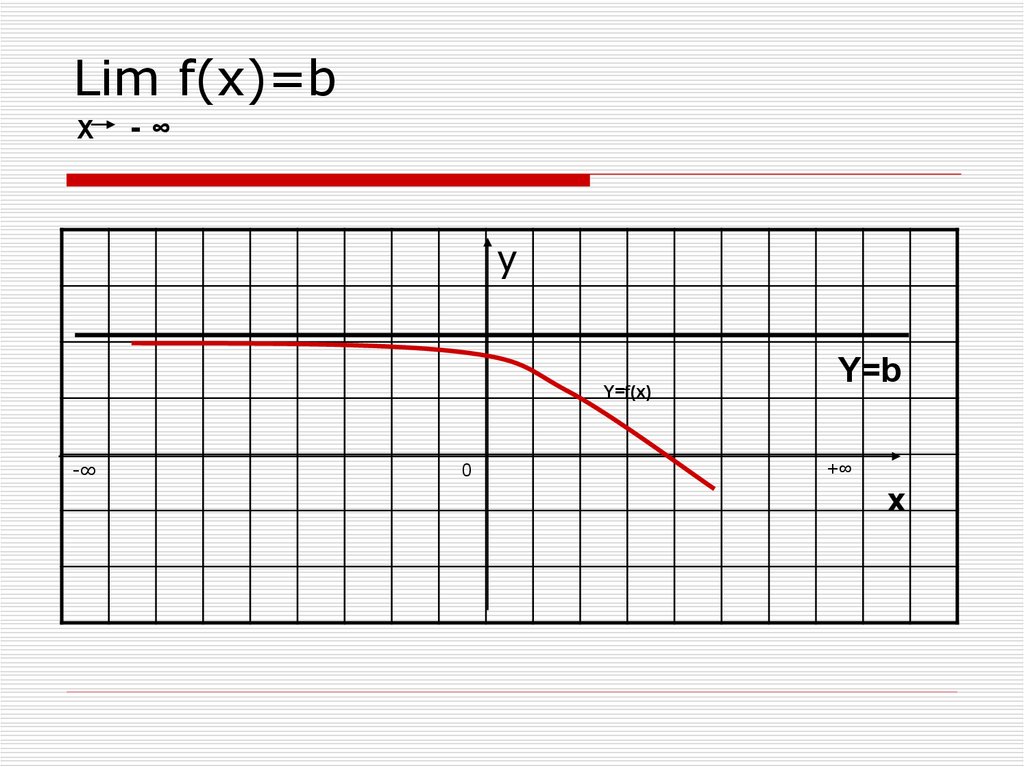
21. Lim f(x)=b

X
-∞
y
Y=f(x)
-∞
0
Y=b
+∞
x

22. Lim f(x)=b Lim f(x)=b

Lim f(x)=b
X
-∞
Lim f(x)=b
x
∞
y
Y=b
0
Y = f(x)
x

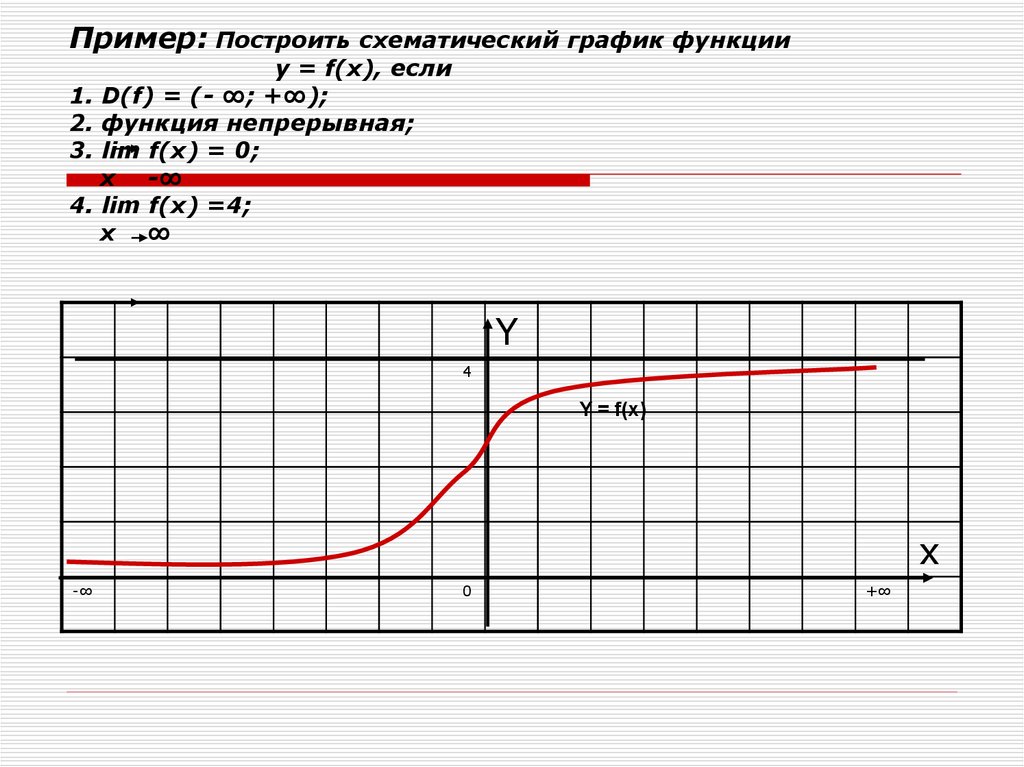
23. Пример: Построить схематический график функции у = f(x), если 1. D(f) = (- ∞; +∞); 2. функция непрерывная; 3. lim f(x) = 0; x

Пример: Построить
1.
2.
3.
4.
схематический график функции
у = f(x), если
D(f) = (- ∞; +∞);
функция непрерывная;
lim f(x) = 0;
x -∞
lim f(x) =4;
x ∞
Y
4
Y = f(x)
x
-∞
0
+∞

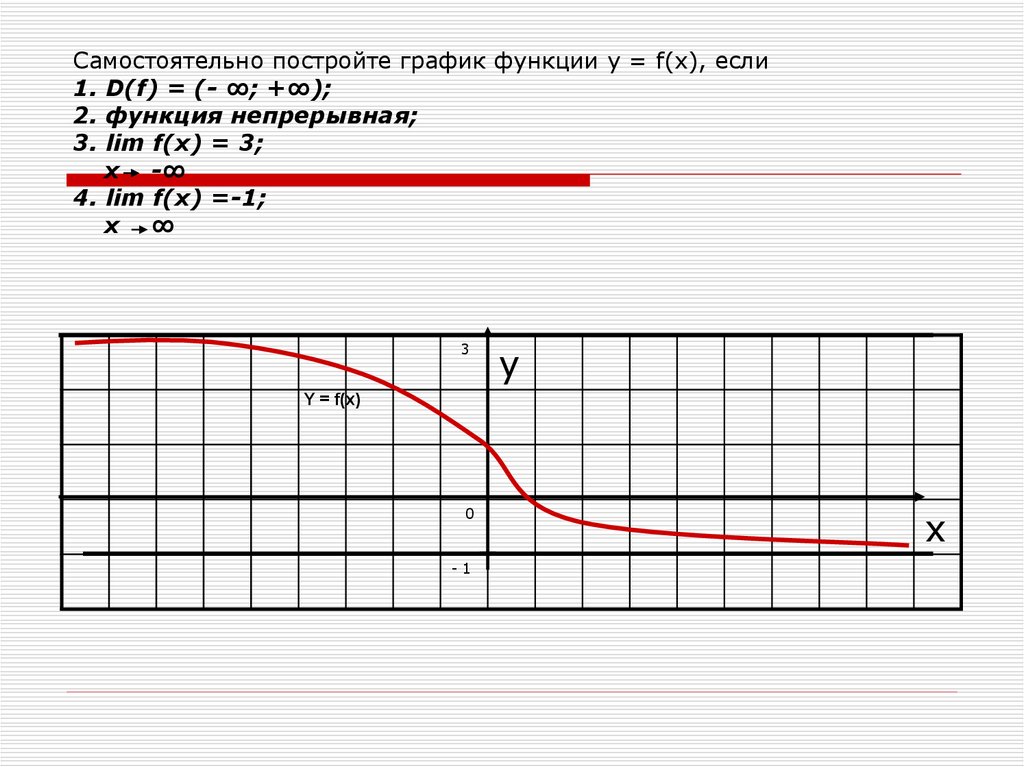
24. Самостоятельно постройте график функции у = f(x), если 1. D(f) = (- ∞; +∞); 2. функция непрерывная; 3. lim f(x) = 3; x -∞ 4.

lim f(x) =-1;
x ∞
3
0
-1
y
х

25. Самостоятельно постройте график функции у = f(x), если 1. D(f) = (- ∞; +∞); 2. функция непрерывная; 3. lim f(x) = 3; x -∞ 4.

lim f(x) =-1;
x ∞
3
y
Y = f(x)
0
-1
х

26.

• 1. lim(1/xm ) = 0, где m - натуральное число;
∞
X
2. lim ( f(x) + g(x)) = lim f(x) + lim g(x) ;
X
∞
X
∞
X
∞
3. lim f(x) • g(x) = lim f(x) • lim g(x) ;
X
∞
X
∞
X
∞
4. lim (f(x)/ g(x)) = lim f(x) / lim g(x) ;
X
∞
X
∞
X
∞
5. Lim k f(x) =k lim f(x)
X
∞
X
∞

27. Домашнее задание:

• Выучить формулы.
• §26, № 26.3