Transportation problem. (Lecture 6)

1.

National Aviation University
Department of Airnavigation system
Lecture 6: Transportation problem
Content of lecture:
1. Building of mathematical model of transportation
problem
2. Method of potentials
3. Task about oranges, cars, aircrafts
Professor Shmelova T.

2.

Transportation problem applications
Task 1 - about oranges
Task 2 - about cars
Task 3 - about Aircraft

3.

4.

1. Building of mathematical model of transportation
problem
Transportation problem – is a special class of linear problem that
deals with shipping a commodity from sources (e.g. factories,
departure point,..) to destinations (e.g. warehouses).
Transportation problem (logistic) – is a special class of linear tasks
that deals with transportation cargo from sources to destinations
with minimal cost
The objective is to determine the shipping schedule that minimizes
the total shipping cost while satisfying supply and demand limits.
The application of the transportation model can be extended to other areas of
operation, including
• inventory control (management) (управление запасами),
• employment scheduling (планирование),
• distribution of resources (распределение ресурсов);
• personal assignment (назначение персонала)
• Logistics

5.

Graphical interpretation of TP:
Mathematical model of Transport task,
m
n
i 1 j 1
n
x
j 1
m
x
i 1
ij
ij
cij x ij min;
ai, i=1,2,…,m;
bj, j=1,2,…,n;
xij 0,
i=1,2,…,m; j=1,2,…,n.

6.

7.

Method of decision Transportation problem:
• Simplex method as method of LP
• Method of potentials
• Excel
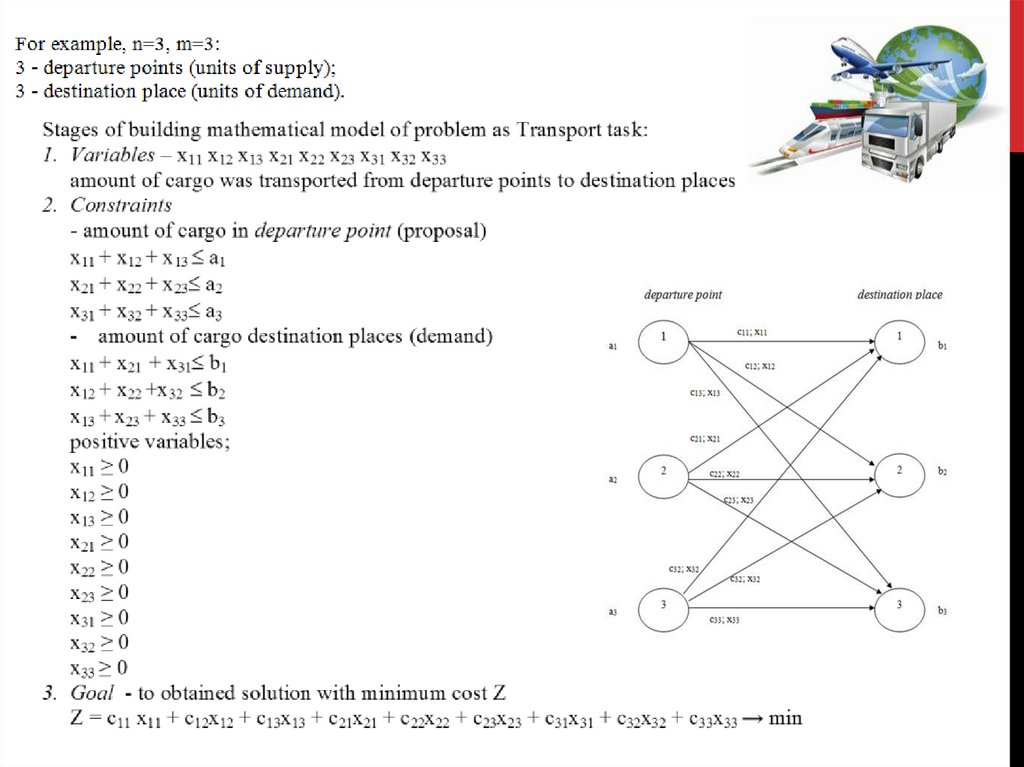
Stages of building mathematical model of Transportation problem:
1. Variables – xij - amount of cargo was transported from i - departure point to j- destination
place, i=1,…m; j=1,….n
2. Constraints - amount of cargo in i - departure point (proposal) - ai and in j- destination
place (demand) - bj. , i=1,…m; j=1,….n
n
x
j 1
ij
m
x
i 1
ij
ai, i=1,2,…,m;
bj, j=1,2,…,n;
3. Goal – to obtained optimal solution for transportations from all departure point to all
destination place with minimum cost (maximum profit)
m
n
i 1 j 1
Criteria - minimum cost (maximum profit)
c ij x ij min

8.

9.

Mathematical model Mathematical model of our transport task (main type):

10.

If the condition is satisfy:
n
m
a
i 1
i
=
b
j 1
j
,
we have closed (balanced) transport task
If the condition is not satisfied, we must to add fictitious arcs
m
a
i 1
i
m
a
i 1
i
≥
n
b
j 1
≤
j
n
b
j 1
j
→
a
i 1
→
n
m
i
=
b
j 1
n
m
a
i 1
+ bi0
j
i
+ a0j =
b
j 1
j
Methods of design
- Simplex-method as linear programming solution
- Excel
- method of potentials

11.

2. Method of potentials
Potential method first proposed Kantorovich in 1949.
Later, a similar method developed by G. Dantzig, based on the general
ideas of LP.
1.
Algorithm of Method of potentials
Make a a transport table
2. Find the basic solution transport problem with one of the methods,
such as:
• method northwest corner;
• the method of least cost
3. Check the basic solution for optimality
4. If the solution is not optimal - Recalculate the new reference solution
in accordance with rule

12.

13.

3. Tasks
Task 1 - about oranges
To be transported oranges with vegetable bases A and B in
stores 1, 2, and 3.
bases
From vegetable base A – 10 tons
From vegetable base B – 20 tons
To shop №1 - 7 tons
To shop №2 - 12 tons
To shop №3 – 11tons
Cost of transportations 1 ton of cargo
in table
To obtain solution with minimum cost Z
shops

14.

Cost of transportations 1 ton of cargo in table
Bases / shops
1
2
3
Proposal
Cost
A
3
6
5
10
B
8
10
9
20
Demand
7
12
11

15.

16.

1. Make a transport table
1
2
3
Proposal
potentials
shops
bases
А
3
7
В
3
8
10
potentials
7
v1
u1
10
9
Demand
5
6
11
12
v2
u2
9
20
11
v3
2. Find the basic solution transport problem with one of
the methods, such as:
• method northwest corner:

17.

1
2
3
Proposal
shops
bases
А
3
7
В
6
8
10
9
Demand
5
10
u1
9
20
u2
3
7
V1
11
12
V2
11
V3

18.

1
2
3
Proposal
shops
bases
А
3
7
В
6
5
10
u1
10
9
20
u2
3
8
9
Demand
7
11
12
11

19.

Optimal solution:
Shipping:
Bases:
A
B
Shops:
N1
N2
N3
10 = 7+ 5
20 = 9 + 11
7 =7
12 = 5 + 9
11 = 11

20.

To obtained solution with using Excel
имя
значение
нижн.гр.
вер.гр.
коэф.в ЦФ
x11
Переменные
x13
x21
x12
7
3
0
x22
0
x23
9
11
ЦФ
3
вид
1
0
1
0
0
6
5
Ограничения
коэффициенты
1
1
0
0
0
0
1
0
0
1
8
0
1
1
0
0
10
0
1
0
1
0
9
228
лев.часть знак
0
10
=
1
20
=
0
7
=
0
12
=
1
11
=
пр.часть
10
20
7
12
11

21.

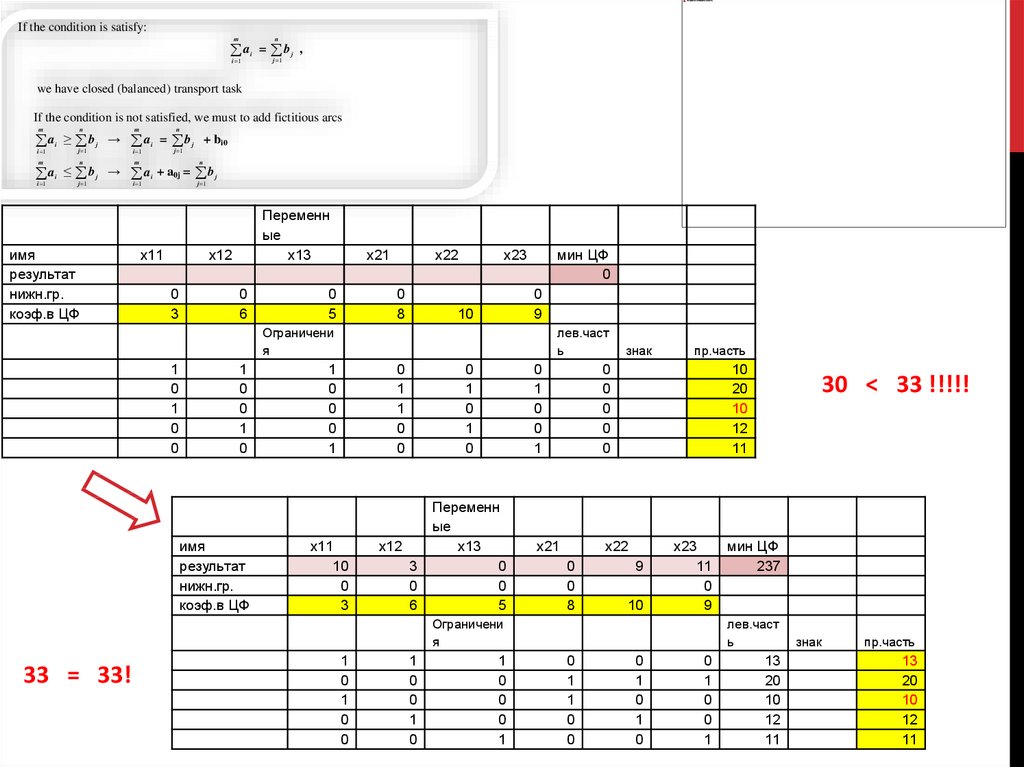
If the condition is satisfy:
n
m
a
i 1
i
=
b
j 1
j
,
we have closed (balanced) transport task
If the condition is not satisfied, we must to add fictitious arcs
m
a
i 1
i
≥
i
≤
m
a
i 1
n
b
j 1
j
→
j
→
n
b
j 1
n
m
a
i 1
=
b
j 1
i 1
+ bi0
j
n
m
a
имя
результат
нижн.гр.
коэф.в ЦФ
i
i
+ a0j =
x11
b
j 1
j
Переменн
ые
x13
x12
0
3
0
6
x21
0
5
x22
0
8
x23
мин ЦФ
0
0
9
10
Ограничени
я
1
0
1
0
0
1
0
0
1
0
имя
результат
нижн.гр.
коэф.в ЦФ
лев.част
ь
1
0
0
0
1
0
1
1
0
0
x11
10
0
3
0
1
0
1
0
x12
3
0
6
Переменн
ые
x13
0
0
5
знак
0
1
0
0
1
0
0
0
0
0
x21
x22
0
0
8
пр.часть
10
20
10
12
11
9
10
x23
11
0
9
Ограничени
я
33 = 33!
1
0
1
0
0
1
0
0
1
0
1
0
0
0
1
30 < 33 !!!!!
мин ЦФ
237
лев.част
ь
0
1
1
0
0
0
1
0
1
0
0
1
0
0
1
13
20
10
12
11
знак
пр.часть
13
20
10
12
11

22.

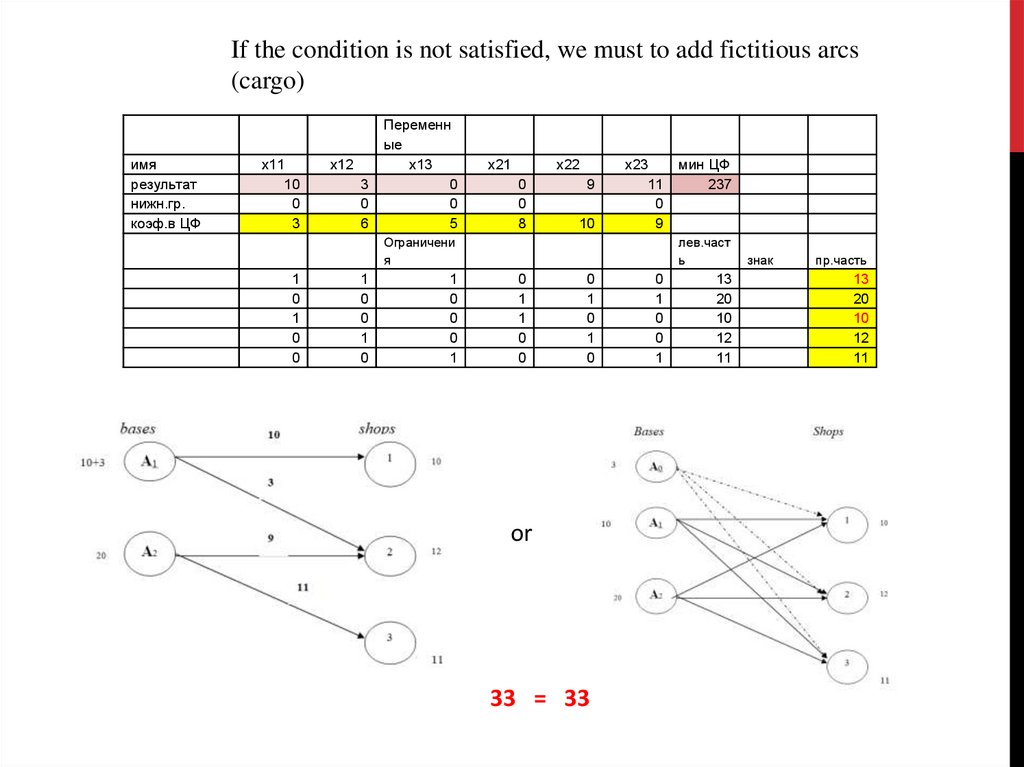
If the condition is not satisfied, we must to add fictitious arcs
(cargo)
имя
результат
нижн.гр.
коэф.в ЦФ
x11
10
0
3
x12
3
0
6
Переменн
ые
x13
0
0
5
x21
x22
0
0
8
9
10
x23
11
0
9
Ограничени
я
1
0
1
0
0
1
0
0
1
0
1
0
0
0
1
мин ЦФ
237
лев.част
ь
0
1
1
0
0
0
1
0
1
0
or
33 = 33
0
1
0
0
1
13
20
10
12
11
знак
пр.часть
13
20
10
12
11

23.

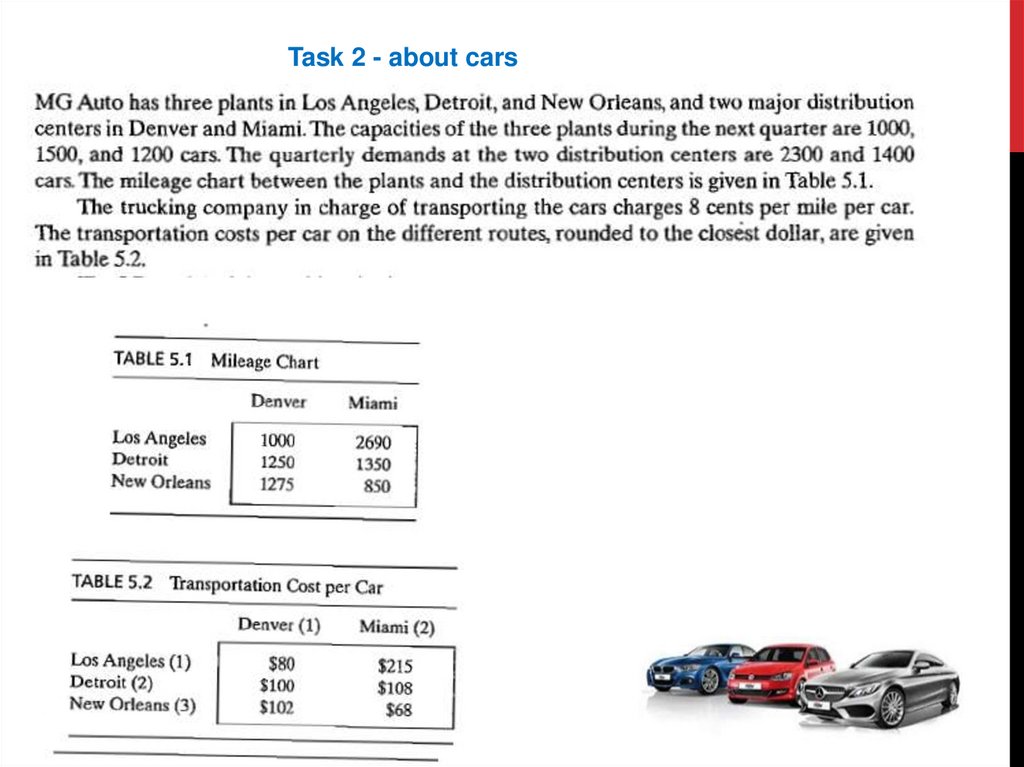
Task 2 - about cars

24.

Model

25.

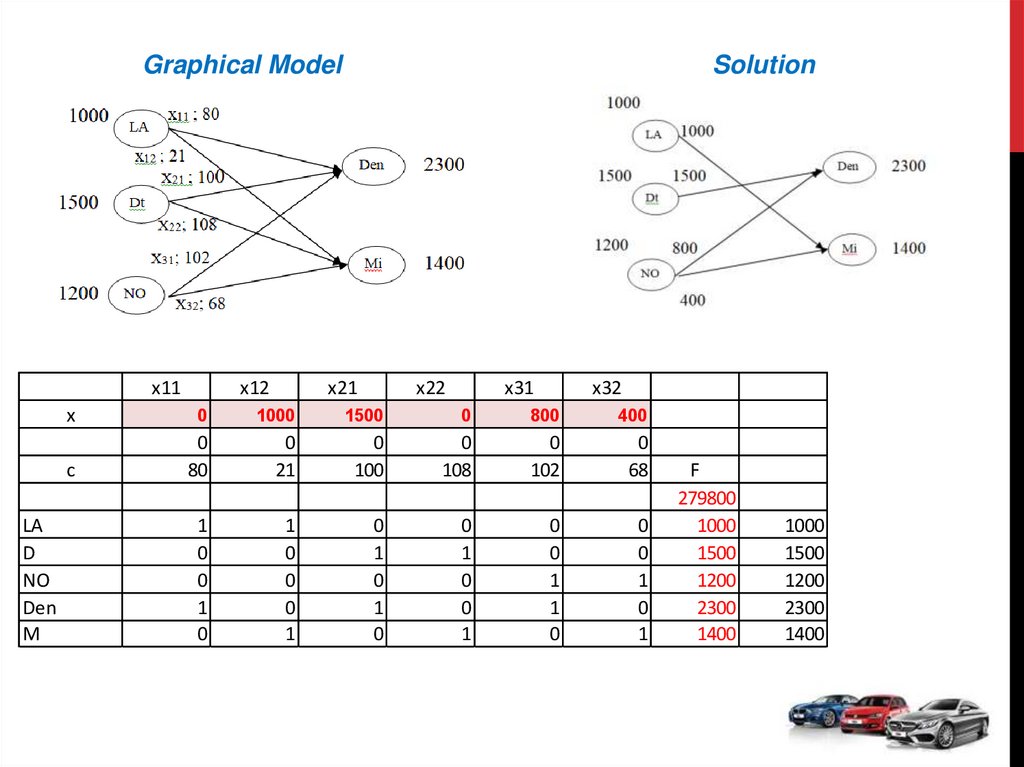
Graphical Model
x11
LA
D
NO
Den
M
x12
Solution
x21
x22
x31
x32
x
0
1000
1500
0
800
400
c
0
80
0
21
0
100
0
108
0
102
0
68
1
0
0
1
0
1
0
0
0
1
0
1
0
1
0
0
1
0
0
1
0
0
1
1
0
0
0
1
0
1
F
279800
1000
1500
1200
2300
1400
1000
1500
1200
2300
1400

26.

Task 3 - about Aircraft
Приклад оптимізації транспортних потоків
авіакомпанії, яка має літаки типів
• Б-737-200,
• Б-737-400,
• Б-767-300ER
та виконує рейси за маршрутами
• Київ – Афіни,
• Київ – Ашхабад,
• Київ – Будапешт,
• Київ – Варшава.
Тип ВС
1
2
3
Прогнозируемый
пассажиропоток
маршрутах
Авиалинии
Транспортные расходы
1
2
3
15
20
25
70
28
15
40
70
40
3000 500
3000
Число
ВС Вместимость
каждого типа
ВС
4
40
45
65
200
10
20
30
100
200
150
на
An example of an airline's traffic flow optimization, which has aircraft type
Boeing-737-200, Boeing-737-400, Boeing-767-300ER and performs flights on
routes: Kiev-Athens, Kiev-Ashgabat, Kiev-Budapest, Kiev-Warsaw.

27.

Model

28.

Solution
имя
значение
нижн.гр.
вер.гр.
коэф.в ЦФ
x11
5
0
15
x12
x13
x14
x21
x22
x23
x24
x31
x32
x33
x34
5
0
0
0
0
0
0
0
0
0
19
0
1
0
30
0
0
0
0
0
0
0
20
25
40
70
28
15
45
40
70
40
65
вид
1
0
0
100
0
0
0
1
0
0
0
100
0
0
1
0
0
0
0
100
0
1: 5*100+30*150=5000
2: 5*100=500
3: 19*200=3800
4: 200
1
0
0
0
0
0
100
0
1
0
200
0
0
0
0
1
0
0
200
0
0
0
1
0
0
0
200
0
0
1
0
0
0
0
200
0
0
1
150
0
0
0
0
0
1
0
150
0
0
0
0
1
0
0
150
0
ЦФ
1705
левая
ч.
знак
0
10
0
20
1
30
0 5000
0
500
0 3800
150
200
прав ч.
10
20
30
3000
500
3000
200

29.

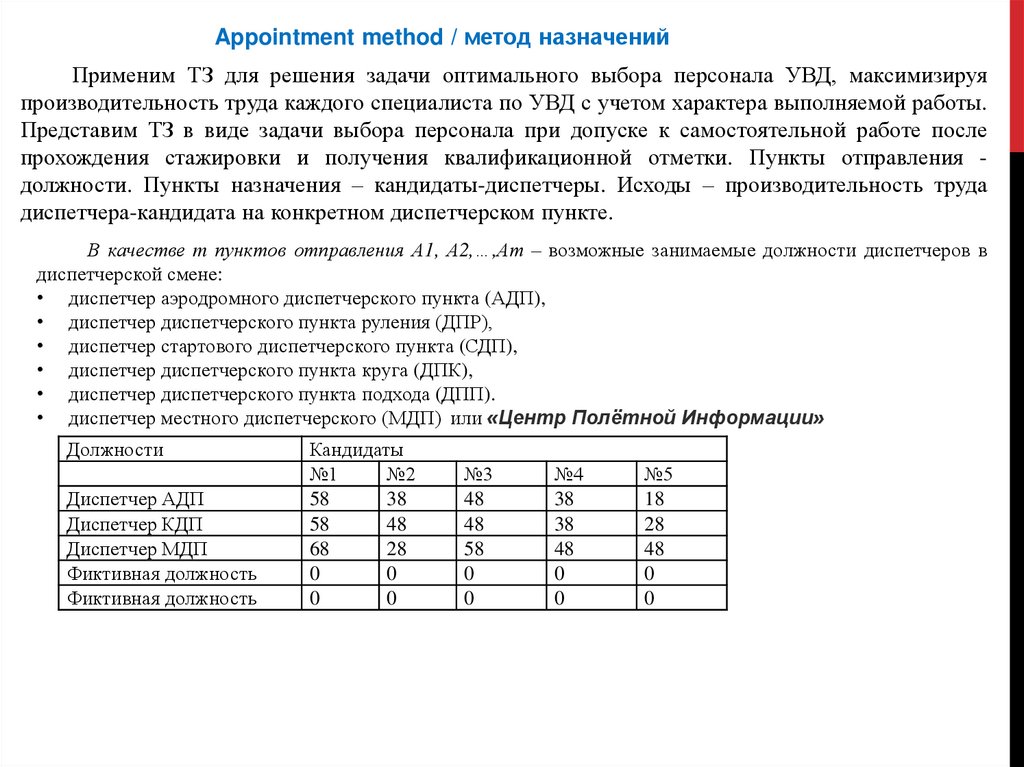
Appointment method / метод назначений
Применим ТЗ для решения задачи оптимального выбора персонала УВД, максимизируя
производительность труда каждого специалиста по УВД с учетом характера выполняемой работы.
Представим ТЗ в виде задачи выбора персонала при допуске к самостоятельной работе после
прохождения стажировки и получения квалификационной отметки. Пункты отправления должности. Пункты назначения – кандидаты-диспетчеры. Исходы – производительность труда
диспетчера-кандидата на конкретном диспетчерском пункте.
В качестве m пунктов отправления А1, А2,…,Аm – возможные занимаемые должности диспетчеров в
диспетчерской смене:
• диспетчер аэродромного диспетчерского пункта (АДП),
• диспетчер диспетчерского пункта руления (ДПР),
• диспетчер стартового диспетчерского пункта (СДП),
• диспетчер диспетчерского пункта круга (ДПК),
• диспетчер диспетчерского пункта подхода (ДПП).
• диспетчер местного диспетчерского (МДП) или «Центр Полётной Информации»
Должности
Диспетчер АДП
Диспетчер КДП
Диспетчер МДП
Фиктивная должность
Фиктивная должность
Кандидаты
№1
№2
58
38
58
48
68
28
0
0
0
0
№3
48
48
58
0
0
№4
38
38
48
0
0
№5
18
28
48
0
0

30.

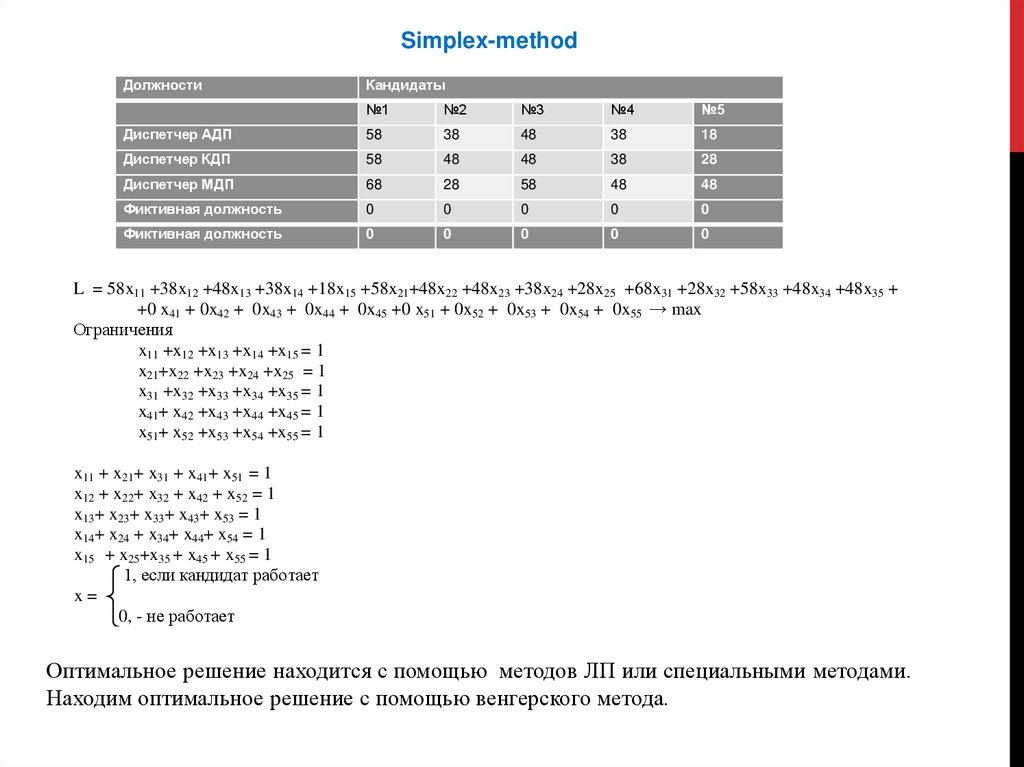
Simplex-method
Должности
Кандидаты
№1
№2
№3
№4
№5
Диспетчер АДП
58
38
48
38
18
Диспетчер КДП
58
48
48
38
28
Диспетчер МДП
68
28
58
48
48
Фиктивная должность
0
0
0
0
0
Фиктивная должность
0
0
0
0
0
L = 58x11 +38x12 +48x13 +38x14 +18x15 +58x21+48x22 +48x23 +38x24 +28x25 +68x31 +28x32 +58x33 +48x34 +48x35 +
+0 x41 + 0x42 + 0x43 + 0x44 + 0x45 +0 x51 + 0x52 + 0x53 + 0x54 + 0x55 → max
Ограничения
x11 +x12 +x13 +x14 +x15 = 1
x21+x22 +x23 +x24 +x25 = 1
x31 +x32 +x33 +x34 +x35 = 1
x41+ x42 +x43 +x44 +x45 = 1
x51+ x52 +x53 +x54 +x55 = 1
x11 + x21+ x31 + x41+ x51 = 1
x12 + x22+ x32 + x42 + x52 = 1
x13+ x23+ x33+ x43+ x53 = 1
x14+ x24 + x34+ x44+ x54 = 1
x15 + x25+x35 + x45 + x55 = 1
1, если кандидат работает
x=
0, - не работает
Оптимальное решение находится с помощью методов ЛП или специальными методами.
Находим оптимальное решение с помощью венгерского метода.

31.

Решение с помощью венгерского метода
Должности
Диспетчер АДП
Диспетчер КДП
Диспетчер МДП
Фиктивная должность
Фиктивная должность
Max
Кандидаты
№1
№2
58
38
58
48
68
28
0
0
0
0
68
48
Должности
Диспетчер АДП
Диспетчер КДП
Диспетчер МДП
Фиктивная должность
Фиктивная должность
№3
48
48
58
0
0
58
Кандидаты
№1
10
10
0*
68
68
Должности
Диспетчер АДП
Диспетчер КДП
Диспетчер МДП
Фиктивная должность
Фиктивная должность
№4
38
38
48
0
0
48
№5
18
28
48
0
0
48
Min
№2
10
0*
20
48
48
№3
10
10
0*
58
58
Кандидаты
№1
0*
10
0
20
20
№4
10
10
0
48
48
№2
0
0*
20
0
0
№5
30
20
0
48
48
№3
0
10
0*
10
10
10
0
0
48
48
№4
0
10
0
0*
0
№5
20
20
0
0
0*
В матрице назначений проводим минимальное число линий (горизонталей (по строкам) и/или вертикалей (по
столбцам)), вычеркивающих все нулевые ячейки матрицы. Если минимальное число вычеркнутых строк и
столбцов равно n (n=5), оптимальное решение найдено:
• диспетчер АДП - №5;
• диспетчер КДП - №1;
• диспетчер МДП - №2.
Остальные кандидаты (№3, №4) не прошли конкурсный отбор и остаются на подмене или в качестве резерва.
При этом можно определить условную максимальную производительность труда для оптимального выбора, для
нашего примера она составляет :
С = 58+48+58=164 у.е.

32.

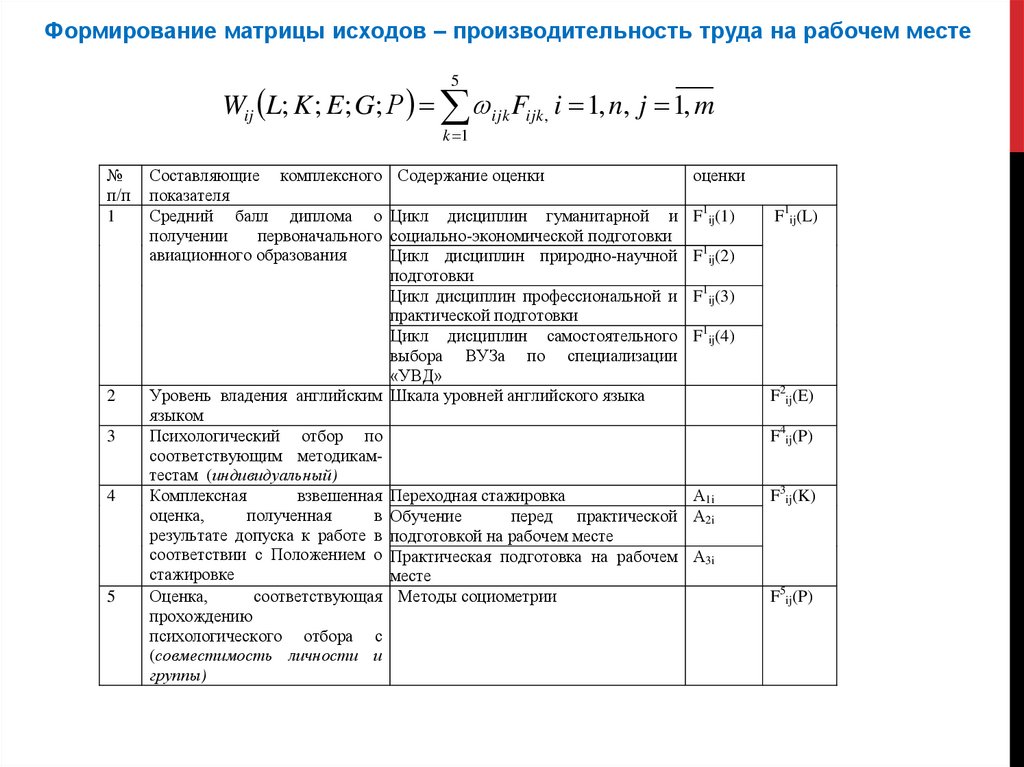
Формирование матрицы исходов – производительность труда на рабочем месте
5
Wij L; K ; E; G; Р ijk Fijk, i 1, n, j 1, m
k 1
№
п/п
1
2
3
4
5
Составляющие комплексного
показателя
Средний балл диплома о
получении
первоначального
авиационного образования
Содержание оценки
Цикл дисциплин гуманитарной и
социально-экономической подготовки
Цикл дисциплин природно-научной
подготовки
Цикл дисциплин профессиональной и
практической подготовки
Цикл дисциплин самостоятельного
выбора ВУЗа по специализации
«УВД»
Уровень владения английским Шкала уровней английского языка
языком
Психологический отбор по
соответствующим методикамтестам (индивидуальный)
Комплексная
взвешенная Переходная стажировка
оценка,
полученная
в Обучение
перед практической
результате допуска к работе в подготовкой на рабочем месте
соответствии с Положением о Практическая подготовка на рабочем
стажировке
месте
Оценка,
соответствующая Методы социометрии
прохождению
психологического отбора с
(совместимость личности и
группы)
оценки
F1ij(1)
F1ij(L)
F1ij(2)
F1ij(3)
F1ij(4)
F2ij(E)
F4ij(P)
А1i
А2i
F3ij(K)
А3i
F5ij(P)

33. Thank you for your attention

THANK YOU FOR
YOUR ATTENTION