График линейного уравнения с двумя переменными

1. График линейного уравнения с двумя переменными

2.

Функция -это зависимость одной переменной от
другой.
S(t); y(x);
График функции -это множество всех точек
координатной плоскости, абсциссы которых равны
значениям независимой переменной, а ординаты –
соответствующим значениям функции.
Функция y=kx – прямая пропорциональная
зависимость y(x).
k - коэффициент пропорциональности
Функция y=kx +b – линейная функция.

3.

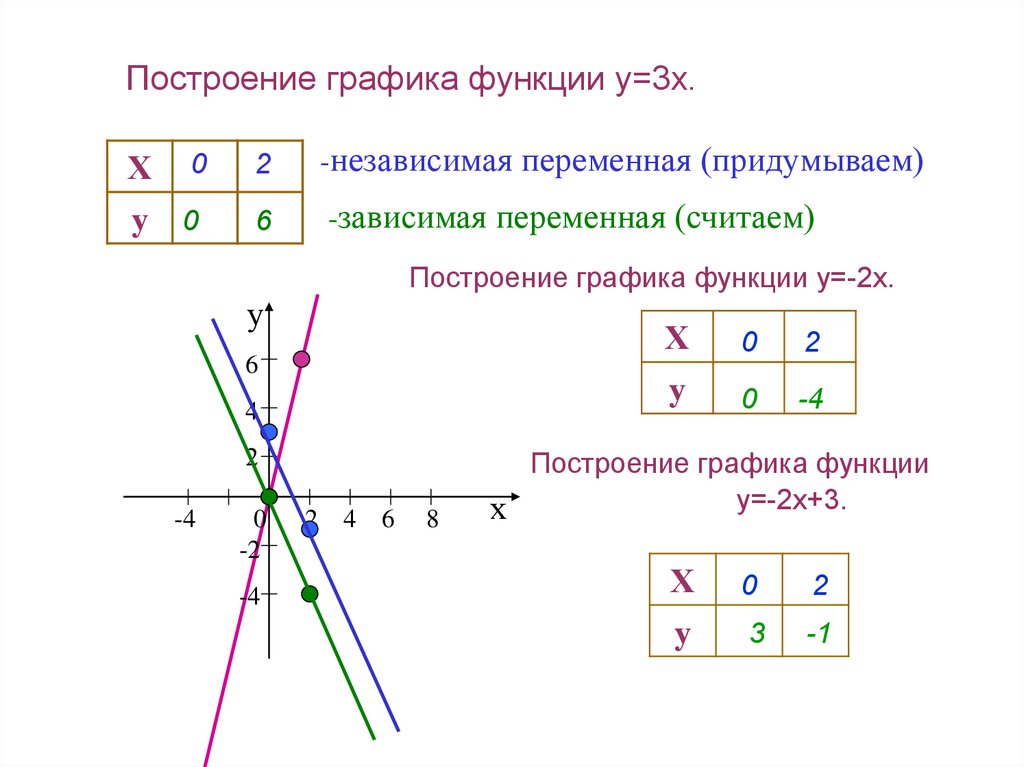
Построение графика функции y=3x.
Х 0
у 0
2
-независимая переменная (придумываем)
6
-зависимая переменная (считаем)
Построение графика функции y=-2x.
у
Х
у
6
4
2
-4
0
-2
-4
2 4
6
8
0
2
0
-4
Построение графика функции
y=-2x+3.
х
Х
0
2
у
3
-1

4.

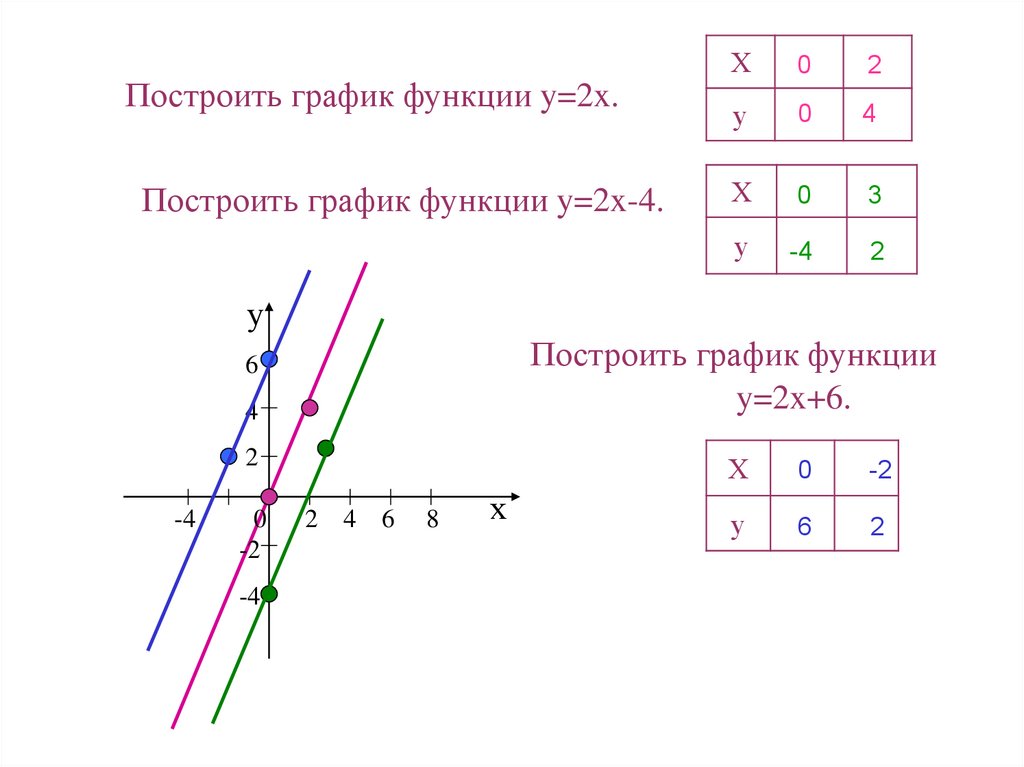
Построить график функции y=2x.
Построить график функции y=2x-4.
Х
0
2
у
0
4
Х
0
3
у
-4
2
у
Построить график функции
y=2x+6.
6
4
2
-4
0
-2
-4
2 4
6
8
х
Х
0
-2
у
6
2

5.

y
а
-8
б
8
в
6
е
ж
з
и
у
ф
х
ц
й
-6
э
-4
н
ю
-2
о
я
0
4
2
-2
г
д
к
л
м
ч
ш
щ
п
2
т
р
4
й
с
6
8
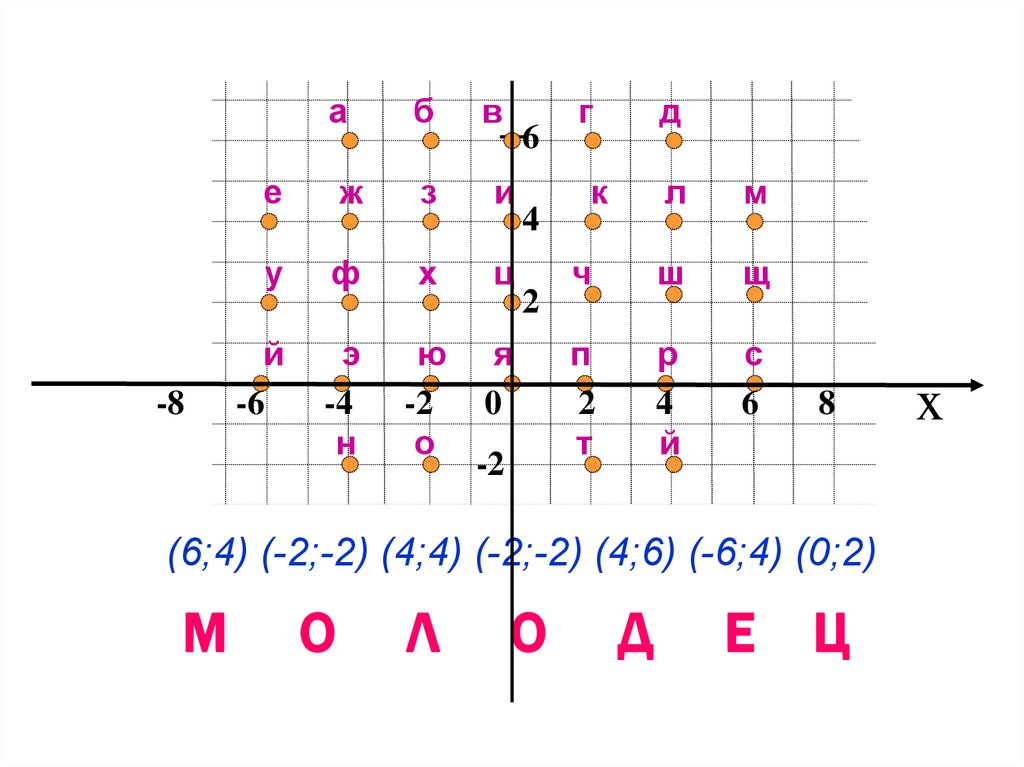
(6;4) (-2;-2) (4;4) (-2;-2) (4;6) (-6;4) (0;2)
М
О
Л
О
Д
Е
Ц
x

6. Выясним, что представляет собой график уравнения 3х+2у=6

Выразим переменную у через х
у=-1,5х+3
Формулой у=-1,5х+3 задается линейная
функция, графиком которой служит прямая.
Уравнения 3х+2у=6 и у=-1,5х+3
равносильны, то эта прямая является и
графиком уравнения 3х+2у=6

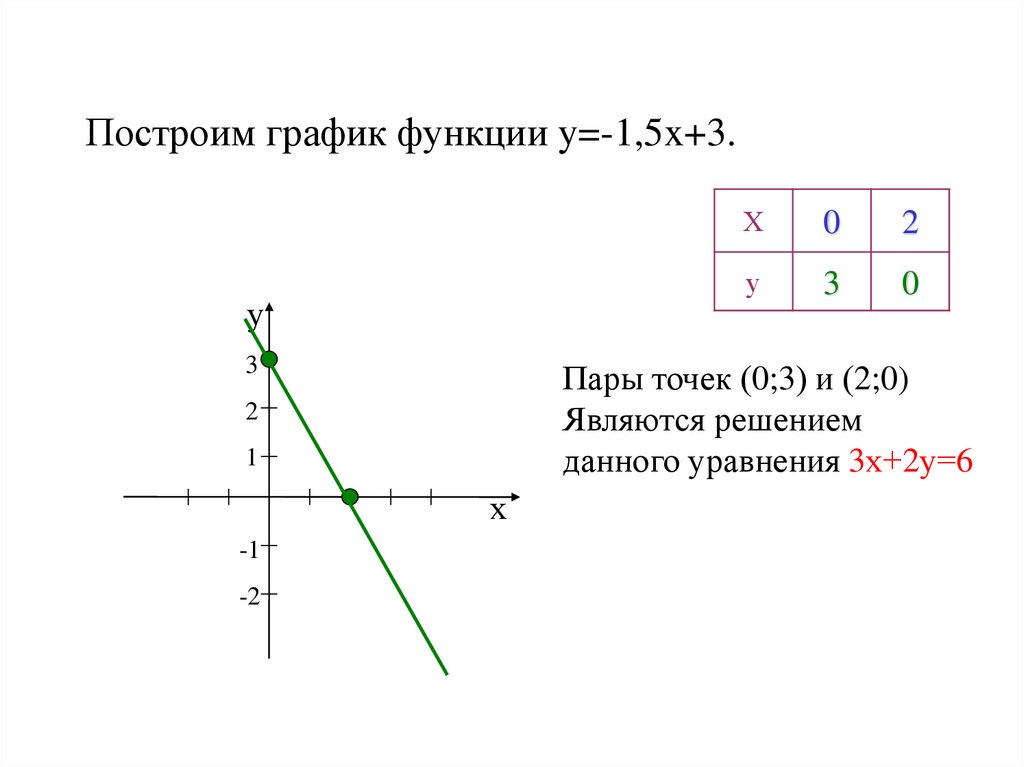
7. Построим график функции y=-1,5x+3.

у
3
1
х
-2
0
2
у
3
0
Пары точек (0;3) и (2;0)
Являются решением
данного уравнения 3х+2у=6
2
-1
Х

8. Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются

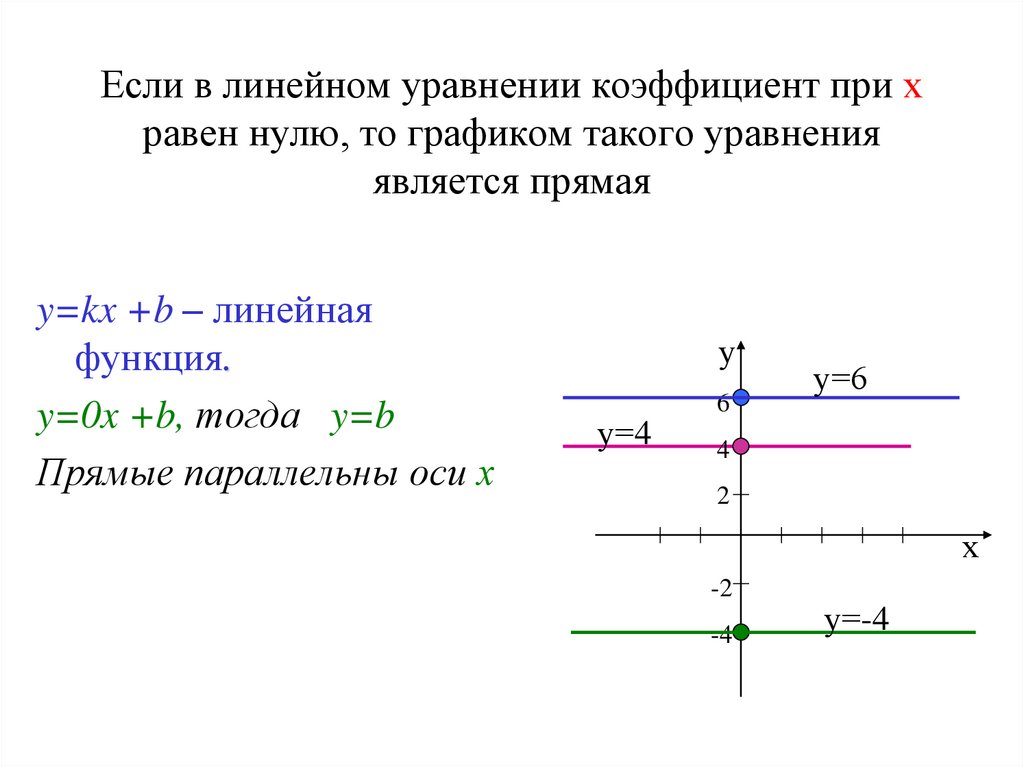
решениями этого уравнения

9. Если в линейном уравнении коэффициент при х равен нулю, то графиком такого уравнения является прямая

y=kx +b – линейная
функция.
y=0x +b, тогда y=b
Прямые параллельны оси х
у
у=4
6
у=6
4
2
х
-2
-4
у=-4

10. Если в линейном уравнении коэффициент при у равен нулю, то графиком такого уравнения является прямая

y=kx +b – линейная функция.
0y+kx=b, тогда х=b/ k
Прямые параллельны оси у
у
6
х=2
4
х=-4
2
-2
-4
х=4

11. Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентом при переменных не равен нулю,

является
прямая

12.

Уравнение ax+by=c, в котором оба
коэффициента при переменных равны
нулю, имеет вид 0x+0y=c. При с=0 любая
пара чисел является решением этого
уравнения,
а
его
графиком
-вся
координатная плоскость.
При с≠0 уравнение не имеет решений и его
график не содержит ни одной точки