Решение систем неравенств

1.

Решение систем
неравенств
Методическая разработка учителя математики
ГБОУ СОШ № 322 Дубровской Т.И.
Санкт- Петербург
2012 г.

2.

«Математика – наука о порядке»
А. Уайтхед.

3.

Алгоритм решения систем неравенств
Чтобы решить систему неравенств, надо:
1) решить каждое неравенство системы;
2) изобразить решение каждого неравенства данной системы
на одной числовой прямой.
3) записать решение системы, используя скобки, в случаях,
когда решением является отрезок, луч, интервал или
полуинтервал (решение может быть записано с помощью
простейшего неравенства)
4) записать ответ

4.

Блиц - опрос
Найти все решения системы неравенств и записать
ответ с помощью числового промежутка:
Ответ: полуинтервал [- 3,7; 5,1)
х 5,1,
1)
х 3,7;
х 7,9,
2)
х 3;
х 2,7,
3)
х 3,5;
х 3,
4)
х 1.
х 7,
5)
х 3,1.
Ответ: полуинтервал (3; 7,9]
Ответ: отрезок [-3,5; 2,7]
Ответ:
луч (3; + ∞)
Ответ: луч (- ∞;- 3,1]

5.

3 2 х 0,
Решить систему неравенств:
4 х 8 0.
Решение. 1) решим каждое неравенство исходной системы,
получим:
2 х 3 : (−2),
4 х 8 : 4;
х 1,5,
х 2.
2) изобразим решение каждого из
одной
получившихся неравенств на ____________
числовой прямой:

6.

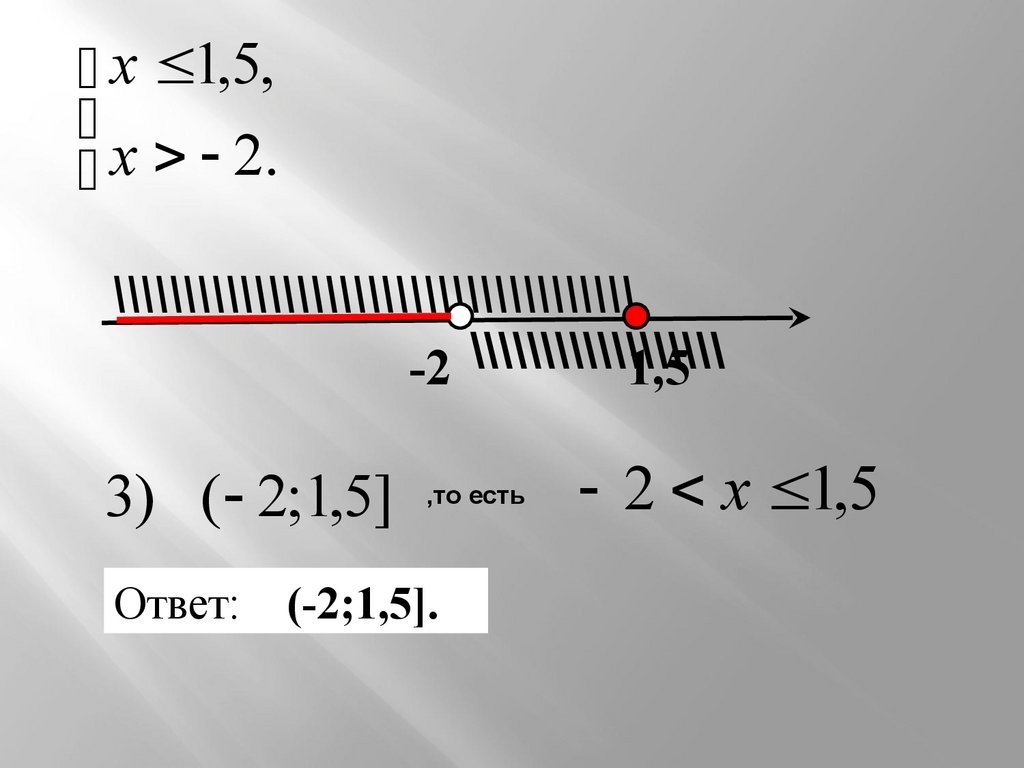
x 1,5,
x 2.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
-2 \\\\\\\\\\\\\\\\\\
1,5
3) ( 2;1,5]
Ответ:
,то есть
(-2;1,5].
2 х 1,5

7.

3 х 2 x 2,
Решить систему неравенств: х 15 6 2 x,
5 x 11 x 23.
Решение. 1) Решим каждое из неравенств данной системы
одновременно, получим:
3 х х 2 2,
х 2 х 6 15,
5 x х 23 11;
2х 4
3х 9
4 х 12
: 2,
: 3,
: 4;
х 2,
х 3,
х 3.
2) Изобразим решение каждого из
получившихся неравенств на одной числовой
прямой:

8.

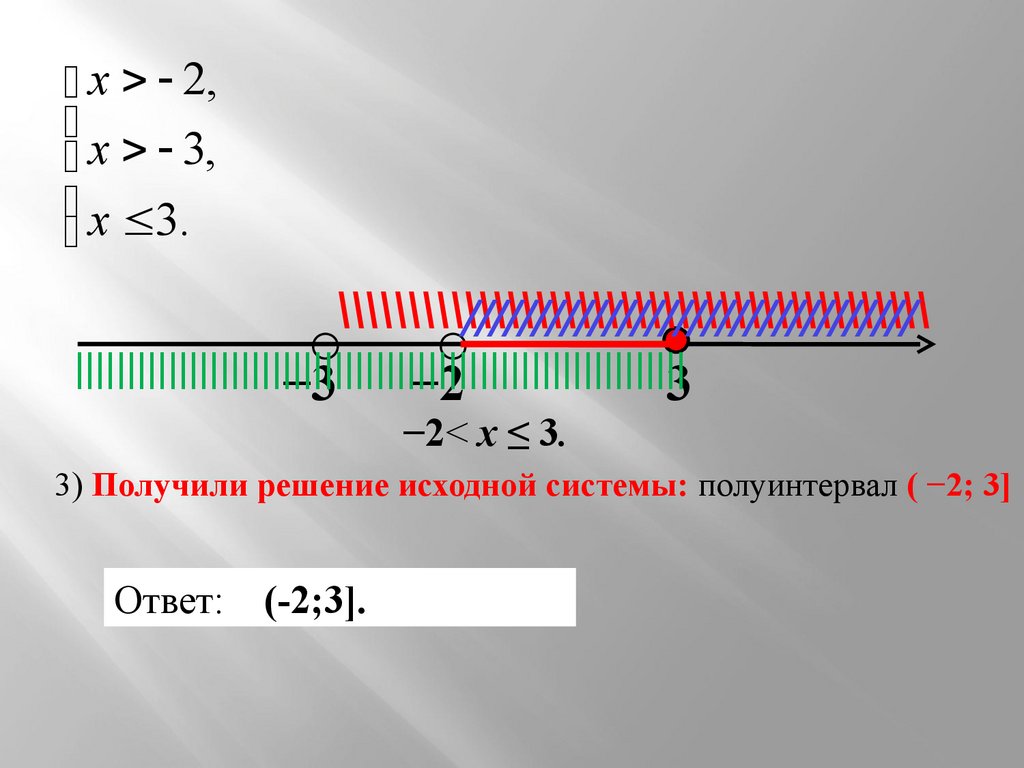
х 2,
х 3,
х 3.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
////////////////////////////////
○ ○
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
−3 −2
3
−2< х ≤ 3.
3) Получили решение исходной системы: полуинтервал ( −2; 3]
Ответ: (-2;3].

9.

Решить систему неравенств:
5( х 1) 3( х 3) 1,
2 х 1 х 1
7 2 .
Решение. 1) Решим каждое неравенство данной системы:
5 х 5 3х 9 1,
2(2 х 1) 7( х 1);
2 х 5
3 х 9
: 2,
: (−3);
5 х 3х 10 5,
4 х 2 7 х 7;
х 2,5,
х 3.

10.

2) Изобразим решение каждого из
получившихся неравенств на одной числовой
прямой:
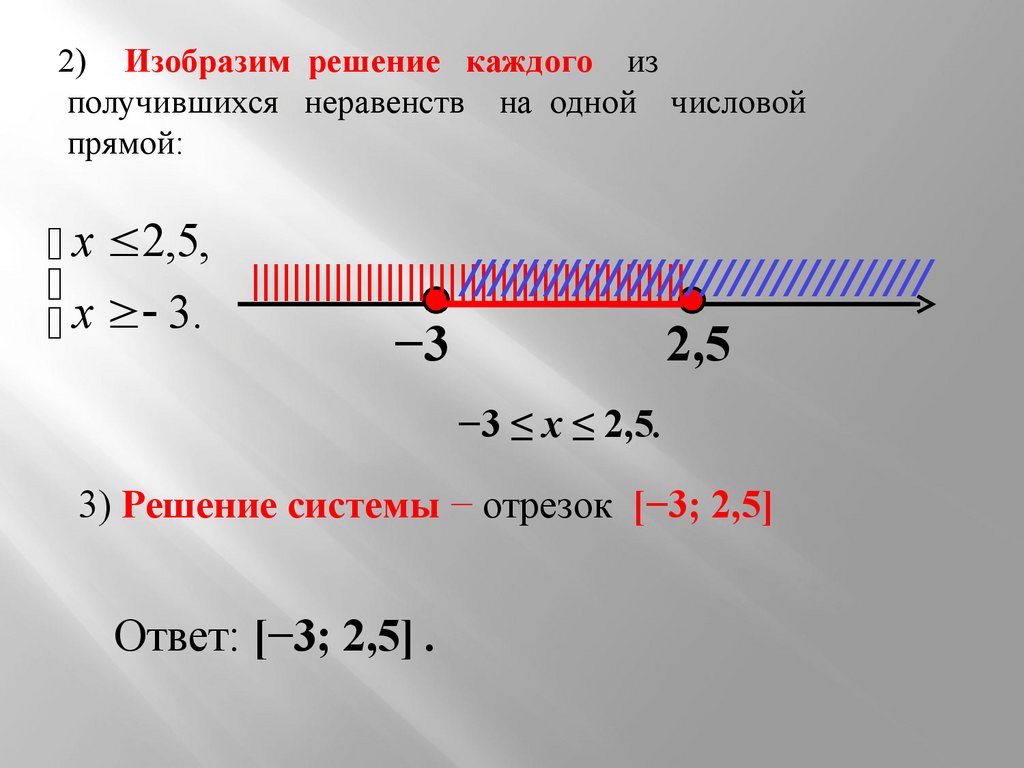
х 2,5,
||||||||||||||||||||||||||||||||||||||||||
/////////////////////////////////
х 3.
−3
2,5
−3 ≤ х ≤ 2,5.
3) Решение системы − отрезок [−3; 2,5]
Ответ: [−3; 2,5] .

11.

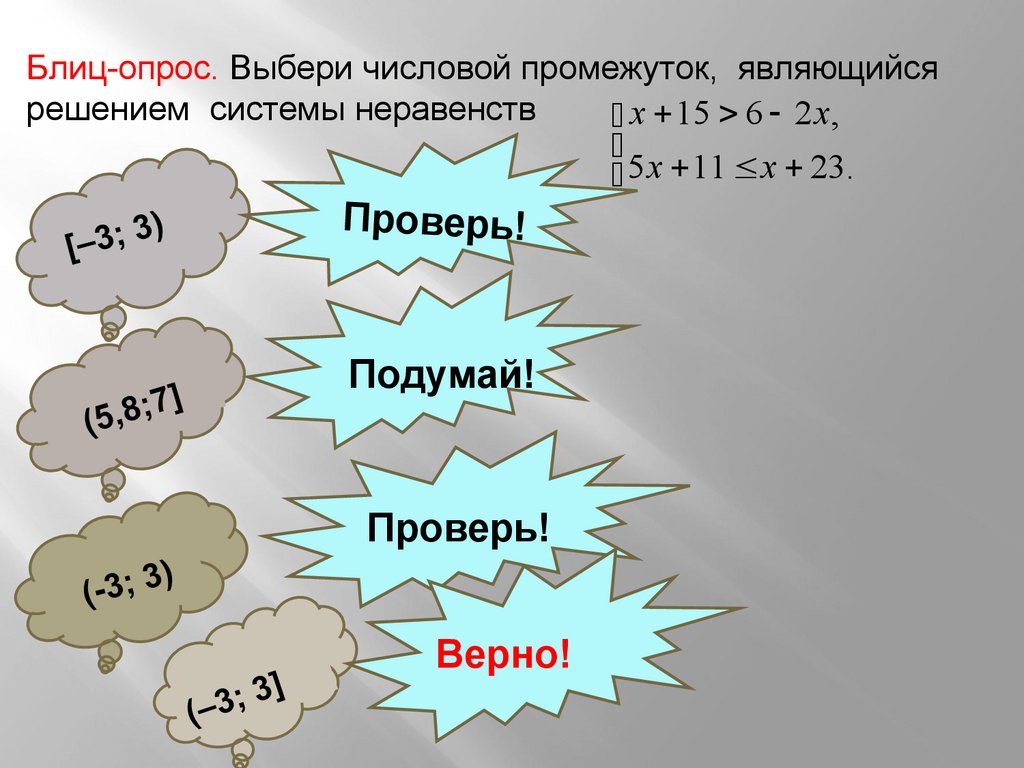
Блиц-опрос. Выбери числовой промежуток, являющийся
решением системы неравенств
х 15 6 2 x,
5 x 11 x 23.
Проверь!
Подумай!
Проверь!
Верно!

12.

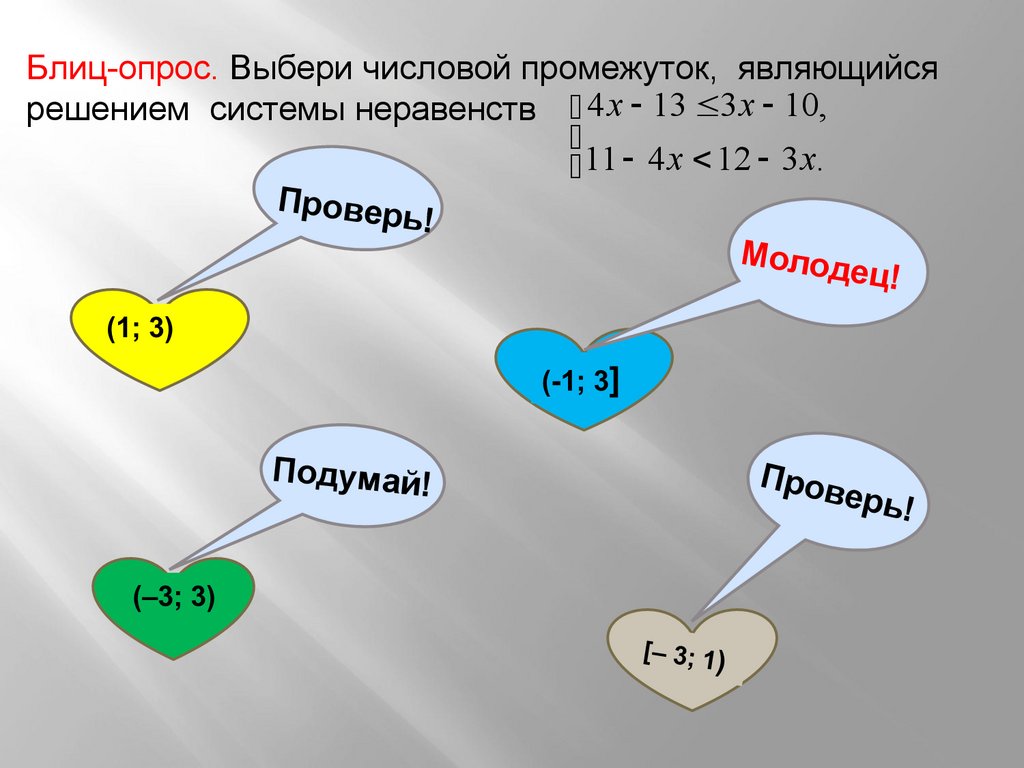
Блиц-опрос. Выбери числовой промежуток, являющийся
решением системы неравенств 4 х 13 3x 10,
11 4 x 12 3x.
Провер
ь!
Молод
ец!
Подумай!
Пров
ерь!

13.

Блиц-опрос. Выбери наибольшее целое решение системы
3( х 8) 4(7 x),
( x 2)( x 5) ( x 3)( x 4).
Думай!
0
Молодец!
Думай!
1
Думай!
-1
Нет
такого

14.

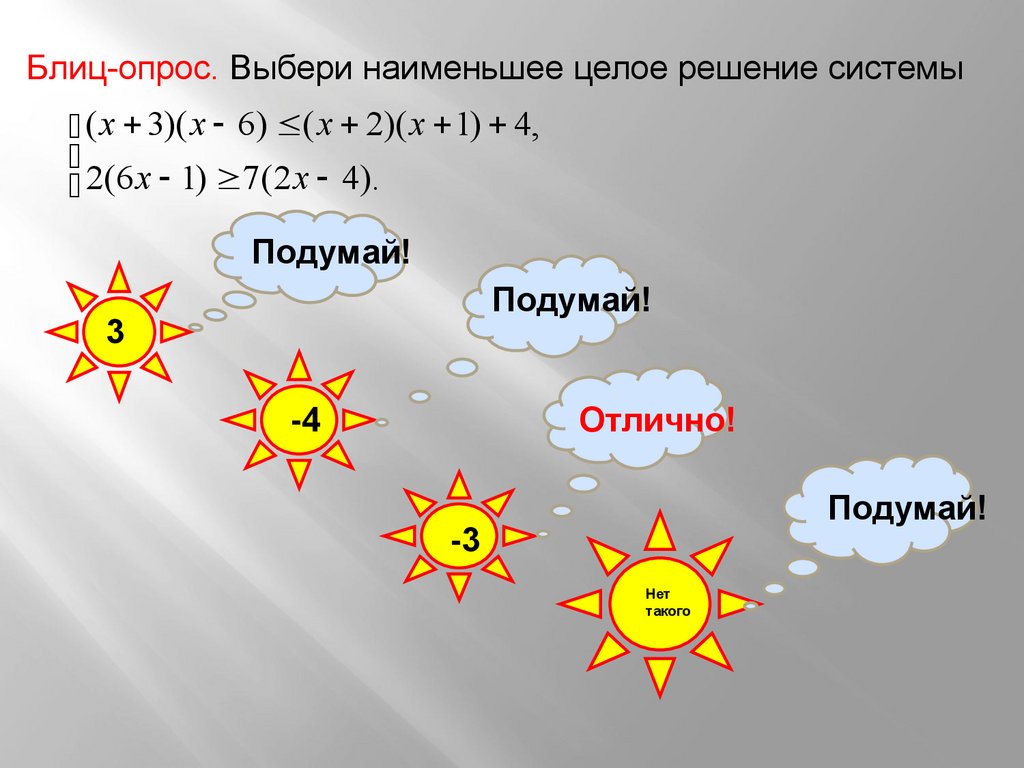
Блиц-опрос. Выбери наименьшее целое решение системы
( х 3)( х 6) ( x 2)( x 1) 4,
2(6 x 1) 7(2 х 4).
Подумай!
Подумай!
3
-4
Отлично!
Подумай!
-3
Нет
такого

15.

Задача. Одна сторона треугольника равна 5 метрам, а другая- 8
метрам. Какой может быть третья сторона, если периметр
треугольника больше 17 метров ?
Решение. Пусть x метров (x>0) — длина третьей стороны
треугольника, тогда, согласно условию задачи и учитывая
неравенство треугольника, составим и решим систему неравенств:
13 х 17
х 13
х 5 8,
5 8 х 17.
х 17 13
х 13
х 4
х 13
/
///////////////////////////////////////////////
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
4
13
4< х < 13, значит, длина третьей стороны есть любое число из
интервала 4< х < 13.
Ответ: длина третьей стороны больше 4 метров, но меньше 13 метров.