Разработка и реализация алгоритма создания и балансировки двоичного дерева поиска со взвешенными узлами

1.

Разработка и реализация алгоритма
создания и балансировки двоичного дерева
поиска со взвешенными узлами
Подготовила Колосова Ирина, гр. 4940

2.

Цель работы
Разработка структуры:
-минимальные затраты памяти;
-быстрый поиск;
-приоритезированный доступ.
Реализация структуры.
Анализ эффективности.
Визуализация.

3.

Балансировка двоичных деревьев
поиска
По высоте
По весу
По количеству узлов

4.

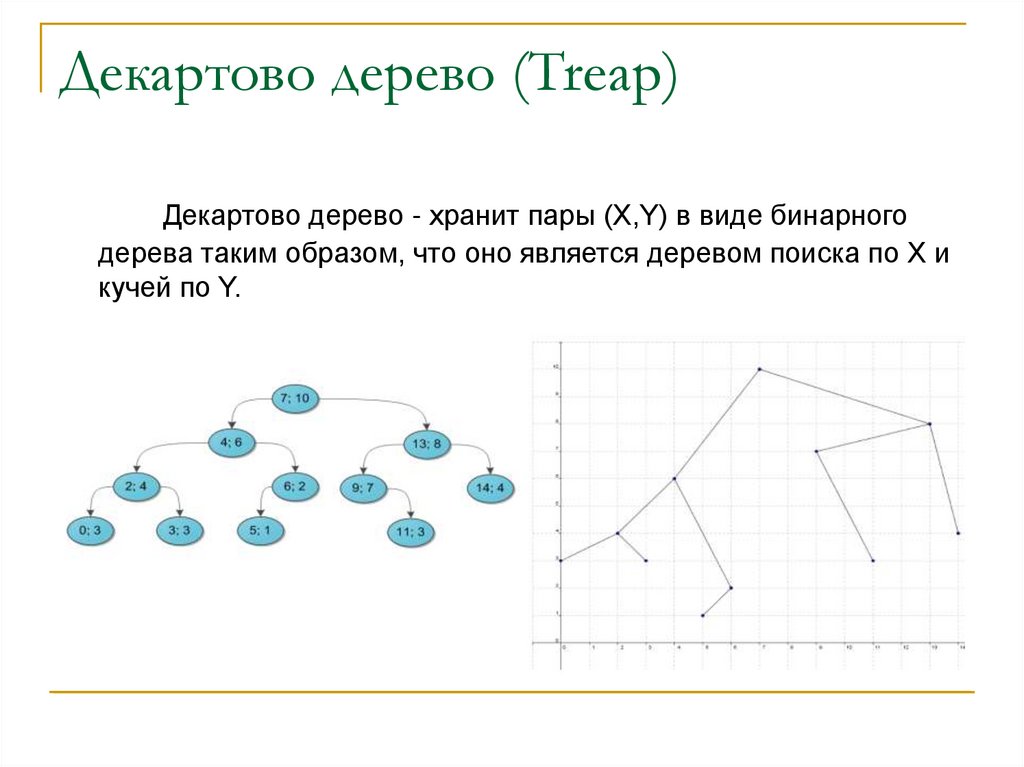
Декартово дерево (Treap)
Декартово дерево - хранит пары (X,Y) в виде бинарного
дерева таким образом, что оно является деревом поиска по X и
кучей по Y.

5.

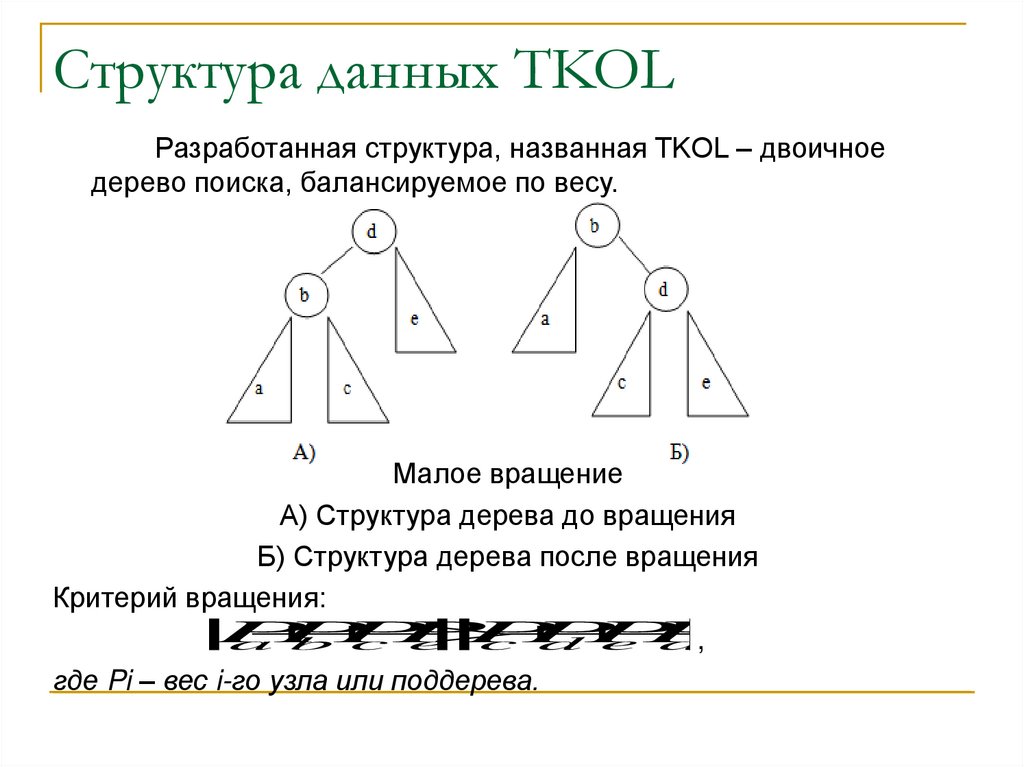
Структура данных TKOL
Разработанная структура, названная TKOL – двоичное
дерево поиска, балансируемое по весу.
Малое вращение
А) Структура дерева до вращения
Б) Структура дерева после вращения
Критерий вращения:
|
P
P
P
P
|
|
P
P
P
P
|,
a
b
c
e
c
d
e
a
где Pi – вес i-го узла или поддерева.

6.

Теоретический анализ
Количество переходов по дереву до случайного элемента
составляет
P
P
left
left
,
T
(
N
,
P
)
T
(
N
,
P
)
(
1
T
(
N
N
1
,
P
)
left left
left)
left
left
P
P
где:
Pleft - вес левого поддерева;
P - вес всего дерева;
N left - количество узлов в левом поддереве;
N - суммарное количество узлов дерева.

7.

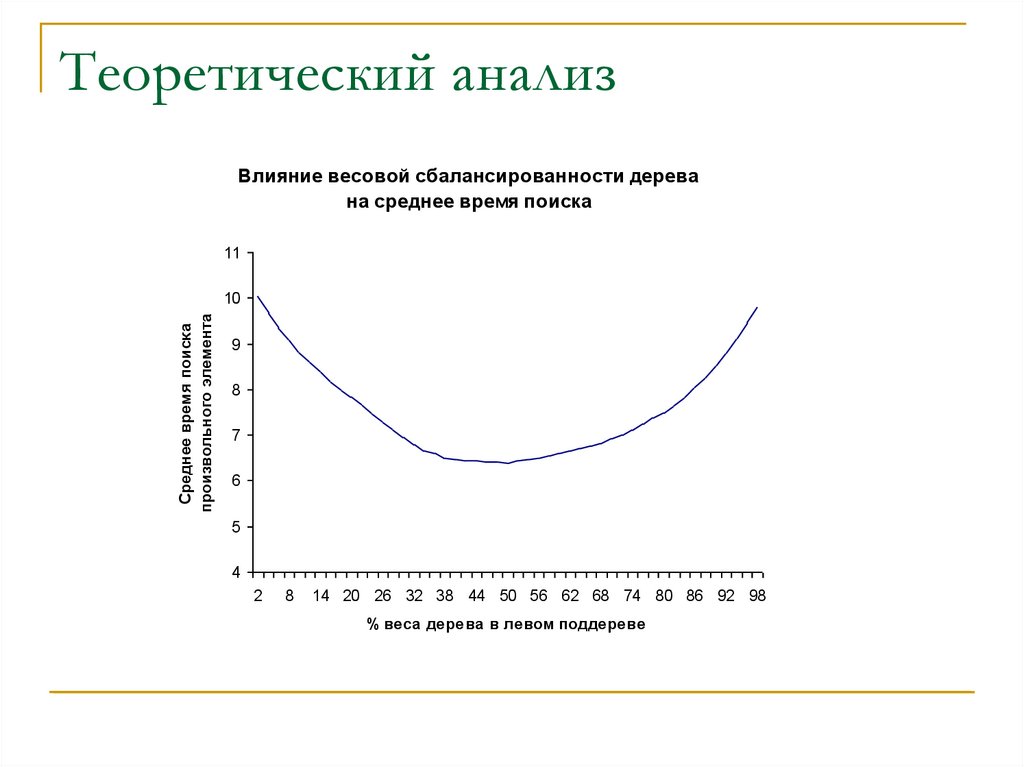
Теоретический анализ
Влияние весовой сбалансированности дерева
на среднее время поиска
11
Среднее время поиска
произвольного элемента
10
9
8
7
6
5
4
2
8
14 20 26 32 38 44 50 56 62 68 74 80 86 92 98
% веса дерева в левом поддереве

8.

Средневзвешенный путь
P d
AWD
P
i
,
i
где Pi — собственный вес узла;
d — длина пути от корня до узла,
увеличенная на единицу.

9.

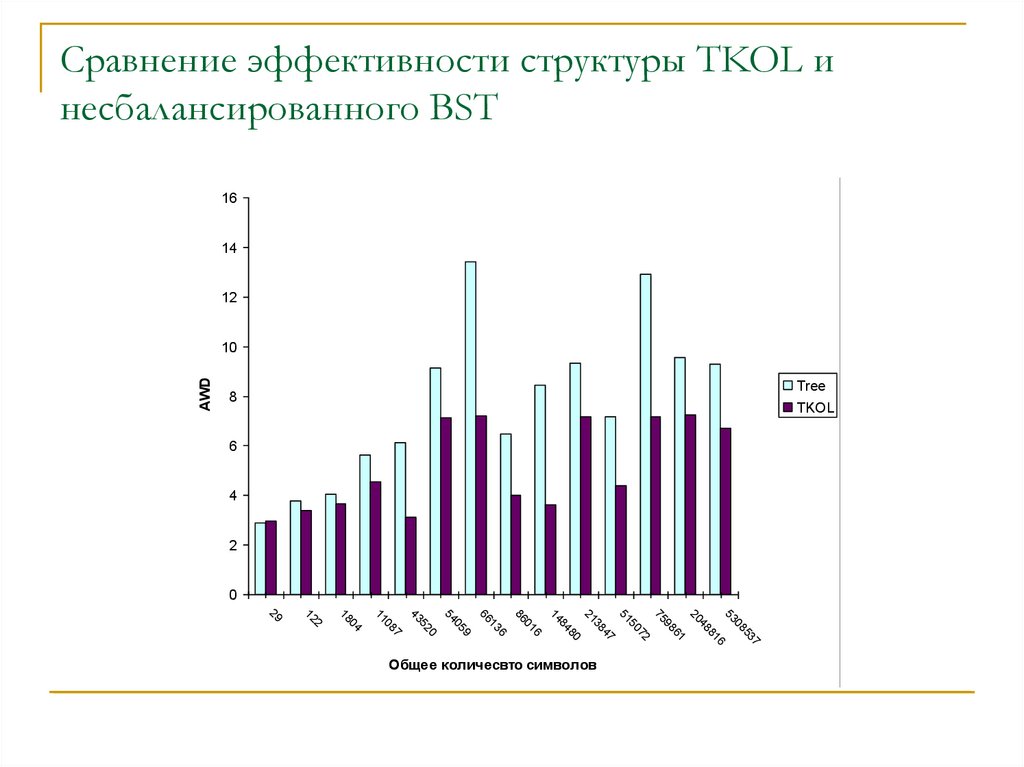
Сравнение эффективности структуры TKOL и
несбалансированного BST
16
14
12
AWD
10
Tree
8
TKOL
6
4
2
0
08
53
48
20
98
75
50
51
38
21
84
14
01
86
13
66
05
54
52
43
08
11
04
18
2
12
29
7
53
6
81
61
72
47
80
6
6
9
0
7
Общее количесвто символов

10.

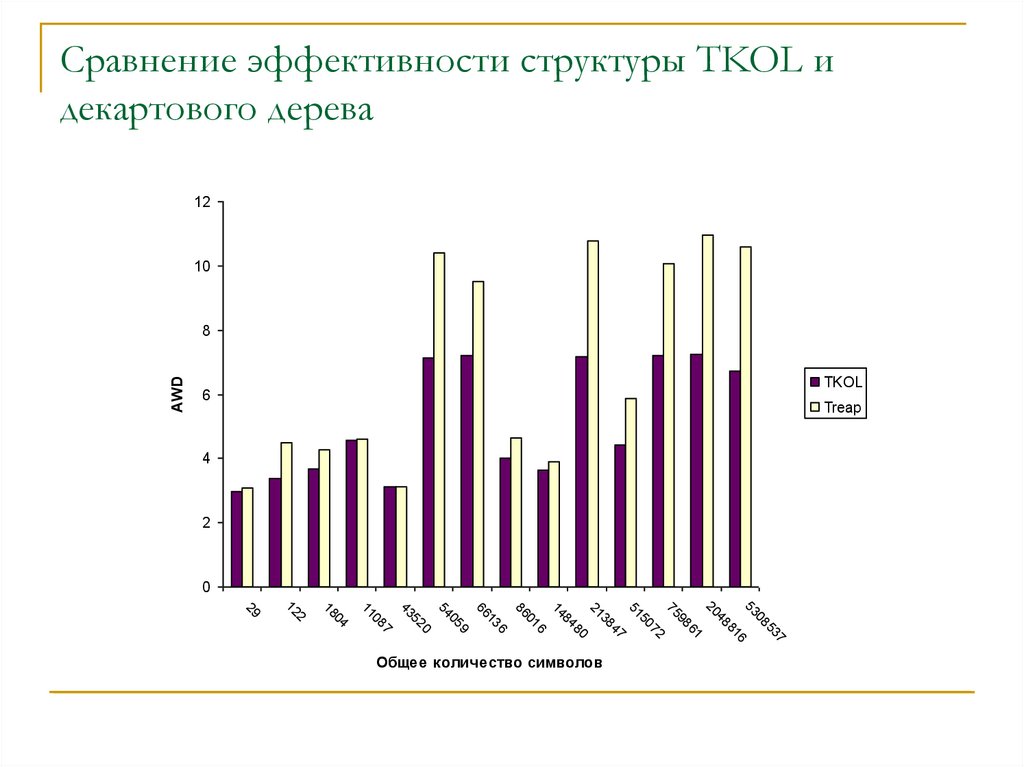
Сравнение эффективности структуры TKOL и
декартового дерева
12
10
AWD
8
TKOL
6
Treap
4
2
0
7
53
08
53
6
81
48
20
61
98
75
72
50
51
47
38
21
80
84
14
6
01
86
6
13
66
9
05
54
0
52
43
7
08
11
04
18
2
12
29
Общее количество символов