Similar presentations:
Неравенства. Задачи на повторение
1. Задачи на повторение класс
2.
№1 Какое из чисел является рациональным?9
1) 900 2)
10
3) 9000 4)ни одно из этих чисел
Ответ: 1)
№2
Тираж газеты «Аргументы и факты» составляет
около 2 млн 990 тыс. экземпляров. Как эта
величина записывается в стандартном виде?
1) 2,99 10
Ответ: 2)
4
2) 2,99 10
6
3) 2,99 10 4) 2,99 10
7
5
3.
№3 Какое из следующих неравенств нельзяполучить из неравенства b< a+c ?
1) b-c<a 2) a>b-c 3)a-b+c>0 4) b-a-c>0
Ответ: 4)
№4
Расположите в порядке убывания следующие
числа: 0,0802; 0,08; 0,208.
Ответ: 0,208; 0,0802; 0,08.
4.
№7Решите неравенство
3x 5 4 x 3
3
.
2 8
6
1
Ответ: ( ; 2 )
4
№8 Найдите все значения переменной a, при
каждом из которых значение выражения
a
a 14
a( 5)
4a неотрицательно
3
3
2
2
Ответ: при а ( ; 4
3
5.
№9 Укажите промежуток, являющийся решениемсистемы неравенств
x ≥ a,
x ≤ b при условии, что a<b.
Ответ: a; b
№10 Решите систему неравенств
3x 5 4 x 3
3
,
2 8
6
1
7
3
5( x 3) 3 x.
2
4
2
Ответ: ( ; 2,25)
6.
№11 Отметьте на координатной прямойрешение совокупности неравенств
x a,
x b при условии, что а<b.
Ответ: ( ; a) (b; )
№12 При каких значениях x значения выражения
4-x принадлежат отрезку [0;2]? Ответ: [2;4]
№13 Решите неравенство |3x-1|≤ 4
2
Ответ: 1 ;1 3
№14 Решите неравенство |1-3x|≥ 4
Ответ:
2
; 1 1 ;
3
7.
№15Решите неравенство 3x2-5x-2 > 0
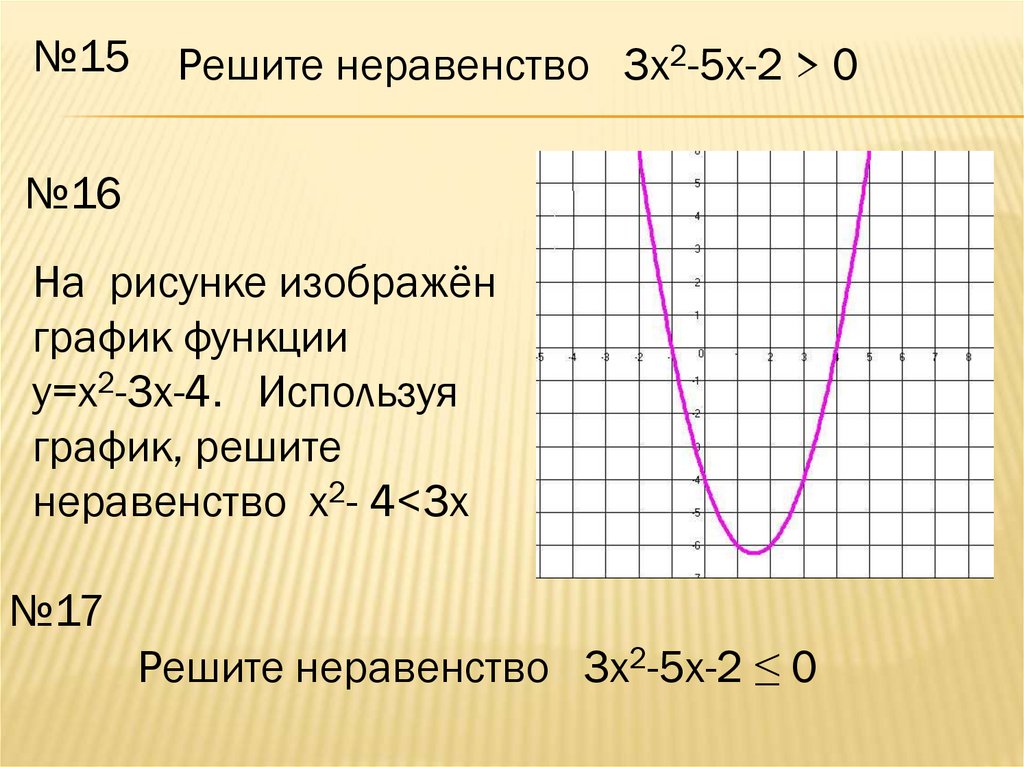
№16
На рисунке изображён
график функции
y=x2-3x-4. Используя
график, решите
неравенство x2- 4<3x
№17
Решите неравенство 3x2-5x-2 ≤ 0
8.
№18Выясните, имеет ли решения неравенство
X2+4x+2x√6+20 ≤ 0
№19
Решите неравенства:
А) x2-5x < 0
б) x2- 4 ≥ 0
в)
x2-
9≤0
с помощью схематичного
изображения параболы.
используя модуль.
Ответы: а) (0;5) б)(-∞;-2]υ[2;+∞)
в)[-3;3]
9.
№20 Решить неравенства:а) x2- 8x+15 ≥ 0
б) 8 - 2x2 > 0
в) (2+7x)2 ≤ (4 - 3x)2
Ответ: (-∞;3]υ[5;+∞)
Ответ: (-2; 2)
Ответ: [-1,5; 0;2]
№21 Найти область определения функции
x 1
y
6 x 2 11x 5
Ответ: xϵ (5/6; 1)
10.
№22Решить неравенства методом интервалов:
x2
x
а)
6 2x 3 x
б) x x
3
2( x 1)
в)
0
14 7 x
Ответ: (- ;0)υ(2;3)
Ответ: (-1;0)υ(1;+∞)
Ответ: (-1;2)
11. Уравнения с двумя переменными. Системы уравнений.
УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ.СИСТЕМЫ УРАВНЕНИЙ.
№100
Решите уравнение (x-4)2+(4y-12)2=0
№2 Постройте график уравнения
X2 –2x + y2 - 3=0
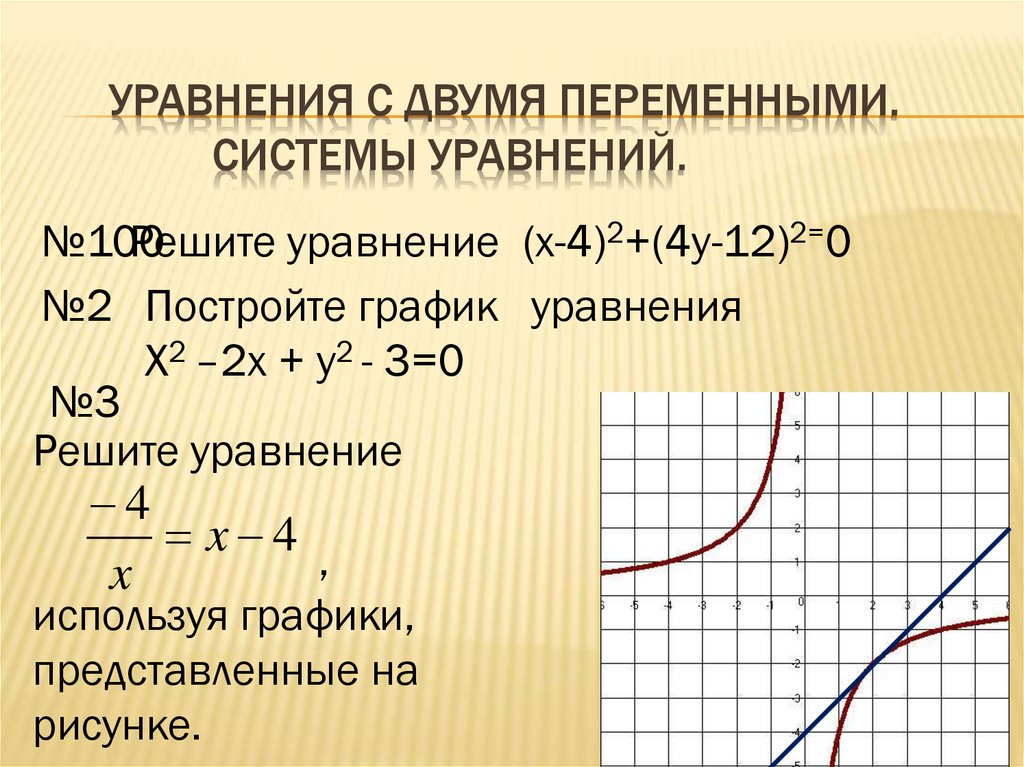
№3
Решите уравнение
4
x 4 ,
x
используя графики,
представленные на
рисунке.
12.
Способ подстановки№4 Решите систему уравнений
x 2 y 2 0,
xy 12.
№5 Докажите, что система уравнений
x y 6,
2
не имеет решений.
2
x y 9
(Графически и аналитически)
13. Способ сложения
СПОСОБ СЛОЖЕНИЯ№6
Решите систему уравнений
р 3xy 2 y 5,
x 3xy 2 y 3.
14. Способ введения новых переменных
СПОСОБ ВВЕДЕНИЯ НОВЫХ ПЕРЕМЕННЫХ№8 Решите систему уравнений
№9 Решите систему уравнений
( x 2) 2 (2 y 1) 10,
( x 2)( 2 y 1) 3.
3 1
4,
x 2y
6 1
5.
x 2y
15. Домашнее задание
ДОМАШНЕЕ ЗАДАНИЕ№1 Решите систему уравнений:
( x 2)( y 1) 12,
a)
x 2 y 6.
x 2 y 2 10,
б )
xy 3.
№9 Не выполняя построений, найдите
координаты точек пересечения параболы
2
2
2
y x 5 и окружности x y 25.
16. Решение задач по теме: «Арифметическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ»
№1 Дано : а1 1
d 3
Найти : а2 , а3 , а4 .
№2 Дано : а1 17
d 2
Ответ: 4,7,10.
Ответ: 5.
Найти : а7 .
№3 Дано : 1, 2, 3, ...118,119,120
арифметическая прогрессия
Найти : S120.
Ответ: 7260.
17. Решение задач по теме: «Арифметическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ»
№4 Дано : а1 4
d 5
Найти : S19 .
Ответ: 779.
№5 Дано : (аn ) арифметическая прогресия
а14 а16 36
Найти : а15 .
Ответ: 18.
№6 Определить, являются ли числа143, 155, 167 тремя
последовательными членами арифметической
прогрессии ?
18. Решение задач по теме: «Арифметическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ»
№7
Дано : а7 2
Найти : a6 a8 .
Ответ: -4.
№8 Дано : а1 , а2 , а3 ...а7 арифметическая прогресия
а3 а5 7
Найти : S 7 .
Ответ: 24,5.
19. Решение задач по теме: «геометрическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
№9 Какая из последовательностей чисел
1) 2; 6; 18; 54...
2) 3; 6;12; 24; 48...
3) 3; 6; 12; 24...
является геометрической прогрессией ?
№10Дано : (bn ), геометрическая прогресия
b1 2
q 4
Найти : b2 , b3 , b4 .
Ответ: -8,-32,-128..
20. Решение задач по теме: «геометрическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
№11
Дано : (bn ), геометрическая прогресия
b1 5
q 3
Найти : b5 .
Ответ: 405.
№12
Дано : (bn ), геометрическая прогресия
b1 7
q 2
Найти : b3 .
Ответ: 28.
21. Решение задач по теме: «геометрическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
№13
Дано : (bn ), геометрическая прогресия
b1 3
q 2
Найти : S 7 .
Ответ: 381.
№14
Дано : (bn ), геометрическая прогресия
b6 12 2
q 2
Найти : b5 b7 .
Ответ: 288.
22. Решение задач по теме: «геометрическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
№15
Определить, являются ли числа 1, 3 , 3 тремя
последовательными членами геометрической
прогрессии ?
№16
Дано : b1 , b2 ...b10 геометрическая прогресия
b1 b10 72
q 2
Найти : b4 b7 .
Ответ: 72.
23. Решение задач по теме: «геометрическая прогрессия»
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ:«ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ»
№17
Дано : b1 , b2 ...b10 геометрическая прогресия
b3 27
b2 b9 3
Найти : b8 .
Ответ: 5
.
24. Решение более сложных задач по теме: «Арифметическая и геометрическая прогрессии»
РЕШЕНИЕ БОЛЕЕ СЛОЖНЫХ ЗАДАЧ ПОТЕМЕ: «АРИФМЕТИЧЕСКАЯ И
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ»
№18
Последовательность задана формулой yn=3n-2.
Является ли эта последовательность
арифметической прогрессией?
Ответ:d=3
№19
Найдите три числа, которые следует поместить
между числами 5 и 13, чтобы они вместе с
данными образовали арифметическую
прогрессию.
Ответ:7,9, 11.
25.
№20Найдите двадцать первый член арифметической
прогрессии, если известно, что её десятый член
равен 16, а разность равна 2.
Ответ: 38
№21
Запишите формулу общего члена
арифметической прогрессии (аn), если а5=60,
а7=30.
Ответ: аn=135-15n
26.
№22Шестой член арифметической прогрессии в 6
раз больше её третьего члена, а при делении с
остатком седьмого члена на четвёртый в частном
получается 2 и в остатке - 7. Найдите
девятнадцатый член этой прогрессии.
Ответ: 83
№23
Найдите сумму первых 16 членов
арифметической прогрессии , если известны два
её первых члена а1=-3,2, и а2=1.
Ответ:452,8
27.
№24Найдите первый член и разность
арифметической прогрессии, если суммы первых
четырёх и первых шести членов соответственно
равны S4=9 и S6=22,5.
Ответ: a1=0; d=1,5
№25
Cумма всех восьми членов конечной
1
арифметической прогрессии равна 21 .
3
Найдите сумму третьего и шестого
членов этой прогрессии.
1
Ответ: 5
3
28.
№26При каких значениях x значения выражений 2x,
3x+2, 5x+1, взятые в указанном порядке,
образуют конечную арифметическую
прогрессию? .
Ответ: 3.
№27
Найдите три положительных числа, которые
1
следует поместить между числами 2 и 10 ,
8
Чтобы они вместе с данными образовали
геометрическую прогрессию.
1 3
Ответ: 3, 4 , 6
2
4
29.
№28Найдите сумму первых шести членов
геометрической прогрессии (bn), если b4=3√3,
b7=27.
Ответ: 13(√3+1).
№29
При каких значениях х значения выражений x,
2x, x+2, взятые в указанном порядке образуют
конечную геометрическую прогрессию?
2
Ответ:
3
30.
№30Найдите произведение первых семи членов
геометрической прогрессии
2
,… .
2 , 1,
2
1
Ответ:
128
31. Решение текстовых задач
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ№1 (Задача на работу)
Две бригады по плану должны были, работая
вместе, отремонтировать повреждённый
участок шоссе за 18 дней. В действительности
сначала работала только первая бригада, а
затем – только вторая бригада,
производительность труда которой была более
высокой, чем у первой бригады. В результате
ремонт повреждённого участка занял 40 дней,
причём первая бригада выполнила 2/3 всей
работы. За сколько дней одна первая бригада
смогла бы отремонтировать повреждённый
участок шоссе?
Ответ: 45
32.
№2 (Задача на движение)Из пункта В в пункт А вышел пешеход. Через 6
часов из пункта А в пункт В навстречу первому
вышел второй пешеход. При встрече
выяснилось, что второй пешеход прошёл на 12
км меньше первого. Отдохнув, они
одновременно продолжили путь, каждый в
своём направлении с прежней скоростью. В
результате второй пешеход пришёл в пункт В
через 8 часов, а первый – в пункт А через 9
часов после встречи. Найдите расстояние
между пунктами А и В.
Ответ: 84 км
33. Функция, область определения, область значений функции.
ФУНКЦИЯ, ОБЛАСТЬ ОПРЕДЕЛЕНИЯ,ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ.
x
№1 Дана функция y 2
. Найдите
x 1
значения этой функции при x=0, X=1, X=-2.
Ответ: 0; 0,5; -0,4.
№2
Длина одной из сторон прямоугольника равна k.
Выразите формулой зависимость между длиной
второй стороны прямоугольника и его
площадью.
Ответ: S=kx.
34.
№3Функция задана формулой y 2 x ax 5.
Найдите значение параметра a, если y ( 5 ) 0 .
2
№4
Ответ: √5
Найдите область определения функции
f ( x) 16 x .
2
Ответ: [-4;4]
№5 Найдите наименьшее целое число,
принадлежащее области определения
функции
x 9
f ( x)
x 1
Ответ: -9
35.
№6 Найдите сумму целых чисел, входящих вобласть определения функции
1
y
.
Ответ: 15.
5x x 2 6
№7 Найдите область значений функции
y ( x 2)(1 x)
Ответ: (-∞; 0,25].
№8 Найдите область значений функции
1
y 2 .
x 1
Ответ: (0;1].
36.
№9 Какие из указанных функций являютсячётными, а какие – нечётными?
x
x 1
2
4
1) y 1 x x , 2) y 2 , 3) y 2 .
x 1
x 1
№10 Найдите все значения аргумента,при
которых функция y=-2x+8
принимает положительные значения.
Ответ: (-∞; 4).
№11 Найдите все значения аргумента, при
которых функция
x 1
y
x 2
принимает отрицательные значения.
Ответ: (-1;2).
37.
№12 Найдите наименьшее значение функции2
x 1
f ( x) 2
Ответ: 0,5.
x 2
№13 Найдите линейную функцию, график
которой проходит через точки с
координатами (2;3) и (0;1)
Ответ: y=x+1.
№14
Найдите уравнение прямой, параллельной
прямой y=2x+1 и проходящей через точку
с координатами (2;3).
Ответ: y=2x-1.
38.
№15 Найдите абсциссы точек пересеченияграфика функции y x 2 3x 2
с осью абсцисс.
Ответ: 1; 2.
№16 Укажите число общих точек графика
2
y
3
x
2 x 5 и оси абсцисс
функции
Ответ: 2.
№17
Найдите все значения x, при которых функция
2
y 3x 5 x 2 принимает отрицательные
значения
1
Ответ: ; 2; .
3





































 mathematics
mathematics








