Квадратичная функция

1.

8 класс
Учитель математики
Герасимова Т.Н.
ГОУ СОШ № 294
г.Санкт-Петербург

2.

График функции
У = f (x)
Графиком функции называется множество точек
координатной плоскости, абсциссы которых равны
значениям аргумента, а ординаты соответствующим
значениям функции.
Теория
Практикум
Тренажер
Алгоритм построения графика
Дополнительные задания

3.

Определение квадратичной функции
Функция у
= ах² + bx + c , где а, b и с заданные
числа, а≠0, х – действительная переменная,
называется квадратичной функцией.
Примеры:
у = -5х² + 3х – 6;
а = -5, b = 3; с = -6
у = 0,2х² -7х + 8;
а = 0,2, b = -7, с = 8

4. Теория

Вид функции
у х
2
у aх 2
у ах 2 n
у a( х m) 2
у aх bx c
2
Координаты
вершины параболы
График
функции
парабола
(0;0)
(0;0)
(0;n)
(m;0)
( x0 ; y0 )
b
x0
2a
парабола
парабола
парабола
y0 y ( x0 )
парабола
домой

5.

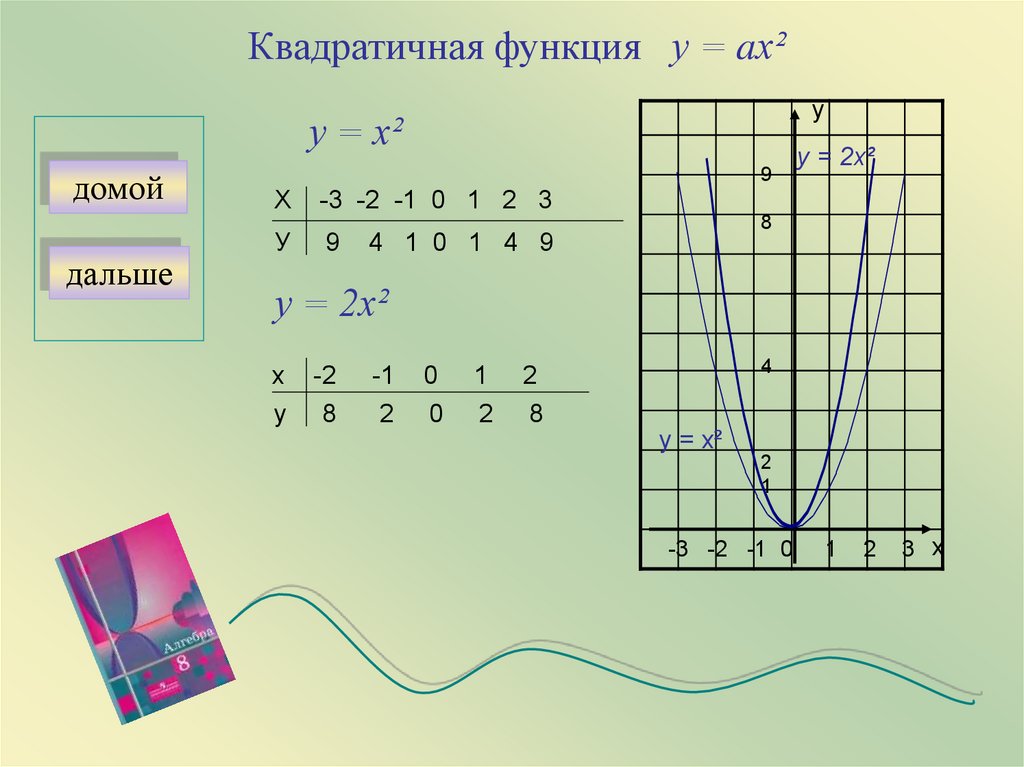
Квадратичная функция у = aх²
у
у = х²
домой
дальше
Х
У
9
у = 2х²
-3 -2 -1 0 1 2 3
9
8
4 1 0 1 4 9
у = 2х²
х
-2
-1
0
1
2
у
8
2
0
2
8
4
у = х²
2
1
-3 -2 -1 0
1
2
3 х

6.

домой
Квадратичная функция у = aх²
у = х²
дальше
х
-3 -2 -1 0 1 2 3
у
9
у=
4 1 0 1 4 9
1
2
9
8
х²
х
- 3 -2 -1 0 1
у
4,5 2 0,5 0 0,5 2 4,5
График функции у
2
3
= ах² получается
• растяжением в а раз, если а > 1
• сжатием в 1/а раз, если 0 < а < 1
графика функции у = х² от оси Ох вдоль
оси Оу.
у = х²
4
2
1
-3 -2 -1 0
1
у=
х²
2
1
2
3

7.

Квадратичная функция у = aх²
у
х
у
y 2x 2
домой
дальше
y 2x 2
х
-
Графики функций у = ах² и у = ах²
симметричны относительно оси абсцисс.

8.

Квадратичная функция у = a х²+ n
у = 2х²
у = 2х² - 3
домой
5
дальше
х
у
-2
5
-1
-1
0
-3
1
-1
График функции у = ах² + n
получается из графика функции у
2
5
= х²
с помощью параллельного переноса
вдоль оси Оу на
• n единиц вверх, если n > 0
• n единиц вниз, если n < 0.
-2 - 1 0
-1
1
2
у = 2 х² - 3
-3

9.

Квадратичная функция у = а(х –m)²
домой
у
у=0,5(х-3)²
у=0,5х²
у=0,5(х-3)²
дальше
График функции у = а(х – m)²
получается из графика
у = ах² сдвигом
вдоль оси Ох на
• m единиц вправо, если m > 0
• m единиц влево, если m < 0
0
1
3
х

10.

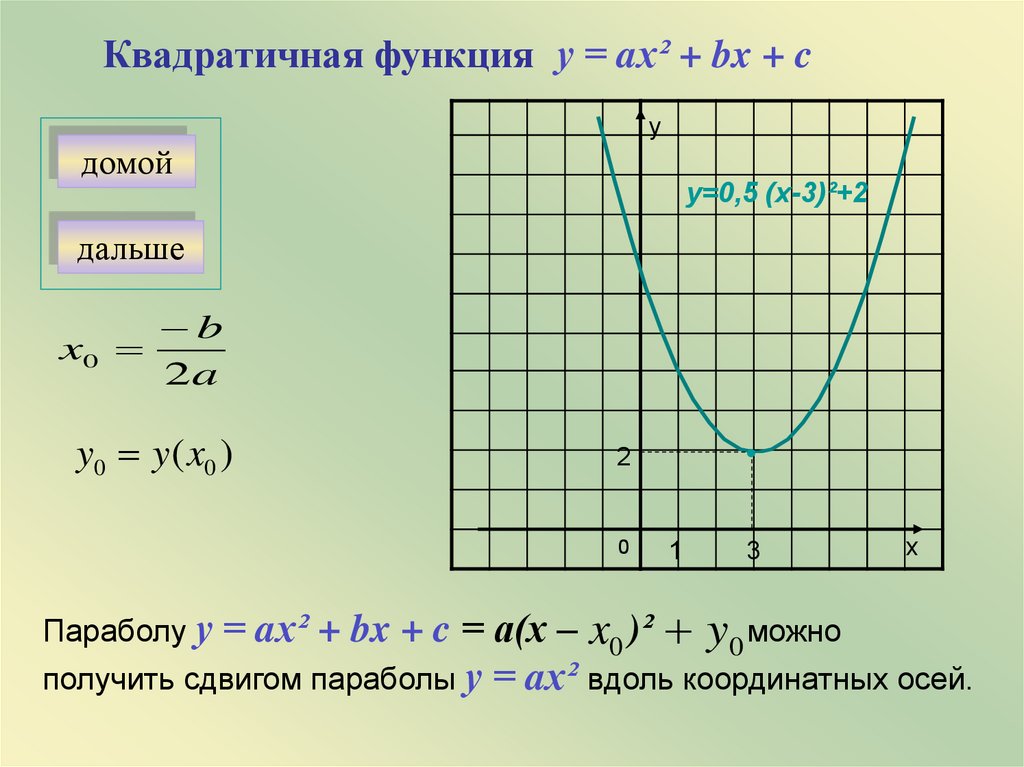
Квадратичная функция у = aх² + bx + c
у
домой
у=0,5 (х-3)²+2
дальше
b
x0
2a
y0 y ( x0 )
2
0
1
3
х
= aх² + bx + c = а(х – x0 )² y0 можно
получить сдвигом параболы у = aх² вдоль координатных осей.
Параболу у

11.

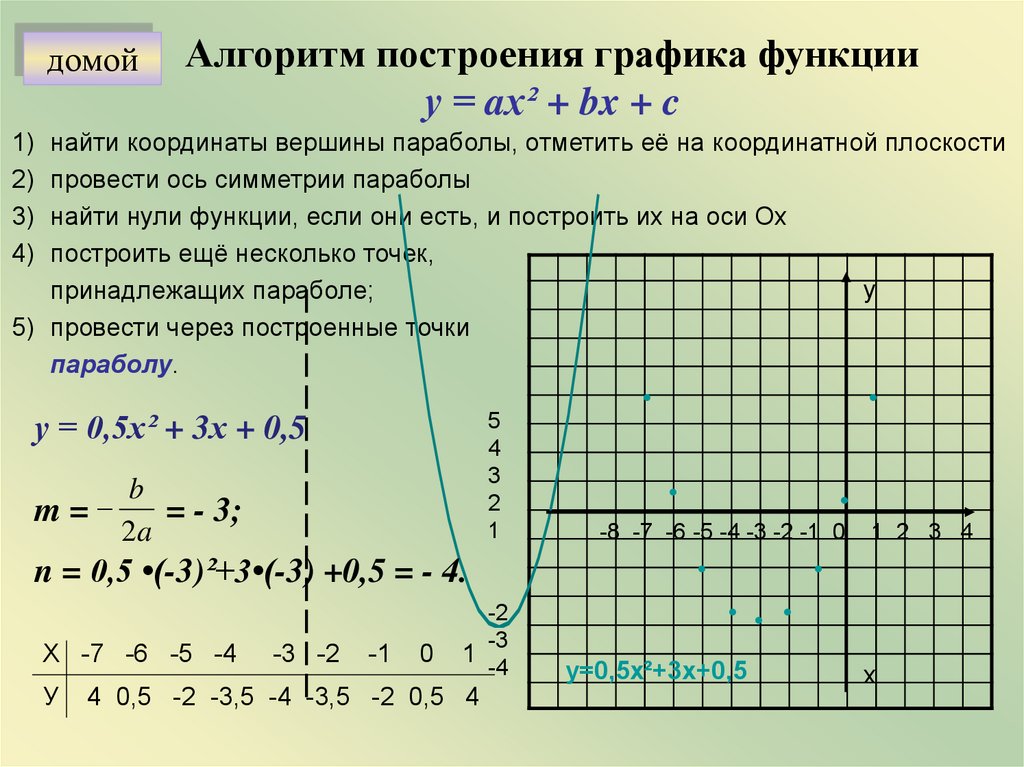
домой
Алгоритм построения графика функции
у = aх² + bx + c
найти координаты вершины параболы, отметить её на координатной плоскости
провести ось симметрии параболы
найти нули функции, если они есть, и построить их на оси Ох
построить ещё несколько точек,
у
принадлежащих параболе;
5) провести через построенные точки
параболу.
1)
2)
3)
4)
у = 0,5х² + 3х + 0,5
m=
5
4
3
2
1
b
= - 3;
2a
n = 0,5 •(-3)²+3•(-3) +0,5 = - 4.
Х -7 -6 -5 -4
У
-3 -2
-1
0
-2
-3
1 -4
4 0,5 -2 -3,5 -4 -3,5 -2 0,5 4
-8 -7 -6 -5 -4 -3 -2 -1 0
1 2 3 4
• •
у=0,5х²+3х+0,5
х

12.

Практикум
I вариант
домой
дальше
II вариант
1. Постройте график
1. Постройте график
функции у = - х²+2х+8. функции у = х²- 4х -5
2. Определите по
графику значение у
2. Определите по
графику значение у
при х = 2,5; -0,5.
при х = 2; -1.
3. Определите по
графику значение х,
соответствующее
значению у = 6; 0.
3. Определите по
графику значение х,
соответствующее
значению у = -9; 0.
4. Принадлежит ли данному графику точка А(2;8)?

13.

Тренажер
1
3
2
-3
3
3
4
-3
-3
5
6
3
домой
-3
Установите соответствие
между видом функции
и видом графика
у = х²-3
1
2
3
4
5
6
у = -х²+3
1
2
3
4
5
6
у = (х-3)²
1
2
3
4
5
6
у = -(х+3)²
1
2
3
4
5
6
у = (х+3)²
1
2
3
4
5
6
у=(х-3)²-3
1
2
3
4
5
6
дальше

14.

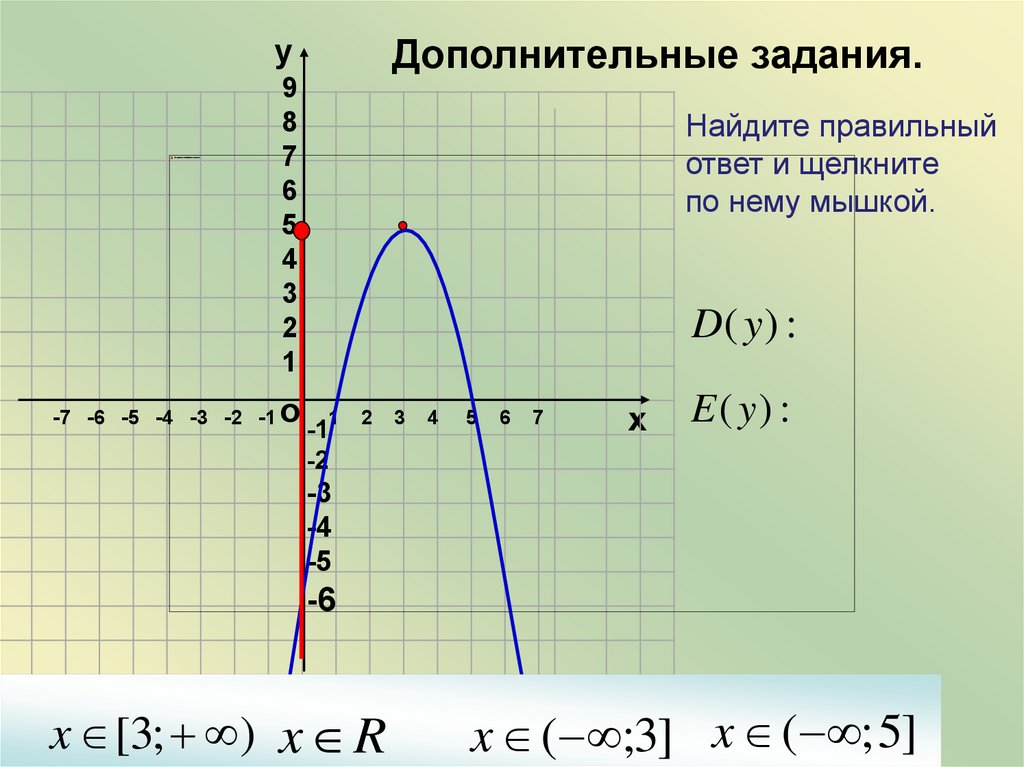
у
Дополнительные задания.
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
Найдите правильный
ответ и щелкните
по нему мышкой.
D( y ) :
о -11
2
3
4
5
6
7
х
E ( y) :
-2
-3
-4
-5
-6
x x [3[3;
x
(
;
5
]
x
(
;
3
]
R
x
(
;
5
]
; )) xx
x
(
;
3
]
R

15.

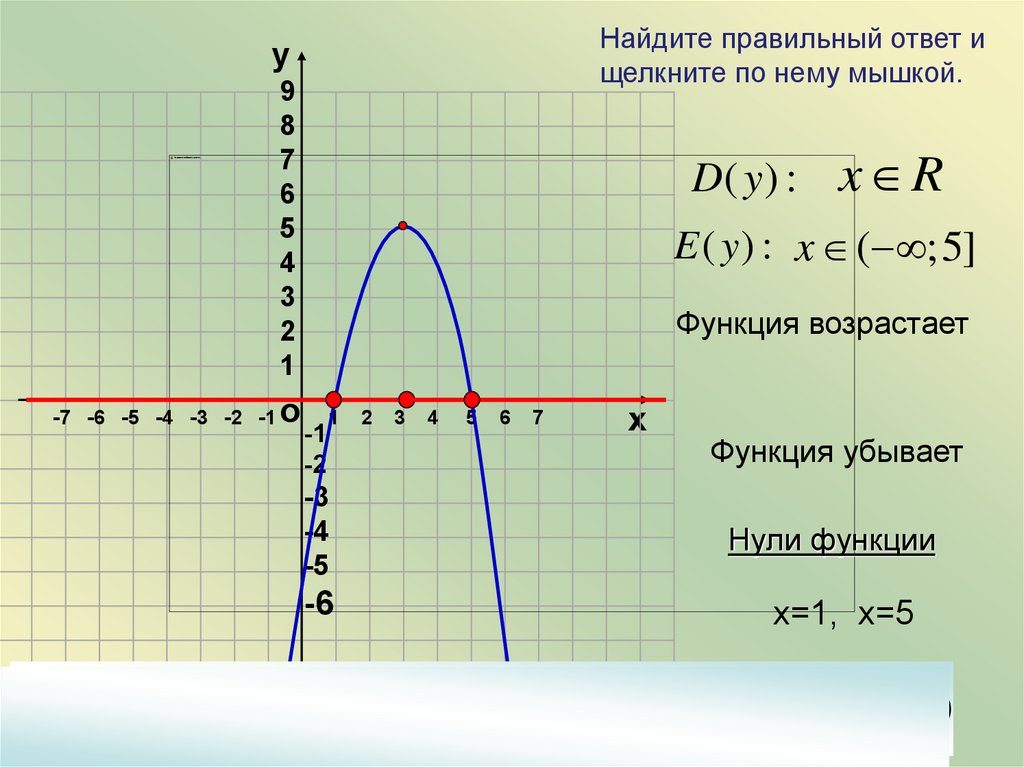
Найдите правильный ответ и
щелкните по нему мышкой.
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
D( y ) : x R
E ( y ) : x ( ; 5]
Функция возрастает
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
Функция убывает
Нули функции
х=1, х=5
;3)] xx (
[3;
xx
5;
((33;;
)) xх
;
; 5])
[(
; 3]) xx [3(

16.

Найдите правильный ответ и щелкните по нему мышкой.
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
Найти значения х, при
которых значения
функции положительны.
-1
-2
1
2
3
4
5
6
7
х
Найти значения х,
при которых значения
функции отрицательны.
-3
-4
-5
-6
(5;
xx ((51; 5) ) xх (
(
[1; 5;1]] xx (
;1)
(1; 5;1) ) x

17.

График какой функции изображен на рисунке?
Найдите правильный
ответ и щелкните
по нему мышкой.
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
у = 2x + 4
у = – x2 + 4
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
у = – 2x + 4
у = x2 – 4

18.

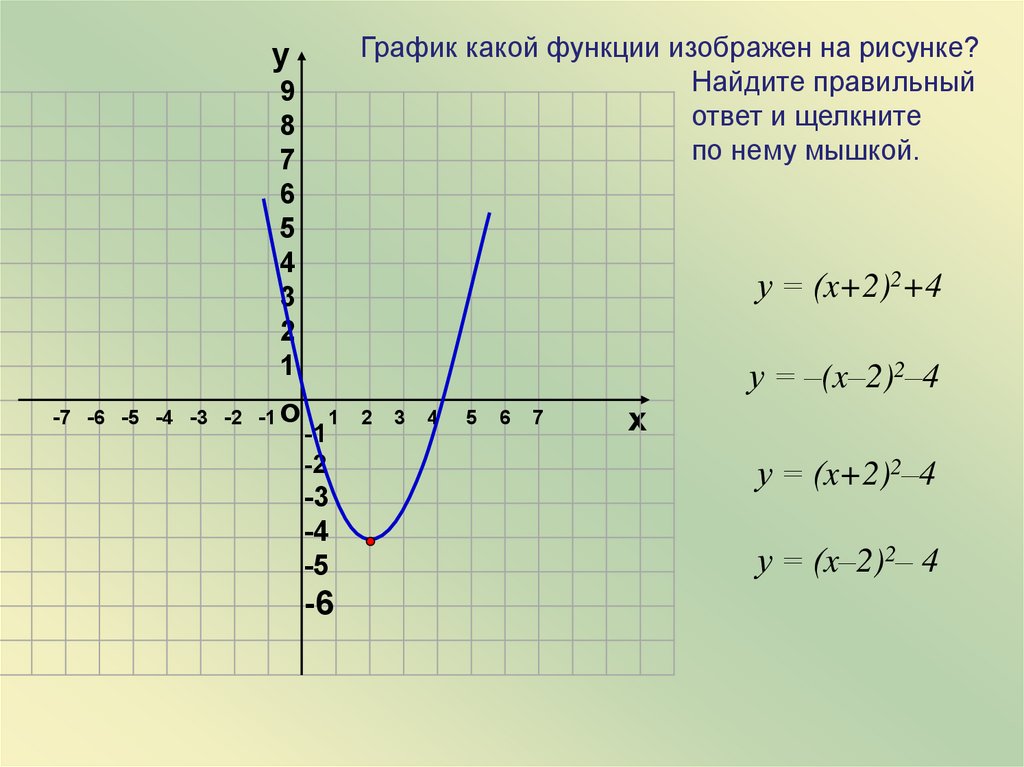
График какой функции изображен на рисунке?
Найдите правильный
ответ и щелкните
по нему мышкой.
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
у = (x+2)2+4
у = –(x–2)2–4
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
у = (x+2)2–4
у = (x–2)2– 4

19.

На рисунках показаны графики функций у=aх2+bx+с.
Укажите верную комбинацию.
у
а<0, D>0
a<0, D>0
у
a<0, D<0
a<0, D<0
х
a>0, D>0
a>0, D>0
a>0, D<0
a>0, D<0
у
у
a>0, D>0
a>0, D=0
a>0, D=0
a>0, D<0
a<0, D>0
a<0, D=0
х
0
0
х
0
a<0, D<0
a<0, D=0
х

20.

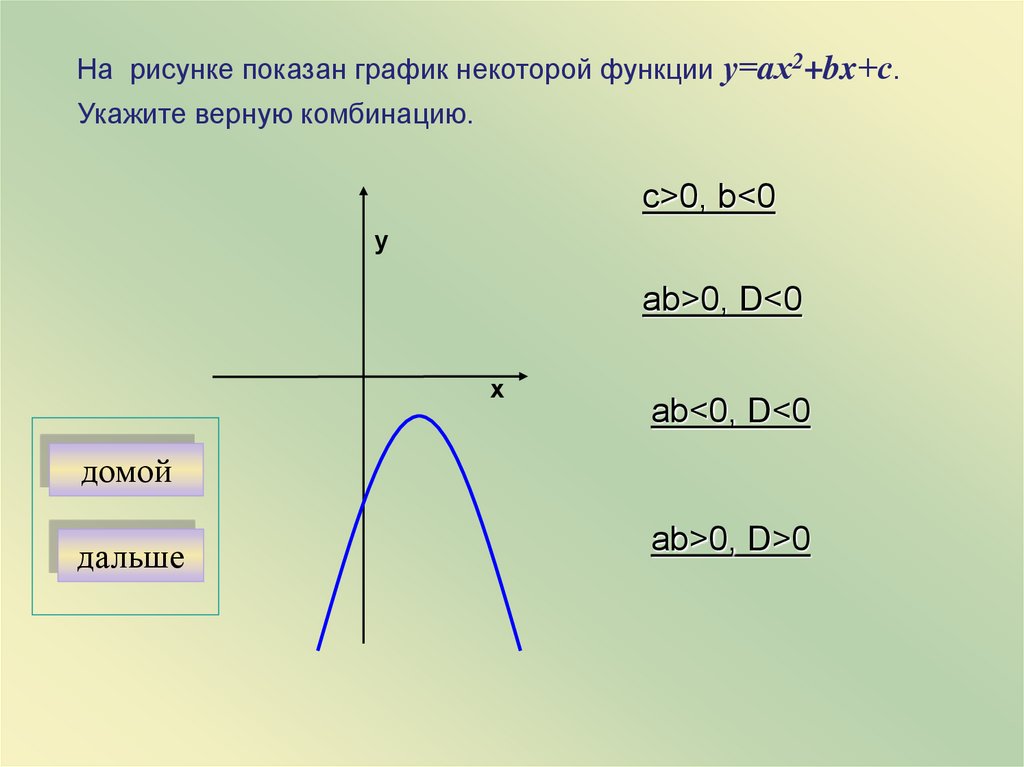
На рисунке показан график некоторой функции у=aх2+bx+с.
Укажите верную комбинацию.
c>0, b<0
у
ab>0, D<0
х
ab<0, D<0
домой
дальше
аb>0, D>0

21.

Хотите продолжить?
да
нет
домой

22.

Попробуйте ещё раз
домой

23.

24.

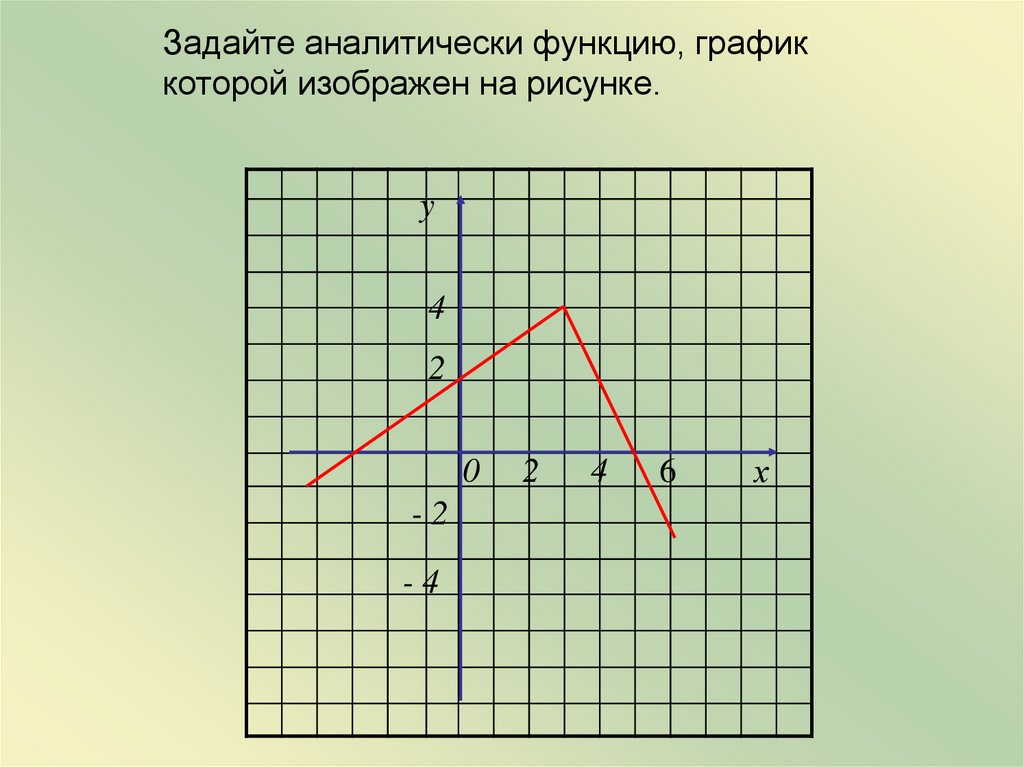
Задайте аналитически функцию, график
которой изображен на рисунке.
y
4
2
0
-2
-4
2
4
6
х