Similar presentations:
Случайные события и их вероятности. Решение задач
1.
Шайдурова Надежда МихайловнаУчитель математики
Стаж: 28 лет
Образование: высшее
Категория: высшая
ОУ «Баевская МСОШ»
Алтайского края
2011 г.
2.
Тема: Случайные события и их вероятностиЦель:
Обобщить и проверить знания полученные при
изучении темы, изучить понятия
противоположного события, несовместные
события, формулу вычисления вероятности
противоположного события,
совершенствовать умения и навыки решения
задач.
3.
Проверка решения домашней задачи:актуализация знаний учащихся.
Случайным образом выбрали двузначное число.
Найти вероятность того, что оно: оканчивается 0,
состоит из одинаковых цифр.
Решение:
1) Общее число двузначных чисел равно
n = 9 * 10 =90
2) выбор каждого является равновозможным
3) А – выбранное число оканчивается нулём
4) находим количество исходов опыта, в котором
наступает событие А, N(A) = 9,
числа 10, 20, 30, 40, ……90.
5) Р(А) = 9 : 90 = 0,1
4.
При втором условии:1) Общее число двузначных чисел равно 90.
2) выбор каждого является равновозможным
3) В – выбранное число состоит из
одинаковых чисел
4) находим количество исходов опыта, в
котором наступает событие В, N(В) = 9,
числа 11, 22, 33, 44, ……99.
5) Р(В) = 9 : 90 = 0,1
Ответ: 0,1; 0,1
5.
Актуализация знаний учащихся.Проверка домашнего задания:
письменный теоретический опрос:
1) Какие события называются достоверными,
случайными. Невозможными?
2) Классическое определение вероятности.
3) Чему равна вероятность достоверного
события, невозможного события?
4) Записать формулу нахождения вероятности
события А, т.е.
Р(А) =
6.
Задача:5) Задача:
Случайным образом выбрали двузначное
число. Найдите вероятность того, что
оно
1 вариант: больше 27 и меньше 46
2 вариант: больше 35 и меньше 52
7.
Решение задач самостоятельной работы:Общее число двузначных чисел равно: n = 9 * 10 = 90
Выбор каждого является равновозможным.
Количество благоприятствующих исходов каждого из этих
событий находим по формуле: Р(А) = N (A) : N
Вариант 1
N (A) = 18 (числа 28, 29,.....45)
Р (А) = 18 : 90 = 1/5
Ответ: 1/5
Вариант 2
N (A) = 16 (числа от 36, 37......51)
Р (А) = 16 : 90 = 8 / 45
Ответ: 8/45
8.
АОпределения, теоремы:
1) Событие В называют противоположным
событием А и обозначают В=А, если событие В
происходит, тогда и только тогда, когда не
происходит событие А.
А
Обозначают символом
Теорема: Для нахождения вероятности
противоположного события следует из
единицы
вычесть вероятность самого события:
А
Р(
)=1-Р(А)
2) Событие А и В называются несовместными,
если они не могут происходить одновременно
9.
Определения, теоремы:Теорема: Вероятность
наступления хотя одного
из двух несовместных
событий равна сумме их
вероятностей.
Если А и В
несовместны,
то Р(А+В)=Р(А)+Р(В)
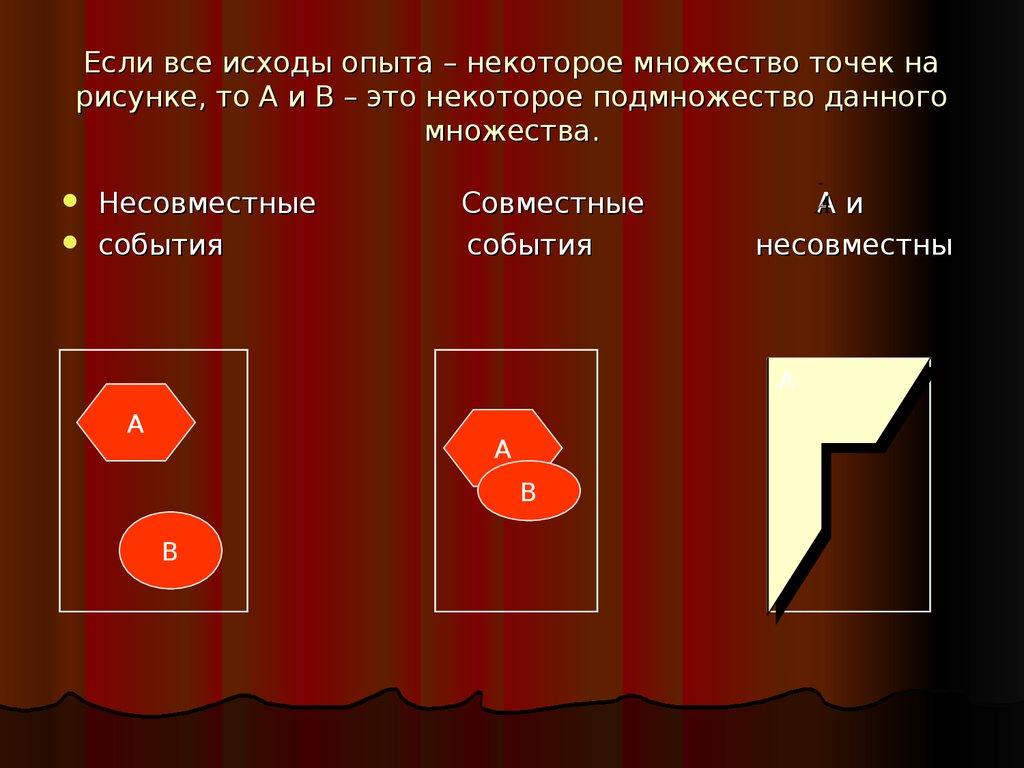
10.
Если все исходы опыта – некоторое множество точек нарисунке, то А и В – это некоторое подмножество данного
множества.
Несовместные
события
Совместные
события
Аи
А
несовместны
А
АА
А
А
В
В
11.
Вероятность суммы любого числа попарно несовместныхсобытий равна сумме вероятности этих событий.
Р(А+В+С+Д……)= Р(А)+Р(В)+Р(С)+Р(Д)+…..
Схема:
С
А
В
Д
12.
Тест: с последующей самопроверкойВариант 1
Вариант 2
1)В мешке лежат 11 шаров:
3 синих, 4 зелёных. 4
красных.
События:
1)В ящике лежат 12
кубиков: 5 красных, 3
синих, 4зелёных.
События:
А – из мешка вынули 4
А-
шара и все синие. Оцените
какое событие? невозможное, случайное,
достоверное,
противоположное.
из ящика вынули 5
кубиков, и все зелёные.
Оцените какое событие?
- невозможное,
случайное, достоверное,
несовместное.
В- из мешка вынули 4 шара, В – из ящика вынули 3
и все они красные. Оцените
какое событие? невозможное, случайное,
кубика, и все они синие.
Оцените какое событие?
- невозможное,
13.
Тест:Вариант 1
С - из мешка вынули 5
шаров и среди них не
оказалось белого шара.
Оцените какое событие?
- невозможное,
случайное, достоверное,
противоположное.
2) События А и В
противоположные.
Вероятность события А
равна
Р(А)=7/13, тогда
вероятность события В
равна:
1) 7/13 2) 20/13
Вариант 2
С – из ящика вынули 9
кубиков, и среди них не
оказалось сиреневого
шара.
Оцените какое событие? невозможное,
случайное, достоверное,
несовместное.
2) События А и В
несовместны.
Р(А)=3/28
Р(В)= 11/28
Вероятность суммы событий
А и В равна:
1) 8/28 2) 2/7
14.
Самопроверка:Задачи
№1
№2
Вариант 1
А(1),
3) = 6/13
невозможное
В(2), случайное
С(3), достоверное
Вариант 2
А(3),
невозможное
В(1), случайное
С(2), достоверное
3) = 1/2
15.
Практическая работа: решение задачПорядок выполнения работы:
Каждый ученик получает индивидуально задачи
определённого уровня и решает:
1 уровень
2 уровень
3 уровень
По окончанию работы проводится самопроверка:
Оценка результатов
16.
Решение задачи 1 уровня3
N = C 36 =
(и с х о д о в )
С о б ы ти е А – « ср ед и 3 кар т н ет к р есто в о го к о р о л я»
N ( А ) = C 3 35 =
Р (А ) = 1 – Р (А ) = 1 О твет:
=1-
=
17.
Решение задачи 2 уровня:И з 3 6 э л е м е н т о в в о зм о ж н о п о л у ч е н и е : N = C 536 и с х о д о в .
А – «будет среди 5карт хотя бы одн а карта п иковой м асти ».
А « с р е д и 5 к а р т н и о д н о й п и к о в о й к а р т ы », т .е . в с е о с т а л ь н ы е м а с т и , к р о м е п и к и (9 к а р т
п и к о в ы х ).
36 – 9 = 27 карт без п и ковой м асти .
5
З н а ч и т N (А ) = = C 27
Н ай дём вероятн ость собы ти я А :
Р (А ) -=
5
= C 27 : C
5
36
=
В ероятн ость собы ти й А :
Р ( А ) = 1 – Р ( А ) = 1 – 0 , 2 1 4 = 0 ,7 8 6
= 0 ,2 1 4
18.
Решение задачи 3 уровня:А – «и н тересую щ ее н ас собы ти е, он о н аступ ает, когда и з 5 ручек 3 – красн ы е и 2 – си н и е.
И з 1 0 к р а с н ы х р у ч е к – 3 р у ч к и м о ж н о в ы б р а т ь C 3 10 с п о с о б а м и , а и з 1 1 с и н и х р у ч е к – 2
р у ч к и C 211 с п о с о б а м и . В ы б о р р у ч е к с ч и т а е м н е за в и с и м ы м . В с е г о 2 1 р у ч к а . N = C 521
сп особам и вы бора.
П о п рави лу ум н ож ен и я п олучаем , что н уж н ы й н ам состав ручек м ож н о вы брать
N (А ) = C 3 10 * C 211 с п о с о б а м и . П о с ч и т а е м в е р о я т н о с т ь :
Р (А ) -=
О т в е т : 0 ,3 2 4
= C 3 10 * C 211 : C 521 =
*
=
19.
Задачи для устной работы:С обы тия А и В н есовм естны .
Р (А ) =
, Р (В ) =
В ероятн ость сум м ы собы тий А и В равн а:
1)
*
2)
3)
4)
, обоснуй те ответ.
В о д н о й и гр е в б аск етб о л м еж д у к о м ан д ам и 9 « а» и 9 « б »:
С обытия:
А – ком ан да 9 «а » п роиграла, ком ан да 9»б» пр оиграла, являю тся:
1) н есовм естн ы м и
2) совм естны м и , ответ обосн уйте.
В - к о м ан д а 9 « а» вы и гр ал а, к о м ан д а 9 » б » п р о и гр ал а, яв л яю тся:
1) н есовм естн ы м и
2) совм естны м и , ответ обосн уйте.
20.
Домашняя работаДома:
1) выучить определения, теоремы
2) задача:
Из чисел 1,2,3,4,5 одновременно выбирают три.
Найдите вероятность того, что:
а) существует прямоугольный треугольник с
такими сторонами;
б) существует произвольный треугольник с
такими сторонами;
в) произведение этих чисел оканчивается на 0;
Г) их сумма меньше 10
21.
Спасибо за внимание.Успехов
в решении задач




















 mathematics
mathematics








