Тарифный план «Просто как день»

1.

Вариант № 23449740
1. По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта
абонента 16 рублей. Если на счету осталось меньше 16 рублей, то на следующее утро номер блокируют
до пополнения счёта. Сегодня утром у Лизы на счету было 700 рублей. Сколько дней (включая
сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
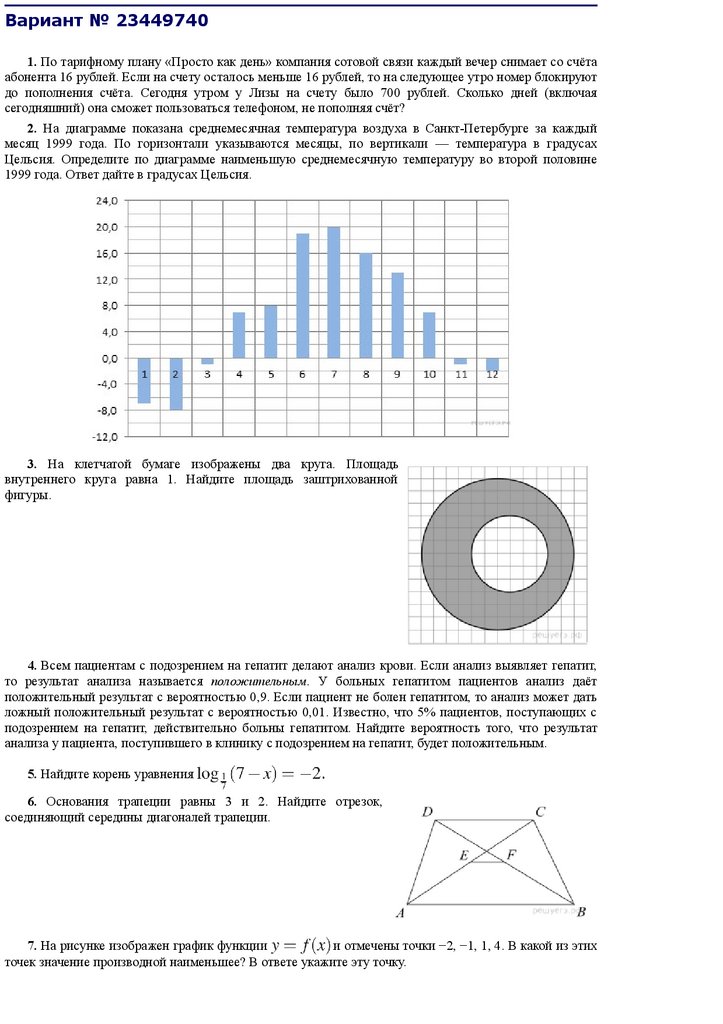
2. На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый
месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах
Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине
1999 года. Ответ дайте в градусах Цельсия.
3. На клетчатой бумаге изображены два круга. Площадь
внутреннего круга равна 1. Найдите площадь заштрихованной
фигуры.
4. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит,
то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт
положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать
ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с
подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат
анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
5. Найдите корень уравнения
6. Основания трапеции равны 3 и 2. Найдите отрезок,
соединяющий середины диагоналей трапеции.
7. На рисунке изображен график функции
и отмечены точки −2, −1, 1, 4. В какой из этих
точек значение производной наименьшее? В ответе укажите эту точку.

2.

8. В сосуд, имеющий форму правильной треугольной призмы, налили воду.
Уровень воды достигает 80 см. На какой высоте будет находиться уровень
воды, если ее перелить в другой такой же сосуд, у которого сторона основания
в 4 раза больше, чем у первого? Ответ выразите в см.
9. Найдите значение выражения
, если
,а
10. Высота над землeй подброшенного вверх мяча меняется по закону
,
где – высота в метрах, – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет
находиться на высоте не менее трeх метров?
11. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая
отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы,
какую второй – за три дня?
12. Найдите точку максимума функции
13. Решите уравнение:
14. В кубе ABCDA1B1C1D1 все ребра равны 6.
а) Докажите, что угол между прямыми AC и BC1 равен 60°.
б) Найдите расстояние между прямыми AC и BC1.
15. Решите неравенство
16. Точки A1, B1 и C1 — середины сторон соответственно BC, AC и AB остроугольного
треугольника ABC.
а) Докажите, что отличная от A1 точка пересечения окружностей, описанных около треугольников
A1CB1 и A1BC1, лежит на окружности, описанной около треугольника B1AC1.
б) Известно, что AB = AC = 10 и BC = 12. Найдите радиус окружности, вписанной в треугольник,
вершинами которого являются центры окружностей, описанных около треугольников A1CB1, A1BC1 и
B1AC1.
17. 1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита
следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга
(то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий
выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три
раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395
800 рублей?

3.

18. Найти все значения параметра
при каждом из которых среди значений функции
есть ровно одно целое число.
19. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два
учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное
количество баллов. оказалось, что в каждой школе средний балл был целым числом. После этого один
из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были
пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 вырасти в два раза?
б) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог
ли первоначальный балл в школе № 2 равняться 1?
в) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%.
Найдите наименьшее значение первоначального среднего балла в школе № 2.