Similar presentations:
Элементы алгебры логики. Логические операции. Математические основы информатики
1.
Элементы алгебрылогики.
Логические операции
Математические основы информатики
2.
Элементы алгебры логики. Логические операции1
2
3
Инверсия.
Конъюнкция.
Дизъюнкция.
3.
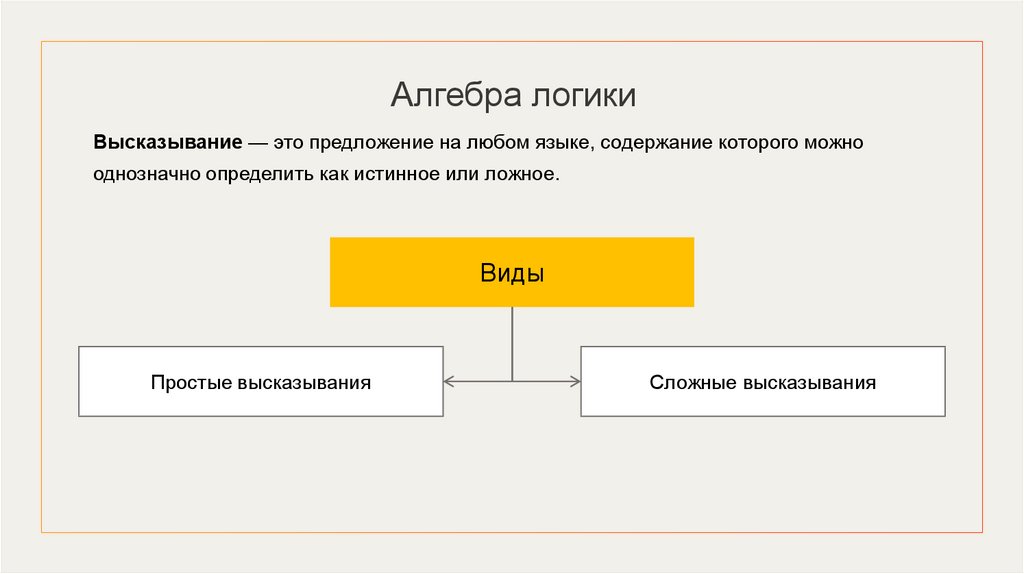
Алгебра логикиВысказывание — это предложение на любом языке, содержание которого можно
однозначно определить как истинное или ложное.
Виды
Простые высказывания
Сложные высказывания
4.
ВысказыванияПростое высказывание − это высказывание, в котором никакая его часть сама
не является высказыванием.
Минск − столица Беларуси.
Монитор является устройством
хранения информации.
5.
ВысказыванияСложные (составные) высказывания − это высказывания, которые строятся из
простых с помощью логических операций.
В интернете можно найти много полезной информации и пообщаться с друзьями.
В интернете можно найти много
полезной информации.
В интернете можно пообщаться с
друзьями.
6.
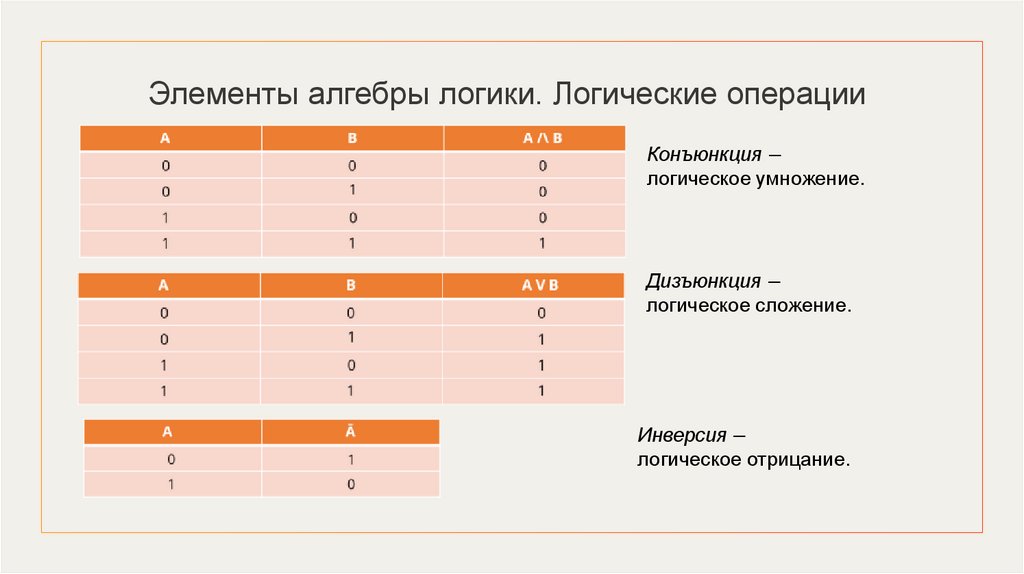
Основные логические операцииНазвание логической операции
Логическая связка
Инверсия
«не»; «неверно, что»
Конъюнкция
«и»; «а»; «но»; «хотя»
Дизъюнкция
«или»
Логическая связка − это союзы или выражения, которые употребляются
в естественном языке для соединения простых высказываний в сложные.
7.
Основные логические операцииНазвание логической операции
Логическая связка
Инверсия
«не»; «неверно, что»
Конъюнкция
«и»; «а»; «но»; «хотя»
Дизъюнкция
«или»
Логическая связка − это союзы или выражения, которые употребляются
в естественном языке для соединения простых высказываний в сложные.
8.
Способы обозначения истинности и ложностиИстина
И
True
T
1
Ложь
Л
False
F
0
9.
Логические операцииКонъюнкция − это логическая операция, которая объединяет два высказывания в
одно новое, которое будет являться истинным тогда и только тогда, когда оба
исходных высказывания истинны.
Conjunctio − «союз, связь».
Пример:
А = «у квадрата 4 стороны».
В = «у ромба 4 стороны».
А И В = «у квадрата 4 стороны и у ромба 4 стороны».
10.
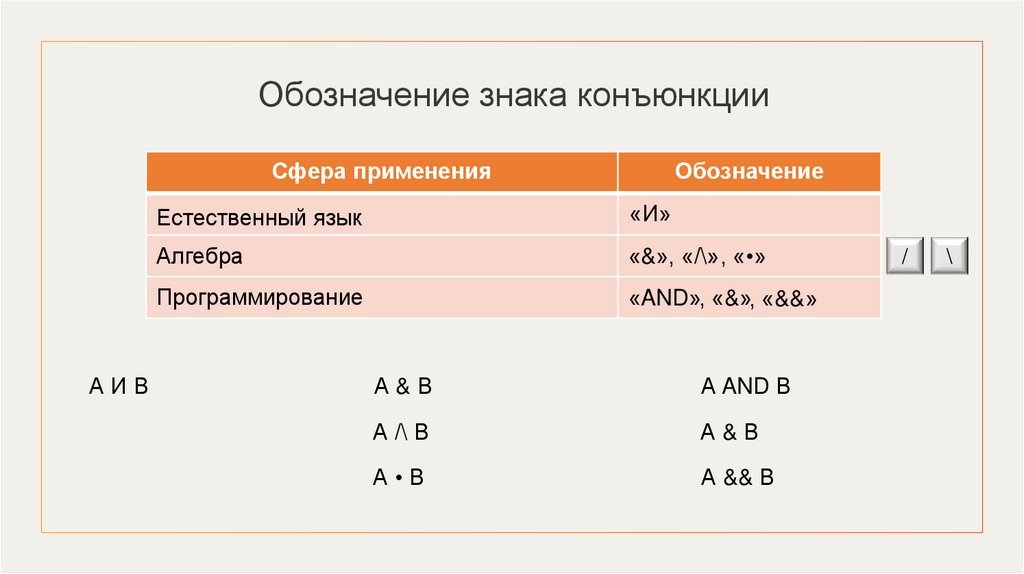
Обозначение знака конъюнкцииСфера применения
АИВ
Обозначение
Естественный язык
«И»
Алгебра
«&», «/\», «•»
Программирование
«AND», «&», «&&»
А&В
А AND В
А /\ В
А&В
А•В
А && В
/
\
11.
Таблица истинностиA
Дано: А, В.
А−
А=1
А−
А=0
B
A /\ B
12.
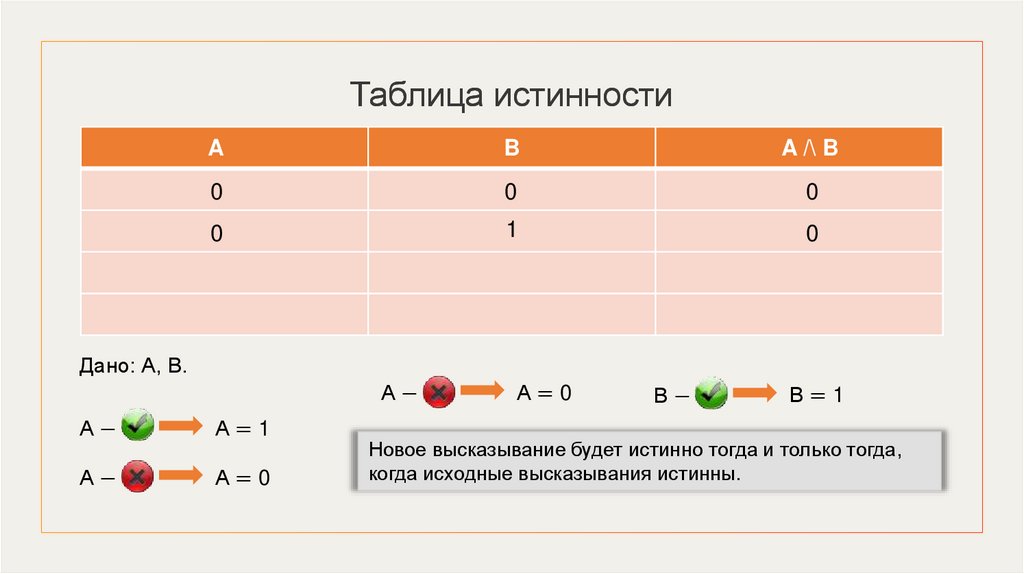
Таблица истинностиA
B
A /\ B
0
0
0
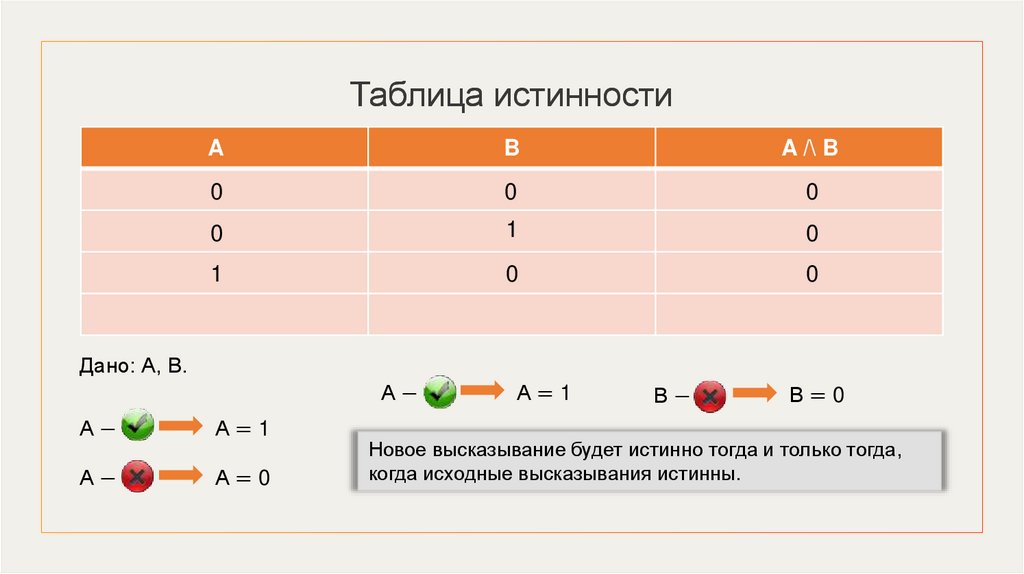
Дано: А, В.
А−
А−
А=1
А−
А=0
А=0
В−
В=0
Новое высказывание будет истинно тогда и только тогда,
когда исходные высказывания истинны.
13.
Таблица истинностиA
B
A /\ B
0
0
0
0
1
0
Дано: А, В.
А−
А−
А=1
А−
А=0
А=0
В−
В=1
Новое высказывание будет истинно тогда и только тогда,
когда исходные высказывания истинны.
14.
Таблица истинностиA
B
A /\ B
0
0
0
0
1
0
1
0
0
Дано: А, В.
А−
А−
А=1
А−
А=0
А=1
В−
В=0
Новое высказывание будет истинно тогда и только тогда,
когда исходные высказывания истинны.
15.
Таблица истинностиA
B
A /\ B
0
0
0
0
1
0
1
0
0
1
1
1
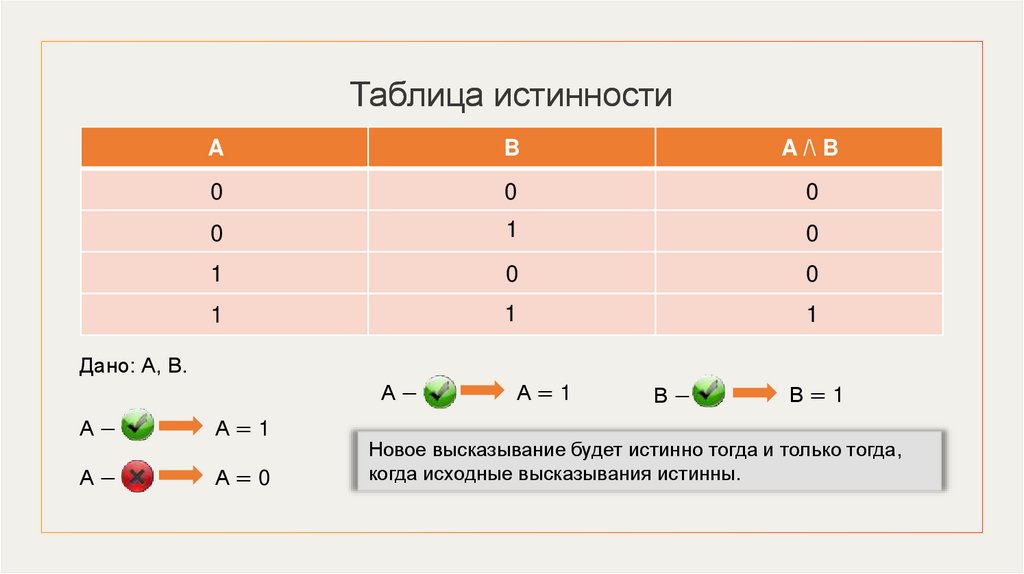
Дано: А, В.
А−
А−
А=1
А−
А=0
А=1
В−
В=1
Новое высказывание будет истинно тогда и только тогда,
когда исходные высказывания истинны.
16.
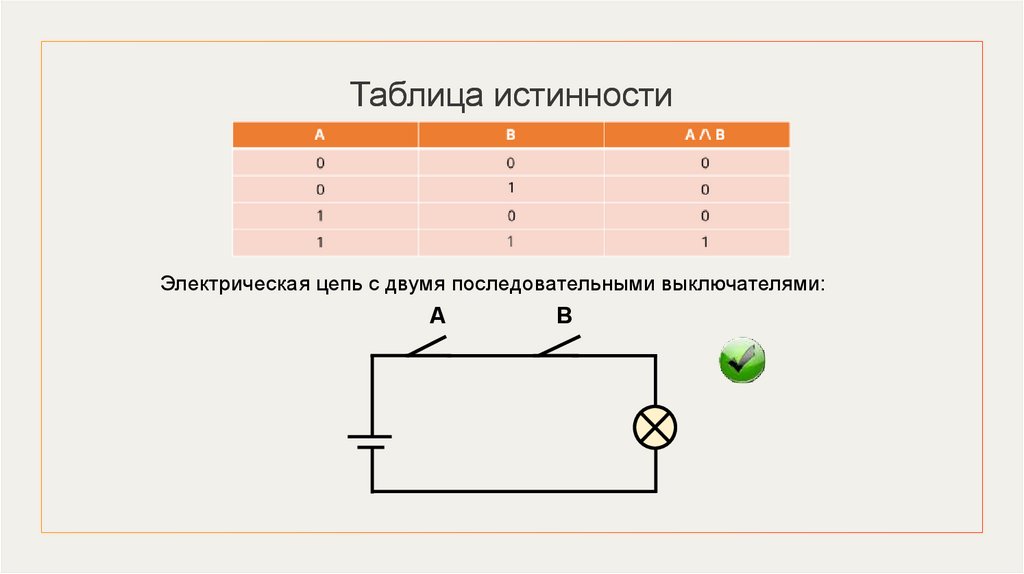
Таблица истинностиЭлектрическая цепь с двумя последовательными выключателями:
А
В
17.
Таблица истинностиA
B
A /\ B
0
0
0
0
1
0
1
0
0
1
1
1
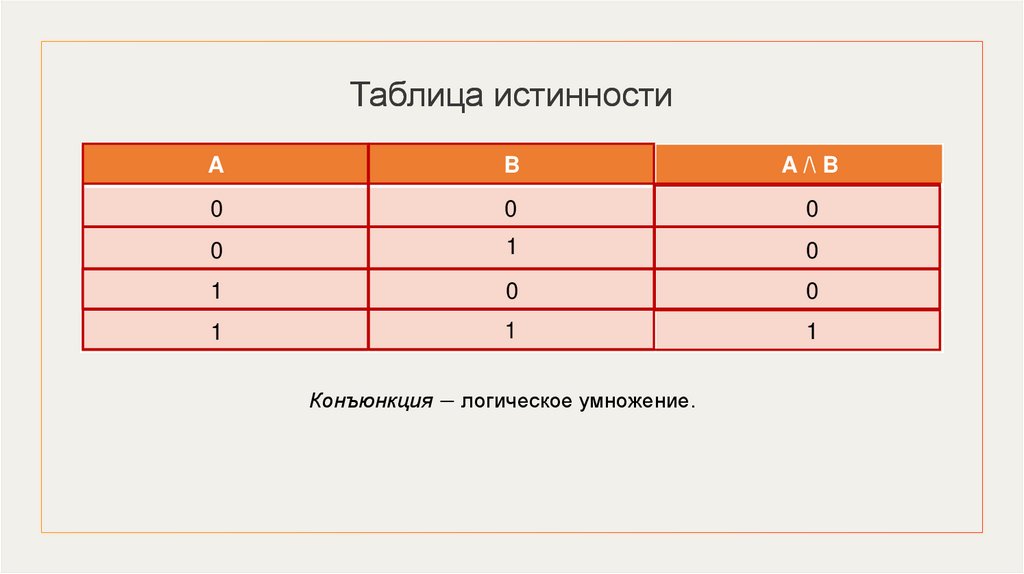
Конъюнкция − логическое умножение.
18.
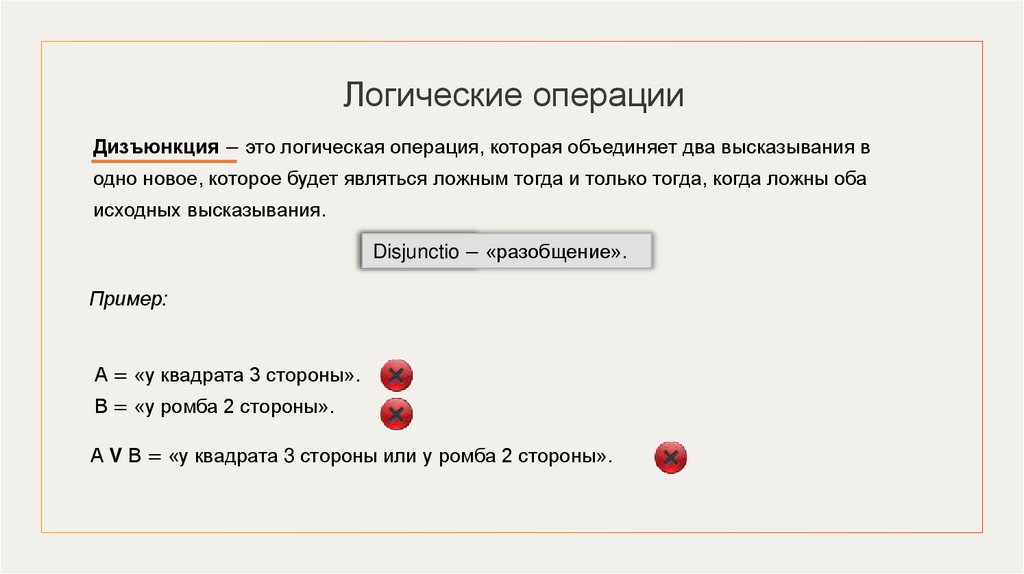
Логические операцииДизъюнкция − это логическая операция, которая объединяет два высказывания в
одно новое, которое будет являться ложным тогда и только тогда, когда ложны оба
исходных высказывания.
Disjunctio − «разобщение».
Пример:
А = «у квадрата 3 стороны».
В = «у ромба 2 стороны».
А V В = «у квадрата 3 стороны или у ромба 2 стороны».
19.
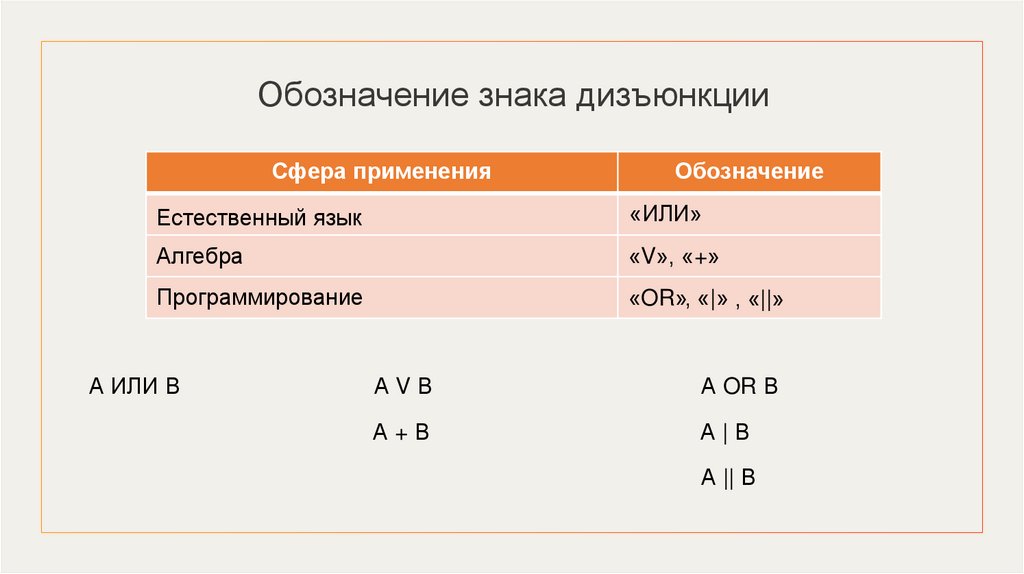
Обозначение знака дизъюнкцииСфера применения
Обозначение
Естественный язык
«ИЛИ»
Алгебра
«V», «+»
Программирование
«OR», «|» , «||»
А ИЛИ В
АVВ
А OR В
А+В
А|В
А || В
20.
Таблица истинностиA
Дано: А, В.
А−
А=1
А−
А=0
B
AVB
21.
Таблица истинностиA
B
AVB
0
0
0
Дано: А, В.
А−
А−
А=1
А−
А=0
А=0
В−
В=0
Новое высказывание будет ложно тогда и только тогда,
когда ложны исходные высказывания.
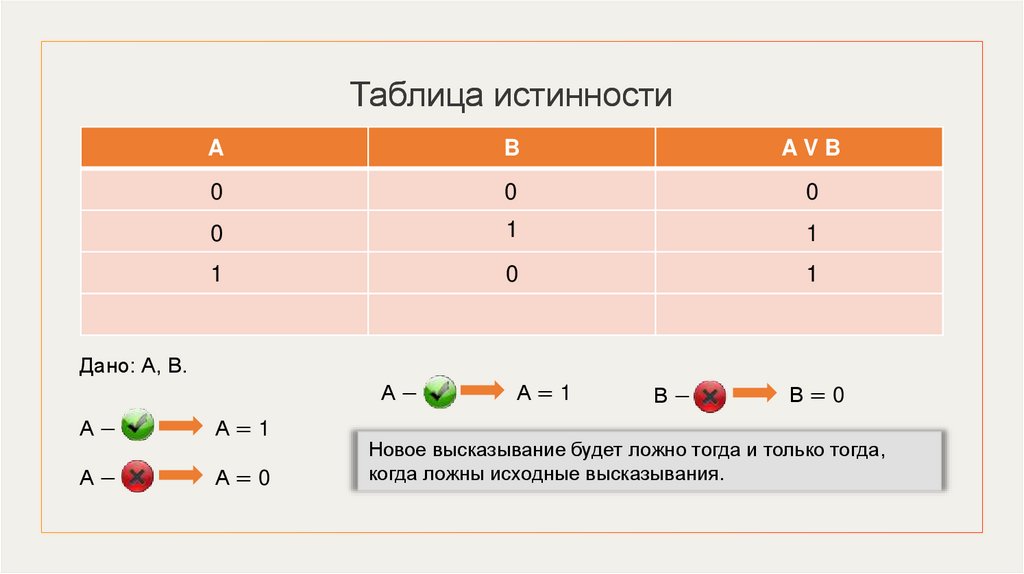
22.
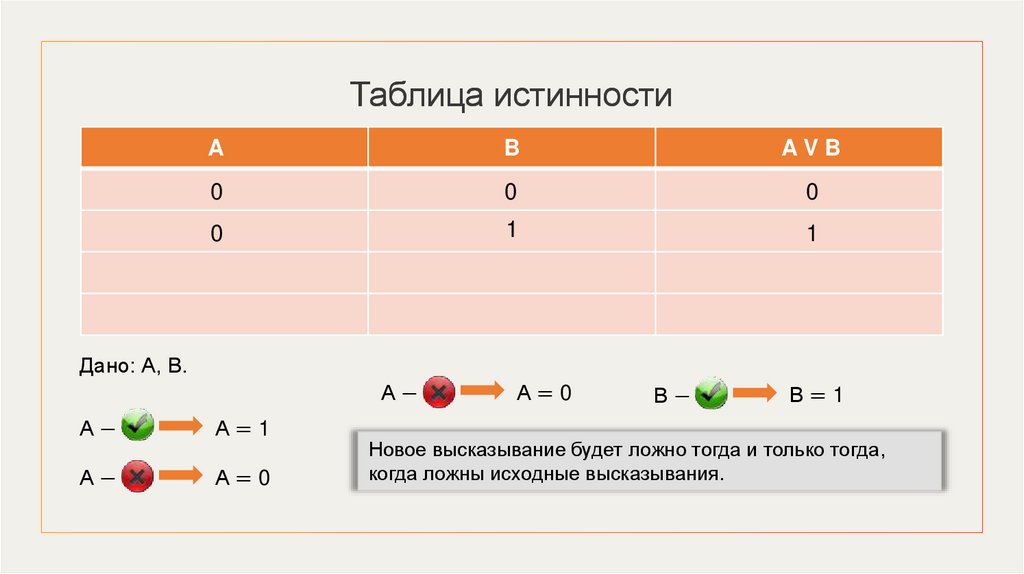
Таблица истинностиA
B
AVB
0
0
0
0
1
1
Дано: А, В.
А−
А−
А=1
А−
А=0
А=0
В−
В=1
Новое высказывание будет ложно тогда и только тогда,
когда ложны исходные высказывания.
23.
Таблица истинностиA
B
AVB
0
0
0
0
1
1
1
0
1
Дано: А, В.
А−
А−
А=1
А−
А=0
А=1
В−
В=0
Новое высказывание будет ложно тогда и только тогда,
когда ложны исходные высказывания.
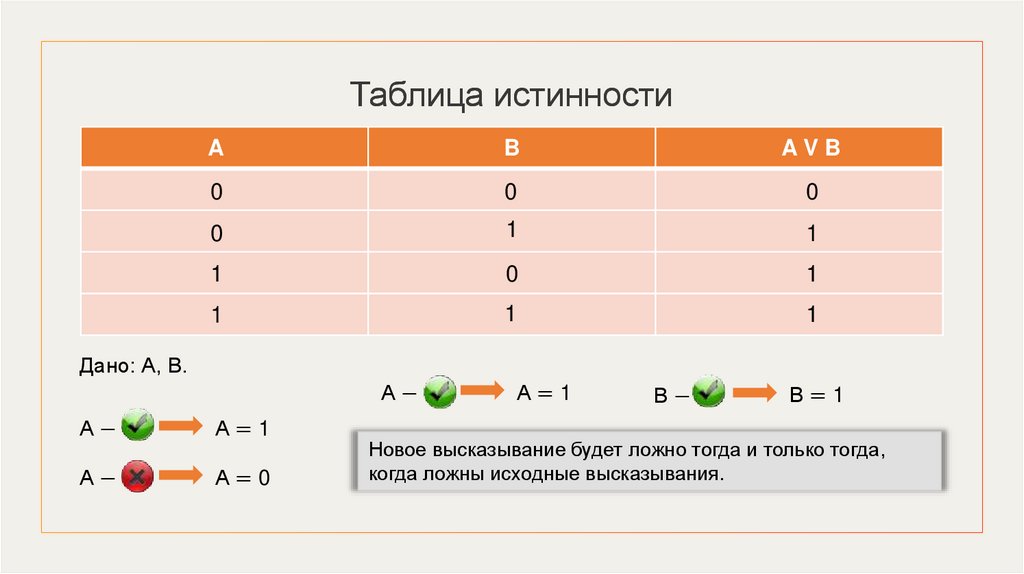
24.
Таблица истинностиA
B
AVB
0
0
0
0
1
1
1
0
1
1
1
1
Дано: А, В.
А−
А−
А=1
А−
А=0
А=1
В−
В=1
Новое высказывание будет ложно тогда и только тогда,
когда ложны исходные высказывания.
25.
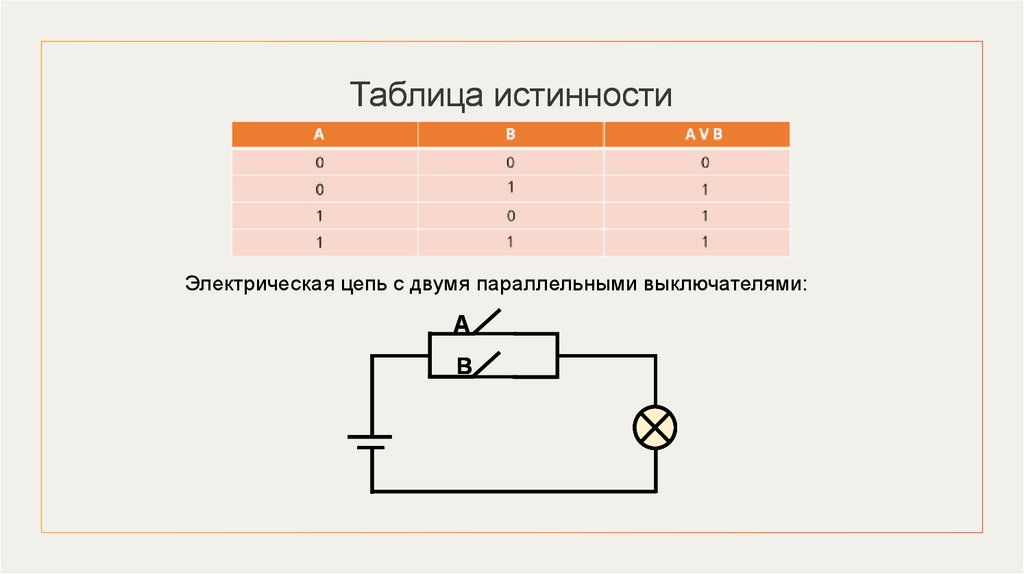
Таблица истинностиЭлектрическая цепь с двумя параллельными выключателями:
А
В
26.
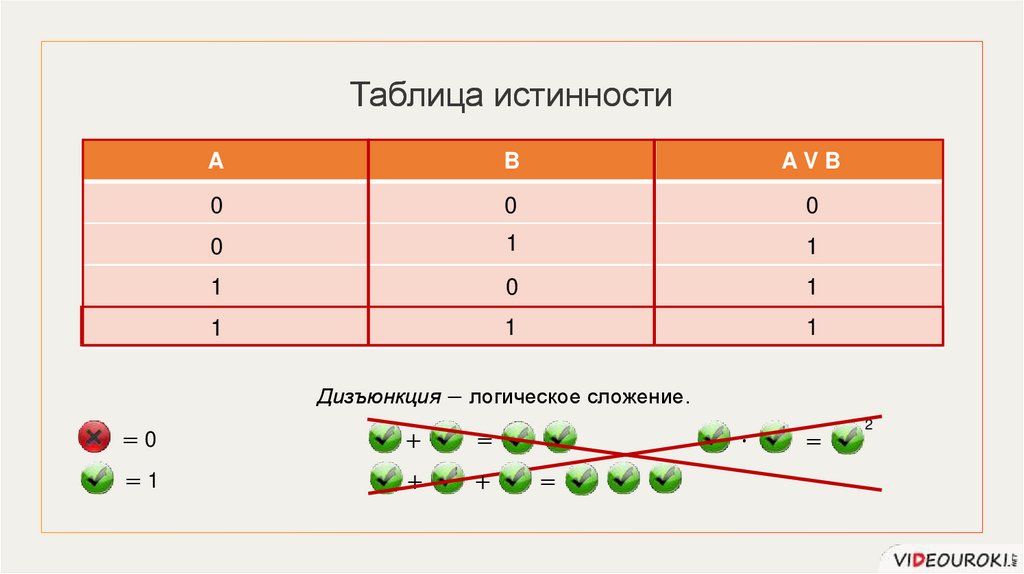
Таблица истинностиA
B
AVB
0
0
0
0
1
1
1
0
1
1
1
1
Дизъюнкция − логическое сложение.
=0
+
=
=1
+
+
∙
=
=
2
27.
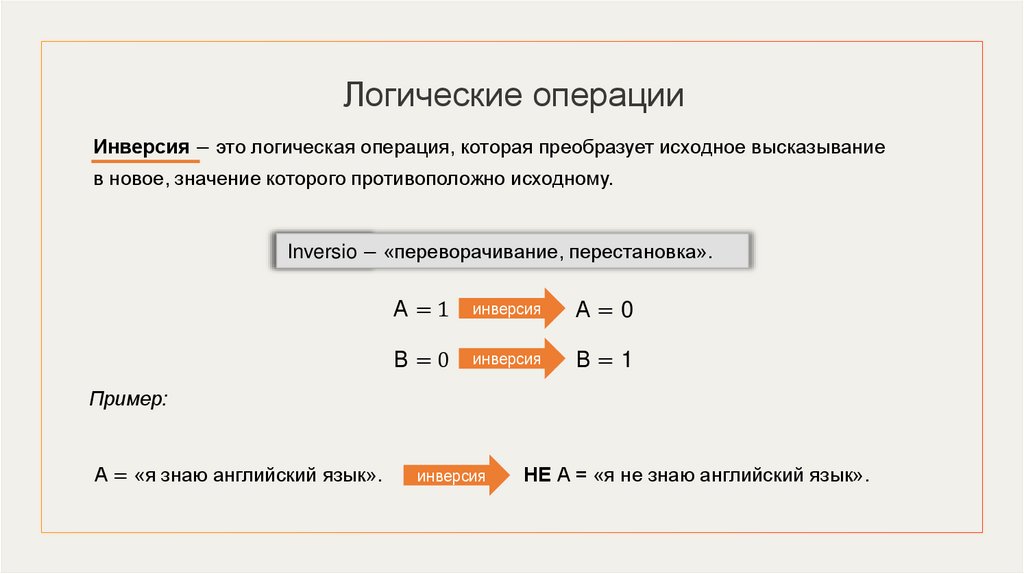
Логические операцииИнверсия − это логическая операция, которая преобразует исходное высказывание
в новое, значение которого противоположно исходному.
Inversio − «переворачивание, перестановка».
А=1
инверсия
А=0
В=0
инверсия
В=1
Пример:
А = «я знаю английский язык».
инверсия
НЕ А = «я не знаю английский язык».
28.
Обозначение знака инверсииСфера применения
Обозначение
Естественный язык
«НЕВЕРНО, ЧТО», «НЕ»
Алгебра
«¬», «¯»
Программирование
«NOT»
НЕВЕРНО, ЧТО А
¬А
НЕ А
Ā
NOT A
29.
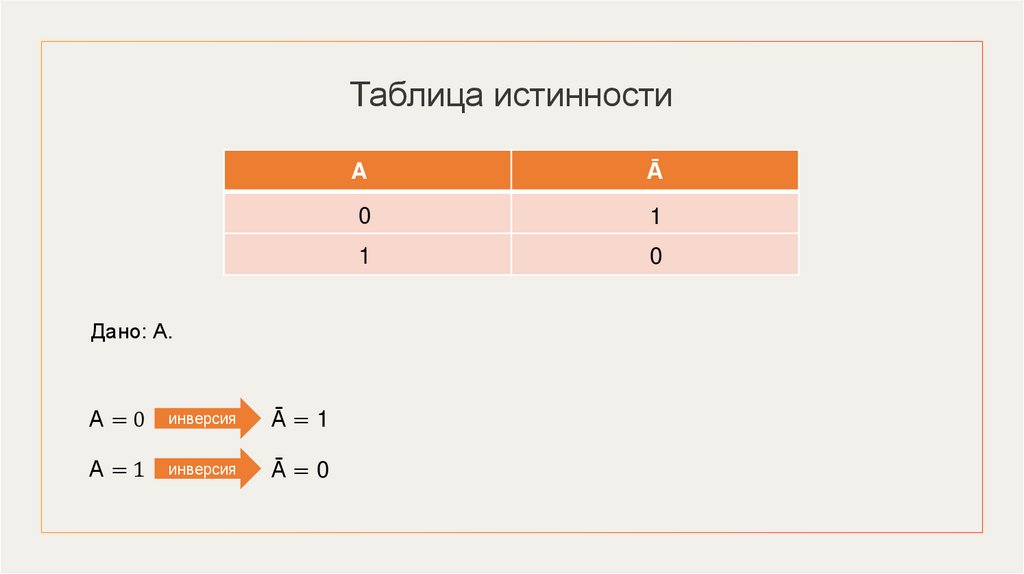
Таблица истинностиДано: А.
А=0
инверсия
Ā=1
А=1
инверсия
Ā=0
A
Ā
0
1
1
0
30.
Таблица истинностиA
Ā
0
1
1
0
Инверсия − логическое отрицание.
При применении к высказыванию логического отрицания в него добавляется
речевой оборот «неверно, что» или же частица «не».
Частица «не» прибавляется к глаголу.
31.
Сложные высказыванияЛогическое выражение
− это выражение, которое содержит переменные, знаки
логических операций и скобки.
А V В /\ A
(А V В) V B
Ā V (В /\ А)
АVВ
Ā /\ В
Порядок действий в логическом выражении:
1.
Инверсия.
2.
Конъюнкция.
3.
Дизъюнкция.
НЕ
1.
Отрицание (число меняется на противоположное).
2.
Конъюнкция (умножение).
+
3.
Дизъюнкция (сложение).
Порядок выполнения действий можно изменять с помощью скобок.
32.
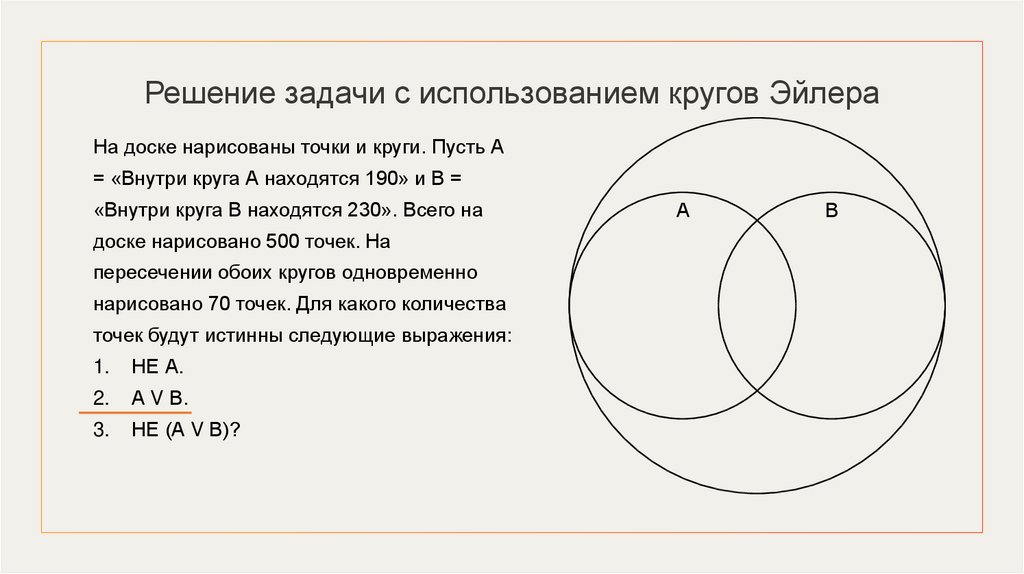
ПримерНа доске нарисованы точки и круги. Пусть А = «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на доске нарисовано 500 точек. На пересечении
обоих кругов одновременно нарисовано 70 точек. Для какого количества точек будут
истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
33.
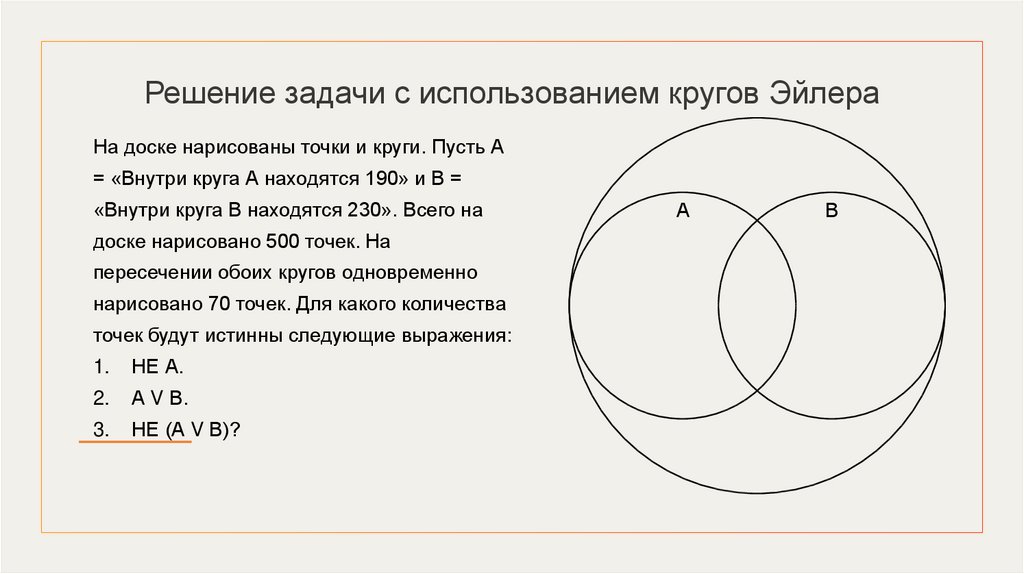
ПримерНа доске нарисованы точки и круги. Пусть А = «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на доске нарисовано 500 точек. На пересечении
обоих кругов одновременно нарисовано 70 точек. Для какого количества точек будут
истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А = «Внутри круга А находятся 190 точек».
Для 190 точек.
В = «Внутри круга В находятся 230 точек».
Для 230 точек.
34.
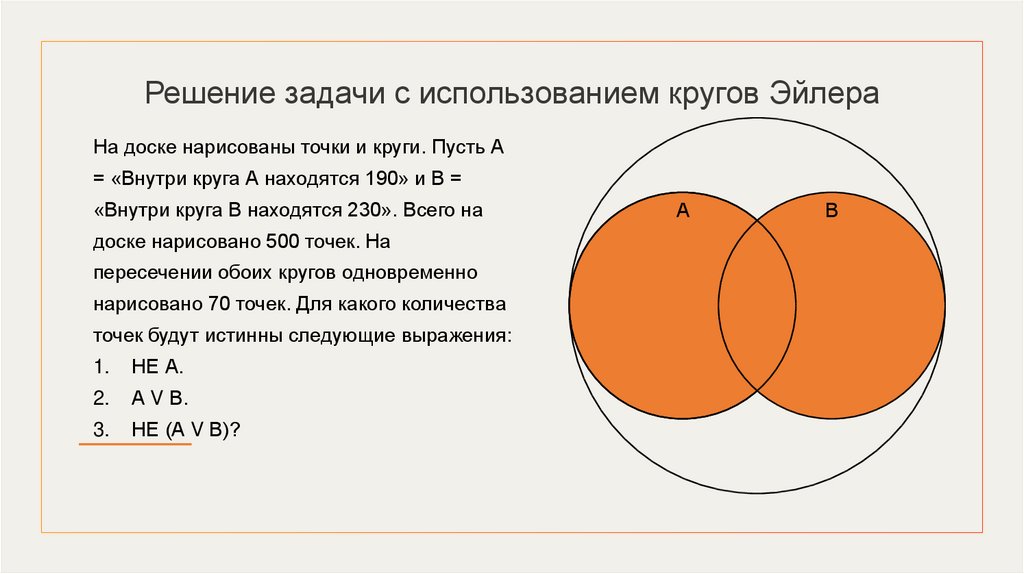
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А
В
35.
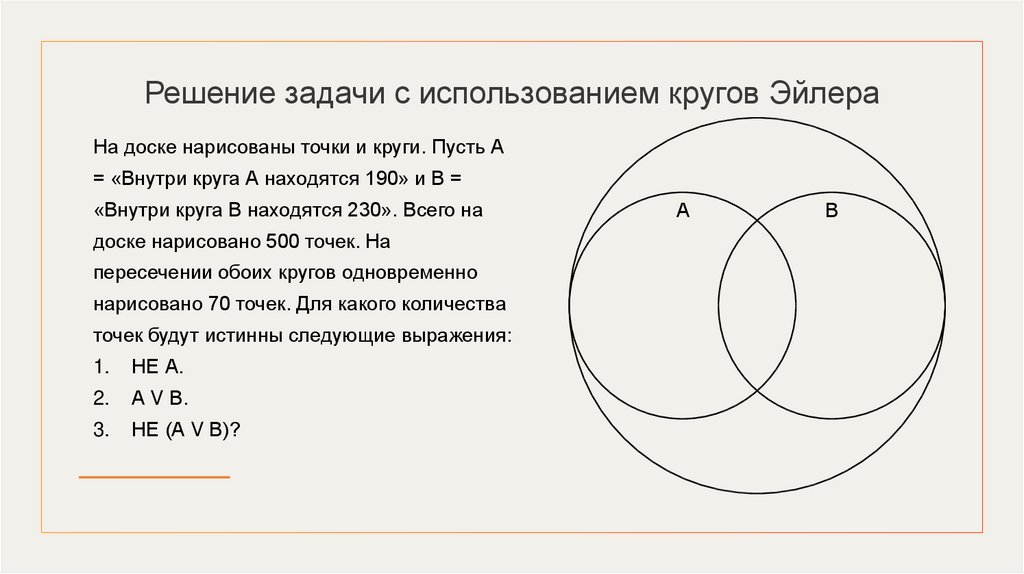
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А
В
36.
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А
В
37.
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А
В
38.
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А
В
39.
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
А
В
40.
Решение задачи с использованием кругов ЭйлераНа доске нарисованы точки и круги. Пусть А
1.
= «Внутри круга А находятся 190» и В =
«Внутри круга В находятся 230». Всего на
доске нарисовано 500 точек. На
2.
пересечении обоих кругов одновременно
нарисовано 70 точек. Для какого количества
точек будут истинны следующие выражения:
1.
НЕ А.
2.
А V В.
3.
НЕ (А V В)?
3.
41.
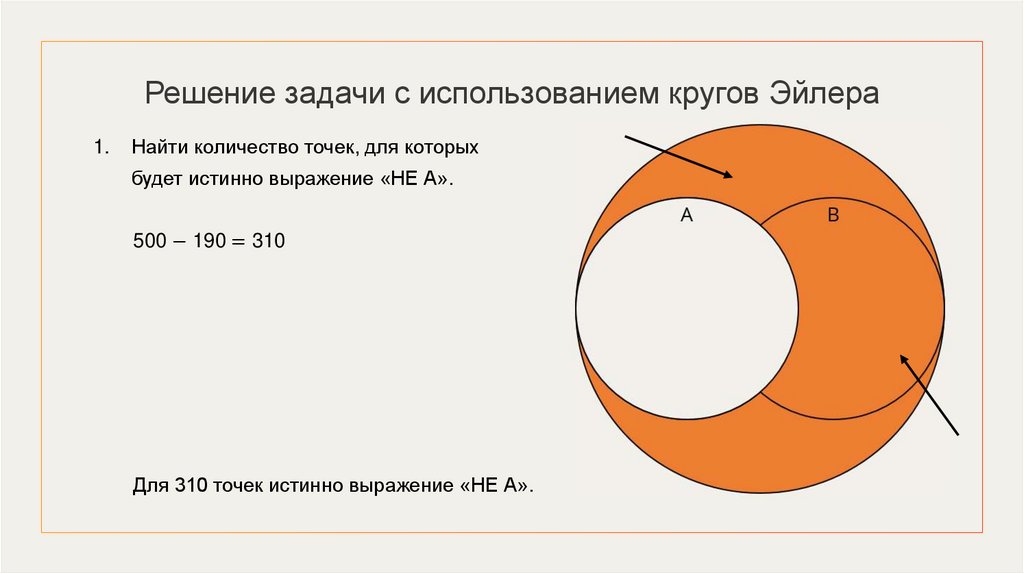
Решение задачи с использованием кругов Эйлера1.
Найти количество точек, для которых
будет истинно выражение «НЕ А».
500 − 190 = 310
Для 310 точек истинно выражение «НЕ А».
42.
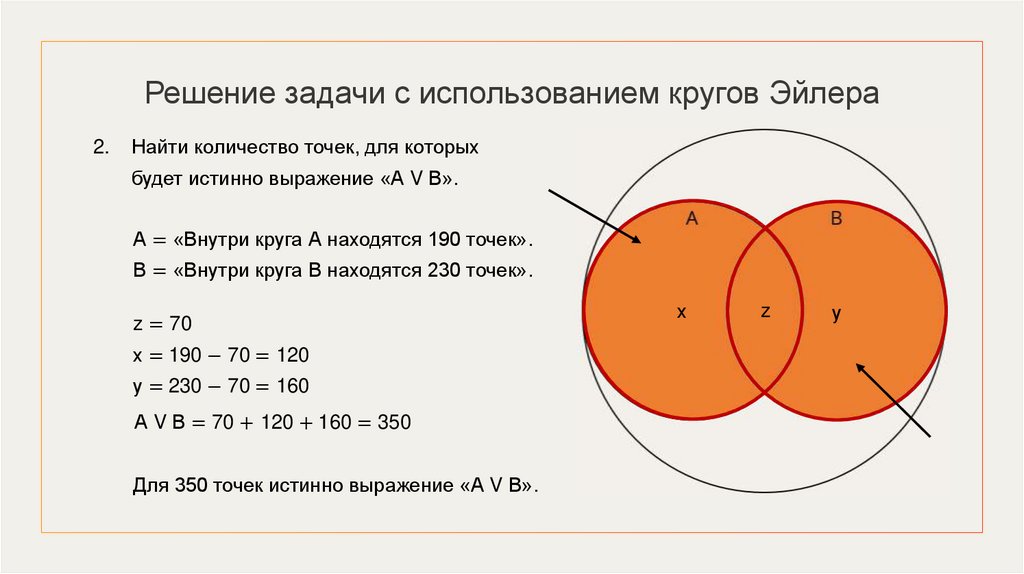
Решение задачи с использованием кругов Эйлера2.
Найти количество точек, для которых
будет истинно выражение «А V В».
А = «Внутри круга А находятся 190 точек».
В = «Внутри круга В находятся 230 точек».
z = 70
х = 190 − 70 = 120
у = 230 − 70 = 160
А V В = 70 + 120 + 160 = 350
Для 350 точек истинно выражение «А V В».
х
z
у
43.
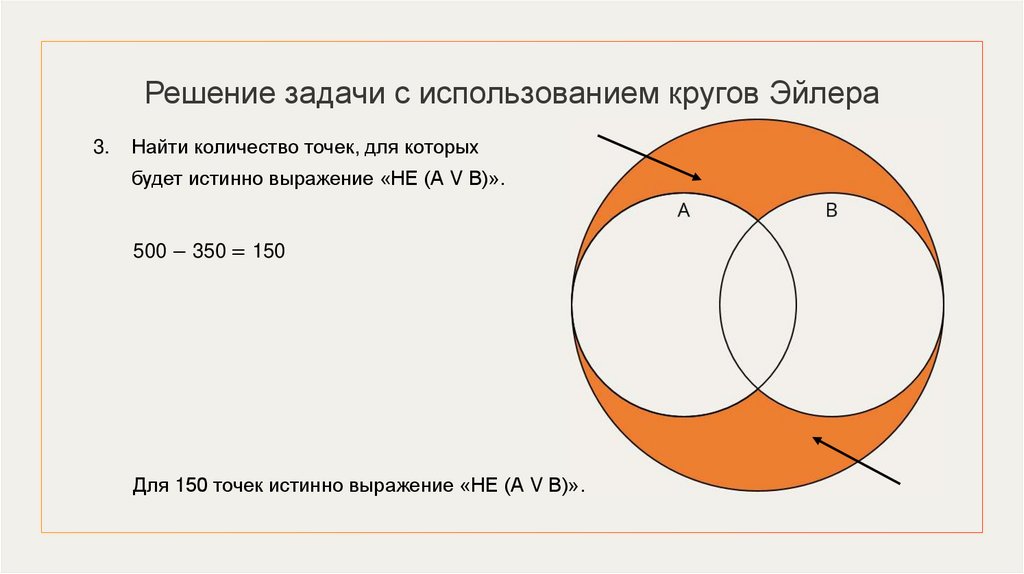
Решение задачи с использованием кругов Эйлера3.
Найти количество точек, для которых
будет истинно выражение «НЕ (А V В)».
500 − 350 = 150
Для 150 точек истинно выражение «НЕ (А V В)».
44.
Элементы алгебры логики. Логические операцииСложные высказывания — это высказывания, которые составляются из простых с
помощью логических операций.
Конъюнкция — это логическая операция, которая объединяет два высказывания в одно
новое, которое будет являться истинным тогда и только тогда, когда оба исходных
высказывания истинны.
Дизъюнкция — это логическая операция, которая объединяет два высказывания в одно
новое, которое будет являться ложным тогда и только тогда, когда оба исходных
высказывания ложны.
Инверсия — это логическая операция, которая преобразует исходное высказывание в
новое, значение которого противоположно исходному.
45.
Элементы алгебры логики. Логические операцииКонъюнкция −
логическое умножение.
Дизъюнкция −
логическое сложение.
Инверсия −
логическое отрицание.
46.
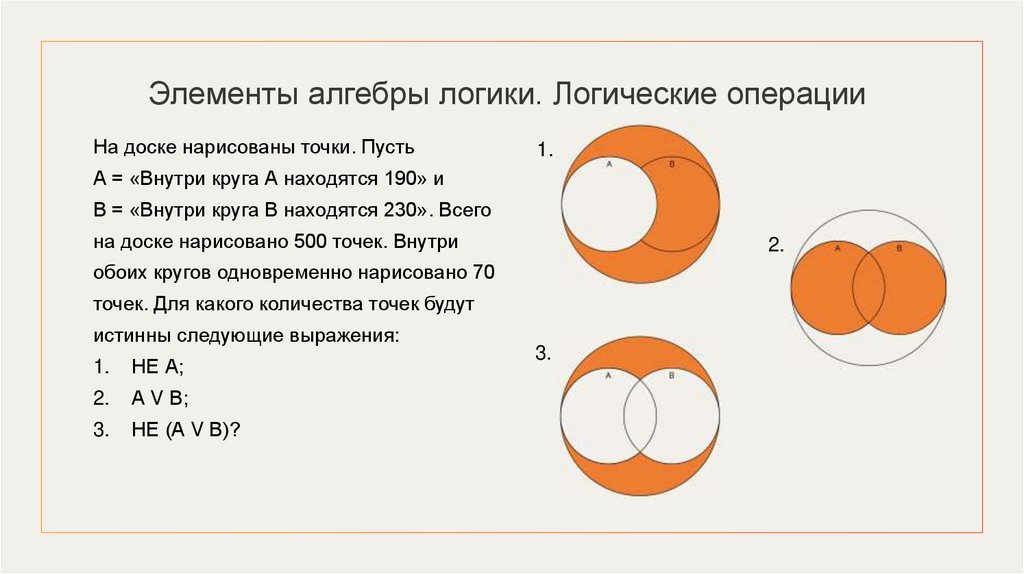
Элементы алгебры логики. Логические операцииНа доске нарисованы точки. Пусть
1.
А = «Внутри круга А находятся 190» и
В = «Внутри круга В находятся 230». Всего
на доске нарисовано 500 точек. Внутри
2.
обоих кругов одновременно нарисовано 70
точек. Для какого количества точек будут
истинны следующие выражения:
1.
НЕ А;
2.
А V В;
3.
НЕ (А V В)?
3.



















 informatics
informatics