Similar presentations:
Магнитное поле в веществе. (Лекция 17)
1.
МАГНИТНОЕ ПОЛЕ ВВЕЩЕСТВЕ
2.
Классификация магнетиков. Магнитные свойства атомов.Динамометр
Магнетик
Соленоид
Край
соленоида
Неоднородное поле
B
1.Относительно слабое
втягивание
ПАРАМАГНЕТИКИ
Al , Pt , Na, CuCl2 , O2 ....
2.Относительно слабое
выталкивание…
ДИАМАГНЕТИКИ
Cu , Ag , Bi, C , H 2O, N 2 ....
3. Сильное втягивание…
ФЕРРОМАГНЕТИКИ
Fe, Co, Ni....
3.
Магнитные свойства вещества связаны с магнитными свойствами атомов:Магнитный
момент атома
Магнитный момент,
связанный с орбитальным
движением электрона
éZ r
r
r ù r
pm = ê å ( poi + psiя) ú + p
ëi =1
û
Собственный магнитный
момент электрона имеет
квантовую природу и
является такими же
неотъемлемым его
свойством, как масса и
заряд.
Магнитный
момент ядра
4.
Магнитныймомент атома
éZ r
r
r ù r
pm = ê å ( poi + psiя) ú + p
ëi =1
û
Z r
r
r
pm » å ( poi + psi )
i =1
r
pm ¹ 0
для атома (молекулы)
парамагнетика
r
pm = 0
для атома (молекулы)
диамагнетиков
В ферромагнетиках
существуют области
спонтанного намагничивания:
«домены», магнитный момент
которых отличен от нуля.
r
pдомена ¹ 0
5.
Собственный магнитный момент атома. Гиромагнитное отношениеЭлектрон имеет собственный момент импульса
Собственный магнитный момент электрона
pS
r
Ls
– «спин».
.
pS = S LS
e
S = = 2
m
Орбитальные моменты pO и LO могут различаться для разных
электронов атома
Собственные моменты p S и LS одинаковы у всех электронов
Гиромагнитное
отношение для
спина
Например, они одинаковы у свободного электрона и у связанного
электрона в атоме.
6.
В атоме (молекуле) векторная сумма орбитальных и собственных магнитныхмоментов электронов равна полному магнитному моменту атома (молекулы).
Вследствие этого атомы (молекулы) можно рассматривать как микроскопические
круговые контура с током, получившие в физике название молекулярных токов
Ампера.
Как показывает опыт, для парамагнетиков и ферромагнетиков суммарный
магнитный момент атомов (молекул) отличен от нуля. Для диамагнетиков при
отсутствии магнитного поля он равен нулю.
7.
Характеристики магнитного поля в магнетиках.Число атомов
Вектор намагничивания
А/м
Магнитный
момент атома
Малый объём
(
B » const )
B0 - м.индукция, создаваемая макроскопическими токами
B - м.индукция, создаваемая «молекулярными токами» (токами Ампера)
Пара- и
B = B0 + B - полная м.индукция в магнетике B B0 ферромагнетики
B B0 диамагнетики
Введём напряжённость магнитного поля H
B
H=
J
0
Система СИ: размерность A/м (как и для J)
В вакууме:
B
H=
0
1 А/м
4π∙10-7 Тл
В не слишком сильных внешних полях (создаваемыми обычными токами)
не зависит от Н безразмерная величина
J = H
- магнитная восприимчивость (аналог диэлектрической восприимчивости)
8.
BH=
J
0
J = H
1+
B
H=
0 (1 + )
Характеристики магнитного
поля в магнетиках.
- магнитная проницаемость (аналог диэлектрической проницаемости)
μ - постоянный (при небольших полях) безразмерный коэффициент,
возможно μ ≥ 1 и μ ≤ 1)
B
H=
0
Простая связь между H и B
Очевидно, что B и
J должны быть связаны прямой пропорциональностью
Можно показать (Савельев т. 2), что B = 0 J
B
B
B
B = 0 J
)=
B = B0 + 0 J = B0 + 0 ( H ) = B0 + 0 (
0 0
0
B
B
H=
J
= B0 + B
0
B = B0
B
Напряжённость магнитного поля в
B
B0
H=
H=
=
= H 0 вакууме и магнетике одна и та же.
0
0 0
B = B0 + B
9.
Характеристики магнитного поля в магнетиках.B = B0
B
H=
0
B0
H=
= H0
0
Магнитная проницаемость
показывает во сколько раз
магнетик усиливает
(ослабляет) магнитное поле.
B ↔ Тесла (Тл)
Н ↔ А/м
r
B
= r
B0
Вакуум: поле создаётся только макроскопическими токами
B
= 0, = 1, B = B0 , H 0 = 0
0
B dl = å I
l
0
макро
H dl = å I
l
макро
Магнетик: поле создаётся макроскопическими и молекулярными
(Ампера) токами
B
¹ 0, ¹ 1, B = B0 , H = H 0 = 0
0
B dl = å I
l
0
макро
H dl = å I
l
макро
10.
Диамагнетикиr
r
B0 = 0 Þ pm = 0
r
r
¹0
B0 ¹ 0 Þ pm
Индуцированный
магнитный момент
атома
Если имеется контур, по которому может течь ток и включается магнитное поле, то,
согласно закону Фарадея, в контуре индуцируется ЭДС и порождаемый ею ток,
направленный так, чтобы ослабить внешнее магнитное поле (принцип Ленца).
Если считать, что электрон, движущийся по своей орбите в атоме – это контур с
током, то включение магнитного поля должно изменить движение электрона так,
чтобы возник дополнительный ток, уменьшающий внешнее магнитное поле.
Следует ожидать возникновения диамагнетизма.
Действительно, диамагнетизм возникает всегда, в том числе в пара- и
ферромагнетиках.
Но в пара- и ферромагнетиках диамагнитное ослабление внешнего магнитного
поля незаметно на фоне гораздо более сильных эффектов пара- и
ферромагнитного усиления поля.
11.
Рассмотрим орбитальное движение электрона в магнитном поле:r
B0
r
po
B0 r
стремящийся установить po
Контур с током в поле
вращательный
момент,
r
по
B0
r Закон изменения момента импульса:
M
Работа силы Лоренца равна нулю
a
r
r e
Контур с током
Орбитальное движение электрона
r
r
L0 = const.
r
L0
I
r
u
меняется только по
направлению !
r
r
p
Концы векторов Lи
0
0 движутся по
r
Lo
окружностям в плоскостях, перпендикулярных
линиям магнитной индукции с угловой
скоростью w L .
Прецессия векторов
r
r
po и L0
вокруг вектора
r
B0
12.
L2L1
B
wл
АТОМ
При включении магнитного поля атом (образованный
электронными орбитами) приобретает вращение вокруг
направления B с угловой скоростью ωл. При этом
наклонённые электронные орбиты прецессируют. Это
вроде соответствует описанию Сивухина.
13.
14.
15.
rB0
r
po
r
M
a
Траектория конца вектора L -
окружность в плоскости L и B
dL L и B
За время dt поворот на dφ
I
r
dL0
r
u
dφ
r
Lo
wЛ =
dj
= B0
dt
Частота
ларморовской
прецессии
wл
e
=
2m
e
wл =
B0
2m
одна и та же для всех орбит электронов в
атомах
16.
Сложное движение электронаr
B0
r
po
по круговой орбите радиуса r вокруг ядра
+ по окружности радиуса r’ в плоскости,
перпендикулярной линиям магнитной индукции.
r
B0
Можно трактовать, как
I
индуцированный (наведенный) ток.
r'
a
I
r
p
r
u
r
Lo
e2 2
=
r ' B0
4m
Индуцированный
орбитальный
магнитный момент
wл =
e
B0
2m
Направление индуцированного тока противоположно
направлению движения электрона
r
r
p ¯ B0
17.
Диамагнетики - резюмеe2 2
=
r ' B0
4m
Z
r
r
p m = å p i
i =1
Полный индуцированный магнитный момент для атома с числом
электронов Z
Z
r
r
r
r
p m = å ( poi + psi ) + p m
i =1
В диамагнетике
Индуцированный магнитный момент для
одного электрона в атоме.
Полный магнитный момент для атома с числом
электронов Z
r
r
å ( poi + psi ) = 0
Z
i =1
Магнитный момент атома определяется только величиной индуцированного магнитного
момента , имеющего направление противоположное направлению вектора магнитной
индукции.
Магнитный момент единицы
объёма диамагнетика
(вектор намагничивания) в
магнитном поле:
r
1
J =
DV
N
r
å pmj ¹ 0
j =1
r
r
J ¯ B0
18.
rB0
r
B0
I
r
J r
B
Диамагнетики - резюме
r r
r
B = B0 + B
B = B0 B '
Диамагнетики ослабляют
магнитное поле
B B0
Слабый эффект:
для твёрдых веществ χ имеет масштаб
10-6, μ ≈ 1
19.
rpm ¹ 0
Парамагнетики
Число атомов
Вектор намагничивания
r
pm
r
pm
А/м
Малый объём
(
B0
r
pm
r
pm
Магнитный
момент атома
B » const )
r
Ориентация магнитных моментов
B0 = 0
атомов носит случайный характер
J =0
B0 ¹ 0
M = [ pm B0 )
Тепло разупорядочивает
Магнитное поле выстраивает магнитные
моменты атомов вдоль линий магнитной
индукции
J ¹0
20.
rpm
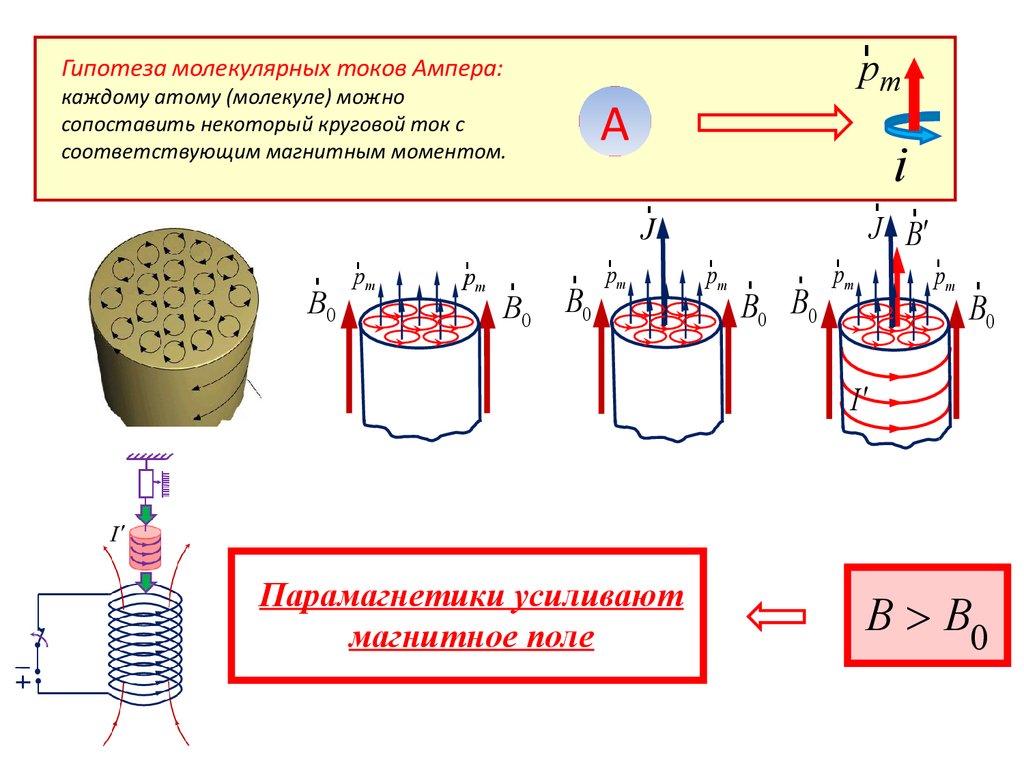
Гипотеза молекулярных токов Ампера:
каждому атому (молекуле) можно
сопоставить некоторый круговой ток с
соответствующим магнитным моментом.
r
B0
r
pm
r
pm
r
B0
А
r
B0
r
pm
r
J
i
r
pm
r r
B0 B0
r r
J B
r
pm
r
pm
r
B0
I
Парамагнетики усиливают
магнитное поле
B B0



















 physics
physics








