Two-Level Logic Minimization Algorithms. Lecture 3

1. Lecture 3 Two-Level Logic Minimization Algorithms

Hai Zhou
ECE 303
Advanced Digital Design
Spring 2002
ECE C03 Lecture 3
1

2. Outline

CAD Tools for 2-level minimization
Quine-McCluskey Method
ESPRESSO Algorithm
READING: Katz 2.4.1, 2.4.2, Dewey 4.5
ECE C03 Lecture 3
2

3. Two-Level Simplification Approaches

Algebraic Simplification:
not an algorithm/systematic procedure
how do you know when the minimum realization has been found?
Computer-Aided Tools:
precise solutions require very long computation times,
especially for functions with many inputs (>10)
heuristic methods employed —
"educated guesses" to reduce the amount of computation
good solutions not best solutions
Still Relevant to Learn Hand Methods:
insights into how the CAD programs work, and their
strengths and weaknesses
ability to check the results, at least on small examples
ECE C03 Lecture 3
3

4. Review of Karnaugh Map Method

Algorithm: Minimum Sum of Products Expression from a K-Map
Step 1:
Choose an element of ON-set not already covered by an implicant
Step 2:
Find "maximal" groupings of 1's and X's adjacent to that element.
Remember to consider top/bottom row, left/right column, and
corner adjacencies. This forms prime implicants (always a power
of 2 number of elements).
Repeat Steps 1 and 2 to find all prime implicants
Step 3:
Revisit the 1's elements in the K-map. If covered by single prime
implicant, it is essential, and participates in final cover. The 1's it
covers do not need to be revisited
Step 4:
If there remain 1's not covered by essential prime implicants, then
select the smallest number of prime implicants that cover the
remaining 1's
ECE C03 Lecture 3
4

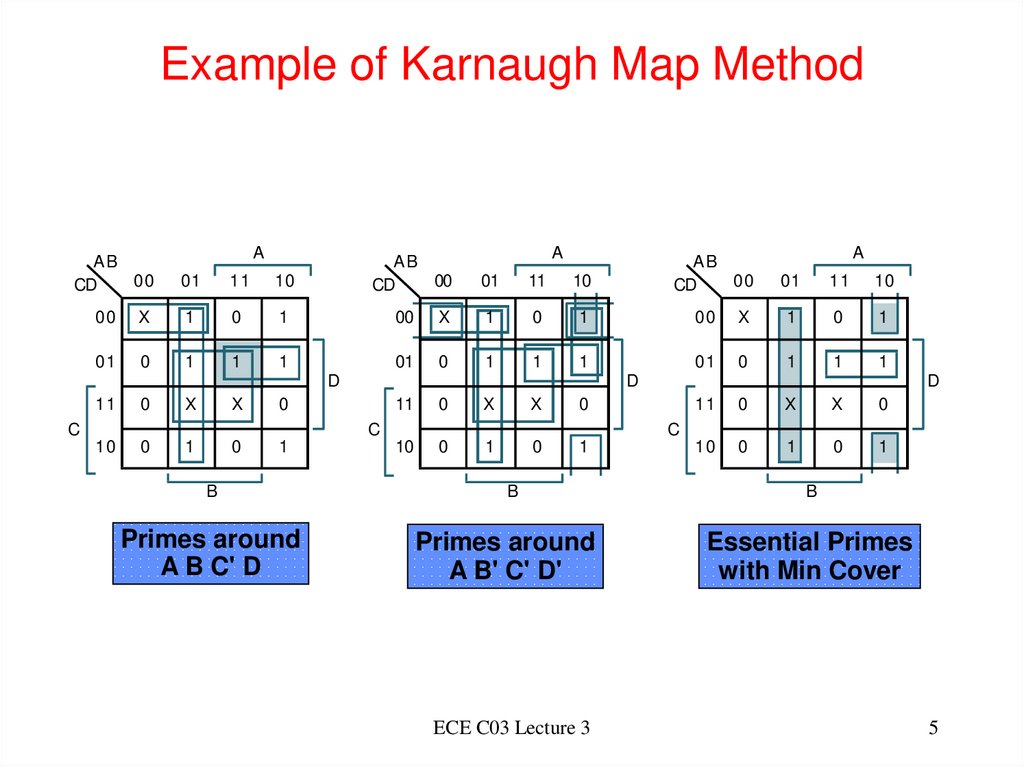
5. Example of Karnaugh Map Method

AB
00
CD
A
01
11
10
AB
00
CD
A
01
11
10
AB
00
CD
A
01
11
10
00
X
1
0
1
00
X
1
0
1
00
X
1
0
1
01
0
1
1
1
01
0
1
1
1
01
0
1
1
1
D
11
0
X
X
0
10
0
1
0
1
C
D
11
0
X
X
0
10
0
1
0
1
C
B
Primes around
A B C' D
D
11
0
X
X
0
10
0
1
0
1
C
B
Primes around
A B' C' D'
ECE C03 Lecture 3
B
Essential Primes
with Min Cover
5

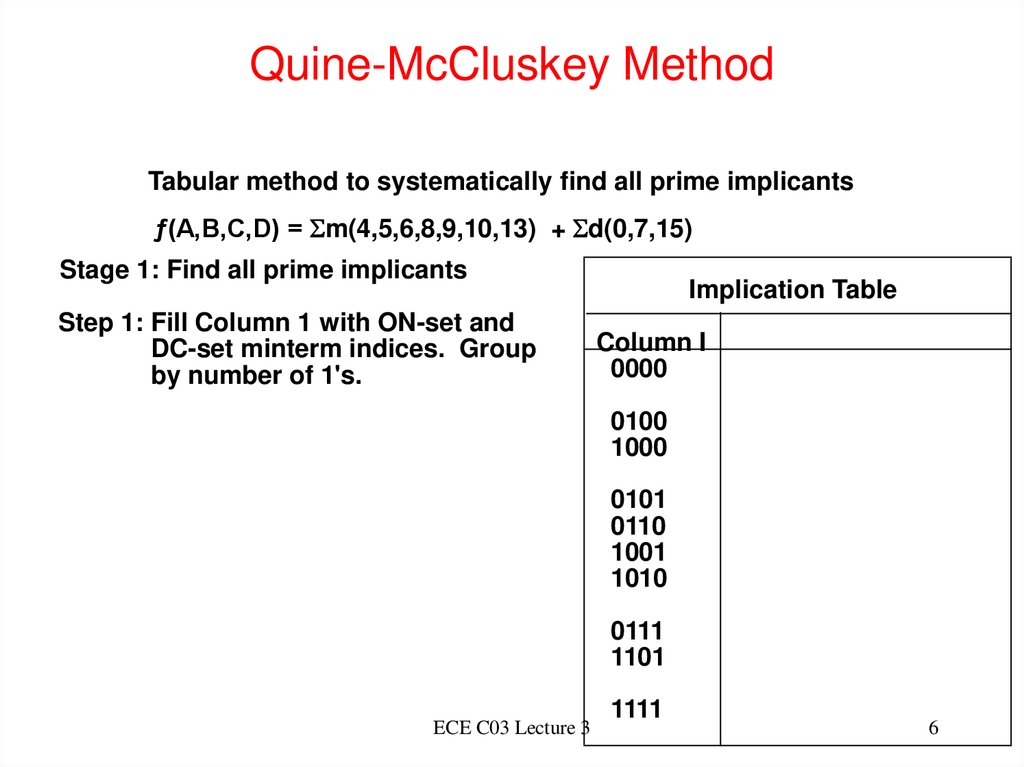
6. Quine-McCluskey Method

Tabular method to systematically find all prime implicants
ƒ(A,B,C,D) = Sm(4,5,6,8,9,10,13) + Sd(0,7,15)
Stage 1: Find all prime implicants
Step 1: Fill Column 1 with ON-set and
DC-set minterm indices. Group
by number of 1's.
Implication Table
Column I
0000
0100
1000
0101
0110
1001
1010
0111
1101
ECE C03 Lecture 3
1111
6

7. Quine-McCluskey Method

Tabular method to systematically find all prime implicants
ƒ(A,B,C,D) = S m(4,5,6,8,9,10,13) + S d(0,7,15)
Stage 1: Find all prime implicants
Step 1: Fill Column 1 with ON-set and
DC-set minterm indices. Group
by number of 1's.
Step 2: Apply Uniting Theorem—
Compare elements of group w/
N 1's against those with N+1 1's.
Differ by one bit implies adjacent.
Eliminate variable and place in
next column.
E.g., 0000 vs. 0100 yields 0-00
0000 vs. 1000 yields -000
Implication Table
Column I Column II
0000 ¦
0-00
-000
0100 ¦
1000 ¦
01001-0
0101 ¦
1000110 ¦
10-0
1001 ¦
1010 ¦
01-1
-101
0111 ¦
0111101 ¦
1-01
When used in a combination,
mark with a check. If cannot be
1111 ¦
-111
combined, mark with a star. These
11-1
are the prime implicants.
ECE C03 Lecture 3 can be made.
Repeat until no further combinations
7

8. Quine Mcluskey Method

Tabular method to systematically find all prime implicants
ƒ(A,B,C,D) = Sm(4,5,6,8,9,10,13) + Sd(0,7,15)
Stage 1: Find all prime implicants
Implication Table
Step 1: Fill Column 1 with ON-set and
DC-set minterm indices. Group
Column I Column II Column III
by number of 1's.
0000 ¦
0-00 *
01-- *
-000 *
Step 2: Apply Uniting Theorem—
0100 ¦
-1-1 *
Compare elements of group w/
1000 ¦
010- ¦
N 1's against those with N+1 1's.
01-0 ¦
Differ by one bit implies adjacent.
0101 ¦
100- *
Eliminate variable and place in
0110 ¦
10-0 *
next column.
1001 ¦
1010 ¦
01-1 ¦
E.g., 0000 vs. 0100 yields 0-00
-101 ¦
0000 vs. 1000 yields -000
0111 ¦
011- ¦
1101 ¦
1-01 *
When used in a combination,
mark with a check. If cannot be
1111 ¦
-111 ¦
combined, mark with a star. These
11-1 ¦
are the prime implicants.
Repeat until no further combinations
ECE C03 Lecture 3can be made.
8

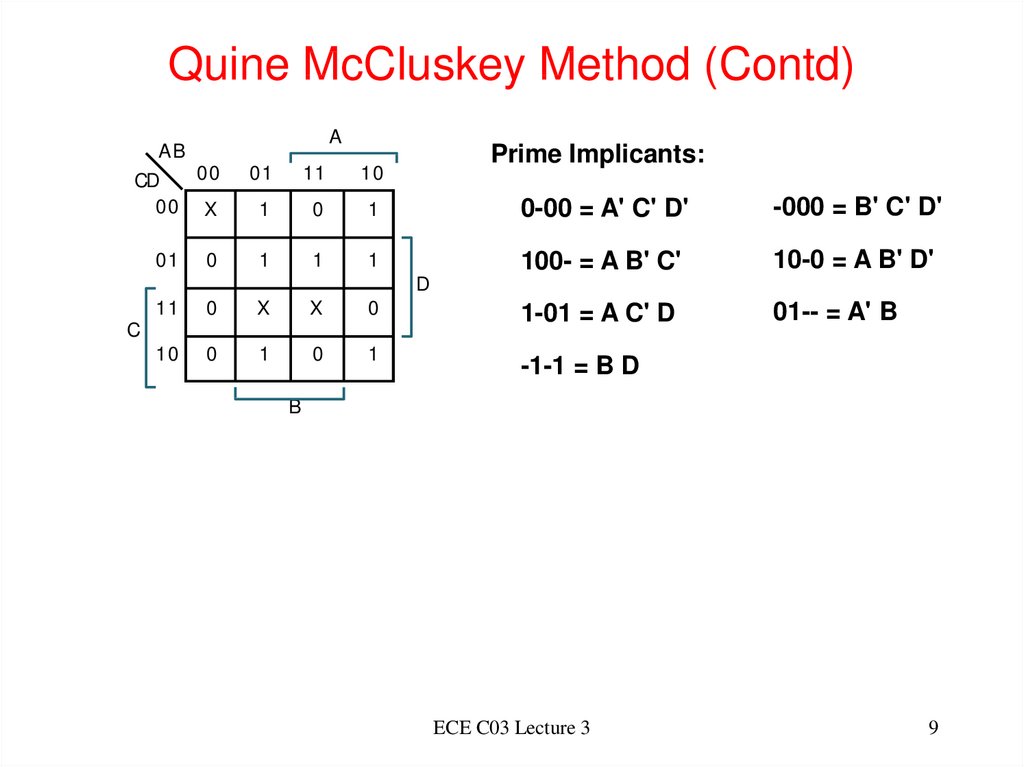
9. Quine McCluskey Method (Contd)

AB
00
CD
00 X
01
0
A
Prime Implicants:
01
11
10
1
0
1
0-00 = A' C' D'
-000 = B' C' D'
1
1
1
100- = A B' C'
10-0 = A B' D'
01-- = A' B
D
11
0
X
X
0
1-01 = A C' D
10
0
1
0
1
-1-1 = B D
C
B
ECE C03 Lecture 3
9

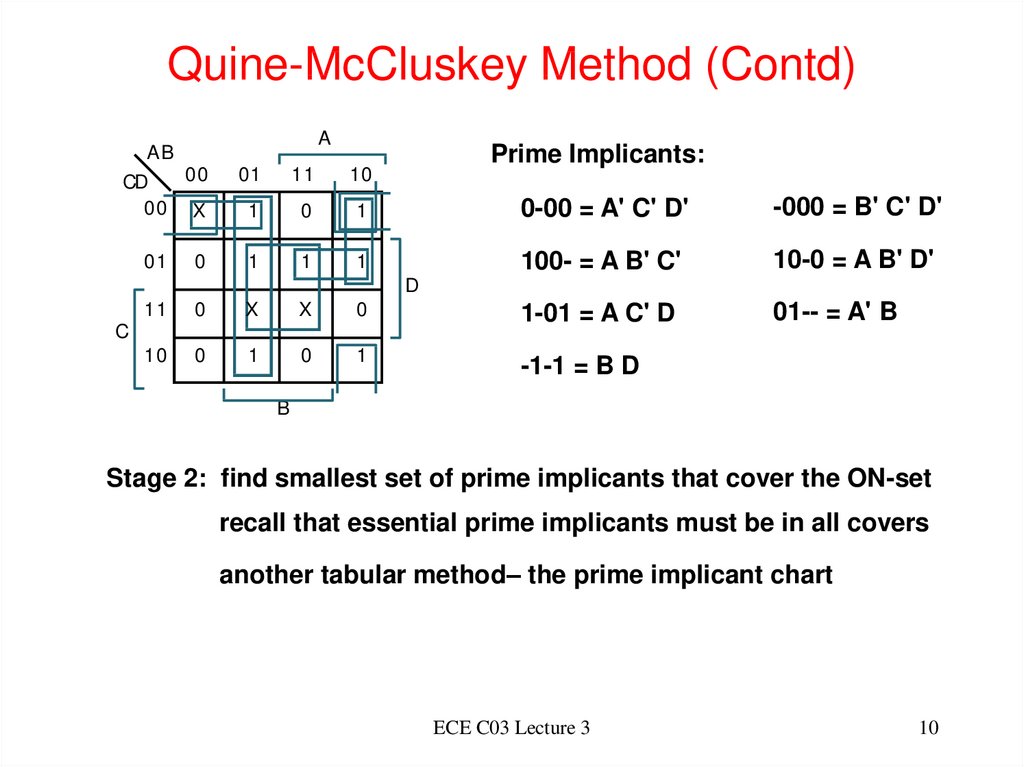
10. Quine-McCluskey Method (Contd)

AB
00
CD
00 X
01
0
A
Prime Implicants:
01
11
10
1
0
1
0-00 = A' C' D'
-000 = B' C' D'
1
1
1
100- = A B' C'
10-0 = A B' D'
01-- = A' B
D
11
0
X
X
0
1-01 = A C' D
10
0
1
0
1
-1-1 = B D
C
B
Stage 2: find smallest set of prime implicants that cover the ON-set
recall that essential prime implicants must be in all covers
another tabular method– the prime implicant chart
ECE C03 Lecture 3
10

11. Finding the Minimum Cover

• We have so far found all the prime implicants
• The second step of the Q-M procedure is to find
the smallest set of prime implicants to cover the
complete on-set of the function
• This is accomplished through the prime implicant
chart
– Columns are labeled with the minterm indices of the
onset
– Rows are labeled with the minterms covered by a given
prime implicant
– Example a prime implicant (-1-1) becomes minterms
0101, 0111, 1101, 1111, which are indices of minterms
m5, m7, m13, m15 ECE C03 Lecture 3
11

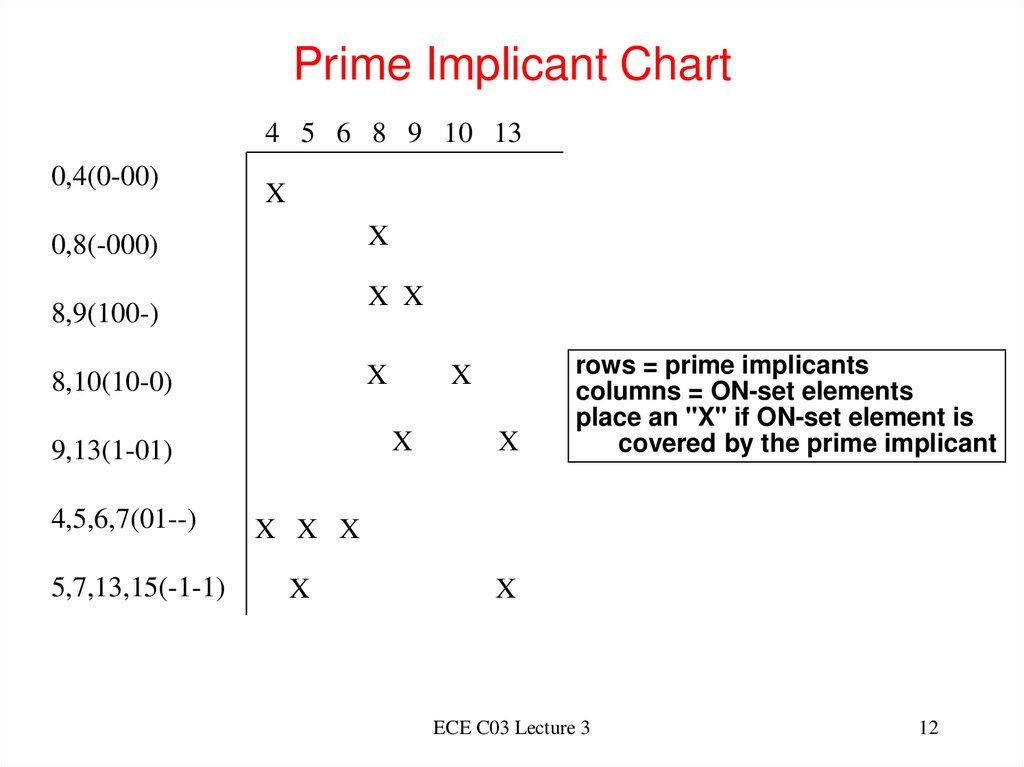
12. Prime Implicant Chart

4 5 6 8 9 10 13
0,4(0-00)
X
X
0,8(-000)
X X
8,9(100-)
X
8,10(10-0)
X
9,13(1-01)
4,5,6,7(01--)
5,7,13,15(-1-1)
X
X
rows = prime implicants
columns = ON-set elements
place an "X" if ON-set element is
covered by the prime implicant
X X X
X
X
ECE C03 Lecture 3
12

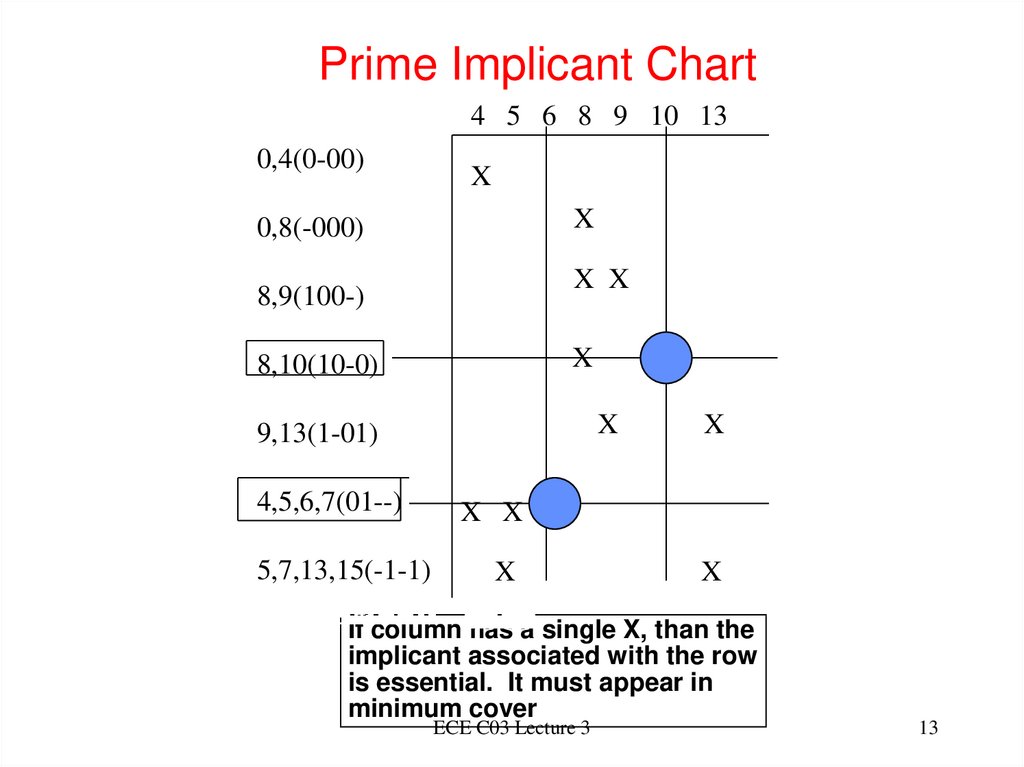
13. Prime Implicant Chart

4 5 6 8 9 10 13
0,4(0-00)
X
X
0,8(-000)
X X
8,9(100-)
X
8,10(10-0)
X
9,13(1-01)
4,5,6,7(01--)
5,7,13,15(-1-1)
X
X
X X X
X
X
If column has a single X, than the
implicant associated with the row
is essential. It must appear in
minimum cover
ECE C03 Lecture 3
13

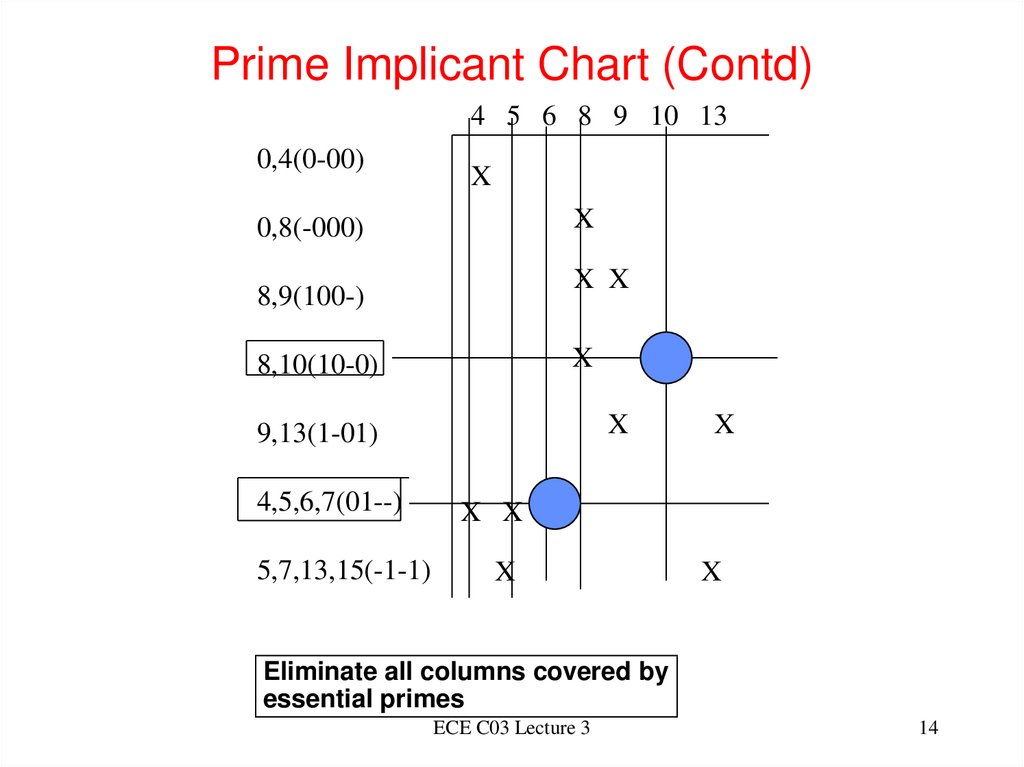
14. Prime Implicant Chart (Contd)

4 5 6 8 9 10 13
0,4(0-00)
X
X
0,8(-000)
X X
8,9(100-)
X
8,10(10-0)
X
9,13(1-01)
4,5,6,7(01--)
5,7,13,15(-1-1)
X
X
X X X
X
X
Eliminate all columns covered by
essential primes
ECE C03 Lecture 3
14

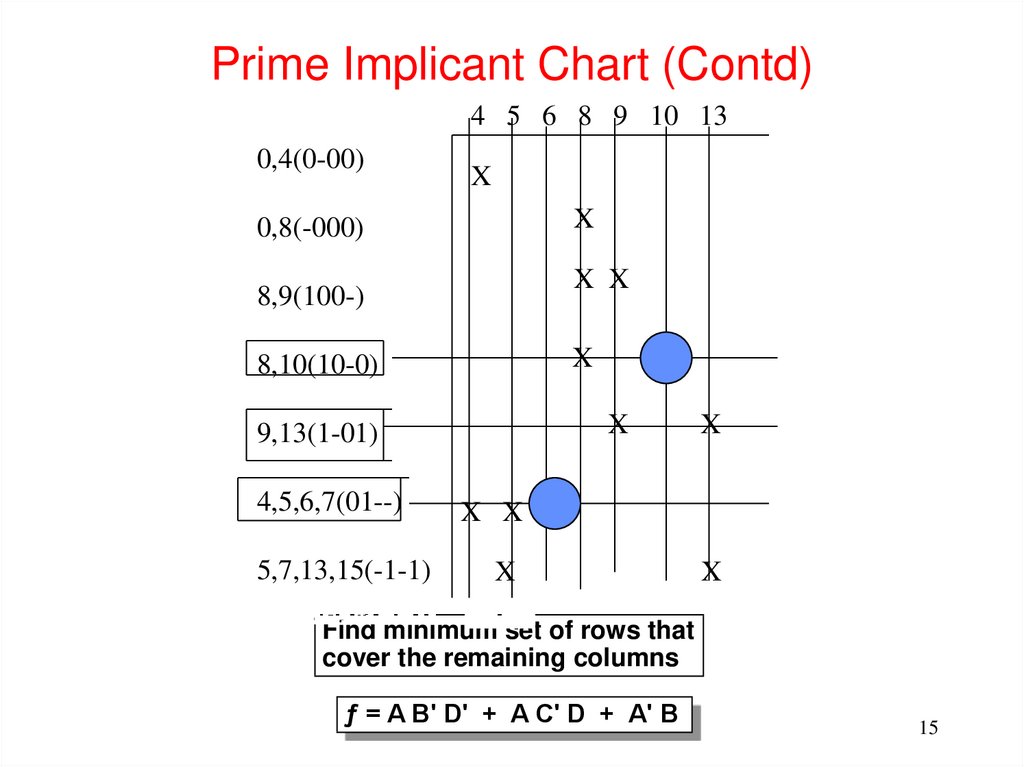
15. Prime Implicant Chart (Contd)

4 5 6 8 9 10 13
0,4(0-00)
X
X
0,8(-000)
X X
8,9(100-)
X
8,10(10-0)
X
9,13(1-01)
4,5,6,7(01--)
5,7,13,15(-1-1)
X
X
X X X
X
X
Find minimum set of rows that
cover the remaining columns
ƒ = A B'ECE
D' C03
+ A
C' D + A' B
Lecture 3
15

16. Second Example of Q-M Method

Assume function F(A,B,C,D) = S m(0, 1, 4, 5, 7, 12, 14, 15)
Implication Table
Enumerate the minterms in order
of number of uncomplemented variables
Column I lists them
minterms with 0 : 0
minterms with 1: 1,4
minterms with 2: 5,12
minterms with 3: 7,14
minterms with 4: 15
Column I Column II
0( 0000)
0,1
0,4
Column II combines minterms that are
adjacent in one variable
example, 0,1 and 0.4 , etc.
ECE C03 Lecture 3
1( 0001)
4( 0100)
1,5
4,5
4,12
5( 0101)
12(1100)
5,7
12,14
7( 0111)
14(1110)
7,15
14,15
15( 1111)
16

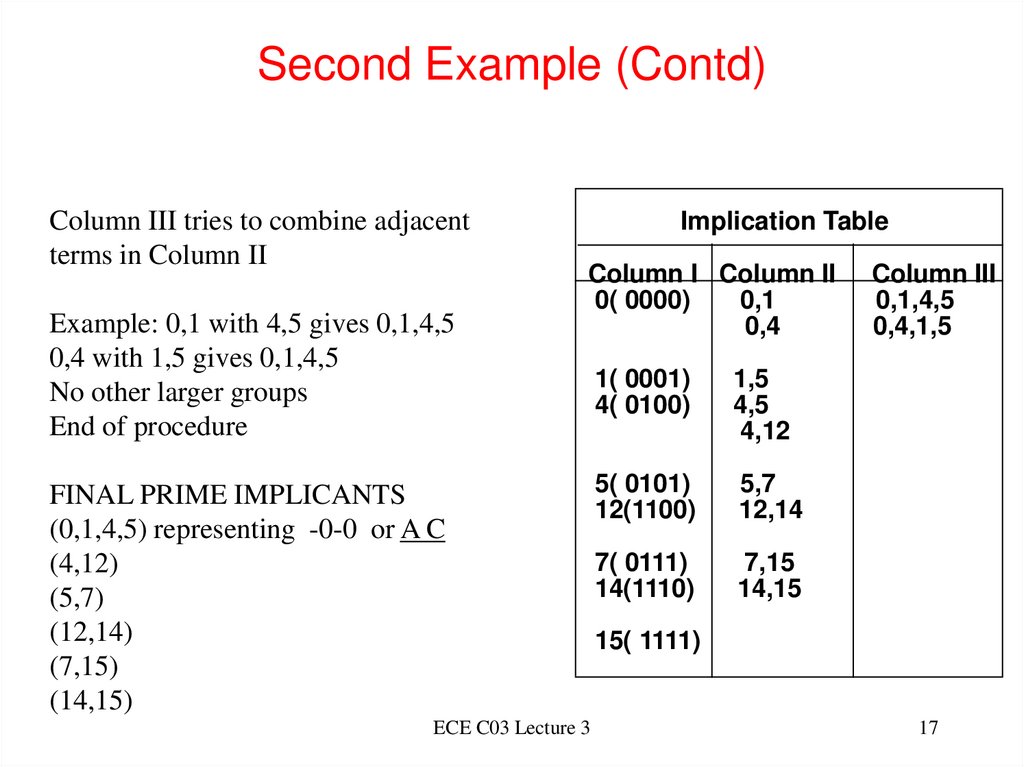
17. Second Example (Contd)

Column III tries to combine adjacent
terms in Column II
Example: 0,1 with 4,5 gives 0,1,4,5
0,4 with 1,5 gives 0,1,4,5
No other larger groups
End of procedure
Implication Table
Column I Column II
0( 0000)
0,1
0,4
FINAL PRIME IMPLICANTS
(0,1,4,5) representing -0-0 or A C
(4,12)
(5,7)
(12,14)
(7,15)
(14,15)
ECE C03 Lecture 3
1( 0001)
4( 0100)
1,5
4,5
4,12
5( 0101)
12(1100)
5,7
12,14
7( 0111)
14(1110)
7,15
14,15
Column III
0,1,4,5
0,4,1,5
15( 1111)
17

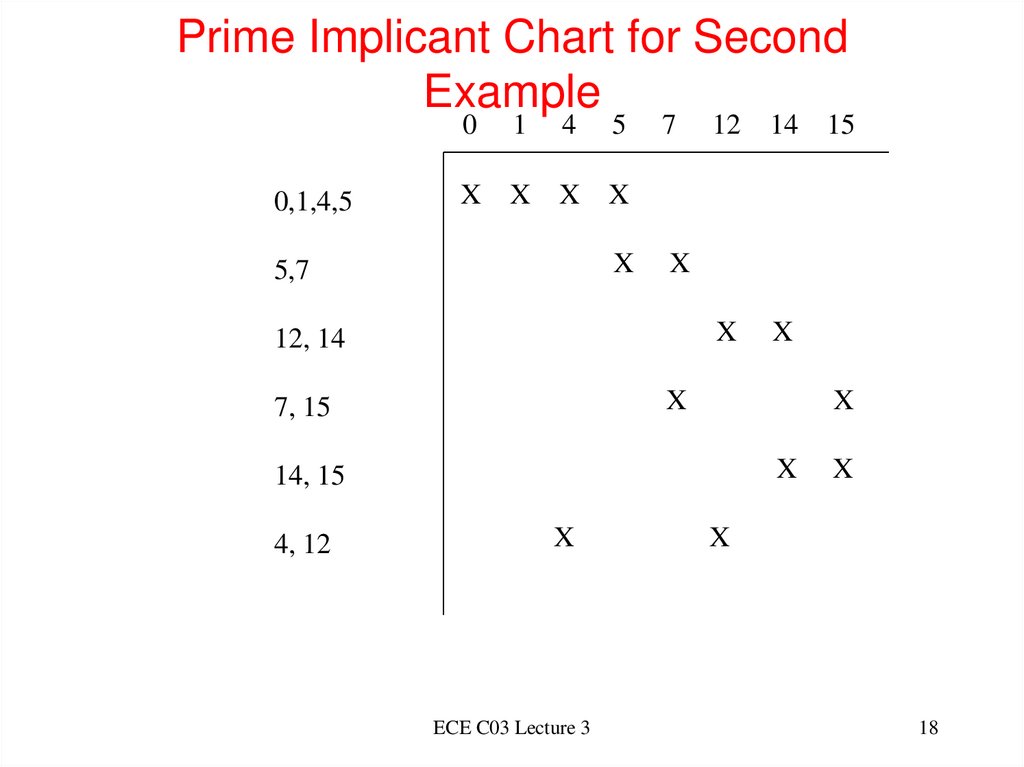
18. Prime Implicant Chart for Second Example

0
0,1,4,5
1
X X
4
5
7
12
14 15
X
X
X X
X
5,7
X
12, 14
X
7, 15
X
X
14, 15
4, 12
X
ECE C03 Lecture 3
X
X
18

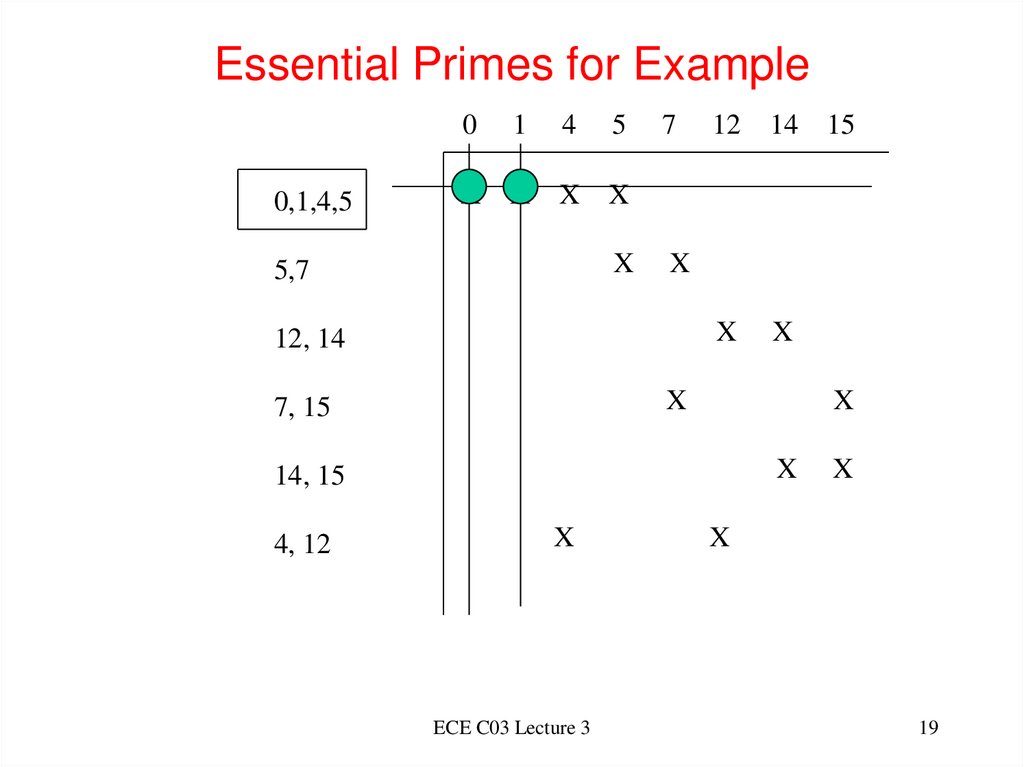
19. Essential Primes for Example

0
0,1,4,5
1
X X
4
5
7
12
14 15
X
X
X X
X
5,7
X
12, 14
X
7, 15
X
X
14, 15
4, 12
X
ECE C03 Lecture 3
X
X
19

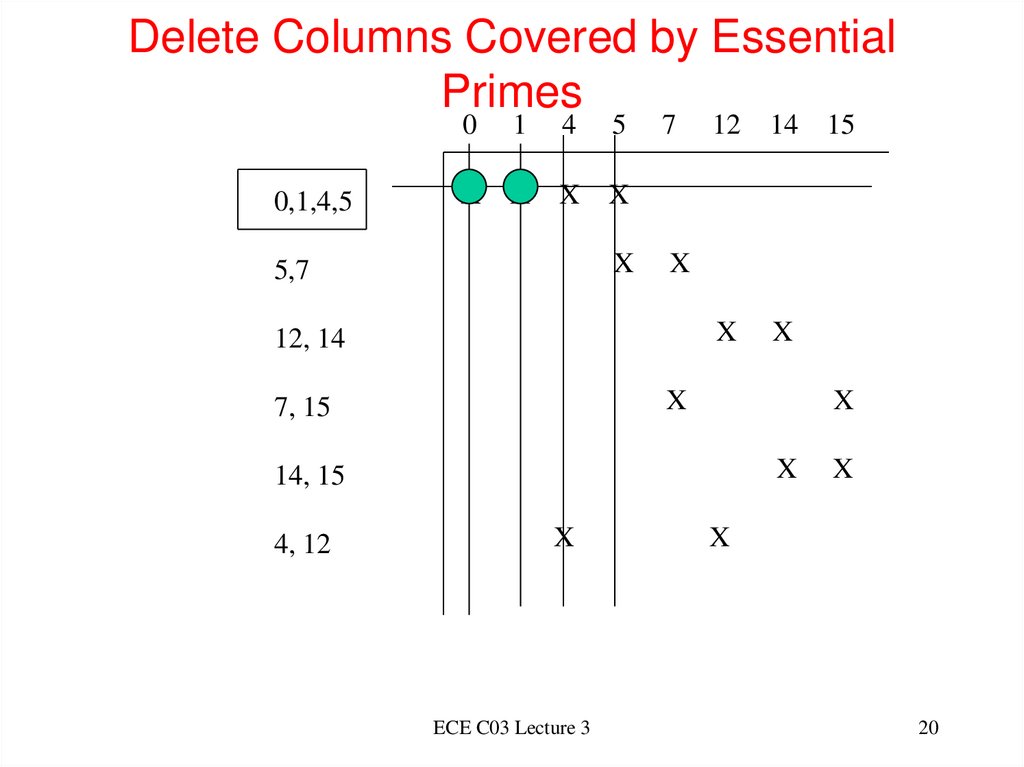
20. Delete Columns Covered by Essential Primes

0
0,1,4,5
1
X X
4
5
7
12
14 15
X
X
X X
X
5,7
X
12, 14
X
7, 15
X
X
14, 15
4, 12
X
ECE C03 Lecture 3
X
X
20

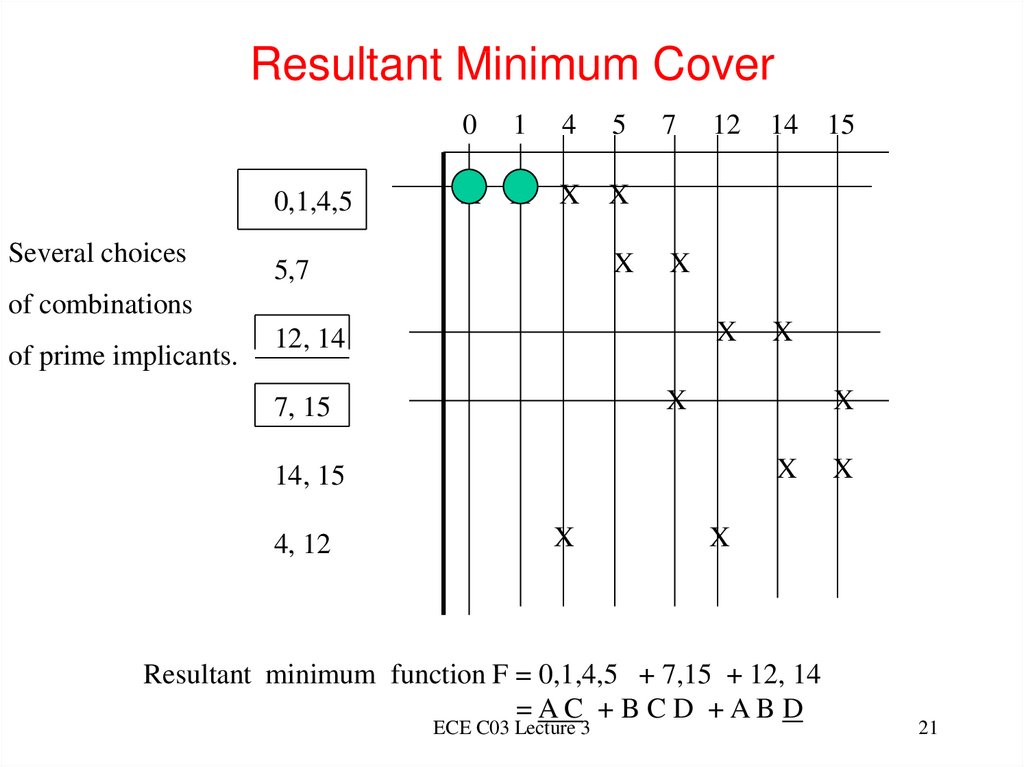
21. Resultant Minimum Cover

0
0,1,4,5
Several choices
1
X X
4
5
7
12
14 15
X
X
X X
X
5,7
X
of combinations
of prime implicants.
12, 14
X
7, 15
X
X
14, 15
4, 12
X
X
Resultant minimum function F = 0,1,4,5 + 7,15 + 12, 14
=AC + B C D +AB D
ECE C03 Lecture 3
X
21

22. ESPRESSO Method

Problem with Quine-McCluskey: the number of prime implicants
grows rapidly with the number of inputs
upper bound: 3 n /n, where n is the number of inputs
finding a minimum cover is NP-complete, i.e., a computational
expensive process not likely to yield to any efficient
algorithm
Espresso: trades solution speed for minimality of answer
don't generate all prime implicants (Quine-McCluskey Stage 1)
judiciously select a subset of primes that still covers the ON-set
operates in a fashion not unlike a human finding primes in a K-map
ECE C03 Lecture 3
22

23. Boolean Space

• The notion of redundancy can be formulated in
Boolean space
• Every point in a Boolean space corresponds to an
assignment of values (0 or 1) to variables.
• The on-set of a Boolean function is set of points
(shown in black) where function is 1 (similarly for
off-set and don’t--care set)001
011
101
111
Consider three Boolean
000
variables x1, x2, x3
010
100
ECE C03 Lecture 3
110
23

24. Boolean Space

• If g and h are two Boolean functions such that onset of g is a subset of on-set of h, then we write
– g C h
• Example g = x1 x2 x3 and h = x1 x2
• In general if f = p1 + p2 + ….pn, check if pi C
p1 + p2 + …p I-1 + pn
001
011
101
111
000
100
ECE C03 Lecture 3
010
110
24

25. Redundancy in Boolean Space

• x1 x2 is said to cover x1 x2 x3
• Thus redundancy can be identified by looking for
inclusion or covering in the Boolean space
• While redundancy is easy to observe by looking at
the product terms, it is not always the case
– If f = x2 x3 + x1 x2 + x1 x3, then x1 x2 is redundant
• Situation is more complicated with multiple output
functions
– f1 = p11 + p12 + … + p1n
– f2 = ….
– Fm = pm1 + pm2 + … p mn
ECE C03 Lecture 3
25

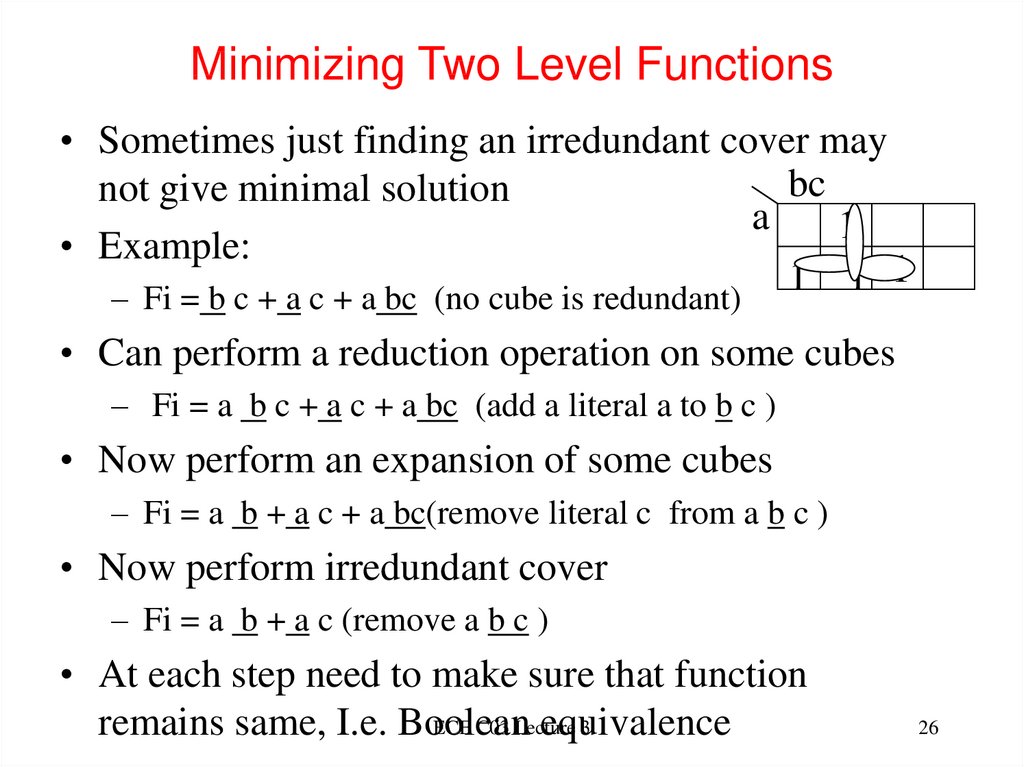
26. Minimizing Two Level Functions

• Sometimes just finding an irredundant cover may
bc
not give minimal solution
a
1
• Example:
1
1
1
– Fi = b c + a c + a bc (no cube is redundant)
• Can perform a reduction operation on some cubes
– Fi = a b c + a c + a bc (add a literal a to b c )
• Now perform an expansion of some cubes
– Fi = a b + a c + a bc(remove literal c from a b c )
• Now perform irredundant cover
– Fi = a b + a c (remove a b c )
• At each step need to make sure that function
ECE C03 Lecture
3
remains same, I.e. Boolean
equivalence
26

27. Espresso Algorithm

1. Expands implicants to their maximum size
Implicants covered by an expanded implicant are removed from
further consideration
Quality of result depends on order of implicant expansion
Heuristic methods used to determine order
Step is called EXPAND
2.
Irredundant cover (i.e., no proper subset is also a cover) is extracted
from the expanded primes
Just like the Quine-McCluskey Prime Implicant Chart
Step is called IRREDUNDANT COVER
3.
Solution usually pretty good, but sometimes can be improved
Might exist another cover with fewer terms or fewer literals
Shrink prime implicants to smallest size that still covers ON-set
Step is called REDUCE
4.
Repeat sequence REDUCE/EXPAND/IRREDUNDANT COVER to find
alternative prime implicants
Keep doing this as long as new covers improve on last solution
5.
A number of optimizations are tried, e.g., identify and remove
essential primes early in the process
ECE C03 Lecture 3
27

28. Details of ESPRESSO Algorithm

Procedure ESPRESSO ( F, D, R) /* F is ON set, D is don’t care, R OFF *
R = COMPLEMENT(F+D); /* Compute complement */
F = EXPAND(F, R) ; /* Initial expansion */
F = IRREDUNDANT(F,D); /* Initial irredundant cover */
F = ESSENTIAL(F,D) /* Detecting essential primes */
F = F - E; /* Remove essential primes from F */
D = D + E; /* Add essential primes to D */
WHILE Cost(F) keeps decreasing DO
F = REDUCE(F,D); /* Perform reduction, heuristic which cubes */
F = EXPAND(F,R); /* Perform expansion, heuristic which cubes */
F = IRREDUNDANT(F,D); /* Perform irredundant cover */
ENDWHILE;
F = F + E;
RETURN F;
END Procedure;
ECE C03 Lecture 3
28

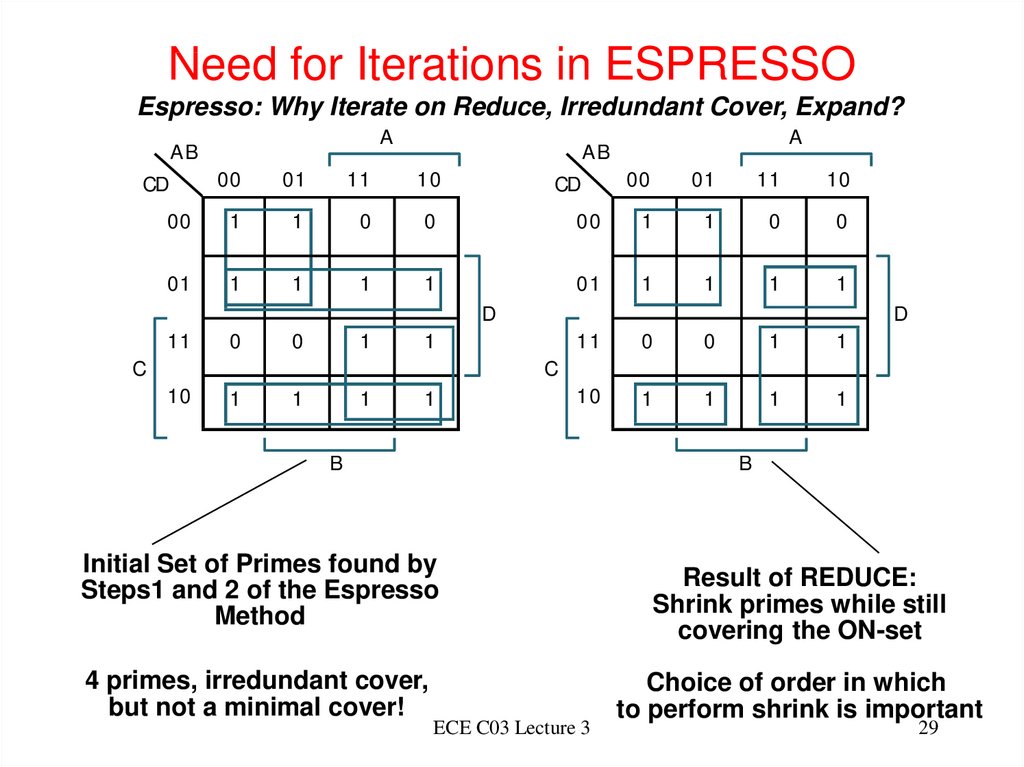
29. Need for Iterations in ESPRESSO

Espresso: Why Iterate on Reduce, Irredundant Cover, Expand?
A
AB
00
01
11
10
00
1
1
0
0
01
1
1
1
1
CD
A
AB
00
01
11
10
00
1
1
0
0
01
1
1
1
1
CD
D
11
0
0
1
D
1
C
11
0
0
1
1
10
1
1
1
1
C
10
1
1
1
1
B
B
Initial Set of Primes found by
Steps1 and 2 of the Espresso
Method
4 primes, irredundant cover,
but not a minimal cover!
ECE C03 Lecture 3
Result of REDUCE:
Shrink primes while still
covering the ON-set
Choice of order in which
to perform shrink is important
29

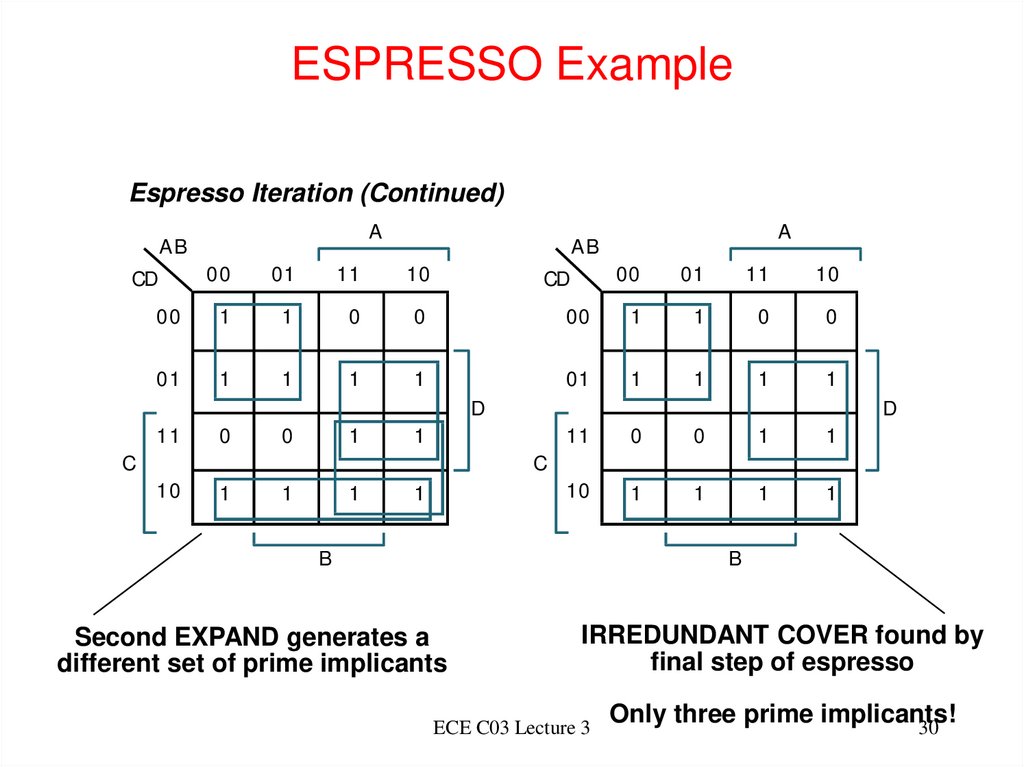
30. ESPRESSO Example

Espresso Iteration (Continued)
A
AB
00
01
11
10
00
1
1
0
0
01
1
1
1
1
CD
A
AB
00
01
11
10
00
1
1
0
0
01
1
1
1
1
CD
D
11
0
0
1
D
1
C
11
0
0
1
1
10
1
1
1
1
C
10
1
1
1
1
B
B
Second EXPAND generates a
different set of prime implicants
IRREDUNDANT COVER found by
final step of espresso
ECE C03 Lecture 3
Only three prime implicants!
30

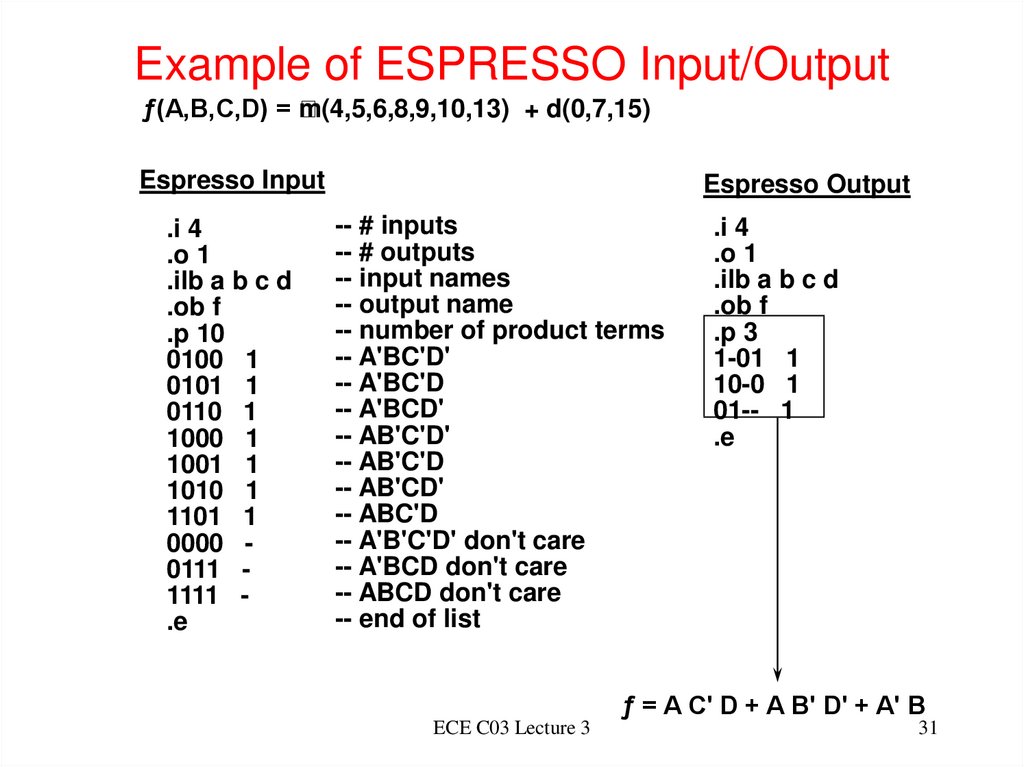
31. Example of ESPRESSO Input/Output

ƒ(A,B,C,D) = 
m(4,5,6,8,9,10,13) + d(0,7,15)
Espresso Input
.i 4
.o 1
.ilb a b c d
.ob f
.p 10
0100 1
0101 1
0110 1
1000 1
1001 1
1010 1
1101 1
0000 0111 1111 .e
Espresso Output
-- # inputs
-- # outputs
-- input names
-- output name
-- number of product terms
-- A'BC'D'
-- A'BC'D
-- A'BCD'
-- AB'C'D'
-- AB'C'D
-- AB'CD'
-- ABC'D
-- A'B'C'D' don't care
-- A'BCD don't care
-- ABCD don't care
-- end of list
.i 4
.o 1
.ilb a b c d
.ob f
.p 3
1-01 1
10-0 1
01-- 1
.e
ƒ = A C' D + A B' D' + A' B
ECE C03 Lecture 3
31

32. Two-Level Logic Design Approach

Primitive logic building blocks
INVERTER, AND, OR, NAND, NOR, XOR, XNOR
Canonical Forms
Sum of Products, Products of Sums
Incompletely specified functions/don't cares
Logic Minimization
Goal: two-level logic realizations with fewest gates and fewest
number of gate inputs
Obtained via Laws and Theorems of Boolean Algebra
or Boolean Cubes and the Uniting Theorem
or K-map Methods up to 6 variables
or Quine-McCluskey Algorithm
or Espresso CAD Tool
ECE C03 Lecture 3
32

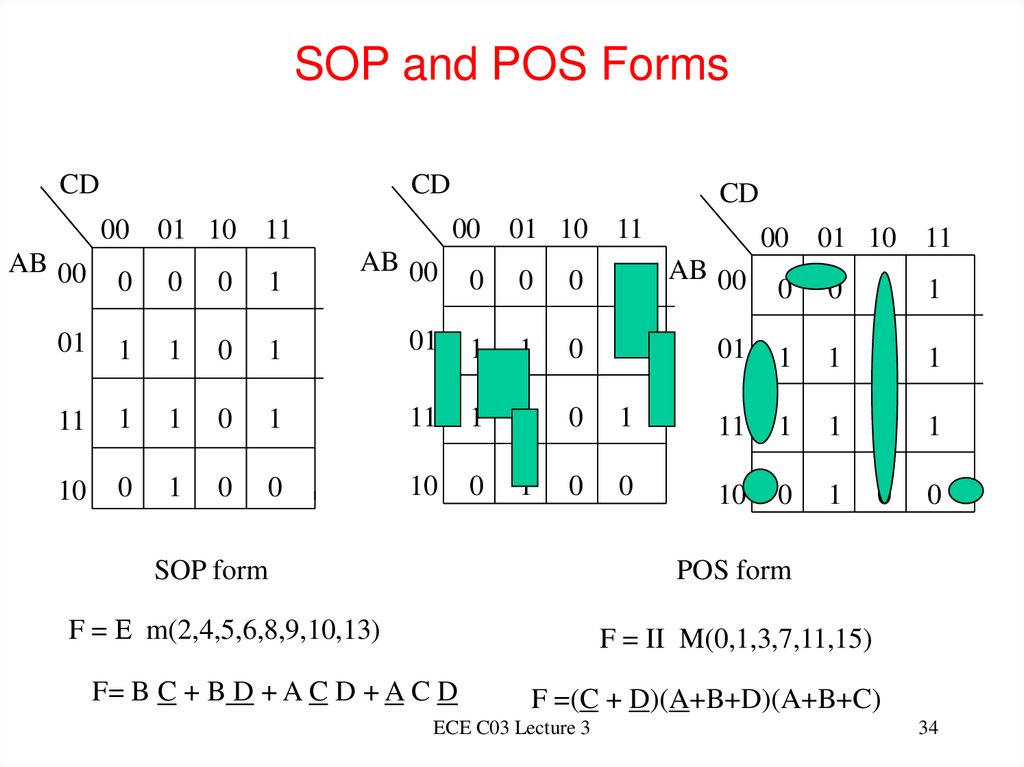
33. SOP and POS Two-Level Logic Forms

• We have looked at two-level logic expressions
• Sum of products form
– F=abc+bcd+abd+ac
– This lists the ON sets of the functions, minterms that
have the value 1
• Product of sums form (another equivalent form)
– F = ( a + b + c ) . ( b + c + d ) . ( a + b + d ) . ( a + c)
– This lists the OFF sets of the functions, maxterms that
have the value 0
• Relationship between forms
– minimal POS form of F = minimal SOP form of F
– minimal SOP form of F = minimal POS form of F
ECE C03 Lecture 3
33

34. SOP and POS Forms

CD
CD
CD
00 01 10 11
00 01 10 11
00 01 10 11
1
AB 00
0
0
0
1
AB 00
0
0
0
1
0
1
01
1
1
0
1
01
1
1
0
1
1
0
1
11
1
1
0
1
11
1
1
0
1
1
0
0
10
0
1
0
0
10
0
1
0
0
AB 00
0
0
0
01
1
1
11
1
10
0
SOP form
POS form
F = E m(2,4,5,6,8,9,10,13)
F = II M(0,1,3,7,11,15)
F= B C + B D + A C D + A C D
F =(C + D)(A+B+D)(A+B+C)
ECE C03 Lecture 3
34

35. Product of Sums Minimization

• For a given function shown as a K-map, in an SOP
realization one groups the 1s
• Example: F= B C + B D + A C D + A C D
• For the same function in a K-map, in a POS realization
one groups the 0s
• Example: F(A,B,C,D) = (C.D) + (A.B.D) + (A.B.C)
• With De Morgan’s theorem
F = (C + D) . (A + B + D) . (A + B + C)
• Can generalize Quine McCluskey and ESPRESSO
techniques for POS forms as well
ECE C03 Lecture 3
35

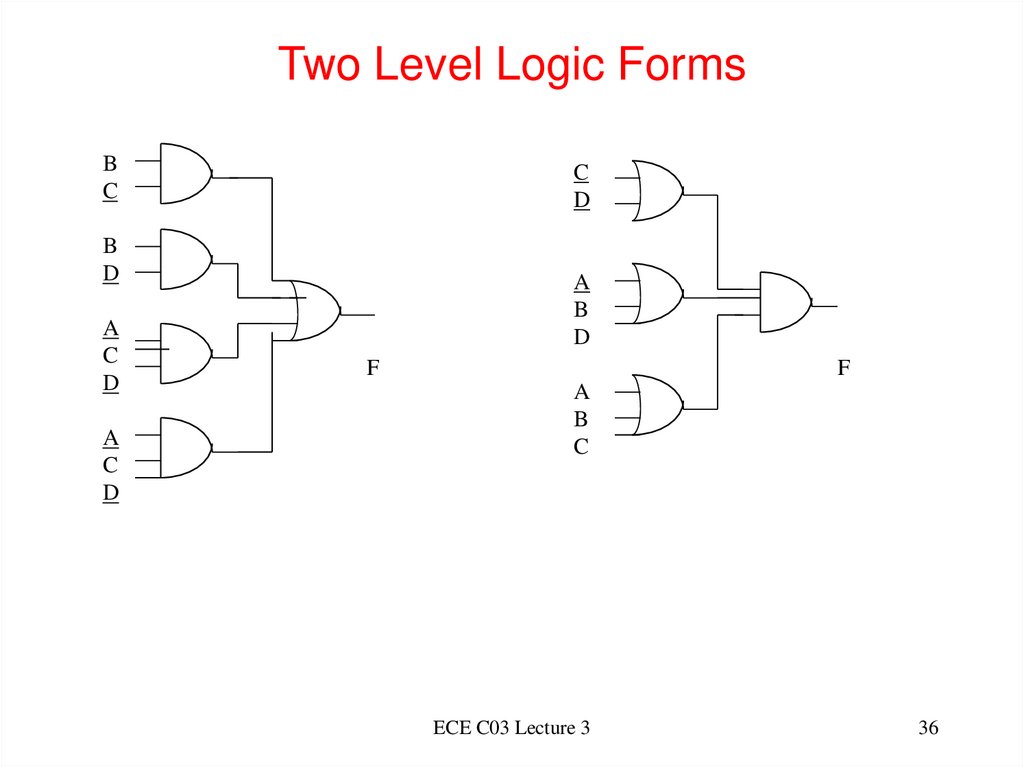
36. Two Level Logic Forms

B
C
C
D
B
D
A
C
D
A
C
D
A
B
D
F
F
A
B
C
ECE C03 Lecture 3
36

37. Summary

CAD Tools for 2-level minimization
Quine-McCluskey Method
ESPRESSO Algorithm
NEXT LECTURE: Combinational Logic
Implementation Technologies
• READING: Katz 4.1, 4.2, Dewey 5.2, 5.3, 5.4,
5.5 5.6, 5.7, 6.2
ECE C03 Lecture 3
37