Similar presentations:
Number System
1. Number System
A number system is defined as a system of writing to express numbers.It is the mathematical notation for representing numbers of a given set by using
digits or other symbols in a consistent manner.
Humans use the DECIMAL system (“deci” stands for “ten”)
To convert data into strings of numbers, computers use the BINARY number system
Elementary storage units inside computers are electronic switches.
Each switch holds one of two states: on (1) or off (0).
ON
OFF
We use a bit (binary digit), 0 or 1, to represent the state.
0 (00)
1 (01)
2 (10)
3 (11)
2.
Bits and BytesA bit is the smallest unit of information a computer can use, having a value of 1 or 0.
Computers work with collections of bits, grouping them to represent larger pieces of data,
such as letters of the alphabet.
Eight bits make up one byte. A byte is the amount of memory needed to store one
alphanumeric character.
With one byte, the computer can represent one of 256 different symbols or characters.
1 01
10
1 01
01 1 01
3. Common Number Systems
SystemBase
Symbols
Decimal
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binary
2
0, 1
Octal
8
0, 1, 2, 3, 4, 5, 6, 7, 10, ….
Hexadecimal
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
A, B, C, D, E, F, 10, …
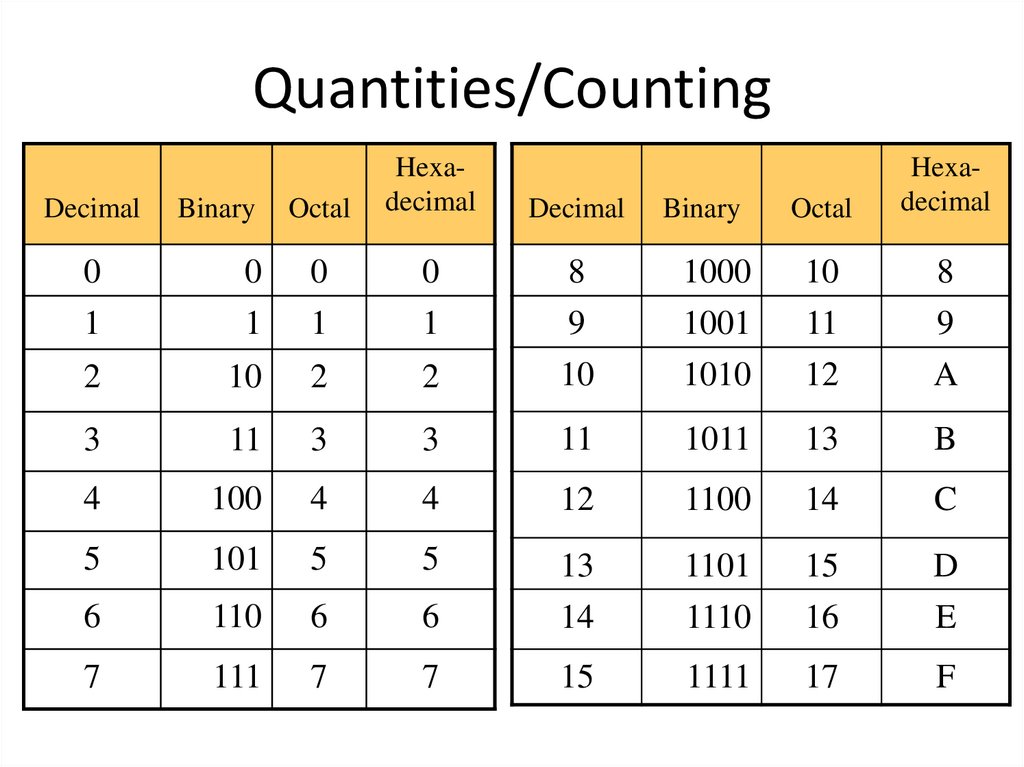
4. Quantities/Counting
DecimalBinary
Octal
Hexadecimal
Decimal
Binary
Octal
Hexadecimal
1000
1001
1010
10
11
12
8
9
A
0
1
0
1
0
1
0
1
2
10
2
2
8
9
10
3
11
3
3
11
1011
13
B
4
100
4
4
12
1100
14
C
5
101
5
5
6
110
6
6
13
14
1101
1110
15
16
D
E
7
111
7
7
15
1111
17
F
5. Decimal to Binary
Repeated Division-by-2 Method (for whole number)To convert a whole number to binary, use successive division by 2 until the quotient
is 0. The remainders form the answer, with the first remainder as the least
significant bit (LSB) and the last as the most significant bit (MSB).
(43)10 = (101011)2
6. Example
12510 = ?22 125
2 62
2 31
2 15
7
2
3
2
1
1
0
1
1
1
1
12510 = 11111012
7. Binary to Decimal
• Technique– Multiply each bit by 2n, where n is the “weight” of
the bit
– The weight is the position of the bit, starting from
0 on the right
– Add the results
8. Example
Bit “0”1010112 =>
1 x 20 =
1 x 21 =
0 x 22 =
1 x 23 =
0 x 24 =
1 x 25 =
1
2
0
8
0
32
4310
9. Decimal to Octal
• Technique– Divide by 8
– Keep track of the remainder
10. Example
123410 = ?88
8
8
8
1234
154
19
2
2
2
3
123410 = 23228
11. Octal to Decimal
• Technique– Multiply each bit by 8n, where n is the “weight” of
the bit
– The weight is the position of the bit, starting from
0 on the right
– Add the results
12. Example
7248 =>4 x 80 =
2 x 81 =
7 x 82 =
4
16
448
46810
13. Decimal to Hexadecimal
• Technique– Divide by 16
– Keep track of the remainder
14. Example
123410 = ?1616
16
16
1234
77
4
2
13 = D
123410 = 4D216
15. Hexadecimal to Decimal
• Technique– Multiply each bit by 16n, where n is the “weight”
of the bit
– The weight is the position of the bit, starting from
0 on the right
– Add the results
16. Example
ABC16 =>C x 160 = 12 x
1 =
12
B x 161 = 11 x 16 = 176
A x 162 = 10 x 256 = 2560
274810
17. Exercise – Convert ...
Decimal33
Binary
Octal
Hexadecimal
1110101
703
1AF
Don’t use a calculator!
Skip answer
Answer
18. Exercise – Convert …
AnswerHexadecimal
Decimal
33
Binary
100001
Octal
41
117
1110101
165
75
451
111000011
703
1C3
431
110101111
657
1AF
21


















 programming
programming








