Стеценко_Инна_В (1)

1.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ПЕТРИ-ОБЪЕКТНОГО
МОДЕЛИРОВАНИЯ СИСТЕМ
Стеценко Инна Вячеславовна
к.т.н., доцент кафедры системного анализа и
методов принятия решений
Черкасского государственного
технологического университета,
соискатель доктора технических наук
Института проблем математических машин и
систем
Научный консультант
д.т.н., проф. Литвинов В.В.

2. Актуальность разработки

“...И пока у нас нет ни математических
инструментов, ни интеллектуальных возможностей
для полного моделирования поведения больших
дискретных систем...”
Гради Буч
Актуальность разработки
обусловлена
возрастающей сложностью задач, которые ставятся перед разработчиками
информационных технологий,
повышением требований к скорости построения модели и скорости получения
результатов моделирования,
стремительным развитием электронных средств сбора и хранения данных
необходимостью интеграции с другими технологиями,
недостатками существующих технологий моделирования:
o
o
o
o
ограниченность используемых средств формализации,
необходимость использования различных средств формализации для
моделирования объекта управления и подсистемы управления,
недостаточный уровень детализации процессов управления,
большая трудоемкость построения моделей сложных систем.

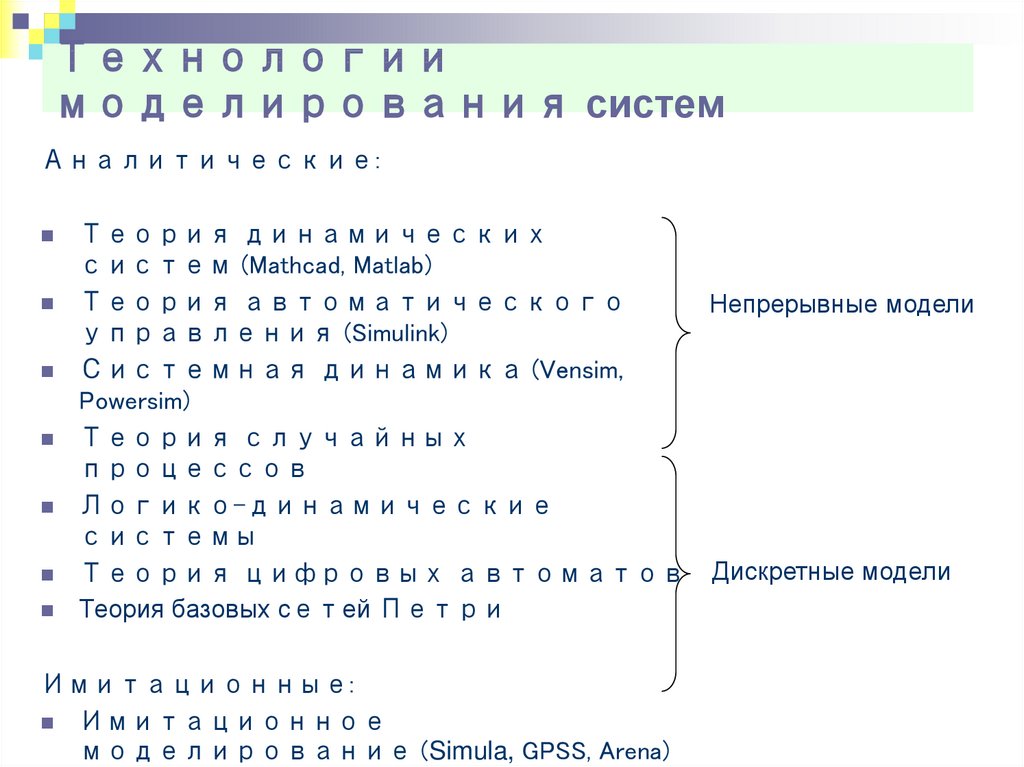
3. Технологии моделирования систем

Аналитические:
Теория динамических
систем (Mathcad, Matlab)
Теория автоматического
Непрерывные модели
управления (Simulink)
Системная динамика (Vensim,
Powersim)
Теория случайных
процессов
Логико-динамические
системы
Теория цифровых автоматов Дискретные модели
Теория базовых сетей Петри
Имитационные:
Имитационное
моделирование (Simula, GPSS, Arena)

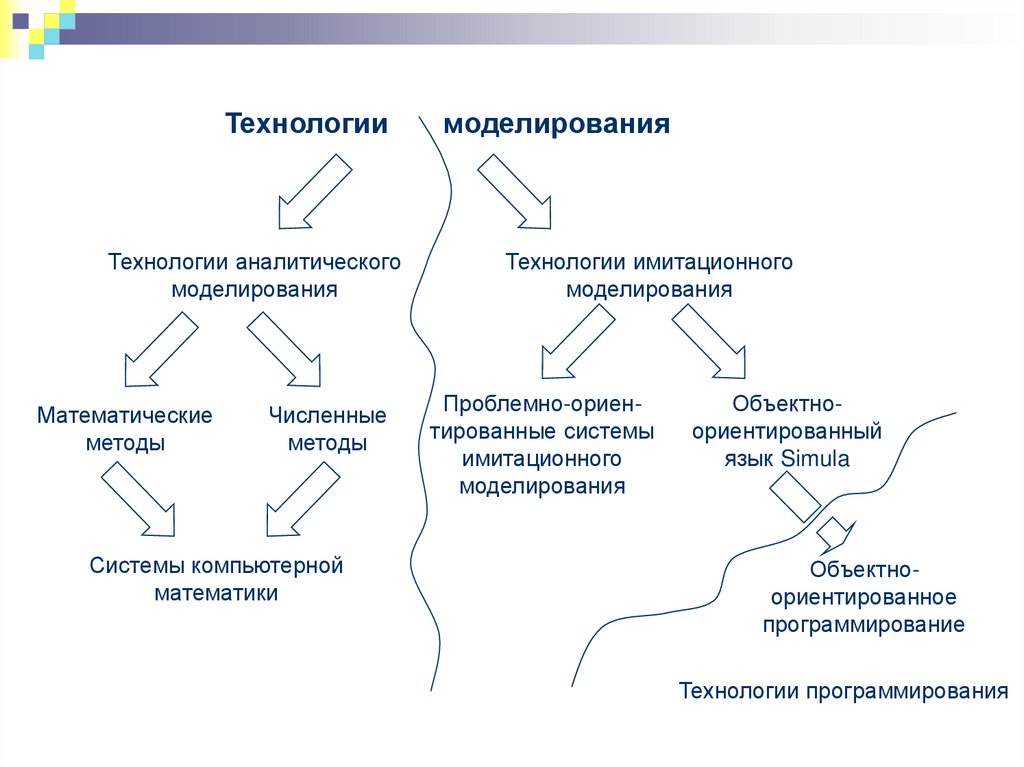
4.

Технологии
Технологии аналитического
моделирования
Математические
методы
Численные
методы
Системы компьютерной
математики
моделирования
Технологии имитационного
моделирования
Проблемно-ориентированные системы
имитационного
моделирования
Объектноориентированный
язык Simula
Объектноориентированное
программирование
Технологии программирования

5. Сети Петри как средство формализации дискретно-событийных процессов управления

Сети Петри как средство
формализации дискретнособытийных процессов
управления
Преимущества сетей Петри
Высокий уровень формализации дискретно-событийных систем
Аналитическое исследование свойств модели
Возможность применения к немарковским процессам функционирования
Murata Т. Petri nets: Properties, Analysis and Applications // Proceedings of the IEEE. - April,
1989. - vol.77, No.44. – P. 541-580.
Питерсон Дж. Теория сетей Петри и моделирование систем. - М.: Мир, 1984. – 264 с.
Котов В.Е. Сети Петри. - М.: Наука, 1984. - 158 с.
Зайцев Д.А. Инварианты временных сетей Петри // Кибернетика и системный анализ. –
2004. - №2. - С.92-106.
Haas P. J. Stochastic Petri nets : modelling, stability, simulation / Peter J. Haas — Springer
series in operations research. – 2002. -– 529p.
Возможность быстрого конструирования алгоритма имитации системы с большим
количеством событий
Вычислимость алгоритма имитации сети Петри гарантируется эквивалентностью
приоритетной сети Петри машине Тьюринга
Котов В.Е. Сети Петри. - М.: Наука, 1984. - 158 с.

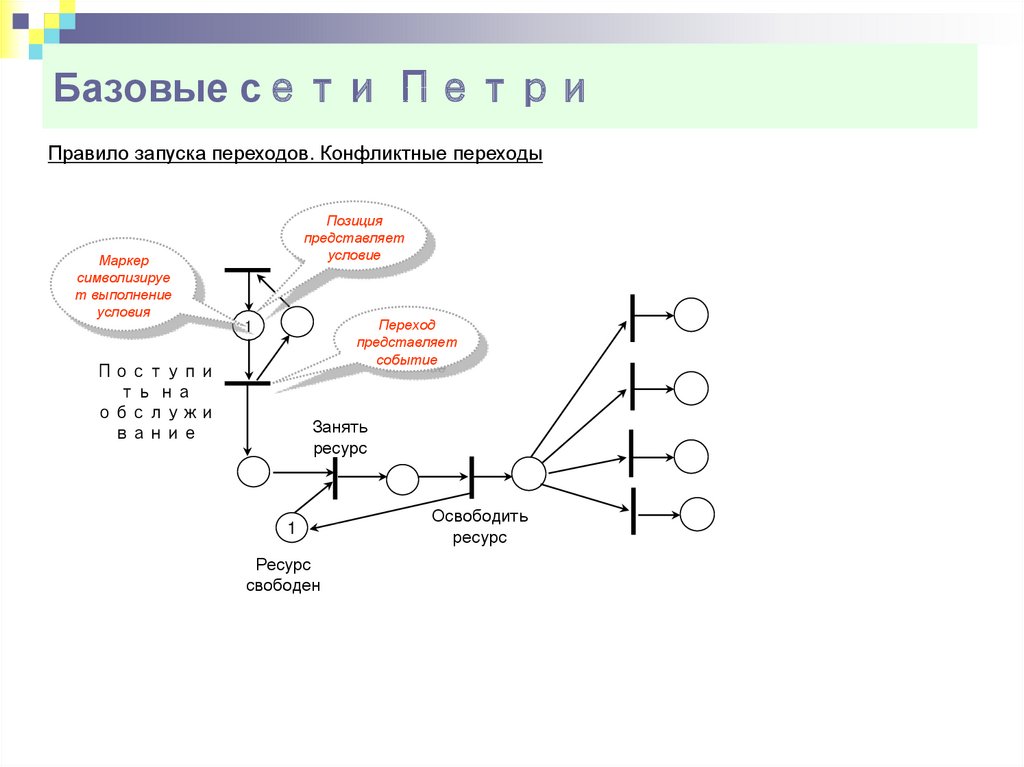
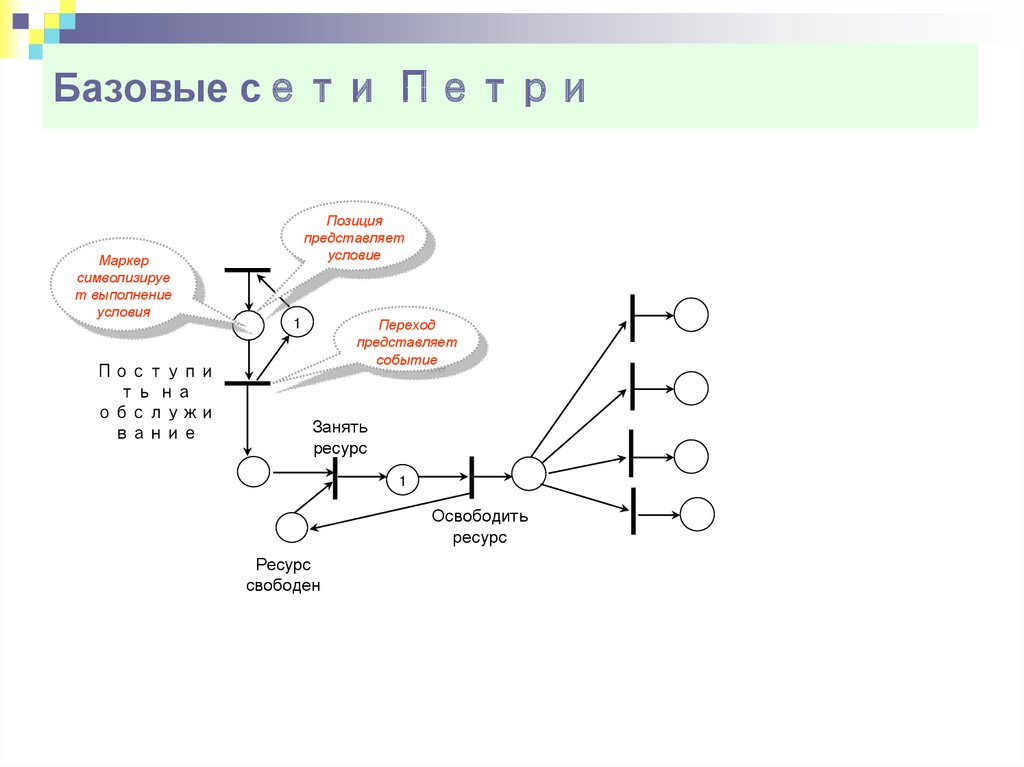
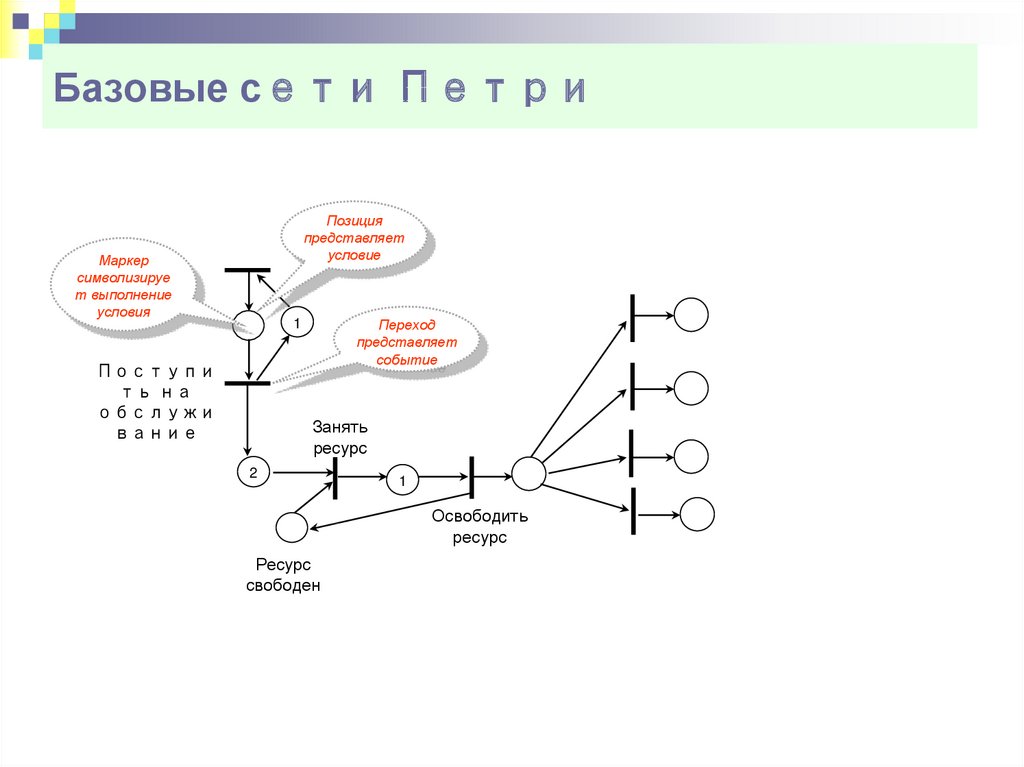
6. Базовые сети Петри

Правило запуска переходов. Конфликтные переходы
Маркер
символизируе
т выполнение
условия
Позиция
представляет
условие
Переход
представляет
событие
1
Поступи
ть на
обслужи
вание
Занять
ресурс
1
Ресурс
свободен
Освободить
ресурс

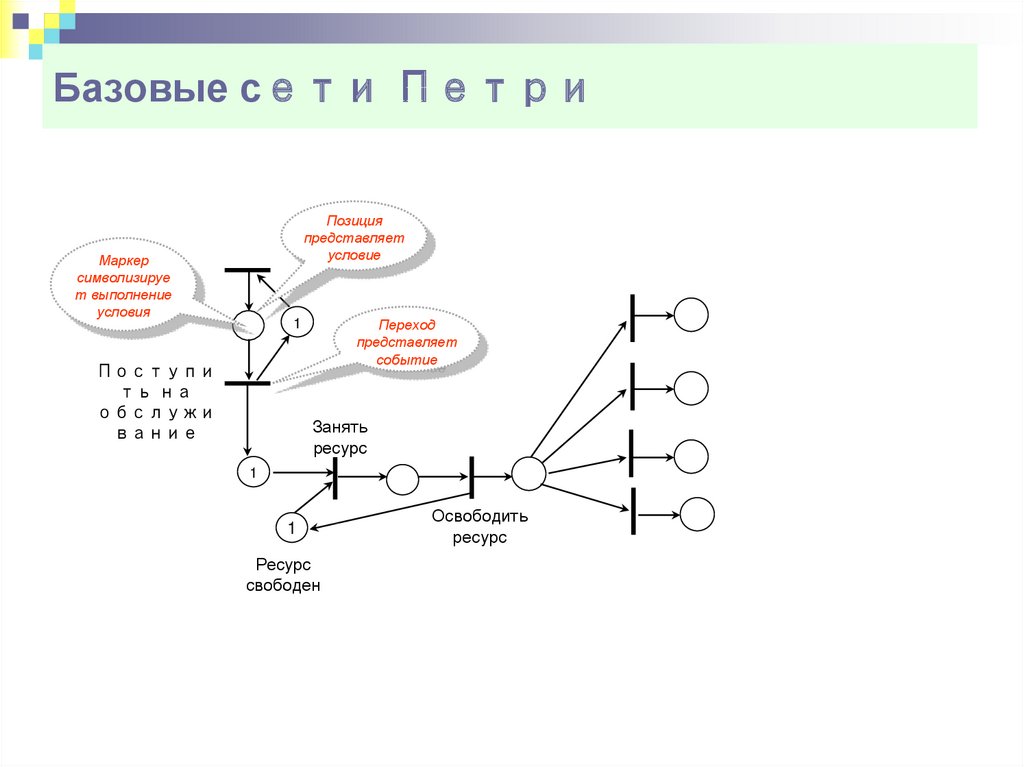
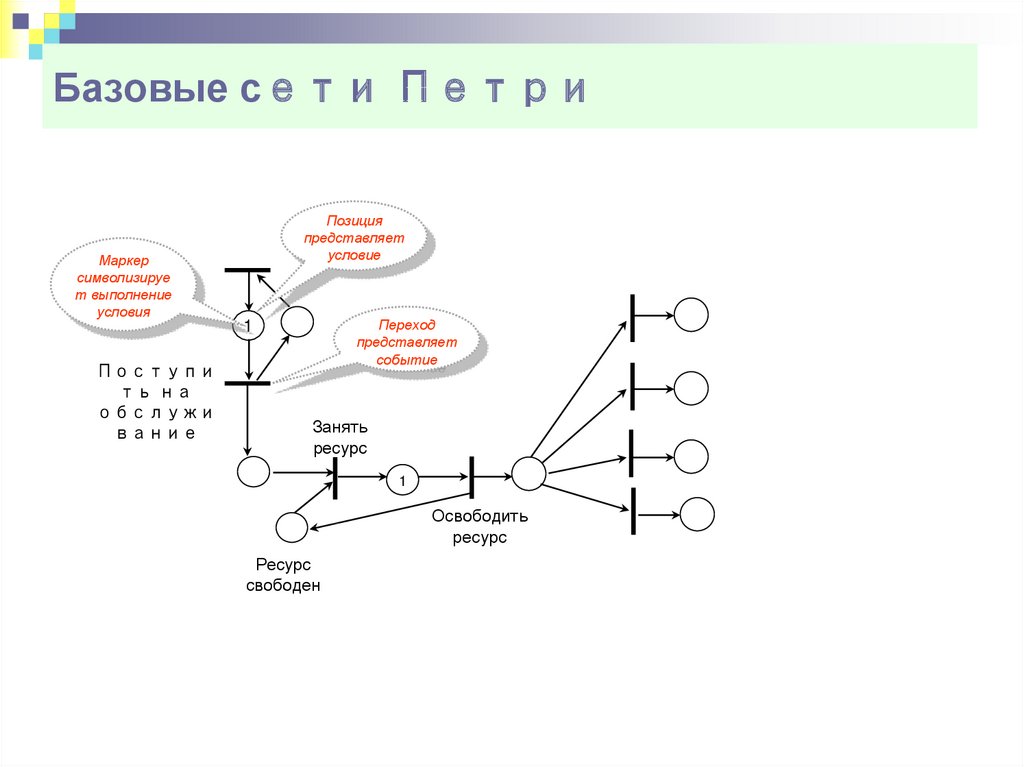
7. Базовые сети Петри

Позиция
представляет
условие
Маркер
символизируе
т выполнение
условия
Переход
представляет
событие
1
Поступи
ть на
обслужи
вание
Занять
ресурс
1
1
Ресурс
свободен
Освободить
ресурс

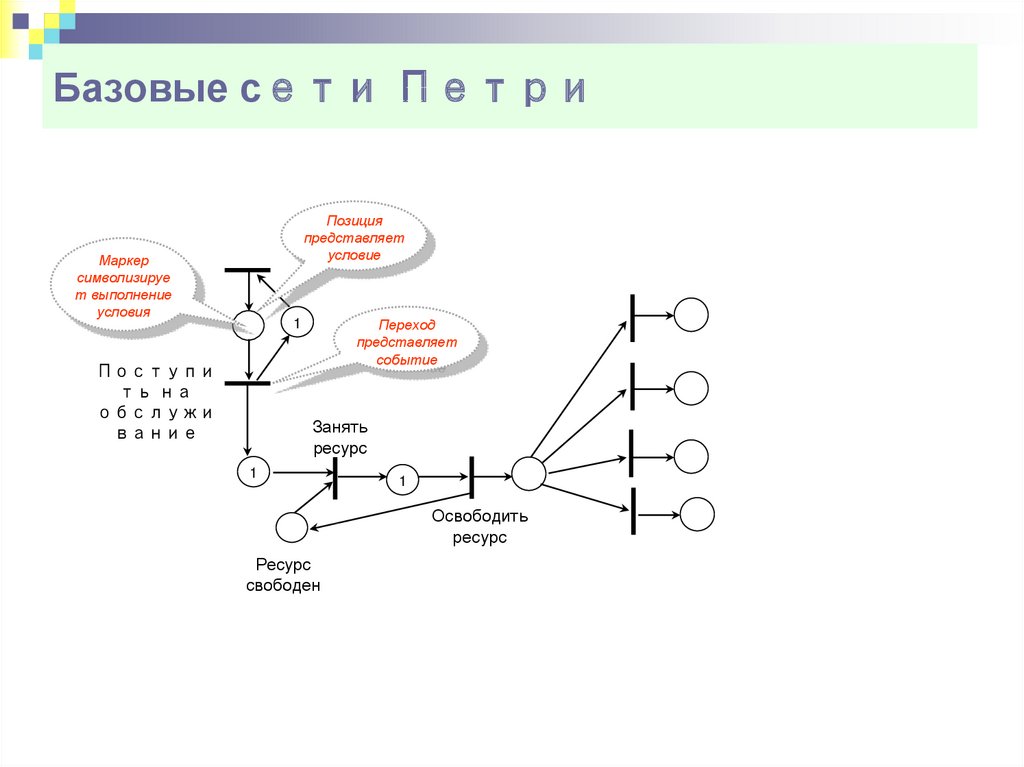
8. Базовые сети Петри

Маркер
символизируе
т выполнение
условия
Поступи
ть на
обслужи
вание
Позиция
представляет
условие
Переход
представляет
событие
1
Занять
ресурс
1
Освободить
ресурс
Ресурс
свободен

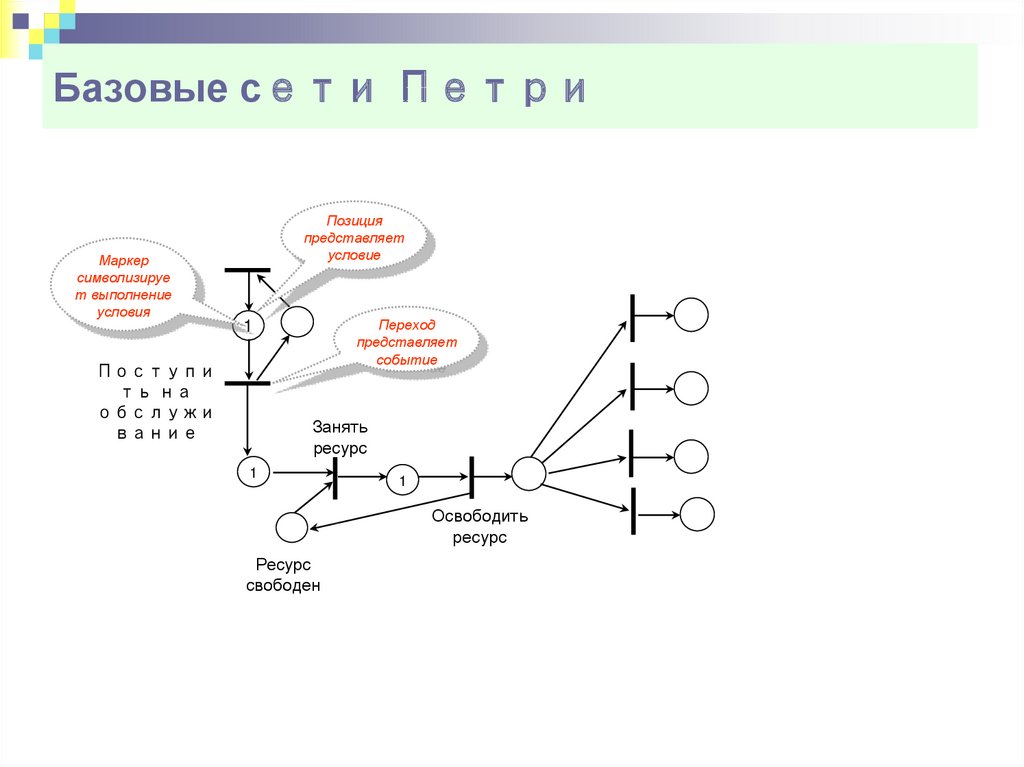
9. Базовые сети Петри

Маркер
символизируе
т выполнение
условия
Поступи
ть на
обслужи
вание
Позиция
представляет
условие
Переход
представляет
событие
1
Занять
ресурс
1
Освободить
ресурс
Ресурс
свободен

10. Базовые сети Петри

Позиция
представляет
условие
Маркер
символизируе
т выполнение
условия
Переход
представляет
событие
1
Поступи
ть на
обслужи
вание
Занять
ресурс
1
1
Освободить
ресурс
Ресурс
свободен

11. Базовые сети Петри

Маркер
символизируе
т выполнение
условия
Позиция
представляет
условие
Переход
представляет
событие
1
Поступи
ть на
обслужи
вание
Занять
ресурс
1
1
Освободить
ресурс
Ресурс
свободен

12. Базовые сети Петри

Позиция
представляет
условие
Маркер
символизируе
т выполнение
условия
Переход
представляет
событие
1
Поступи
ть на
обслужи
вание
Занять
ресурс
2
1
Освободить
ресурс
Ресурс
свободен

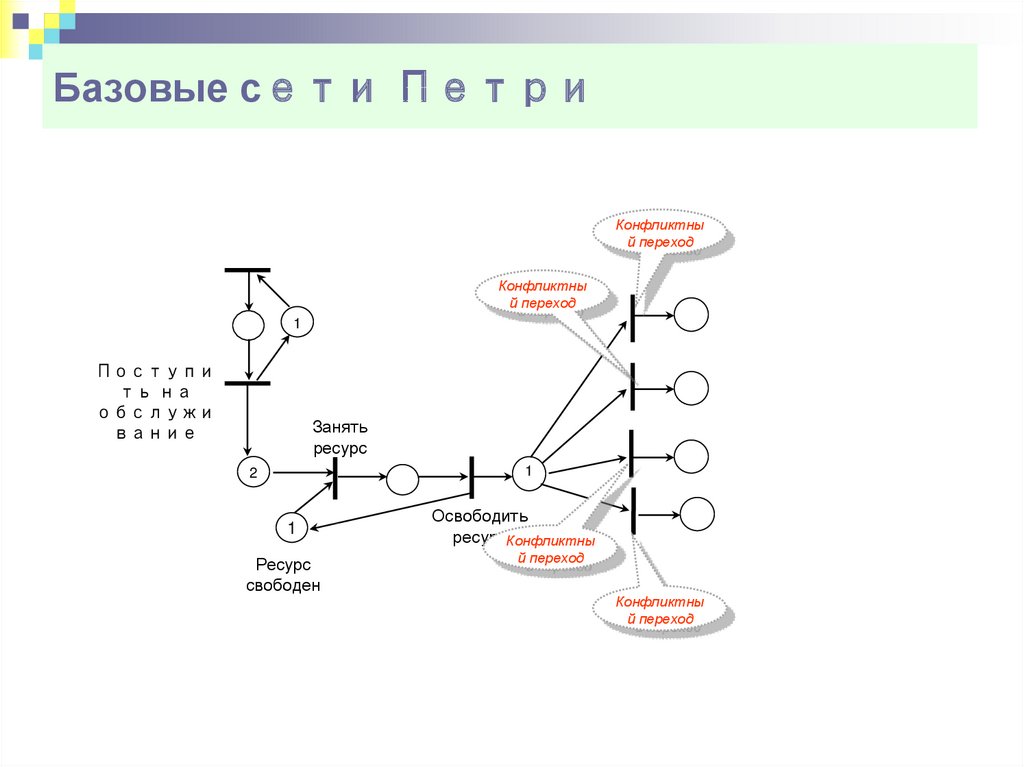
13. Базовые сети Петри

Конфликтны
й переход
Конфликтны
й переход
1
Поступи
ть на
обслужи
вание
Занять
ресурс
1
2
1
Ресурс
свободен
Освободить
ресурсКонфликтны
й переход
Конфликтны
й переход

14. Базовые сети Петри

Конфликтны
й переход
Конфликтны
й переход
1
Поступи
ть на
обслужи
вание
1
Занять
ресурс
2
1
Ресурс
свободен
Освободить
ресурсКонфликтны
й переход
Конфликтны
й переход

15. Базовые сети Петри

Конфликтны
й переход
Конфликтны
й переход
1
Поступи
ть на
обслужи
вание
23
27
Занять
ресурс
1
Ресурс
свободен
21
Освободить
ресурсКонфликтны
19
й переход
Конфликтны
й переход

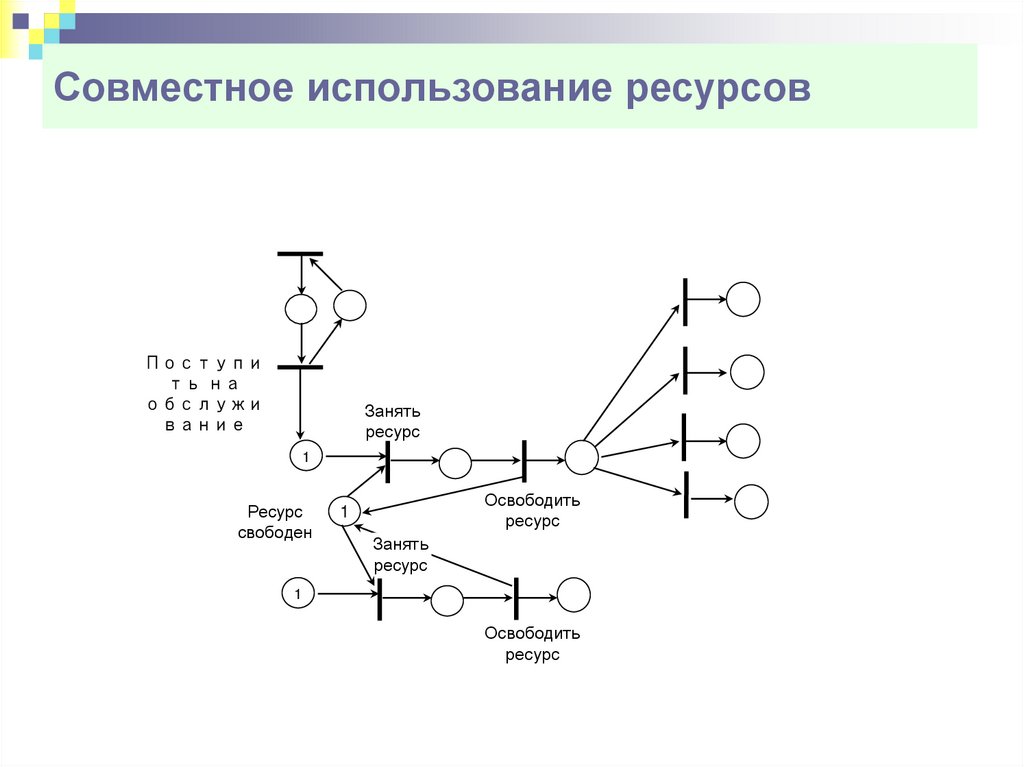
16. Совместное использование ресурсов

Поступи
ть на
обслужи
вание
Занять
ресурс
1
Ресурс
свободен
Освободить
ресурс
1
Занять
ресурс
1
Освободить
ресурс

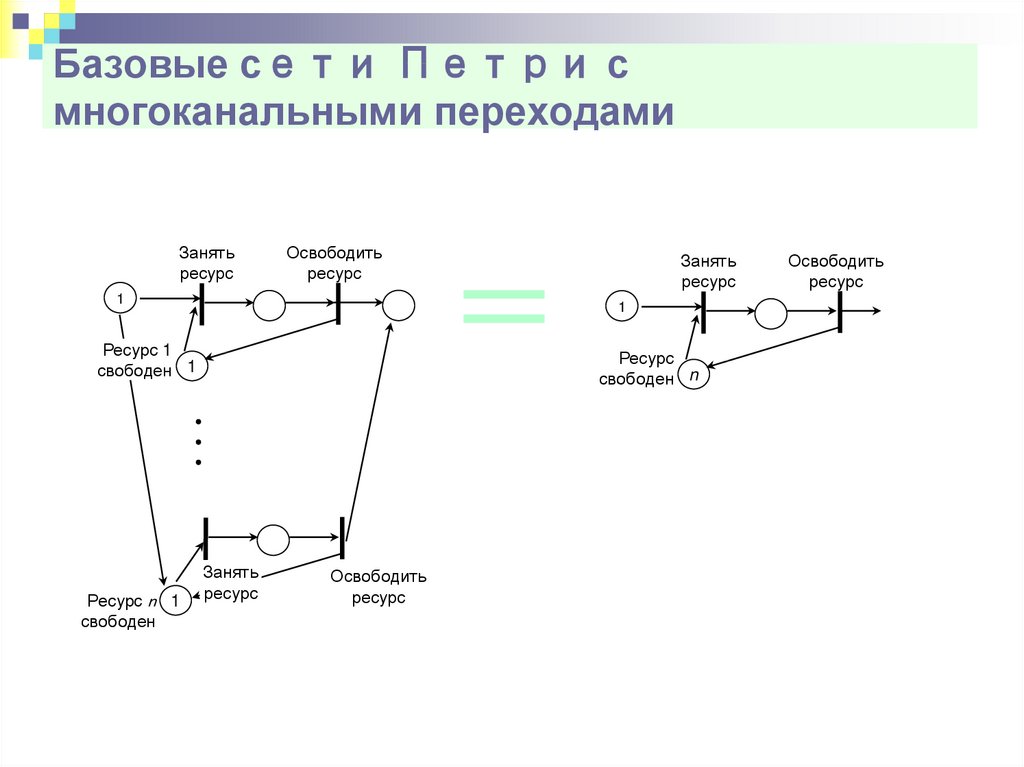
17. Базовые сети Петри с многоканальными переходами

Занять
ресурс
Освободить
ресурс
1
1
Ресурс 1
свободен 1
Ресурс n 1
свободен
Занять
ресурс
Ресурс
свободен n
Занять
ресурс
Освободить
ресурс
Освободить
ресурс

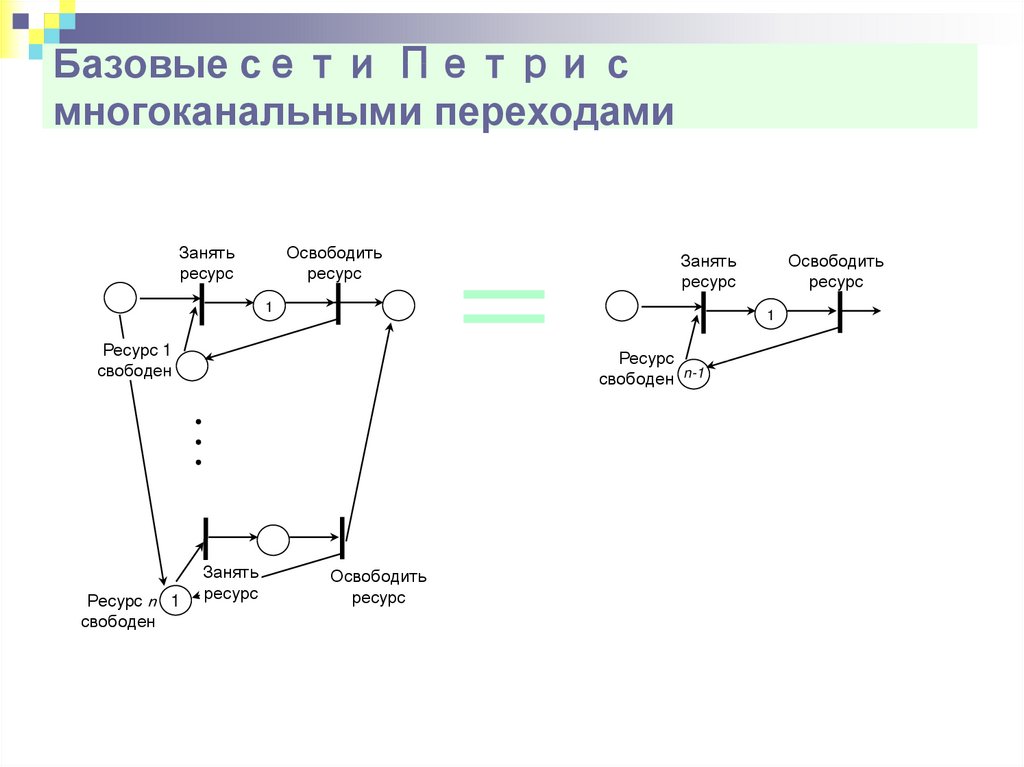
18. Базовые сети Петри с многоканальными переходами

Занять
ресурс
Освободить
ресурс
Занять
ресурс
1
1
Ресурс 1
свободен
Ресурс n 1
свободен
Ресурс
свободен n-1
Занять
ресурс
Освободить
ресурс
Освободить
ресурс

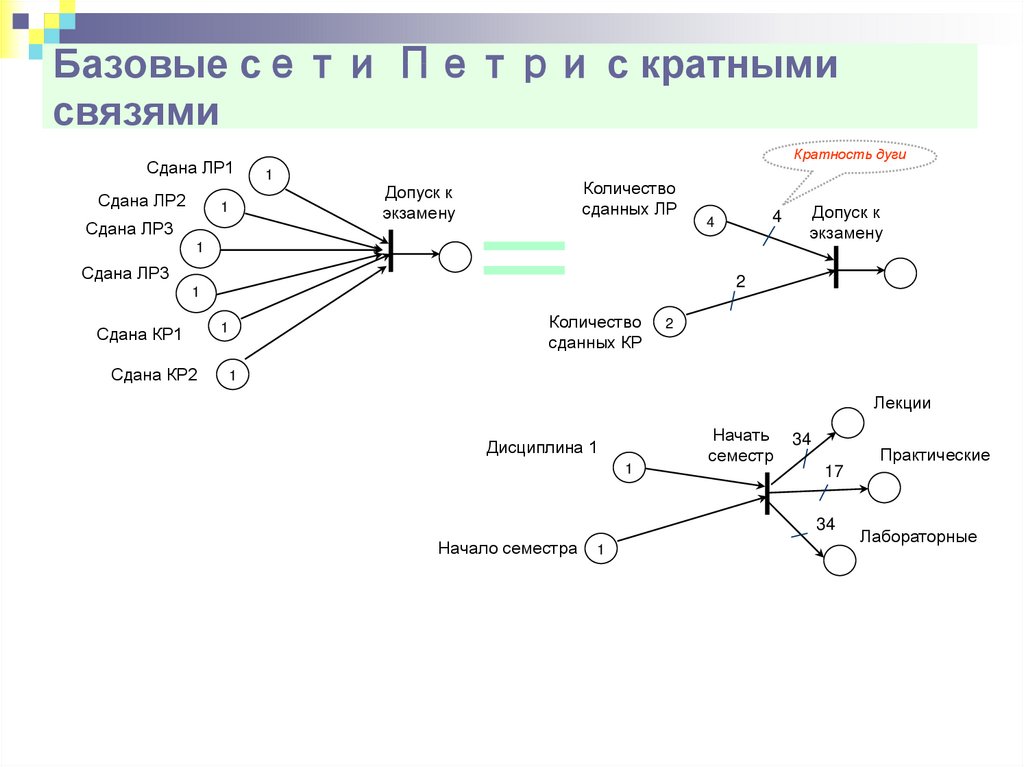
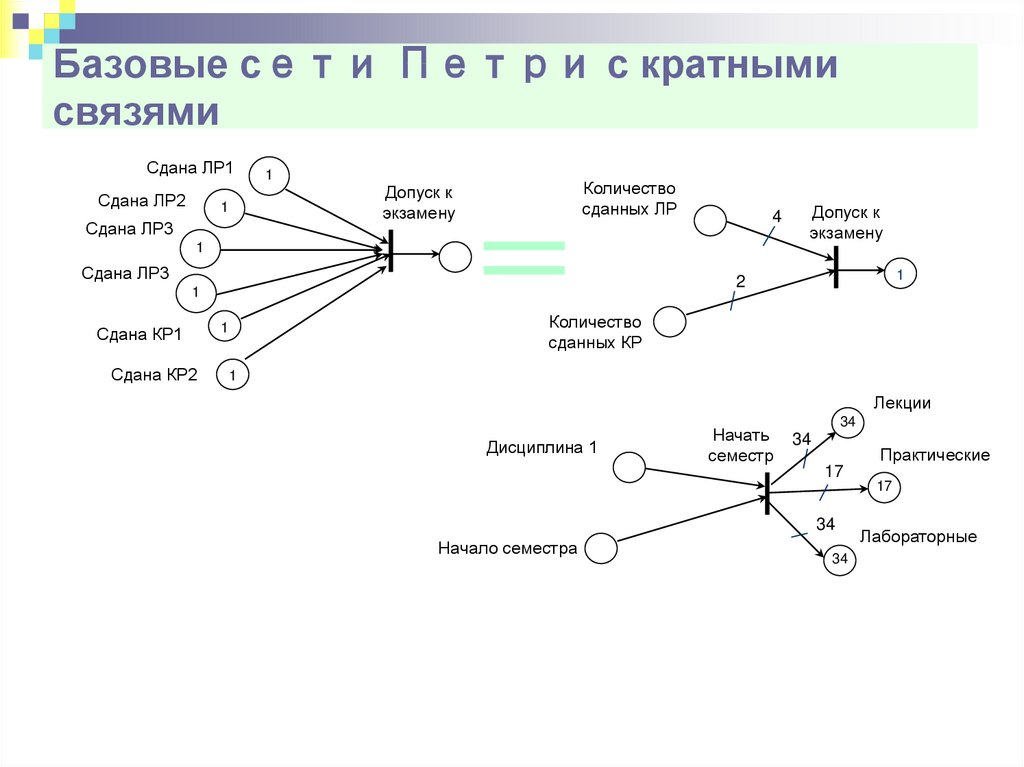
19. Базовые сети Петри с кратными связями

Сдана ЛР1
Сдана ЛР2
1
Сдана ЛР3
Кратность дуги
1
Количество
сданных ЛР
Допуск к
экзамену
4
4
1
Сдана ЛР3
2
1
Сдана КР1
Сдана КР2
Допуск к
экзамену
Количество
сданных КР
1
2
1
Лекции
Дисциплина 1
1
Начать
семестр
34
Практические
17
34
Начало семестра
1
Лабораторные

20. Базовые сети Петри с кратными связями

Сдана ЛР1
Сдана ЛР2
1
Сдана ЛР3
1
Количество
сданных ЛР
Допуск к
экзамену
4
1
Сдана ЛР3
Сдана КР2
1
2
1
Сдана КР1
Допуск к
экзамену
Количество
сданных КР
1
1
Лекции
Дисциплина 1
Начать
семестр
34
34
Практические
17
34
Начало семестра
34
17
Лабораторные

21.

Математическое описание
базовой сети Петри
[Murata T. Petri Nets: Properties, Analysis and Applications. // Proceedings of IEEE.
– 1989. - Vol.77, No.4. - P.541-580.]
N ( P, T, A, W )
Базовая сеть Петри
W: A
- кратности дуг
P P
- множество
позиций
T T
- множество
переходов
A P T T P
- множество дуг
P T
Состояние сети Петри:
M M P | M P Z , P P
- состояние позиций
T, T
- множество входных и множество выходных позиций перехода Т
P, P
- множество входных и множество выходных переходов позиции Р
Условие запуска перехода Т сети Петри:
Запуск перехода Т сети Петри:
P T
M P WP,T
P T M P M P WP,T
P T M P M P WT , P

22. Матричные уравнения состояний базовой сети Петри

WT , P , T P
a
0, T P
WP ,T , T P
aP ,T
0, T P
P ,T
M || M P ||
a aT , P
- матрица выходов
a aT , P
- матрица входов
- вектор маркировки
a a a
- матрица изменений
Фундаментальное уравнение состояний базовой сети Петри:
Mn M0 a x
x
- вектор количества запусков переходов
a x 0 - Т-инвариант (цикличность функционирования)
aT y 0 - S-инвариант (консервативность системы)

23. Теория базовых сетей Петри

Классификация сетей Петри: безопасные,
ординарные, автоматные и др.
Аналитическое исследование свойств
модели
Murata Т. Petri nets: Properties, Analysis and Applications // Proceedings of
the IEEE. - April, 1989. - vol.77, No.44. – P. 541-580.
Питерсон Дж. Теория сетей Петри и
моделирование систем. - М.: Мир, 1984. – 264 с.
Матричные уравнения состояний,
исследование свойств через
исследование инвариантов поведения и
инвариантов состояний
Расширения сетей Петри: ингибиторные,
приоритетные, синхронные,
самомодифицирующиеся, раскрашенные
сети Петри
Вычислимость сети Петри гарантируется эквивалентностью приоритетной
сети Петри и ингибиторной сети Петри машине Тьюринга

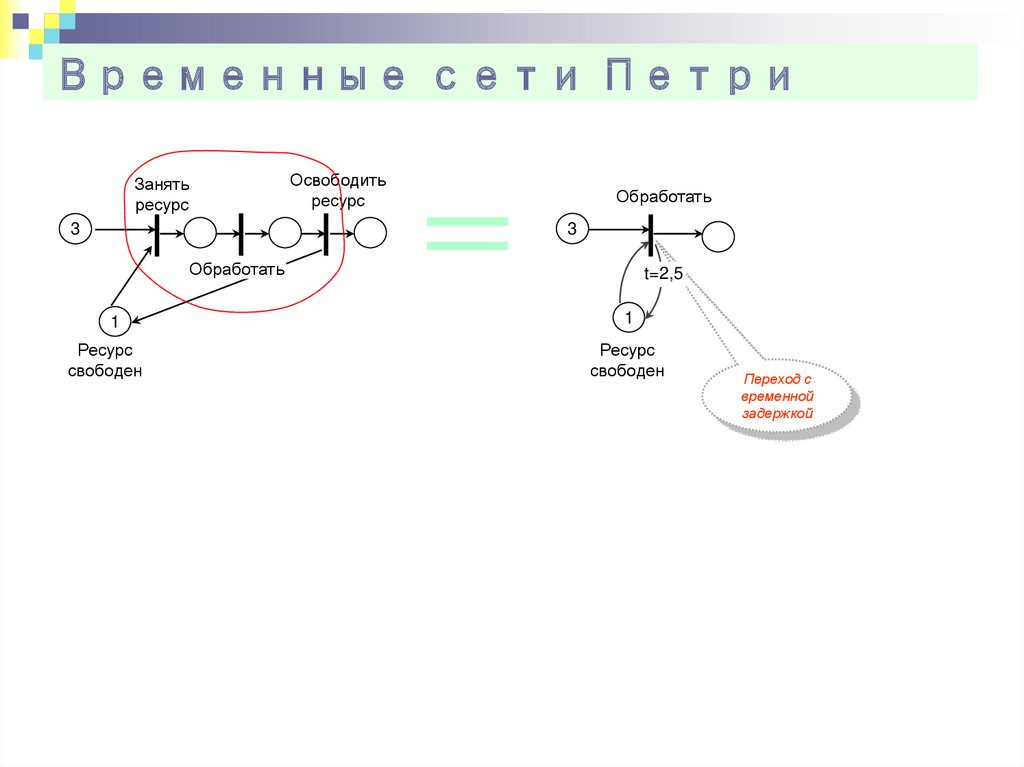
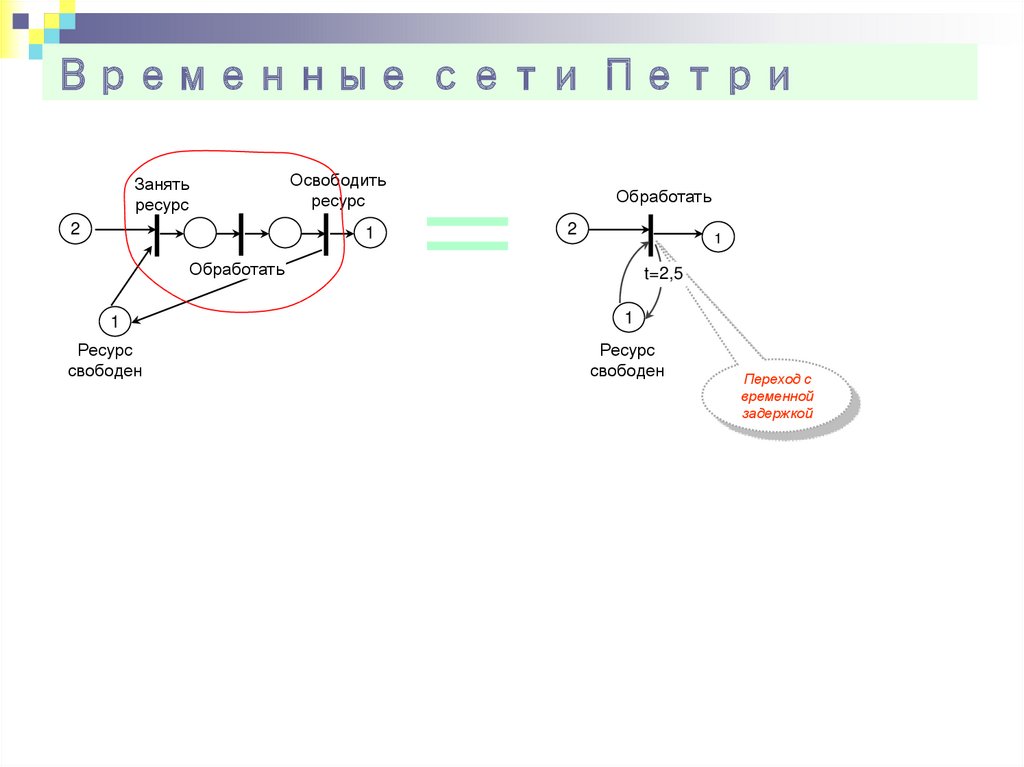
24. Временные сети Петри

Занять
ресурс
Освободить
ресурс
Обработать
3
3
Обработать
1
Ресурс
свободен
t=2,5
1
Ресурс
свободен
Переход с
временной
задержкой

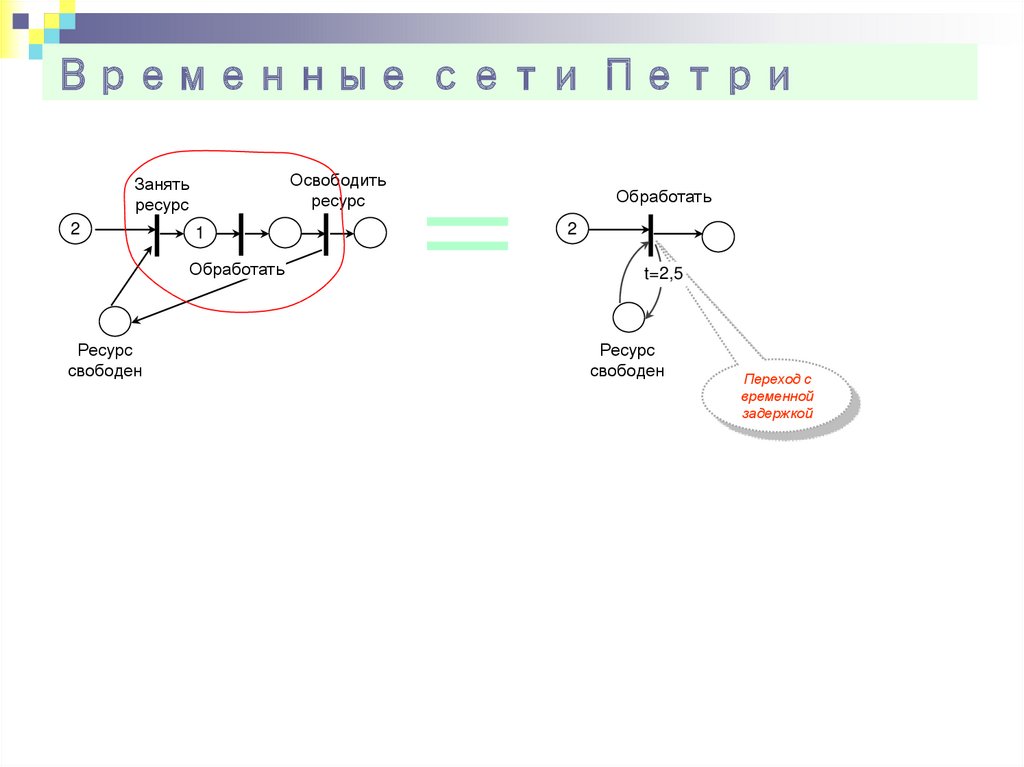
25. Временные сети Петри

Освободить
ресурс
Занять
ресурс
2
1
Обработать
Ресурс
свободен
Обработать
2
t=2,5
Ресурс
свободен
Переход с
временной
задержкой

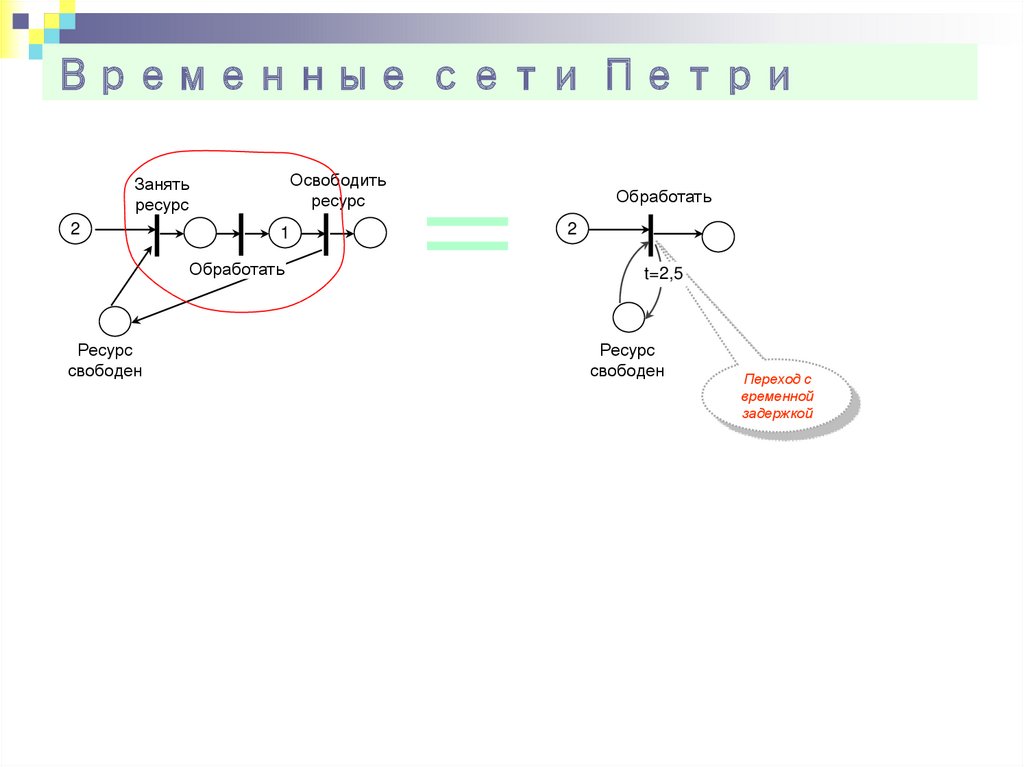
26. Временные сети Петри

Освободить
ресурс
Занять
ресурс
2
1
Обработать
Ресурс
свободен
Обработать
2
t=2,5
Ресурс
свободен
Переход с
временной
задержкой

27. Временные сети Петри

Занять
ресурс
2
Освободить
ресурс
1
Обработать
2
1
Обработать
1
Ресурс
свободен
t=2,5
1
Ресурс
свободен
Переход с
временной
задержкой

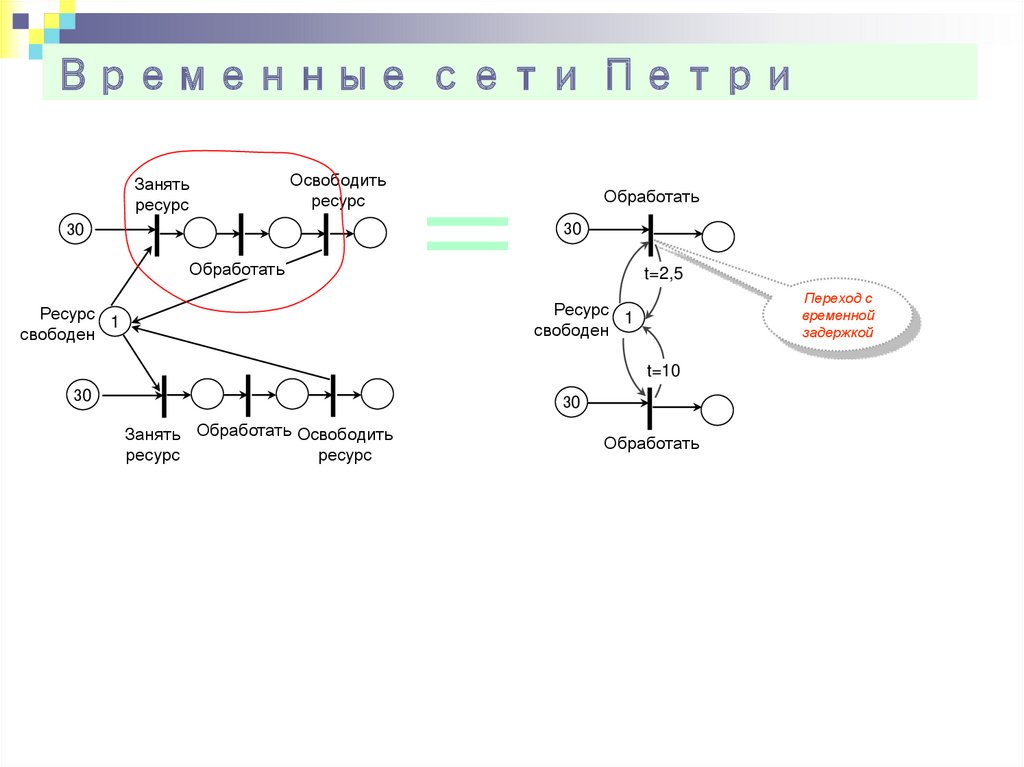
28. Временные сети Петри

Занять
ресурс
Освободить
ресурс
Обработать
30
30
Обработать
t=2,5
Переход с
временной
задержкой
Ресурс 1
свободен
Ресурс 1
свободен
t=10
30
30
Занять Обработать Освободить
ресурс
ресурс
Обработать

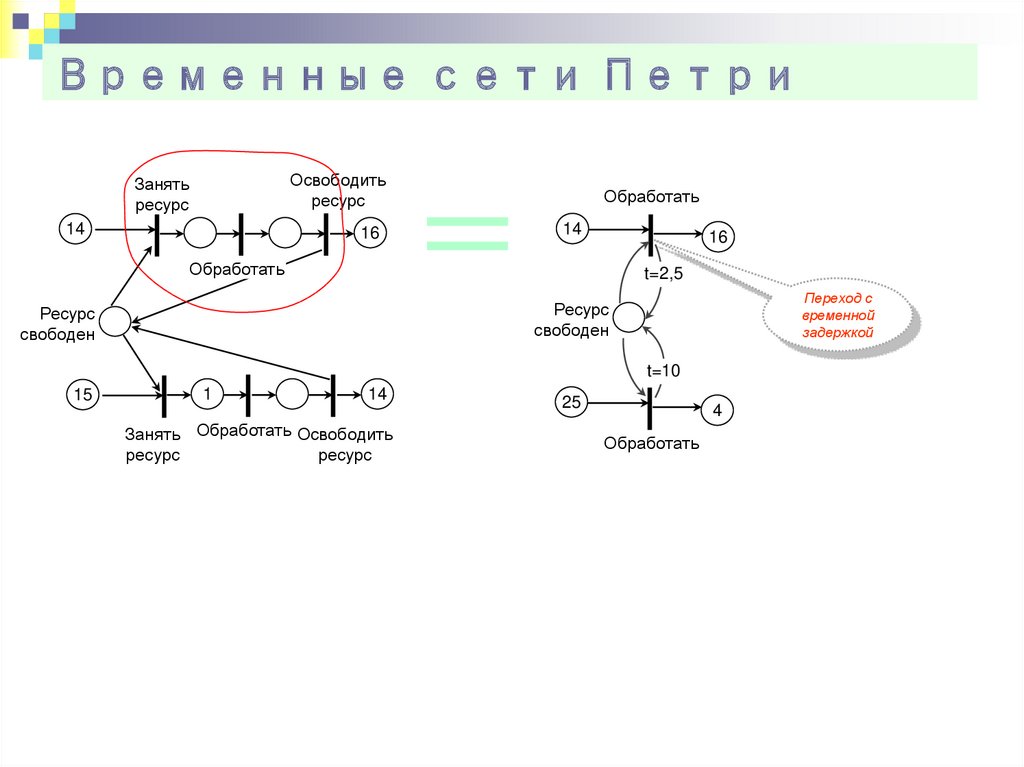
29. Временные сети Петри

Освободить
ресурс
Занять
ресурс
14
16
Обработать
14
16
Обработать
t=2,5
Переход с
временной
задержкой
Ресурс
свободен
Ресурс
свободен
t=10
15
1
14
Занять Обработать Освободить
ресурс
ресурс
25
4
Обработать

30. Теория временных сетей Петри

Классификация, исследование свойств
Wang J. Timed Petri Nets: Theory and Application / J. Wang. - Kluwer
Academic Publishers, USA Octоber, 1998. - 290p.
Фундаментальные уравнения состояний детерминированной временной сети
Петри, матричные уравнения состояний, исследование свойств через
исследование инвариантов поведения и инвариантов состояний
Зайцев Д.А. Инварианты временных сетей Петри // Кибернетика и
системный анализ. – 2004. - №2. - С.92-106.
Применения стохастической сети Петри к немарковским процессам
функционирования
Haas P. J. Stochastic Petri nets : modelling, stability, simulation / Peter J.
Haas — Springer series in operations research. – 2002. -– 529p.

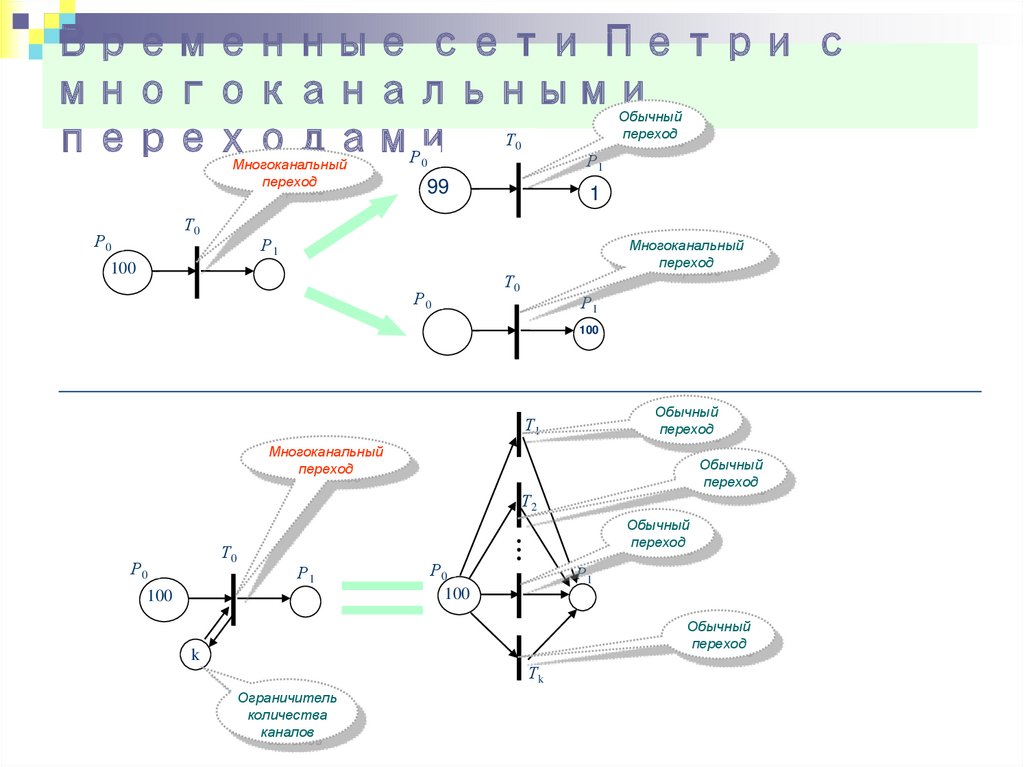
31. Временные сети Петри с многоканальными переходами

Временные сети Петри с
многоканальными
Т
переходами
Р
Р
Обычный
переход
0
Многоканальный
переход
Т0
Р0
0
1
99
1
Р1
Многоканальный
переход
100
Р0
Т0
Р1
100
Обычный
переход
Т1
Многоканальный
переход
Обычный
переход
Т2
Т0
Р0
Обычный
переход
Р1
100
Р0
100
Р1
Обычный
переход
k
Тk
Ограничитель
количества
каналов

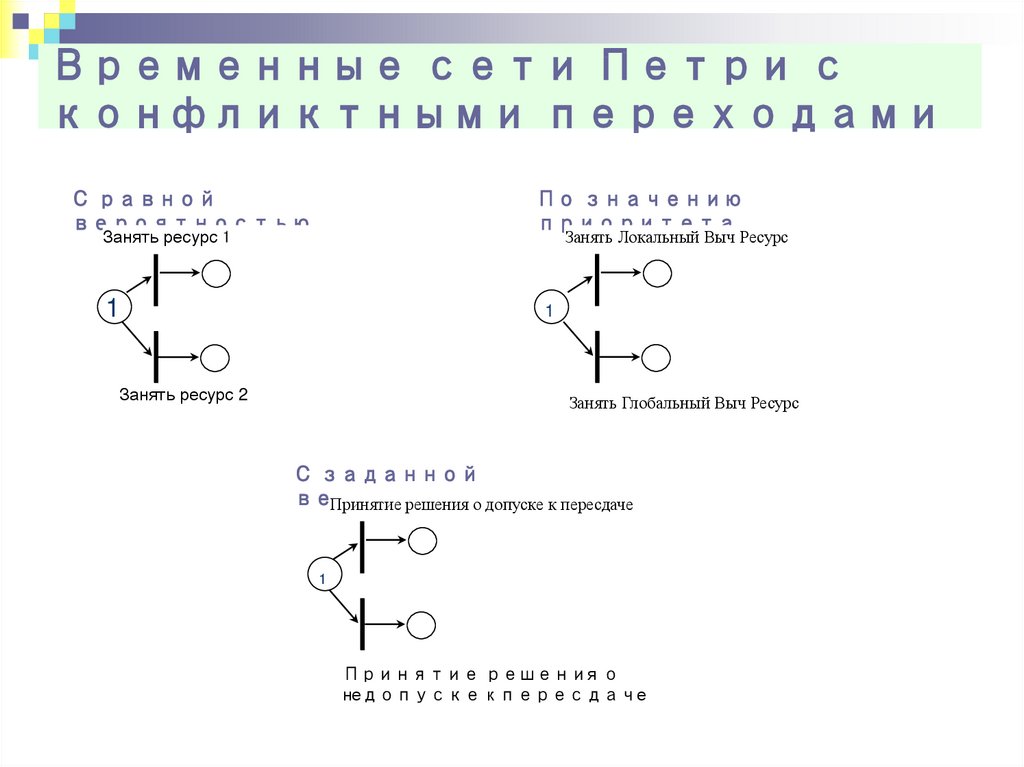
32. Временные сети Петри с конфликтными переходами

С равной
вероятностью
По значению
приоритета
Занять ресурс 1
Занять Локальный Выч Ресурс
1
1
Занять ресурс 2
Занять Глобальный Выч Ресурс
С заданной
вероятностью
Принятие решения о допуске к пересдаче
1
Принятие решения о
недопуске к пересдаче

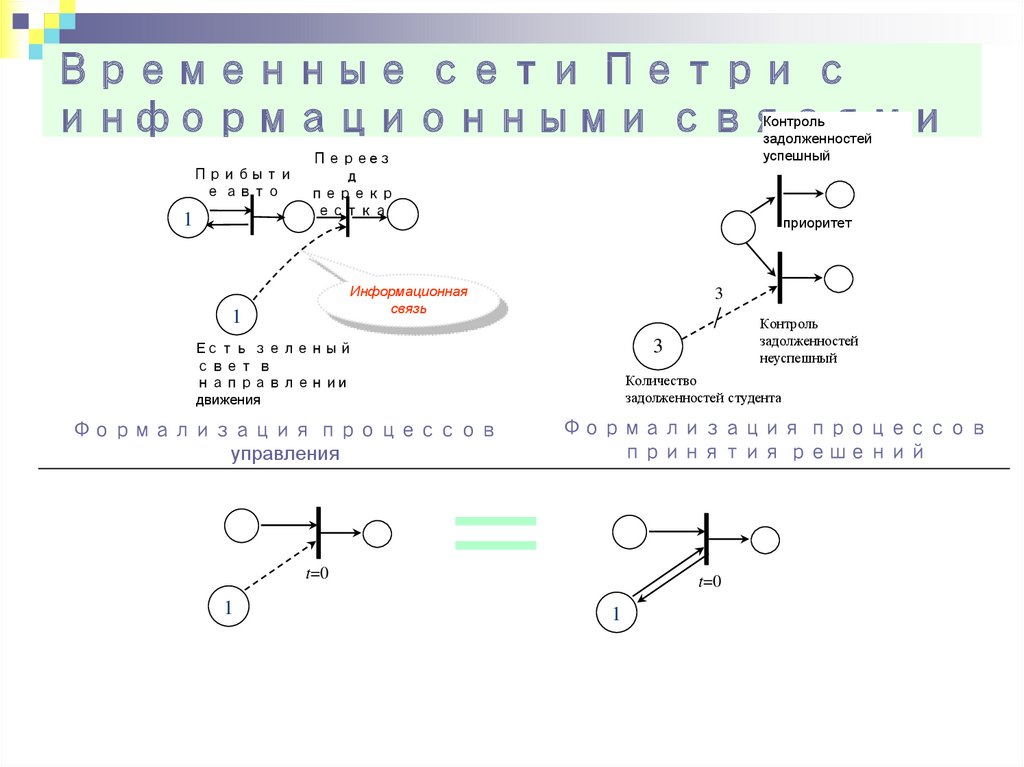
33. Временные сети Петри с информационными связями

Прибыти
е авто
1
Контроль
задолженностей
успешный
Переез
д
перекр
естка
приоритет
Информационная
связь
1
3
3
Есть зеленый
свет в
направлении
движения
Формализация процессов
управления
Количество
задолженностей студента
Формализация процессов
принятия решений
t=0
1
Контроль
задолженностей
неуспешный
t=0
1

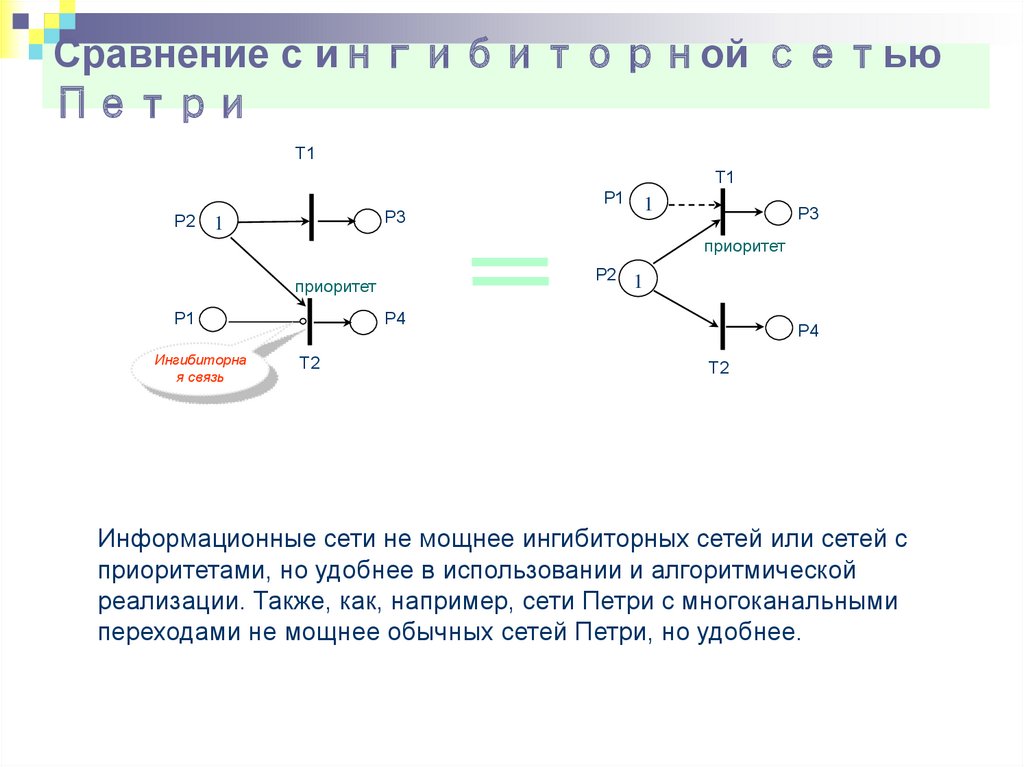
34. Сравнение с ингибиторной сетью Петри

Т1
Т1
Р1
Р2
Р3
1
1
Р3
приоритет
Р2 1
приоритет
Р1
Ингибиторна
я связь
Р4
Т2
Р4
Т2
Информационные сети не мощнее ингибиторных сетей или сетей с
приоритетами, но удобнее в использовании и алгоритмической
реализации. Также, как, например, сети Петри с многоканальными
переходами не мощнее обычных сетей Петри, но удобнее.

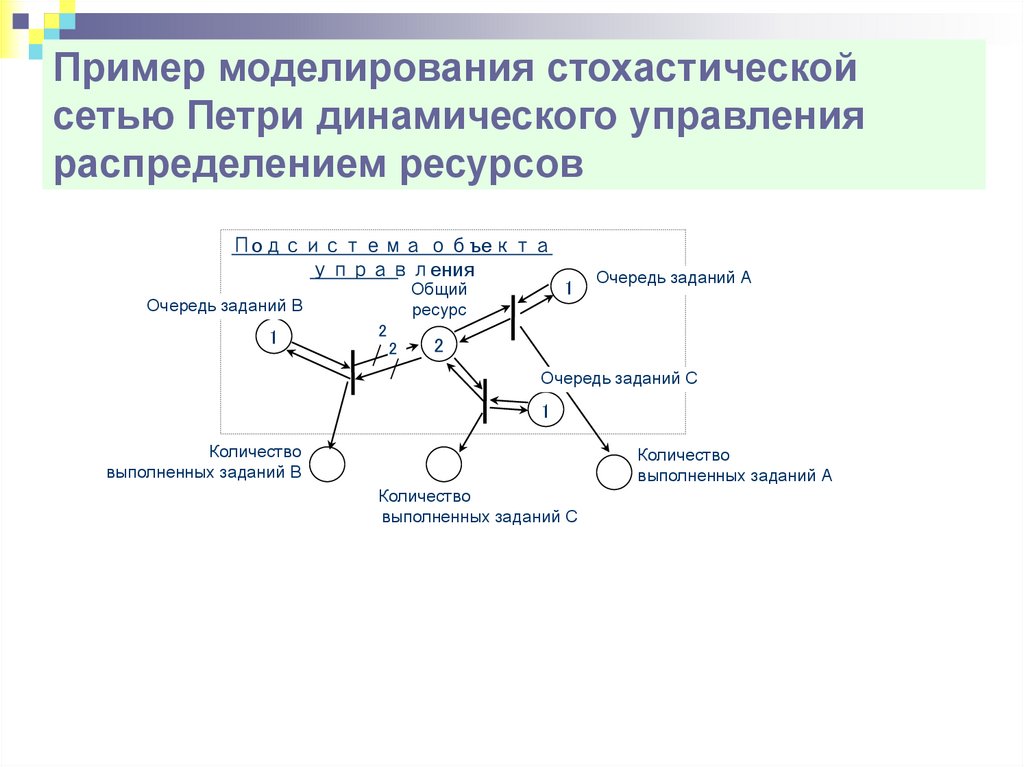
35.

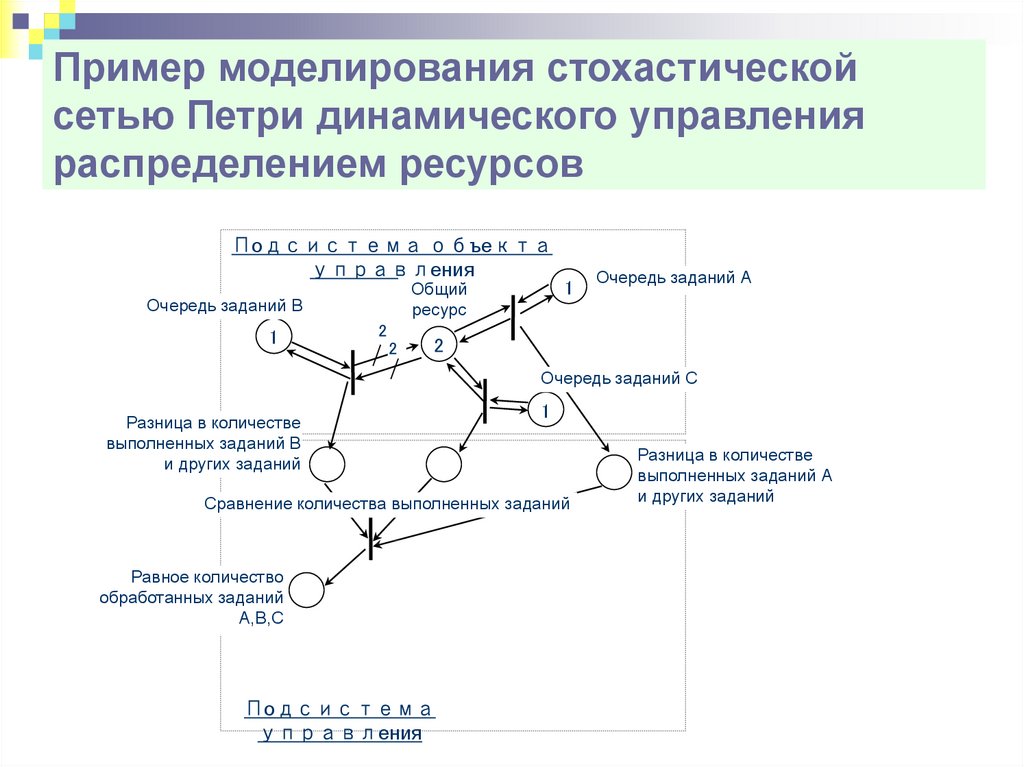
Пример моделирования стохастической
сетью Петри динамического управления
распределением ресурсов
Подсистема объекта
управления
Общий
ресурс
Очередь заданий В
1
2
2
1
Очередь заданий А
2
Очередь заданий С
1
Количество
выполненных заданий В
Количество
выполненных заданий А
Количество
выполненных заданий С

36.

Пример моделирования стохастической
сетью Петри динамического управления
распределением ресурсов
Подсистема объекта
управления
Общий
ресурс
Очередь заданий В
1
2
2
1
Очередь заданий А
2
Очередь заданий С
Разница в количестве
выполненных заданий В
и других заданий
1
Сравнение количества выполненных заданий
Равное количество
обработанных заданий
А,В,С
Подсистема
управления
Разница в количестве
выполненных заданий А
и других заданий

37.

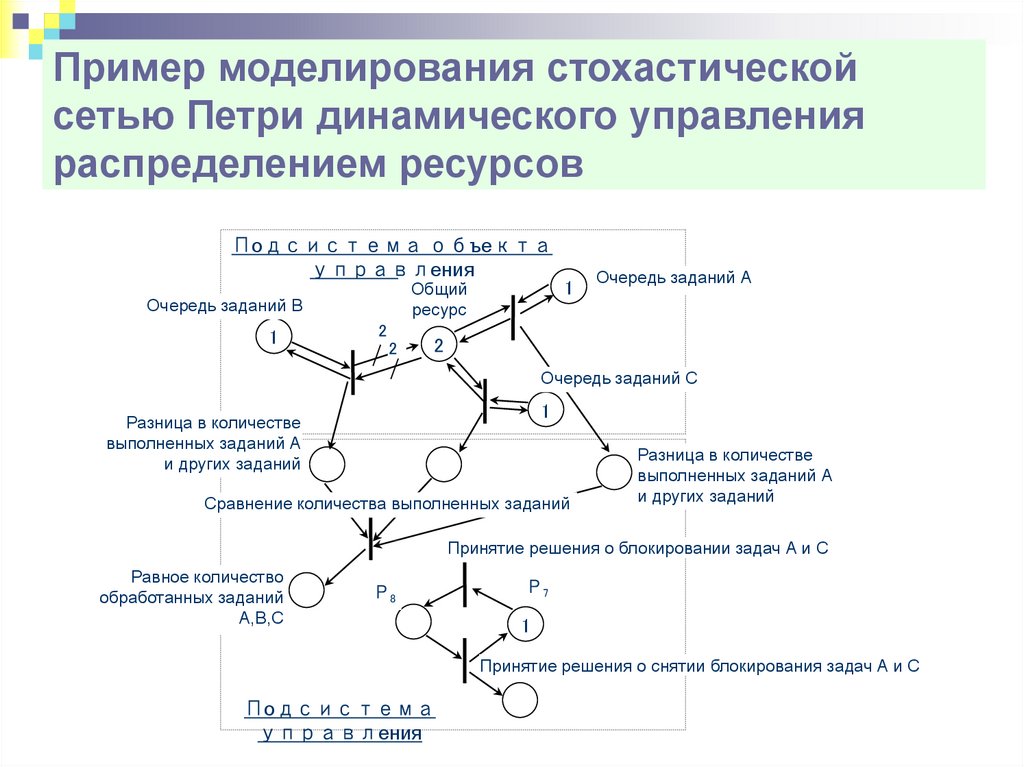
Пример моделирования стохастической
сетью Петри динамического управления
распределением ресурсов
Подсистема объекта
управления
Общий
ресурс
Очередь заданий В
1
2
2
1
Очередь заданий А
2
Очередь заданий С
1
Разница в количестве
выполненных заданий А
и других заданий
Сравнение количества выполненных заданий
Разница в количестве
выполненных заданий А
и других заданий
Принятие решения о блокировании задач А и С
Равное количество
обработанных заданий
А,В,С
Р8
Р7
1
Принятие решения о снятии блокирования задач А и С
Подсистема
управления

38.

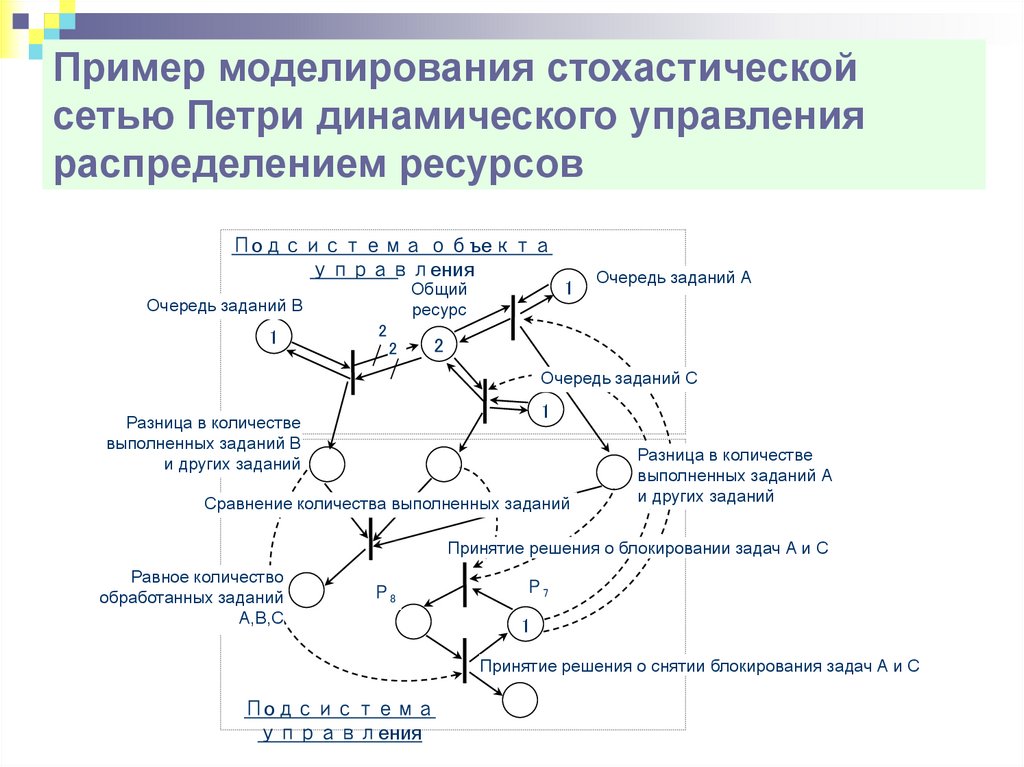
Пример моделирования стохастической
сетью Петри динамического управления
распределением ресурсов
Подсистема объекта
управления
Общий
ресурс
Очередь заданий В
1
2
2
1
Очередь заданий А
2
Очередь заданий С
1
Разница в количестве
выполненных заданий В
и других заданий
Сравнение количества выполненных заданий
Разница в количестве
выполненных заданий А
и других заданий
Принятие решения о блокировании задач А и С
Равное количество
обработанных заданий
А,В,С
Р8
Р7
1
Принятие решения о снятии блокирования задач А и С
Подсистема
управления

39. Уравнения состояний детерминированной временной сети Петри с конфликтными и многоканальными переходами

Уравнения состояний
детерминированной временной сети
Петри с конфликтными и
[Зайцев
Д.А. Инварианты временных
сетей Петри //
многоканальными
переходами
Кибернетика и системный анализ. – 2004. - №2. - С.92-106.]
Временная сеть Петри
S(n) (M(n), E(n))
- состояние
сети Петри
N ( P, T, A, W, R )
- временные
задержки
R:T
M P (n) M p (n 1) WT , P uT (n RT )
T P
M (n) M (n) W u n
P ,T T
P
P
T P
M P (n) 0, P P
,
v (n) & M (n) / W , P T
P ,T
P
T
0 uT (n) vT (n), T T
S (0) S 0 , n 1,2...
n – номер такта модельного времени
М p n - промежуточная маркировка, являющаяся результатом выхода маркеров из переходов
- количество каналов перехода T,
uT n
запущенных в такте n
vT n - количество каналов, для которых выполнено условие запуска в такте n

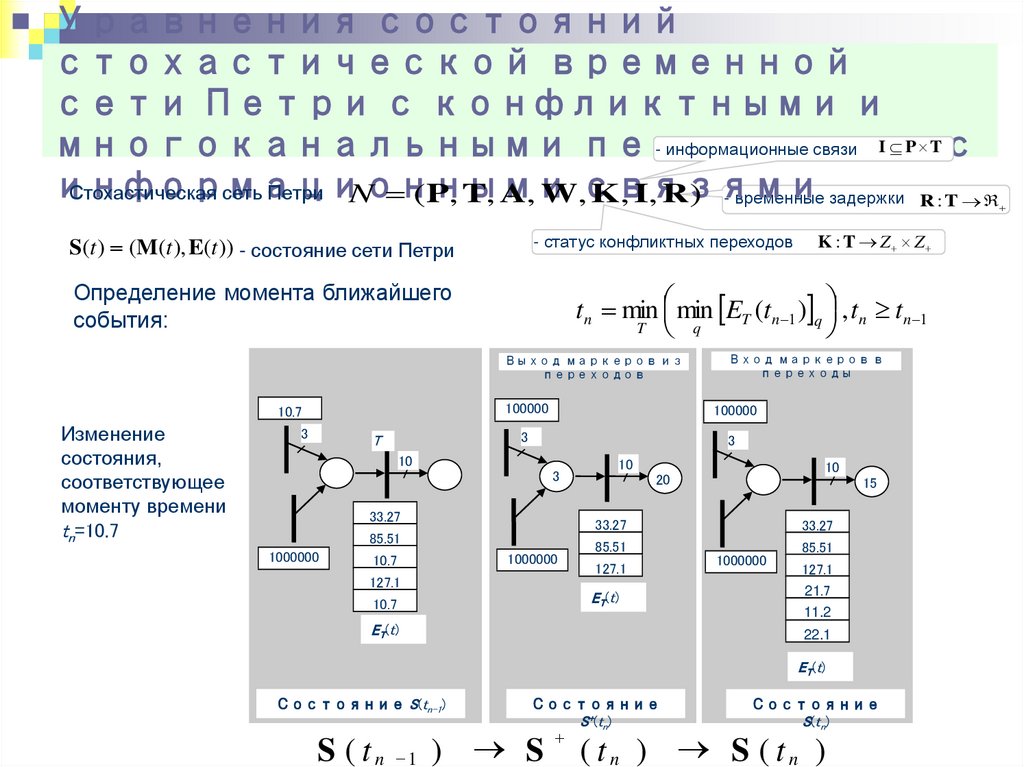
40. Уравнения состояний стохастической временной сети Петри с конфликтными и многоканальными переходами, с информационными связями

Уравнения состояний
стохастической временной
сети Петри с конфликтными и
- информационные связи I P Tс
многоканальными переходами,
информационными
Стохастическая сеть Петри N ( P, T, A, W,связями
K , I, R ) - временные задержки R : T
S(t ) (M(t ), E(t )) - состояние сети Петри
- статус конфликтных переходов
Определение момента ближайшего
события:
tn min min ET (tn 1 ) q , tn tn 1
T q
Выход маркеров из
переходов
10.7
Изменение
состояния,
соответствующее
моменту времени
tn=10.7
3
T
Вход маркеров в
переходы
100000
100000
3
3
10
3
33.27
10
10
20
15
33.27
85.51
1000000
1000000
10.7
K : T Z Z
127.1
85.51
127.1
ET(t)
10.7
ET(t)
33.27
1000000
85.51
127.1
21.7
11.2
22.1
ET(t)
Состояние S(tn-1)
S ( tn
1
Состояние
S+(tn)
) S
Состояние
S(tn)
( tn ) S ( tn )

41.

Преобразование сети Петри,
соответствующее
выходу
D : S(t n 1 ) S(t n )
маркеров из переходов
T T | Y (T , t n ) 1
if sT (tn 1 ) ET (t n 1 ) ,
E (t n )
ET (t n 1 ) \ ET (tn 1 ) q | q sT (tn 1 ) else
T
P P
Y (T , t n )
M P (tn ) M P (tn 1 )
Y (T , tn ) WT ,P | sT (tn 1 ) |
T P
- предикат, определяющий множество переходов,
для которых осуществляется выход маркеров в момент времени
min E (t ) t Y (T , t ) 1
T
n 1 q
n
n
q
min E (t ) t Y (T , t ) 0
T
n 1 q
n
n
q
sT (t )
- множество каналов перехода, которым соответствует
наименьший из всех моментов выхода маркеров из перехода
sT (t ) q | ET (t ) q min ET (t ) q
q

42.

Преобразование сети Петри,
соответствующее
входу
D : S(t n ) S(t n )
маркеров в переходы
P P
M P (tn ) M P (tn )
WP,T X (T , tn )
T P \ P
T T | X (T , t n ) 1
tn RT if min ET (tn 1 ) q ,
q
ET (tn )
ET (tn ) tn RT else
X (T , t n )
- предикат, определяющий множество переходов,
для которых осуществляется вход маркеров в момент времени
tn
T (t n ) X (T , t n ) 1,
T (t n ) X (T , t n ) 0.
(t n )
- подмножество множества переходов с выполненным условием запуска,
которое формируется в результате выбора из конфликтных переходов,
основывающегося на значениях приоритетов и вероятностей запуска переходов

43.

Преобразование сети Петри,
соответствующее m-кратному
входу маркеров в переходы
D
m
: S(t n ) S(t n )
m
m : D (S(t n )) :
M P (tn ) M P (tn )
P P
T Z (T , t n ) 0
WP,T uT (tn )
T P \ P
T T | X (T , t n ) 1
tn RT ... t n RT if min ET (t n 1 ) q ,
q
uT ( t n )
ET (t n )
t n RT ... t n RT else
ET (tn )
uT ( t n )
m
где uT (t n ) X (T , t n ) i - представляет количество входов маркеров в переход Т
i 1
в серии входов маркеров в переходы,
соответствующей моменту времени t n

44.

Уравнения состояний
стохастической временной
сети Петри с конфликтными и
многоканальными переходами, с
информационными
связями
t min (t ) , t t ,
n
T
T
S(t1 ) D
S(t n ) D
n 2,3...
n 1
n
n 1
S(t ) ,
D (S(t ) ,
где
T (t ) min ET (t ) q
m : D
Z (T , t n )
P T
P T
m
q
(S(t n )) :
m
0
m
n 1
- ближайший момент выхода маркеров из перехода
T Z (T , t n ) 0
- достигается состояние, при котором ни один из
переходов сети Петри не запускается
- предикат, определяющий множество переходов
с выполненным условием запуска в момент времени
M P (t n ) WP ,T Z (T , t n ) 1
M P (t n ) WP ,T Z (T , t n ) 0
tn

45.

Пример. Исследование параметров динамического
управления распределением ресурсов
Время выполнения задачи С = 1, задачи А =0,157, задачи В = 0,333.
Параметр «a» = кратность дуги, соединяющих позицию «Разница в количестве выполненных заданий А и
других заданий» и переход «Сравнение количества выполненных заданий» = кратность дуги, соединяющих
позицию «Разница в количестве выполненных заданий А и других заданий» и переход «Принятие решения о
блокировании задач А и С»
Параметр «b» = кратность дуги, соединяющих позицию «Разница в количестве выполненных заданий С и
других заданий» и переход «Сравнение количества выполненных заданий» = кратность дуги, соединяющих
позицию «Разница в количестве выполненных заданий С и других заданий» и переход «Принятие решения о
блокировании задач А и С»
Критерий =
сумма значений
«количество
выполненных заданий»
всех классов
a 1, b 2
Критерий =
сумма значений «разница в
количестве выполненных
заданий» всех классов
a 2, b 1
Критерий =
количество выполненных
заданий класса С
a 2, b 2

46. Матричные уравнения состояний стохастической временной сети Петри с конфликтными и многоканальными переходами, с

ET (t ) , T ,
информационными
связями
WT , P , T P
v (t )
a P ,T
0, T P
T
- количество активных каналов
перехода
n
WP ,T , T P \ P
0, T P \ P
a P ,T
0, T .
T (t n ) Z (T , t j ) uT (t j )
j 1
n
T (t n ) Y (T , t j ) | sT (t j 1 ) |
j 1
M(t ) M P (t )
v(t ) vT (t )
a aT , P
γ(t ) T (t )
a aT , P
η(t ) T (t )
- общее количество входов в переход
в течение всего интервала времени t 0 , t n
- общее количество выходов из перехода в течение всего
интервала времени
t 0 , t n
a a a
Введем матричную переменную
μ(t ) M(t ) a v(t )- вектор расширенной маркировки
μ(tn ) μ(t0 ) a γ(tn )
η(t n ) v(t n ) v(t 0 ) γ(t n )

47. Сравнение матричных уравнений состояний стохастической временной сети Петри с известными уравнениями состояний сети Петри

I
P
T (t n ) min T (t n ), ηT (t n )
Матричные уравнения состояний стохастической
временной сети Петри без информационных связей
- количество завершенных запусков перехода
v(tn ) v(t0 ),
η(tn ) γ(tn ) χ (tn )
μ M
RT 0 vT (t ) 0 μ(t ) M(t ), η(t n ) γ(t n )
M n M 0 AT x
M a χ (t n )
M(t n ) M(t 0 ) a a χ (t n )
Фундаментальное уравнение состояний базовой
сети Петри
RT const tn t0 n t
t 1, t 0 0 t n n
M(n) M(0) a a γ(n) a v(n) v(0)
M(n) M(0) a η(n) a γ(n)
M(n) M(0) a γ(n) v(n) v(0) a γ(n)
Фундаментальное уравнение состояний
детерминированной временной сети Петри

48.

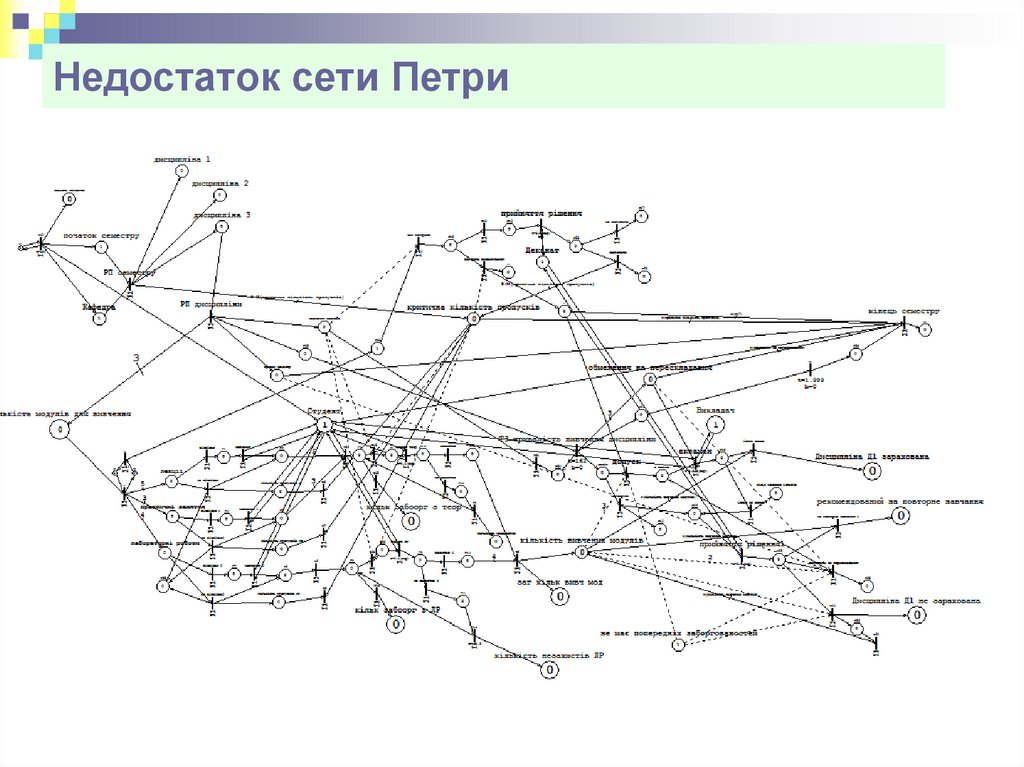
Недостаток сети Петри

49. ООП и сети Петри

“При проектировании сложной программной системы
необходимо составлять ее из небольших подсистем,
каждую из которых можно отладить независимо от других.”
Гради Буч
ООП и сети Петри
Блочная структура сети Петри
[Ямпольський Л.С., Лавров О.А. Штучний інтелект у плануванні та управлінні виробництвом. –
К.:Вища шк., 1995. - 255с. ]
[Стеценко І.В., Бойко О.В. Система імітаційного моделювання засобами сіток Петрі //
Математичні машини і системи. – Київ, 2009. – №1. – С.117-124. ]
Функциональные подсети
[Dmitriy A. Zaitsev Functional Petri net // Universite Paris Paris-Dauphine. - Cahier N 224. – mars
2005. – P.1-62.]
Объектно-ориентированные сети Петри
[Lakos C. Object Oriented Modeling with Object Petri Nets // Concurrent Object-Oriented Programming
and Petri Nets. - 2001. - P. 1-37. ]
[Lakos C., Keen C. LOOPN++: a new language for object-oriented Perti nets, Technical Report R94-4,
Networking Research Group, Univesity of Tasmania,Australia, April 1994.]
Иерархическая объектно-ориентированная сеть Петри
[Hue Xu Timed Hierarchical object-oriented Petri net // Petri Net, Theory and Applications, Book edited
by: Vedran Kordic. - I-Tech Education and Publishing, Vienna, Austria. - 2008. - P.253-280. ]
Высокоуровневые сети Петри для описания ООП
[Hong,J.E., Bae D.H. High-level Petri net for incremental specification of object-oriented system
requirements // Institution of Engineering and Technology, IEEE Proceedings – Software. - 2001. Vol. 148, No.1 - P.11-18. ]

50.

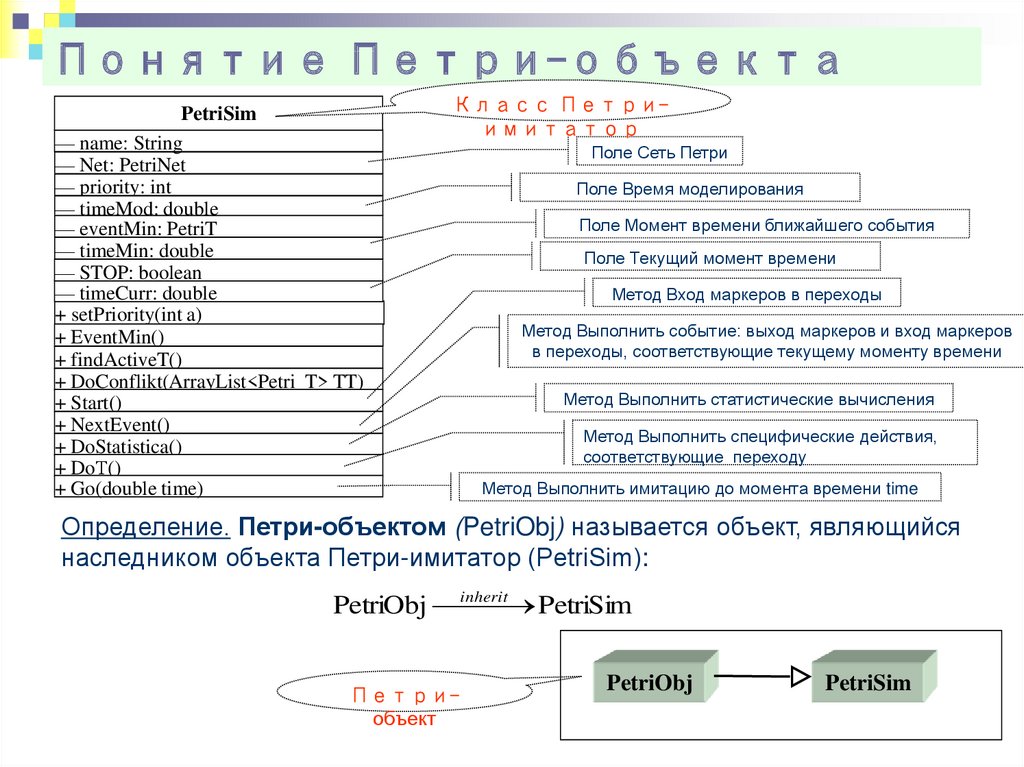
Понятие Петри-объекта
PetriSim
— name: String
— Net: PetriNet
— priority: int
— timeMod: double
— eventMin: PetriT
— timeMin: double
— STOP: boolean
— timeCurr: double
+ setPriority(int a)
+ EventMin()
+ findActiveT()
+ DoConflikt(ArrayList<Petri_T> TT)
+ Start()
+ NextEvent()
+ DoStatistica()
+ DoТ()
+ Go(double time)
Класс Петриимитатор
Поле Сеть Петри
Поле Время моделирования
Поле Момент времени ближайшего события
Поле Текущий момент времени
Метод Вход маркеров в переходы
Метод Выполнить событие: выход маркеров и вход маркеров
в переходы, соответствующие текущему моменту времени
Метод Выполнить статистические вычисления
Метод Выполнить специфические действия,
соответствующие переходу
Метод Выполнить имитацию до момента времени time
Определение. Петри-объектом (PetriObj) называется объект, являющийся
наследником объекта Петри-имитатор (PetriSim):
PetriObj inherit
PetriSim
Петриобъект
PetriObj
PetriSim

51.

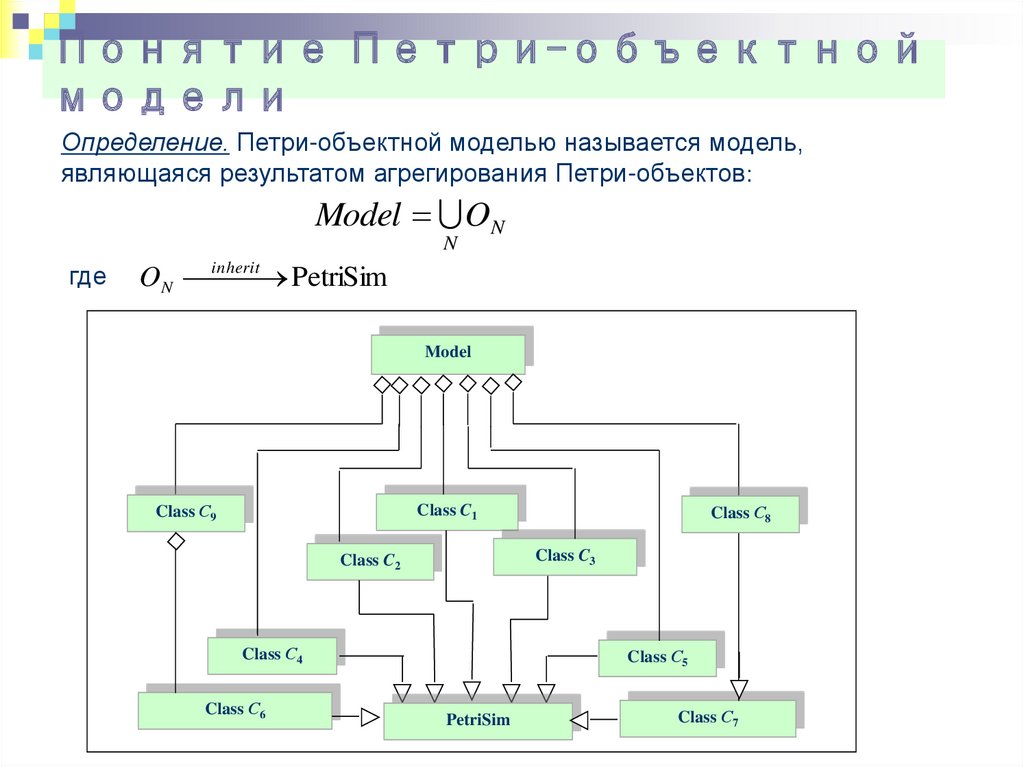
Понятие Петри-объектной
модели
Определение. Петри-объектной моделью называется модель,
являющаяся результатом агрегирования Петри-объектов:
Model ON
N
где
O N inherit
PetriSim
Model
Class С9
Class С8
Class C1
Class C3
Class C2
Class С4
Class С6
Class С5
PetriSim
Class С7

52.

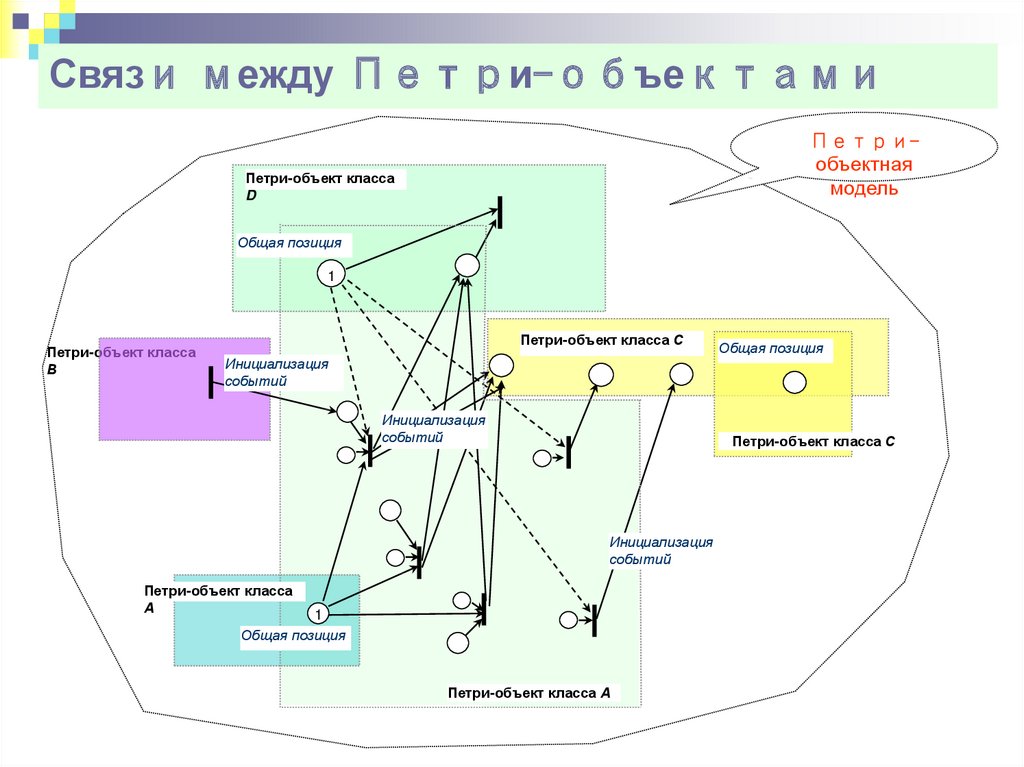
Связи между Петри-объектами
Петриобъектная
модель
Петри-объект класса
D
Общая позиция
1
Петри-объект класса
В
Петри-объект класса С
Общая позиция
Инициализация
событий
Инициализация
событий
Петри-объект класса С
Инициализация
событий
Петри-объект класса
А
1
Общая позиция
Петри-объект класса А

53.

Утверждение 1
Петри-объектная модель описывается
стохастической временной сетью
Петри, являющейся объединением сетей
Петри-объектов, из которых она
~
состоит:
ModelNet N
~
N
~ ~
~
N (TN , TN , A N , WN , K N , I N , R N )
где
~
~ N :
P TN
N
N
T TN
N
~
~
A AN
N
~
TN T P P | T T : (T , P) A N
T TN
~
AN AN UN
~
~
W WN
N
K K N
N
I IN
N
R RN
N
~
WN WN w N
U N (T , P) | T Tk , P Pl , wk ,l 0 - множество дуг Петри- объекта, соединяющих его с другими
объектами посредством инициализации событий
Следствие. Петри-объектная модель
является вычислимой.

54.

Утверждение 2
Преобразование D
~
сети Петри-объектной модели
N
~
эквивалентно преобразованию
D
N
сетей Петри-объектов
~ ~
~
N (TN , TN , A N , WN , K N , I N , R N )
Следствие. Состояние Петри-объектной
модели, являющееся результатом выхода
маркеров из переходов сети Петриобъектной модели, описывается
состоянием ее Петри-объектов:
~
~
D (S1 (t n 1 )) S1 (t n )
...
...
~
~
S (t n ) D S(t n 1 ) D (S N (t n 1 )) S N (t n )
...
...
~
~
D (S L (t n 1 )) S L (t n )

55.

Утверждение 3
Преобразование D
~
N
сети Петри-объектной
модели
~
N
эквивалентно преобразованию D
сетей Петри-объектов
~ ~
~
N (TN , TN , A N , WN , K N , I N , R N ),
для которых в случае существования общих позиций Петриобъектов решен конфликт
Следствие. Состояние Петри-объектной
модели, являющееся результатом входа
маркеров в переходы сети Петриобъектной модели, описывается
состоянием ее Петри-объектов.
~
~
D (S
(t n )) S1 (t n )
1
...
...
~
~
S(t n ) D S (t n ) D (S N (t n )) S N (t n )
...
...
~
~
D (S L (t n ))) S L (t n )

56.

Уравнения состояний Петри-объектной
модели
Следствие. Состояние Петри-объектной модели в каждый момент
времени описывается состоянием ее Петри-объектов.
S(t n ) D
m
~
~
D (S1 (t n 1 )) D m D (S
1 (t n 1 ))
...
...
m
m ~
~
D (S(t n 1 )) D D (S N (t n 1 )) D
D (S N (t n 1 ))
...
...
~
m ~
D (S L (t n 1 ))
D (S L (t n 1 )) D
Уравнения состояний Петри-объектной модели
t n min N , tn t n 1
N
D
D
S(t n ) D
D
m
m
m
~
(S1 (t n 1 ))
...
~
D (S N (t n 1 ))
...
~
D (S L (t n 1 ))
D m S (t )
1 0
...
m
S(t1 ) D S N (t0 )
...
m
D
S
(
t
)
L 0
~
S N (t n ) :
T TN
Z (T , t n ) 0

57. Алгоритм имитации Петри-объектной модели

Алгоритм имитации Петриобъектной модели
Формировать список Петри-объектов;
m
Осуществить преобразование D
(метод Start());
Пока не достигнут момент окончания моделирования
продвинуть время в момент ближайшего события;
определить список конфликтных объектов и выбрать объект из
списка конфликтных объектов;
m
для выбранного объекта выполнить преобразование D D
(методы NextEvent(), DoT()) ;
m
для всех других объектов осуществить преобразование D
(метод Start());
Вывести результаты моделирования.
Анализ вычислительной сложности алгоритма:
O T V timeMod mean T V V T mean T V 2 T V K 2
2
T T
Среднее количество
активных каналов перехода
T T
Среднее количество
конфликтных переходов

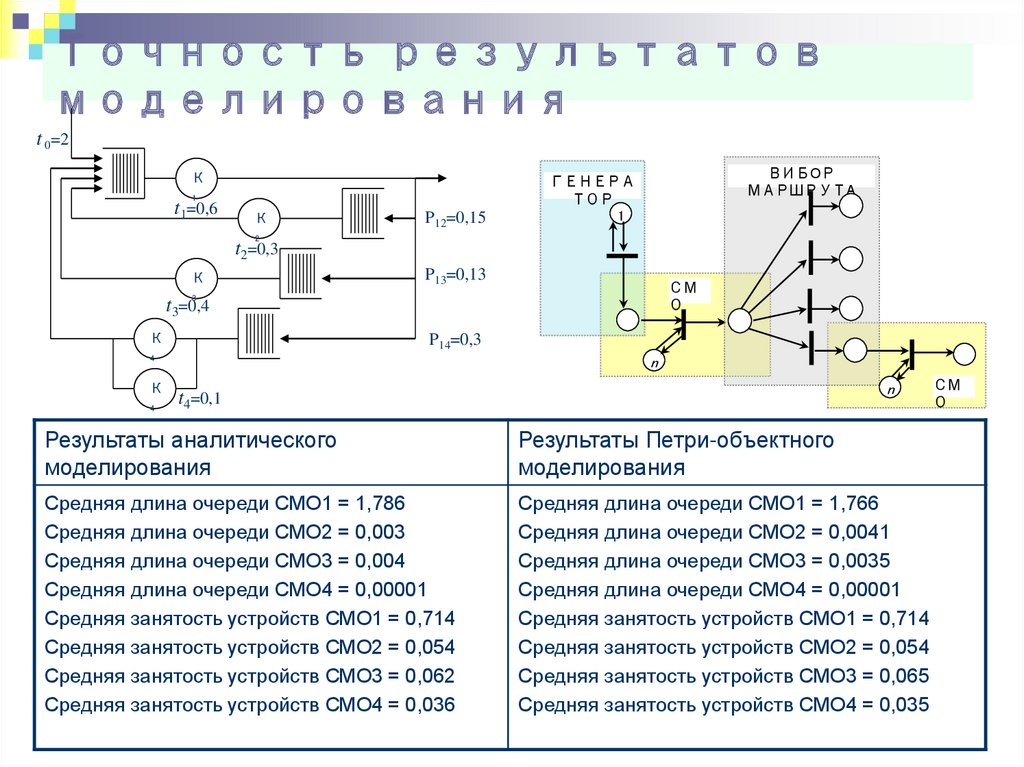
58. Точность результатов моделирования

t 0=2
К
1
t1=0,6
К
P12=0,15
ВИБОР
МАРШРУТА
ГЕНЕРА
ТОР
1
2
t2=0,3
К
P13=0,13
СМ
О
3
t3=0,4
К
P14=0,3
4
К
4
n
n
t4=0,1
Результаты аналитического
моделирования
Результаты Петри-объектного
моделирования
Средняя длина очереди СМО1 = 1,786
Средняя длина очереди СМО2 = 0,003
Средняя длина очереди СМО3 = 0,004
Средняя длина очереди СМО4 = 0,00001
Средняя занятость устройств СМО1 = 0,714
Средняя занятость устройств СМО2 = 0,054
Средняя занятость устройств СМО3 = 0,062
Средняя занятость устройств СМО4 = 0,036
Средняя длина очереди СМО1 = 1,766
Средняя длина очереди СМО2 = 0,0041
Средняя длина очереди СМО3 = 0,0035
Средняя длина очереди СМО4 = 0,00001
Средняя занятость устройств СМО1 = 0,714
Средняя занятость устройств СМО2 = 0,054
Средняя занятость устройств СМО3 = 0,065
Средняя занятость устройств СМО4 = 0,035
СМ
О

59.

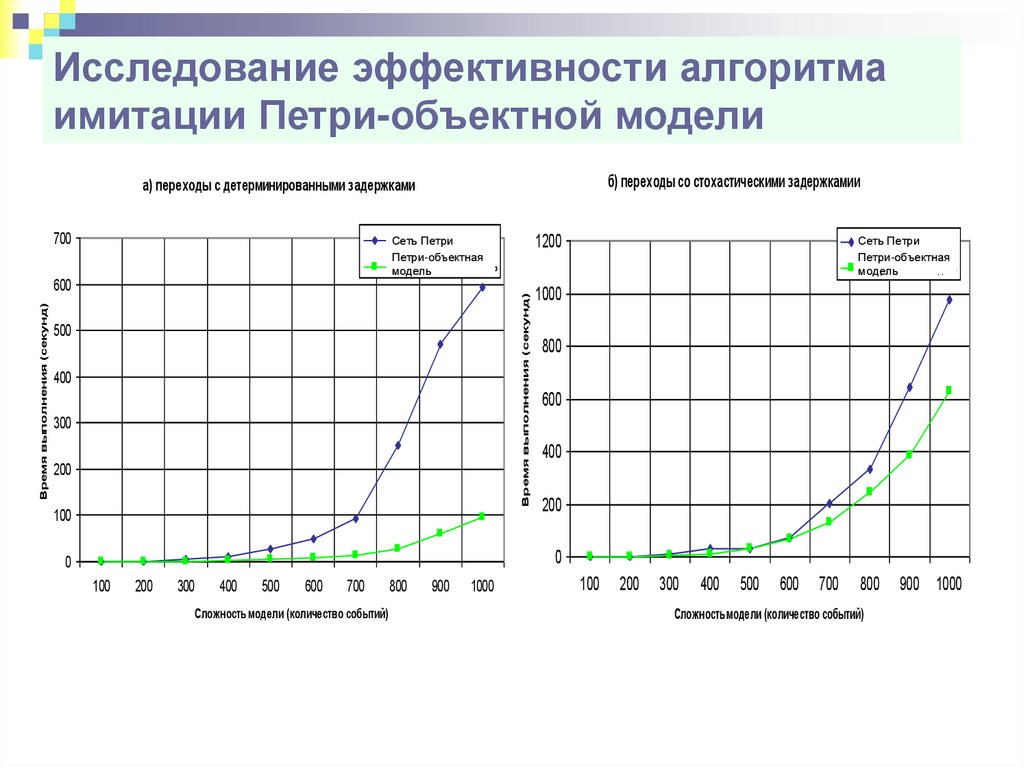
Исследование эффективности алгоритма
имитации Петри-объектной модели
б) переходы со стохастическими задержкамии
а) переходы с детерминированными задержками
700
Петри-объектная
Петрі-об'єктна
модель
модель
Время выполнения (секунд)
600
Время выполнения (секунд)
1200
Сеть Петри
Мережа
Петрі
500
400
300
200
100
Сеть
Петри
Мережа
Петрі
Петри-объектная
Петрі-об'єктна модель
модель
1000
800
600
400
200
0
0
100
200
300
400
500
600
700
Сложность модели (количество событий)
800
900
1000
100
200
300
400
500
600
700
800
Сложность модели (количество событий)
900 1000

60.

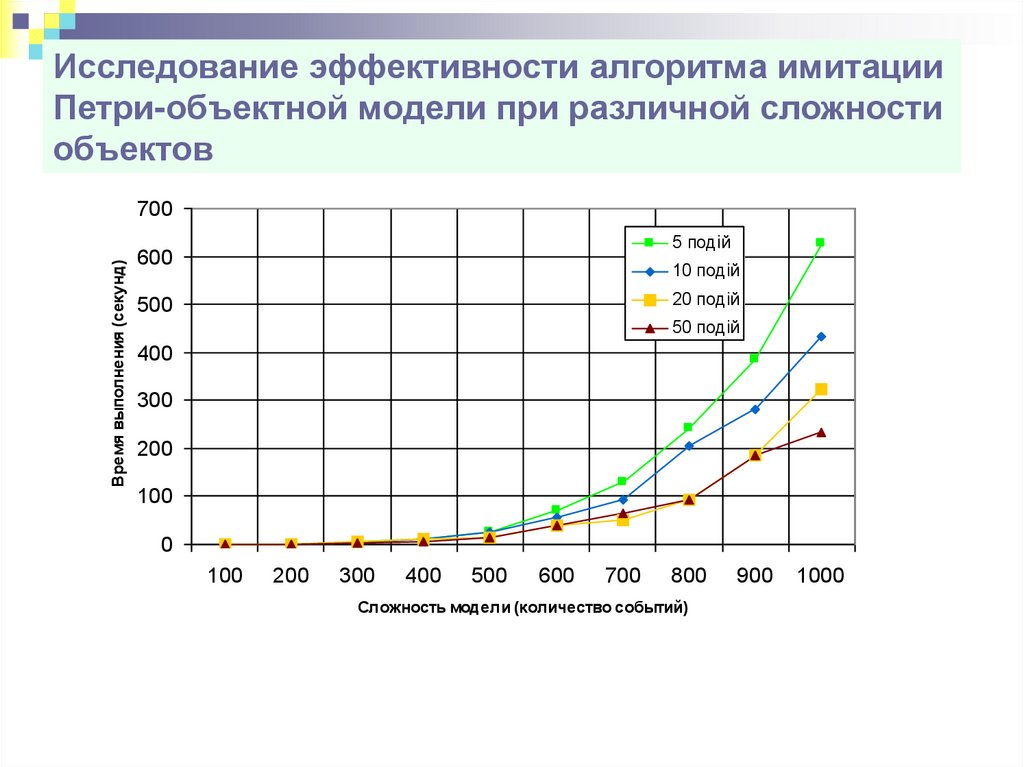
Исследование эффективности алгоритма имитации
Петри-объектной модели при различной сложности
объектов
Время выполнения (секунд)
700
5 подій
600
10 подій
20 подій
500
50 подій
400
300
200
100
0
100
200
300
400
500
600
700
800
Сложность модели (количество событий)
900
1000

61. Петри-объектная модель

- это средство формального описания
систем, которое:
1) имеет математическое описание, а
следовательно, имеет большую степень
абстракции и наиболее
формализованное описание алгоритма
имитации;
2) допускает не только имитационные
методы исследования, но и
аналитические методы;
3) позволяет создавать модели больших и
сложных систем с наименьшими
затратами времени и труда;
4) основывается на временной
стохастической сети Петри, а значит,
допускает наиболее детализированное

62. Практическое применение Петри-объектного моделирования

• Моделирование систем управления (учебный процесс,
транспортные системы)
• Моделирование параллельных вычислений (грид-системы)
• Моделирование процессов управления организациями и
предприятиями (процессно-ориентированный подход к
управлению)
• Распределенное моделирование (модель большой системы
строится с участием коллектива разработчиков). Это идея и
концепция, которой придерживались при разработке ООП
• Петри-процессор (Петри-машина) и «новая парадигма
вычислений»

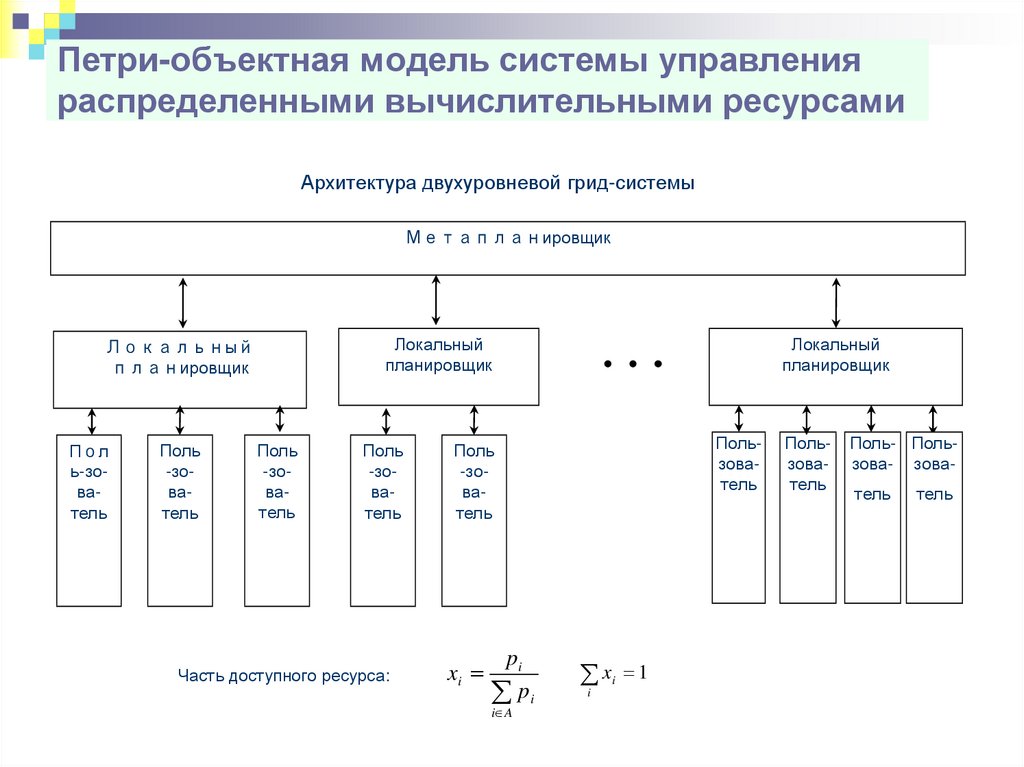
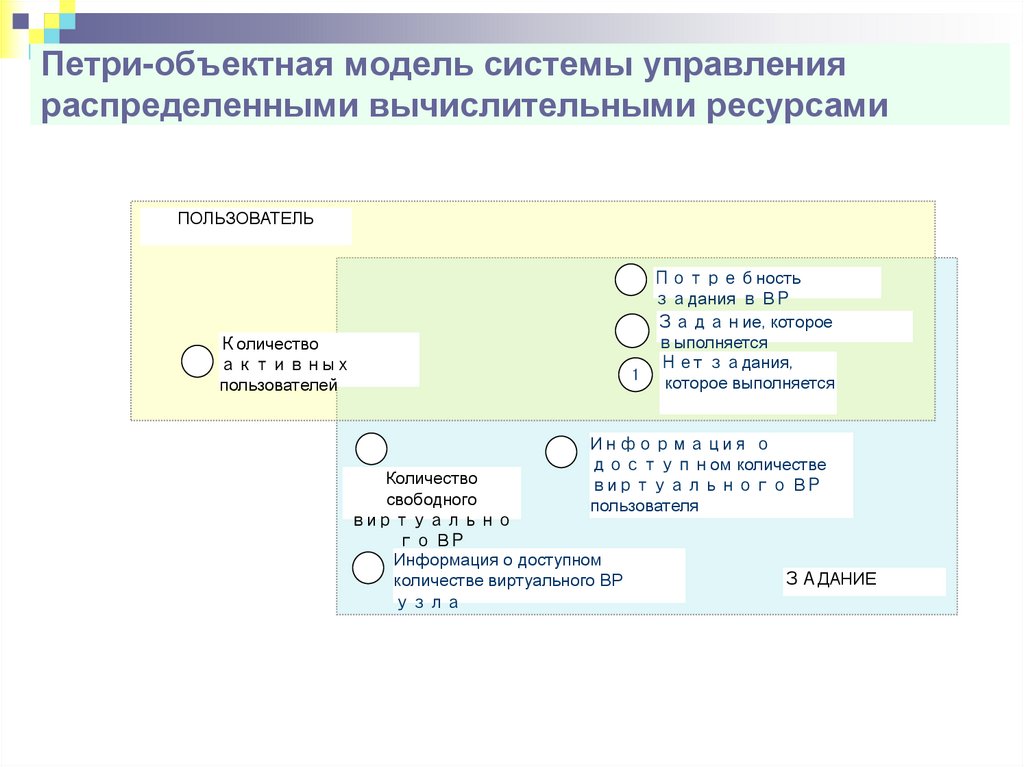
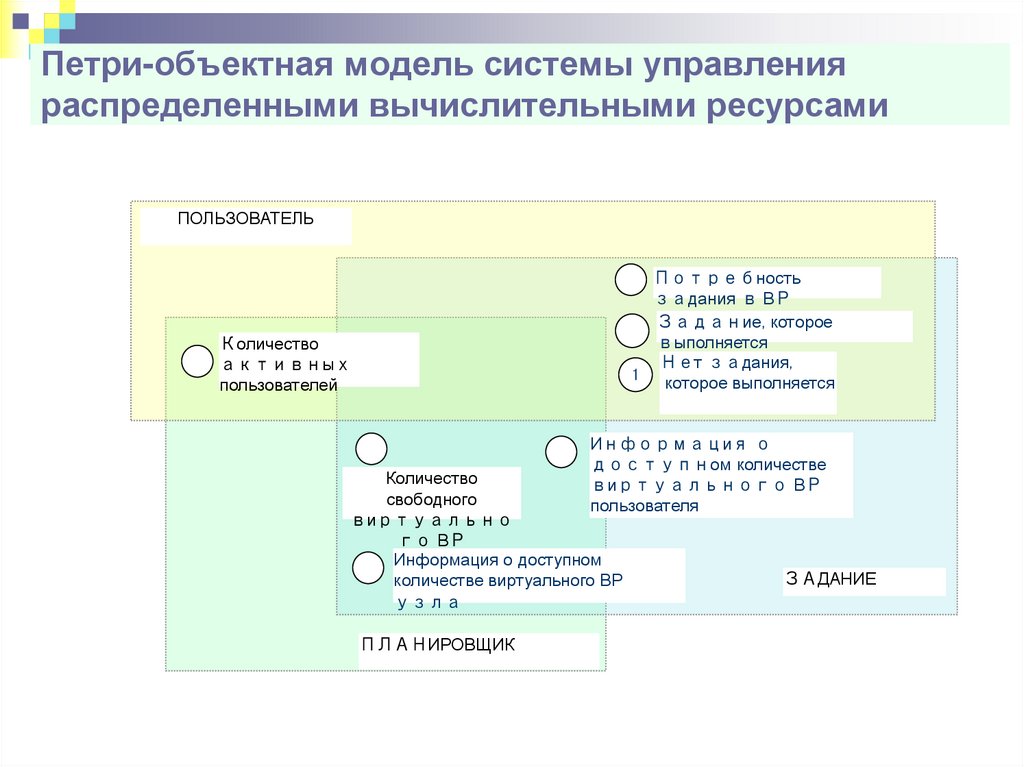
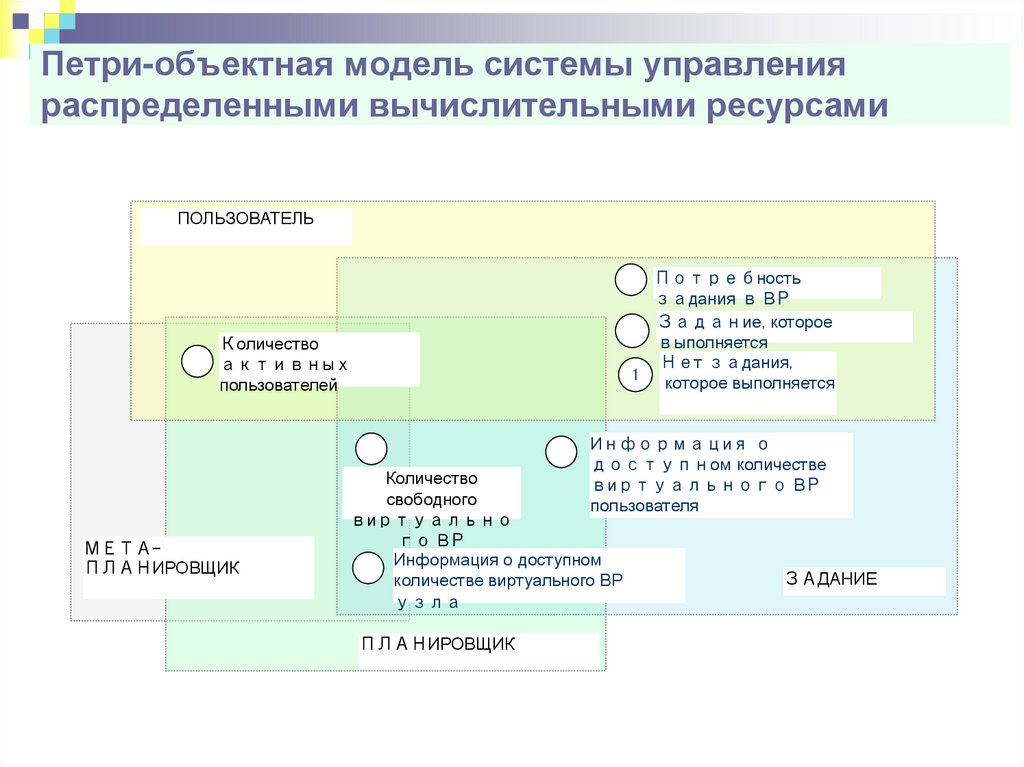
63. Петри-объектная модель системы управления распределенными вычислительными ресурсами

Архитектура двухуровневой грид-системы
Метапланировщик
Локальный
планировщик
Локальный
планировщик
Пол
ь-зователь
Поль
-зователь
Поль
-зователь
Поль
-зователь
Часть доступного ресурса:
Локальный
планировщик
Пользователь
Поль
-зователь
xi
pi
pi
i A
xi
i
1
Пользователь
Поль- Пользова- зователь
тель

64. Петри-объектная модель системы управления распределенными вычислительными ресурсами

ПОЛЬЗОВАТЕЛЬ А
Количество
активных
пользователей
Потребность
задания в ВР
Задание, которое
выполняется
Нет задания,
1 которое выполняется

65. Петри-объектная модель системы управления распределенными вычислительными ресурсами

ПОЛЬЗОВАТЕЛЬ
Потребность
задания в ВР
Задание, которое
выполняется
Нет задания,
1 которое выполняется
Количество
активных
пользователей
Информация о
доступном количестве
виртуального ВР
пользователя
Количество
свободного
виртуально
го ВР
Информация о доступном
количестве виртуального ВР
узла
ЗАДАНИЕ

66. Петри-объектная модель системы управления распределенными вычислительными ресурсами

ПОЛЬЗОВАТЕЛЬ
Потребность
задания в ВР
Задание, которое
выполняется
Нет задания,
1 которое выполняется
Количество
активных
пользователей
Информация о
доступном количестве
виртуального ВР
пользователя
Количество
свободного
виртуально
го ВР
Информация о доступном
количестве виртуального ВР
узла
ПЛАНИРОВЩИК
ЗАДАНИЕ

67. Петри-объектная модель системы управления распределенными вычислительными ресурсами

ПОЛЬЗОВАТЕЛЬ
Потребность
задания в ВР
Задание, которое
выполняется
Нет задания,
1 которое выполняется
Количество
активных
пользователей
Информация о
доступном количестве
виртуального ВР
пользователя
МЕТАПЛАНИРОВЩИК
Количество
свободного
виртуально
го ВР
Информация о доступном
количестве виртуального ВР
узла
ПЛАНИРОВЩИК
ЗАДАНИЕ

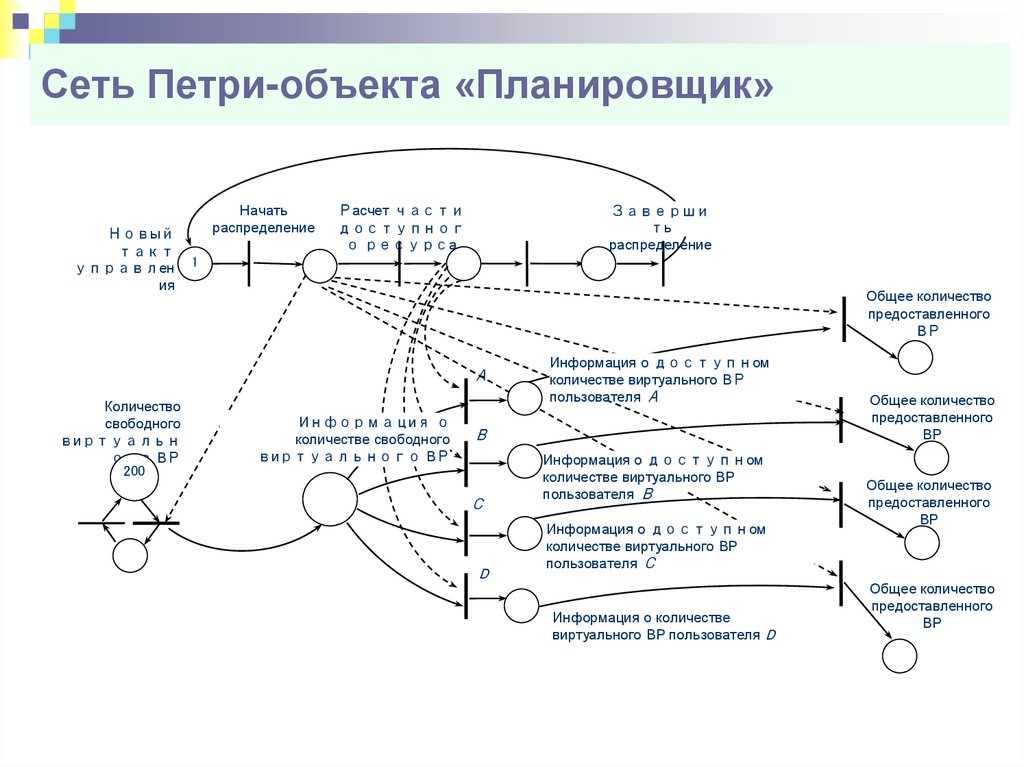
68. Сеть Петри-объекта «Планировщик»

Новый
такт
управлен
ия
Начать
распределение
Расчет части
доступног
о ресурса
Заверши
ть
распределение
1
Общее количество
предоставленного
ВР
А
Количество
свободного
виртуальн
ого ВР
200
Информация о
количестве свободного
виртуального ВР
Информация о доступном
количестве виртуального ВР
пользователя А
В
С
D
Информация о доступном
количестве виртуального ВР
пользователя В
Информация о доступном
количестве виртуального ВР
пользователя С
Информация о количестве
виртуального ВР пользователя D
Общее количество
предоставленного
ВР
Общее количество
предоставленного
ВР
Общее количество
предоставленного
ВР

69.

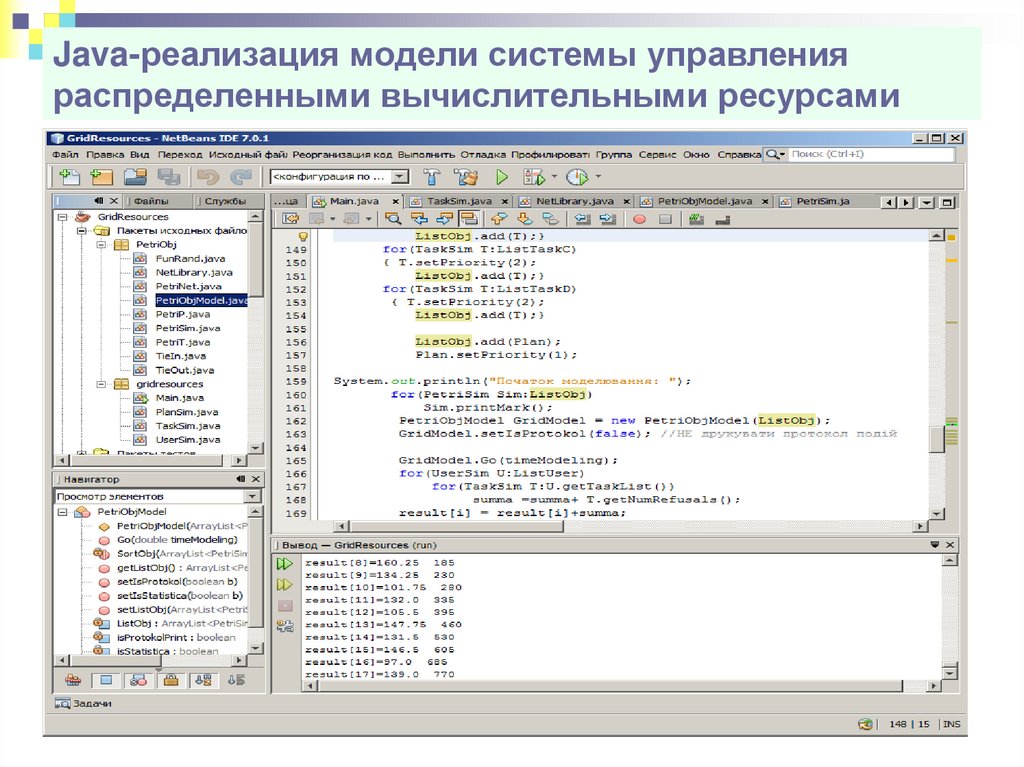
Java-реализация модели системы управления
распределенными вычислительными ресурсами

70.

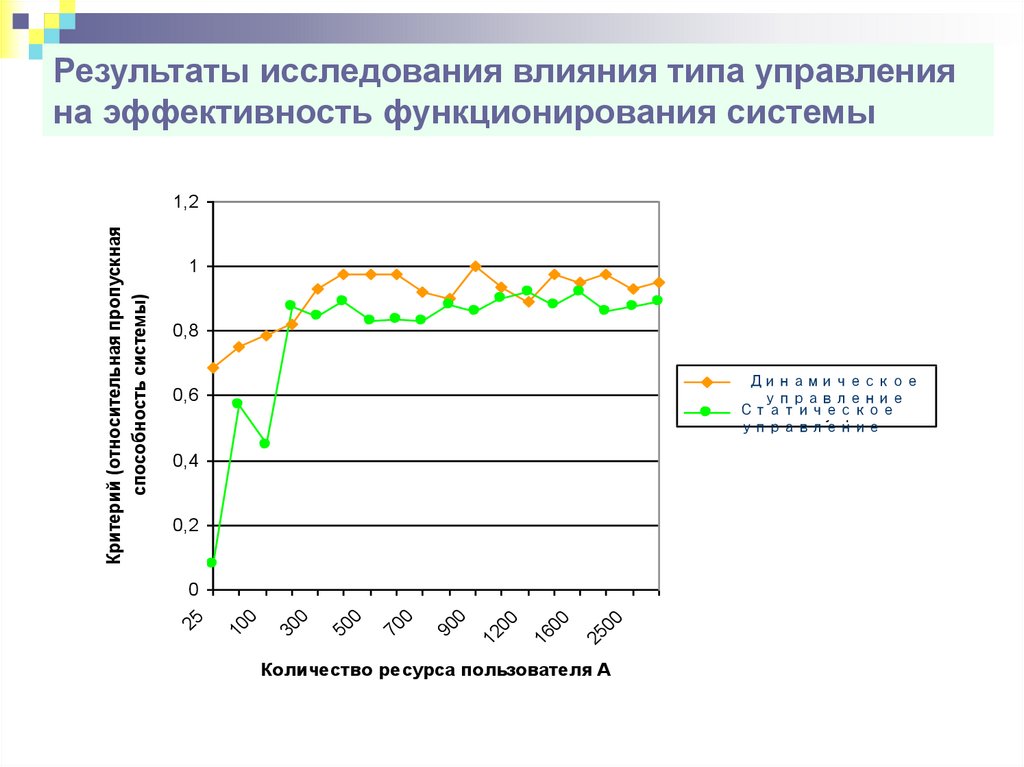
Результаты исследования влияния типа управления
на эффективность функционирования системы
1
0,8
Динамическое
Динамічне
управ ління
0,6
управление
Статическое
Статичне
управ ління
управление
0,4
0,2
25
00
16
00
12
00
90
0
70
0
50
0
30
0
10
0
0
25
Критерий (относительная пропускная
способность системы)
1,2
Количество ресурса пользователя А

71. Заключение

Разработаны теоретические основы новой
технологии моделирования систем,
объединяющей в себе объектно-ориентированную технологию
и технологию имитационного моделирования
стохастической сетью Петри.
Эффективность Петри-объектной технологии обеспечивается
сокращением затрат труда на
алгоритмическую реализацию
модели системы и значительным повышением
скорости вычислений модели.
Формализация средствами Петриобъектного моделирования
является мощным инструментом
исследования сложных дискретнособытийных систем
Дальнейшие исследования связаны
с
усовершенствованием библиотеки Javaклассов Петри-объектного
моделирования;
разработкой графического
интерфейса ввода сетей Петриобъектов;

72. Спасибо за внимание!