ВПМ. Математичне програмування та дослідження операцій. Динамічне програмування. Задача заміни устаткування. (Лекція 6)

1. Вища та прикладна математика Модуль: Математичне програмування та дослідження операцій

Вища та
прикладна
математика
Університет митної справи та фінансів
Модуль: Математичне
програмування та
дослідження операцій
доц. Лебідь О.Ю.
Дніпропетровськ
2016

2. Тема 11: Динамічне програмування. Задача заміни устаткування

План
1. Динамічне програмування
2. Принцип оптимальності Беллмана
3. Загальна постановка динамічної задачі
програмування
4. Принципи підходу до розв'язування ЗДП
5. Реалізація моделей ДП
6. Задачі динамічного програмування
7. Труднощі у динамічному програмуванні
8. Задача заміни
9. Задача про заміну устаткування
10. Геометричне рішення задачі заміни 2

3. Динамічне програмування

У задачах лінійного і нелінійного програмування
етап планування не розбивається на окремі етапи
(кроки) і оптимальний план визначається для всього
періоду планування (доба, тиждень, рік і таке ін.). Ці
методи
одержали
назву
одноетапних
або
однокрокових. Математичні моделі в цьому випадку
статичні й не враховують зміну параметрів у часі.
3

4. Динамічне програмування

Будь-яку багатоетапну задачу можна розв’язувати
двома способами: шукати оптимальний розв’язок
відразу або будувати його крок за кроком.
Другий спосіб простіший. Його суть у поступовій,
поетапній оптимізації, що особливо важливо в
задачах, де ситуація змінюється в часі.
4

5. Динамічне програмування

У реальних системах потрібно знаходити і
приймати оптимальні рішення на кожному етапі й
одночасно на всьому розглянутому процесі в цілому
з урахуванням можливих змін параметрів. Такі
задачі називають багатоетапними (багатокроковими), а математичний апарат, за допомогою якого
знаходять
відповідний
розв’язок,
називають
динамічним
програмуванням
(динамічним
плануванням). Сукупність рішень, прийнятих на
кожному етапі з урахуванням стану системи і
цільової функції, називають керуванням.
5

6. Динамічне програмування

Динамічне програмування – це оптимальне
керування на кожному кроці з урахуванням
одночасного забезпечення оптимального керування
об’єктом
(процесом)
протягом
усього
багатокрокового періоду, тобто на кожному кроці
треба вибирати керування з урахуванням його
майбутніх наслідків на ще майбутніх кроках. Але є
виняток з цього правила. Останній крок треба
планувати так, щоб він приносив найбільшу вигоду.
6

7. Динамічне програмування

Розподіл на кроки (етапи) вводиться штучно.
Наприклад, процес виведення космічного корабля
на орбіту або рух потяга можна умовно розбити на
етапи за часом, для визначення оптимальної
конструкції балки її довжину поділяють на відрізки
певної довжини і таке ін.
Оскільки весь період планування поділяється на
етапи, то й функція мети визначається в результаті
підсумовування її складових, одержуваних на
окремих етапах, тобто виграш за весь період
планування дорівнює сумі виграшів на всіх етапах.
7

8. Динамічне програмування

Динамічна модель у прискореному режимі
дозволяє
досліджувати
розвиток
складної
економічної
системи, скажімо, підприємства,
протягом певного періоду планування в умовах
зміни ресурсного забезпечення (сировини, кадрів,
фінансів, техніки), і дозволяє одержані результати
представити у відповідному плані розвитку
підприємства на заданий плановий період.
8

9. Принцип оптимальності Беллмана

Принцип
оптимальності
динамічного
програмування
сформулював
Р. Беллман:
«Оптимальна поведінка має таку властивість: які б
не були первісний стан і рішення в початковий
момент,
наступні
рішення
повинні
бути
оптимальними щодо стану, отриманого в результаті
первісного рішення».
9

10. Загальна постановка динамічної задачі програмування

У загальному випадку задача динамічного
програмування може бути сформульована в такий
спосіб: деяка фізична або економічна система в
початковий момент часу T0 знаходиться в станi S0.
Цей стан визначається n-вимірним вектором
параметрів системи. За період часу T0–Tk система має
бути переведена в деякий кінцевий стан Sk,
обумовлений відповідними значеннями вектора
станів.
10

11. Загальна постановка динамічної задачі програмування

Перехід здійснюється за скінченну кількість
кроків, на кожному з яких система переводиться в
деякий проміжний стан Sі. При цьому необхідно
забезпечити оптимальне значення критерію, що
оцінює якість керування, або процес переходу від S0
до Sk. Перехід системи зі стану в стан
характеризується набором послідовних станів S0, S1,
… Sі, …..., Sk, що називається траєкторією руху
системи.
11

12. Загальна постановка динамічної задачі програмування

Перехід системи забезпечується за допомогою
ряду послідовних керуючих впливів, або керувань
ui. Сукупність керувань ui позначимо через U. Тоді
задача динамічного програмування полягає у виборі
оптимального керування U, що послідовно
переводить систему зі стану в стан від S0 до Sk за
умови, що критерій F(U) набуває екстремального
значення
F opt[ F (U )].
U
12

13. Принципи підходу до розв’язування динамічних задач програмування

Принципи підходу до розв’язування задач динамічного програмування містять два припущення:
1. Оптимальне керування процесом на кожному кроці
визначають на основі того стану, якого система досягла
до початку цього кроку (принцип оптимальності
Р. Беллмана).
2. Критерій, за допомогою якого визначається
оптимальне керування на кожному кроці і для всього
процесу в цілому, має властивість адитивності, тобто
виграш або втрати на кожному кроці накопичуються на
серії кроків підсумовуванням
критерію на і-му кроці.
k
F Fi ,
i
де Fi – значення
13

14. Реалізація моделей динамічного програмування

Реалізація моделей динамічного програмування
відрізняється однією особливістю: з усіх можливих
станів системи фактично точно відомі тільки два S0 і
Sk, а приймати рішення необхідно для кожного
кроку. При цьому потрібно враховувати розвиток
процесу до цього кроку і після нього, що породжує
основні труднощі при виборі оптимального
керування; невідомо, як реально буде розвиватися
процес, відома тільки передбачувана скінченна
множина (j = 1, 2, …, l) можливих сполучень
характеристик системи, що відповідає кожному зі
станів.
14

15. Реалізація моделей динамічного програмування

Для останнього k-го кроку точно відомо, до якого
результату він має привести – перевести систему з
j
S
одного з можливих її станів k 1 у єдино необхідний
Sk. Тому на останньому кроці керування залежить
тільки від стану системи після реалізації
передостаннього k–1 кроку, що дозволяє знайти
варіант, який забезпечує максимальний ефект
керування на останньому кроці, у якому б зі станів
S kj 1 не знаходилася система перед останнім кроком.
15

16. Реалізація моделей динамічного програмування

Розв’язання задачі динамічного програмування
починається з умовного планування останнього
кроку, тобто визначення множини можливих
керувань, кожне з яких переводить систему зі стану
S kj 1
j
S
у стан Sk. Оскільки стан k 1 системи перед
останнім кроком невідомий, то для кожного з
j
u
можливих станів знаходять відповідне керування i ,
яке називають умовно оптимальним. Після
S kj 1
визначення стану
системи перед останнім
кроком
з
умовно
оптимальних
керувань
вибирається одне безумовно оптимальне.
16

17. Задачі динамічного програмування

Методом динамічного програмування можуть
бути розв’язані такі задачі:
планування виробничої програми за періодами
року за мінімальних витрат на виробництво і
утримування запасів;
оптимальний розподіл коштів і ресурсів на
розширення виробництва за умови максимального
приросту випуску продукції;
оптимальне планування заміни застарілого
устаткування
новим
за
умови
одержання
максимального прибутку;
17

18. Задачі динамічного програмування

календарне планування ремонту або заміни
застарілого
устаткування
при
мінімумі
експлуатаційних витрат;
оптимальне резервування складних технічних
систем за мінімальних витрат на резервування, якщо
забезпечено надійність системи;
оптимальне
проектування
системи
стимулювання транспортних екіпажів за мінімумом
витрат енергії на зменшення шкідливих коливань за
умови забезпечення необхідних значень динамічних
показників у робочому діапазоні швидкостей руху.
18

19. Труднощі у динамічному програмуванні

Незважаючи
на достатню простоту
ідей
динамічного програмування, практична реалізація
математичних моделей стикається зі значними
труднощами.
По-перше, не існує єдиного методу й алгоритму
реалізації
різноманітних
моделей.
Способи
розв’язання задач з різним змістом різні, і практично
завжди нові змістовні постановки задач вимагають
розробки нових методів.
По-друге, саме розв’язання задач, як правило,
досить громіздке. Обсяг і трудомісткість роботи
різко зростають зі збільшенням кількості кроків і
можливих станів системи на кожному з них.
19

20. Труднощі у динамічному програмуванні

Відсутність єдиного способу реалізації моделей
призводить до того, що немає стандартних програм
розв’язування задач динамічного програмування на
комп’ютері. У свою чергу, це є стимулом для
розробки прикладного програмного забезпечення
розв’язання якої-небудь практичної задачі методом
динамічного програмування.
20

21. Задача заміни

Задача заміни — це прогнозування витрат,
пов’язаних з відновленням устаткування, і
виробленням найбільш економічної стратегії
проведення цієї роботи. В дослідженні операцій
виробляється ряд методів, котрі дозволяють
вирішувати задачі заміни двох типів:
коли продуктивність устаткування падає в
процесі експлуатації (внаслідок зносу) і воно
застаріває морально в результаті появи нових, більш
досконалих машин;
коли устаткування не застаріває, але в якийсь
момент
виходить
з
ладу
(наприклад,
електролампочки).
21

22. Задача заміни

У першому випадку порівнюються затрати та
придбання
нового
устаткування
з
витратами
експлуатації діючого і знаходиться оптимальний момент
заміни. Для вирішення деяких з цих задач
використовуються методи ДП.
У другому випадку визначають, які саме одиниці
потрібно заміняти та як часто проводити заміну, щоб
мінімізувати загальні затрати, пов’язані як з покупкою
нового устаткування, так і зі збитком, котрий наносить
несправне устаткування до його заміни. В цих задачах
широко використовуються фізико-статистичні методи
оскільки вихід із ладу устаткування завжди має
нерегулярний, вірогідний характер.
22

23. Задача про заміну устаткування

Відомо, що устаткування з часом зношується,
старіє фізично і „морально”. Як правило, в процесі
експлуатації його продуктивність падає і зростають
експлуатаційні видатки на поточний ремонт. З
часом виникає потреба заміни устаткування, так як
його подальша експлуатація виходить дорожче, ніж
ремонт та заміна.
23

24. Задача про заміну устаткування

В процесі роботи устаткування щорічно дає
прибуток, потребує експлуатаційних затрат і має
деяку
залишкову
вартість.
Перераховані
характеристики залежать від його віку.
На кожному році устаткування можна зберегти чи
продати за залишковою ціною, купити нове. У
випадку збереження устаткування зростають його
експлуатаційні
видатки
і
знижується
продуктивність. При заміні потрібні значні
додаткові капітальні вкладення.
24

25. Задача про заміну устаткування

Задача полягає у визначенні оптимальної
стратегії замін в плановому періоді в тому, щоб
сумарний прибуток за плановий період був
максимальним. Критерієм оптимальності, як
правило, є прибуток від експлуатації устаткування
(задача максимізації), або сумарні затрати на
експлуатацію в перебігу планованого періоду
(задача мінімізації).
При побудові моделі задачі прийнято вважати, що
рішення про заміну виноситься на початок кожного
проміжку експлуатації (наприклад, на початок року)
і
що
в
принципі
устаткування
можна
використовувати необмежено довго.
25

26. Задача про заміну устаткування

Основна
характеристика
устаткування
—
параметри стану — його вік t.
При складанні динамічної моделі заміни процес
заміни розглядають як n- кроковий, розвиваючи весь
період експлуатації на n кроків. Можливе
управління на кожному кроці характеризується
кількісними ознаками, наприклад: xc (зберегти
устаткування), х3 (замінити) та хр (зробити ремонт).
26

27. Задача про заміну устаткування

У статкування експлуатується протягом 4 років,
після цього продається.
На початку кожного року можна прийняти
рішення зберегти устаткування або замінити його
на нове. Вартість нового устаткування р0=2000 грн.
Після t років експлуатації (1 t 4) устаткування
можна продати за q(t)=p02-t грн. (ліквідна вартість).
Витрати на утримання протягом року залежать від
віку t устаткування і дорівнює r(t)=400(t+1).
Визначити оптимальну стратегію експлуатації
устаткування, щоб сумарні затрати з урахуванням
початкової покупки і завершальної продажі були
мінімальними.
27

28. Задача про заміну устаткування

Спосіб
розподілу
управління
на
кроки
природний, по роках, n=4. Параметр стану — вік
машини — s k 1 t , s 0 0 – машина нова на початку
першого року експлуатації. У правління на кожному
кроці залежить від двох змінних X С і X 3.
Рівняння станів залежать від управління:
t 1, якщо X k X C ,
sk
1, якщо X k X 3 , k 1, 2, 3.
(1)
28

29. Задача про заміну устаткування

Справді, якщо до k-му кроці sk-1=t, то при
збереженні машини (Х к=Х C) через рік вік машини
збільшиться на 1. Якщо машина заміняється новою
(Х к=X 3), то це означає, що до початку k-го кроку її вік
t=0, а після року експлуатації t=1, тобто sk=1.
Показник ефективності k-го кроку:
400(t 1), якщо X k X C ,
fk X k , t
2400 2000 2 t , якщо X k X 3 , k 1, 2, 3.
(2)
29

30. Задача про заміну устаткування

При X С витрати тільки на експлуатацію машини
віку t, при X 3 машина продається (-2000 2-t),
купується нова (2000) і експлуатується протягом
першого року (400), загальні витрати дорівнюють
(-2000 2-t+2000+400).
*
Z
Нехай k t — умовні оптимальні витрати на
експлуатацію машини, починаючи з k-го кроку до
кінця, за умови, що до початку k-го кроку машина
має вік t років.
30

31. Задача про заміну устаткування

Запишемо для функцій Z k t рівняння Беллмана,
замінивши задачу максимізації на задачу мінімізації:
*
t 1
C
400
(
t
1
)
2000
2
,
якщо
X
X
,
4
*
Z4
2400 2000 2 t 2000 2 t 1 , якщо X 4 X 3 . (3)
Величина 2000 2-(t+1) — вартість машини віку t
років (за умовою машина після 4 років експлуатації
продається).
400(t 1) Z k* 1 t 1 , якщо X k X C ,
Z k*
2400 2000 2 t Z k* 1 1 , якщо X k X 3 , k 3, 2,1. (4)
*
З визначення функцій Z k t випливає
Z min Z 1* 0 .
31

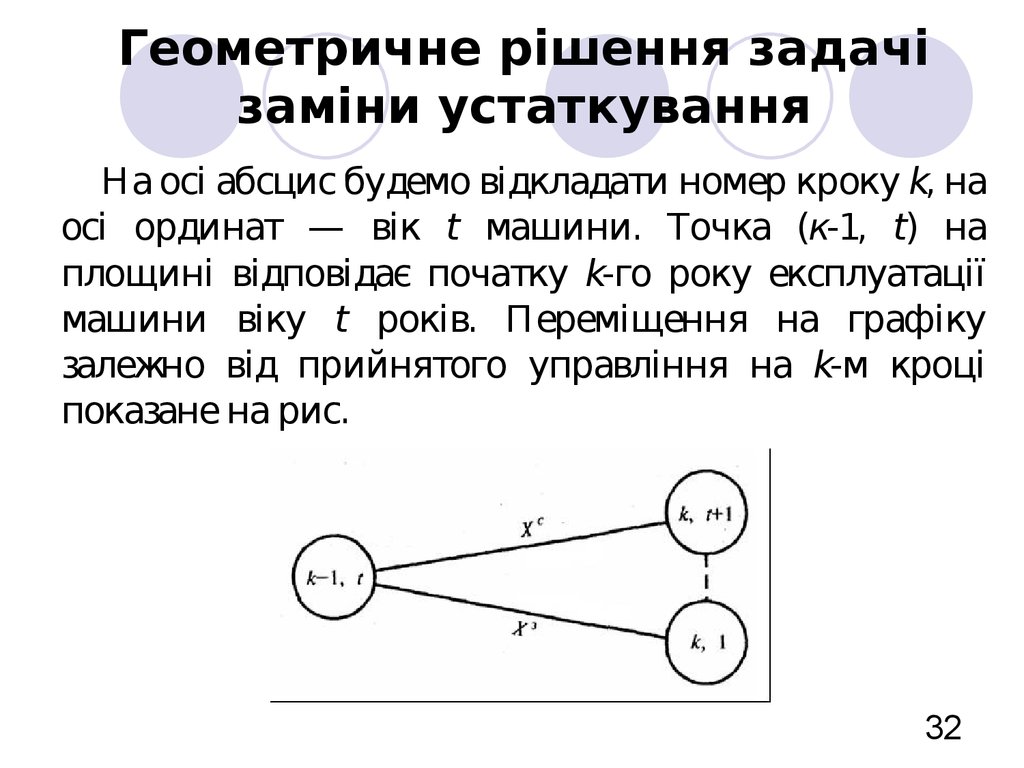
32. Геометричне рішення задачі заміни устаткування

На осі абсцис будемо відкладати номер кроку k, на
осі ординат — вік t машини. Точка (к-1, t) на
площині відповідає початку k-го року експлуатації
машини віку t років. Переміщення на графіку
залежно від прийнятого управління на k-м кроці
показане на рис.
32

33. Геометричне рішення задачі заміни устаткування

Стан початку експлуатації машини відповідає
*
точці s 0 (0; 0), кінець — точкам s (4; t). Будь-яка
*
s
траєкторія, що переводить точку s k 1;1 з 0 в s ,
складається з відрізків — кроків, що відповідають
рокам експлуатації. Треба вибрати таку траєкторію,
при якій витрати на експлуатацію машини
опиняться мінімальними.
33

34. Геометричне рішення задачі заміни устаткування

Над кожним відрізком, що з’єднує точки (k-1; t) і
(k; t+1), запишемо відповідному управлінню X С
витрати: 400(t+1), а над відрізком, що з’єднує точки
(k-1; t) і (k; t), запишемо витрати, що відповідають
управлінню X 3, тобто 2400-2000 2-t. У такий спосіб ми
розмітимо всі відрізки, що з’єднують точки на
графіку, які відповідають переходам з будь-якого
стану s k 1 в стан s k .
34

35. Геометричне рішення задачі заміни устаткування

Наприклад, над відрізками, що з’єднують точки
(k; 2) і (k+1; 3), стоїть число 1200, яке відповідає
витратам на експлуатацію протягом кожного року
машини віком t=2 років, а над відрізками, що
з’єднують (k; 2) і (k+1; 1), стоїть число 1900 — це сума
витрат на покупку машини й експлуатацію нової
машини протягом року без «витрат» (виручки) за
продану машину віку t років. Варто врахувати, що
0 t k.
35

36. Геометричне рішення задачі заміни устаткування

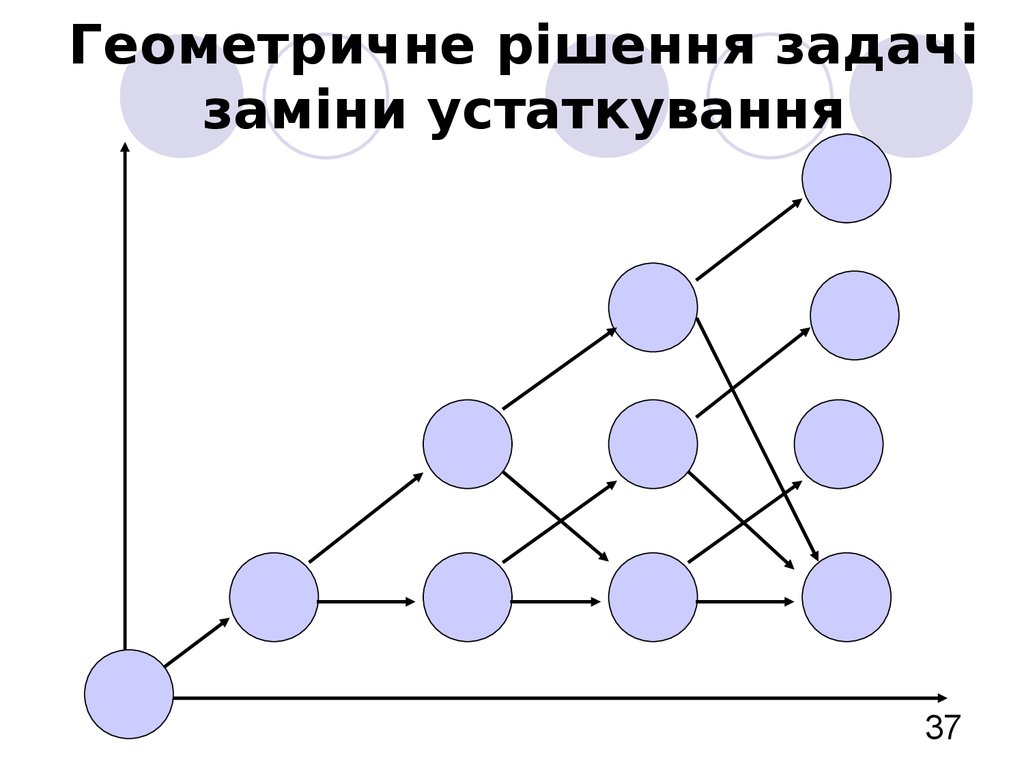
36

37. Геометричне рішення задачі заміни устаткування

37

38. Геометричне рішення задачі заміни устаткування

ІV крок. Початкові стани — точки (3; t), кінцеві
(4; t). У станах (4; t) машина продається, умовний
оптимальний дохід від продажу дорівнює 2000 2-t,
але оскільки цільова функція пов’язана з витратами,
то в кружках крапок (4; t) поставимо величину
доходу зі знаком мінус. Аналізуємо, як можна
потрапити з кожного початкового стану в кінцевий
на ІV кроці.
38

39. Геометричне рішення задачі заміни устаткування

Стан (3; 1). З нього можна потрапити в стан (4; 2),
затративши на експлуатацію машини 800 і
виручивши потім від продажу 500, тобто сумарні
витрати дорівнюють 300, і в стан (4; 1) з витратами
1400-1000=400. Виходить, якщо до останнього кроку
система перебувала в точці (3; 1), то варто йти в
точку (4;2) (укажемо цей напрямок подвійною
стрілкою), а неминучі мінімальні витрати, що
відповідають цьому переходу, рівні 300 (помістимо
цю величину Z 4* 1 300 в кружечку точки (3; 1).
39

40. Геометричне рішення задачі заміни устаткування

Стан (3; 2). З нього можна потрапити в точку (4; 3)
з витратами 1200-250=950 і в точку (4; 1) з витратами
1900-1000=900.
Вибираємо
друге управління,
*
відзначаємо його подвійною стрілкою, а Z 4 2 900
проставляємо в кружку точки (3; 2).
Міркуючи в такий спосіб для кожної точки
передостаннього кроку, ми знайдемо для будь-якого
результату IІІ кроку оптимальне управління на ІV
кроці, відзначимо його на рис. подвійною стрілкою.
Далі плануємо ІІІ крок, аналізуючи кожний стан, у
якому може виявитися система наприкінці II кроку з
урахуванням оптимального продовження до кінця
процесу, тобто вирішуємо для всіх 0 t 3 при k =
3.
40

41. Геометричне рішення задачі заміни устаткування

Наприклад, якщо початок ІІІ кроку відповідає
стану (2; 1), то при управлінні X С система
переходить у точку (3; 2), витрати на цьому кроці
800, а сумарні витрати за два останніх кроки
дорівнюють 900+800=1700. Так як при управлінні X 3
витрати за два кроки дорівнюють 300+1400=1700, що
співпадає ці станом при управлінні X С, то мінімальні
витрати дорівнюють 1700. Позначаємо подвійною
стрілкою альтернативні варіанти поведінки системи,
що веде зі стану (2; 1), у стан (3;2) або (3; 1). Так
розглядаємо для кожного стану (2; t).
41

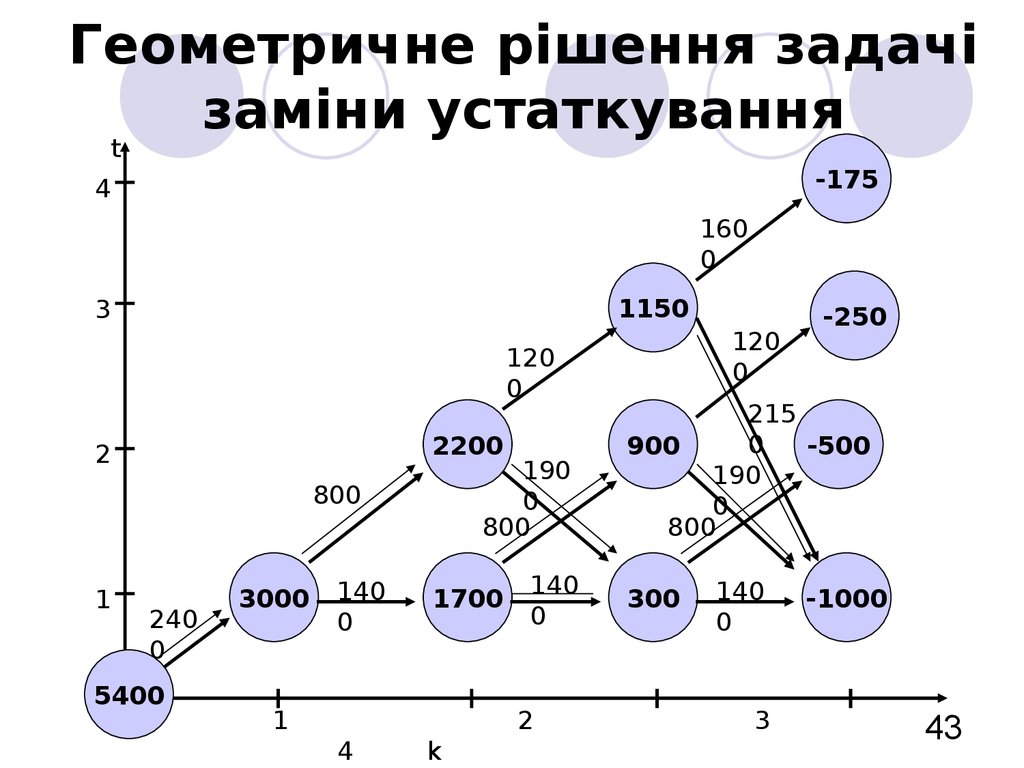
42. Геометричне рішення задачі заміни устаткування

Продовжуючи
умовну оптимізацію II і I кроків, ми
одержимо наступну ситуацію: з кожної точки
(стану) виходить стрілка (або дві подвійні стрілки,
якщо є альтернативні стани системи), що вказує,
куди варто переміщатися в даному кроці, якщо
система опинилась в цій точці, а в кружках записані
мінімальні витрати на перехід із цієї точки в
кінцевий стан. На кожному кроці графічно
вирішувалися рівняння (1).
Після проведення умовної оптимізації одержимо в
точці (0; 0) мінімальні витрати на експлуатацію
машини протягом 4 років з наступним продажем:
Z min =5400.
42

43. Геометричне рішення задачі заміни устаткування

t
-175
4
160
0
1150
3
120
0
2200
2
190
0
800
800
1
240
0
5400
3000
140
0
1700
1
140
0
2
4
k
120
0
-250
215
0
900
-500
190
0
800
300
140
0
3
-1000
43

44. Геометричне рішення задачі заміни устаткування

Далі
будуємо
оптимальну
траєкторію,
*
переміщаючись із точки s0 (0; 0) по подвійних
стрілках в s . Одержуємо набір точок:
{(0; 0), (1; 1), (2; 2), (3; 1), (4; 2)},
який відповідає оптимальному управлінню
X*=(X С, X С, X 3, X С).
Оптимальний режим експлуатації полягає в тому,
щоб замінити машину новою на початку 3-го року.
Таким чином, розмічений графік (мережа)
дозволяє наочно інтерпретувати розрахункову
схему й вирішити задачу методом ДП.
44

45. Тема 12: Задачі масового обслугову-вання

1. Сутність задач масового обслуговування
2.
Основні Планвизначення,
що
використовуються у системах масового
обслуговування
3.
Приклади
систем
масового
обслуговування
4.
Структура
систем
масового
обслуговування
5. Характеристики основних елементів СМО
6.
Класифікація
систем
масового
обслуговування
7. Моделі систем масового обслуговування
45
8. Порівняльна схема моделей систем

46. Сутність задач масового обслуговування

У повсякденному житті і у виробничій діяльності
широко розповсюджені системи, призначені для
багаторазового розв'язання однотипних задач.
Процеси, які при цьому виникають, отримали назву
процесів обслуговування, а системи — систем
масового обслуговування (СМО).
Система масового обслуговування (СМО) —
система, яка виконує обслуговування вимог, що
надходять до неї.
46

47. Основні визначення систем масового обслуговування

Системи масового обслуговування — це такі
системи, до яких у випадкові моменти часу
поступають замовлення на обслуговування, при
цьому замовлення, що надійшли, обслуговуються за
допомогою наявних у розпорядженні системи
каналів обслуговування.
47

48. Приклади систем масового обслуговування

пости ремонту автомобілів;
персональні комп'ютери, що обслуговують
замовлення;
станції технічного обслуговування автомобілів;
аудиторські фірми;
відділи податкових інспекцій, що займаються
прийманням і перевіркою поточної звітності підпр.;
перукарні;
світлофори;
підприємства харчування;
телефонні станції тощо.
48

49. Основні визначення систем масового обслуговування

Вимога (заявка) — запит на обслуговування.
Вхідний потік вимог — сукупність вимог, що
надходять у СМО.
Час обслуговування — період часу, протягом
якого обслуговується вимогу.
Математична модель СМО — це сукупність
математичних виразів, що описують вхідний потік
вимог, процес обслуговування та їх взаємозв'язок.
49

50. Основні визначення систем масового обслуговування

Теорія масового обслуговування (теорія черг) —
розділ теорії ймовірностей, метою досліджень якого
є
раціональний
вибір
структури
системи
обслуговування та процесу обслуговування на
основі вивчення потоків вимог на обслуговування,
що надходять у систему і виходять з неї, тривалості
очікування і довжини черг. У теорії масового
обслуговування використовуються методи теорії
ймовірностей та математичної статистики.
50

51. Історія виникнення задач масового обслуговування

Перші
задачі
ТМО
(теорії
масового
обслуговування) були розглянуті співробітником
Копенгагенської телефонної компанії Агнером
Ерлангом період між 1908 і 1922 роками. Стояло
завдання впорядкувати роботу телефонної станції і
заздалегідь розрахувати якість обслуговування
споживачів залежно від числа використовуваних
пристроїв.
51

52. Основні визначення систем масового обслуговування

В задачах масового обслуговування часто
необхідно визначити, яка кількість пристроїв
масового
обслуговування
необхідна,
щоб
мінімізувати сумарні втрати, що очікуються від
несвоєчасного
обслуговування
та
простою
обладнання.
52

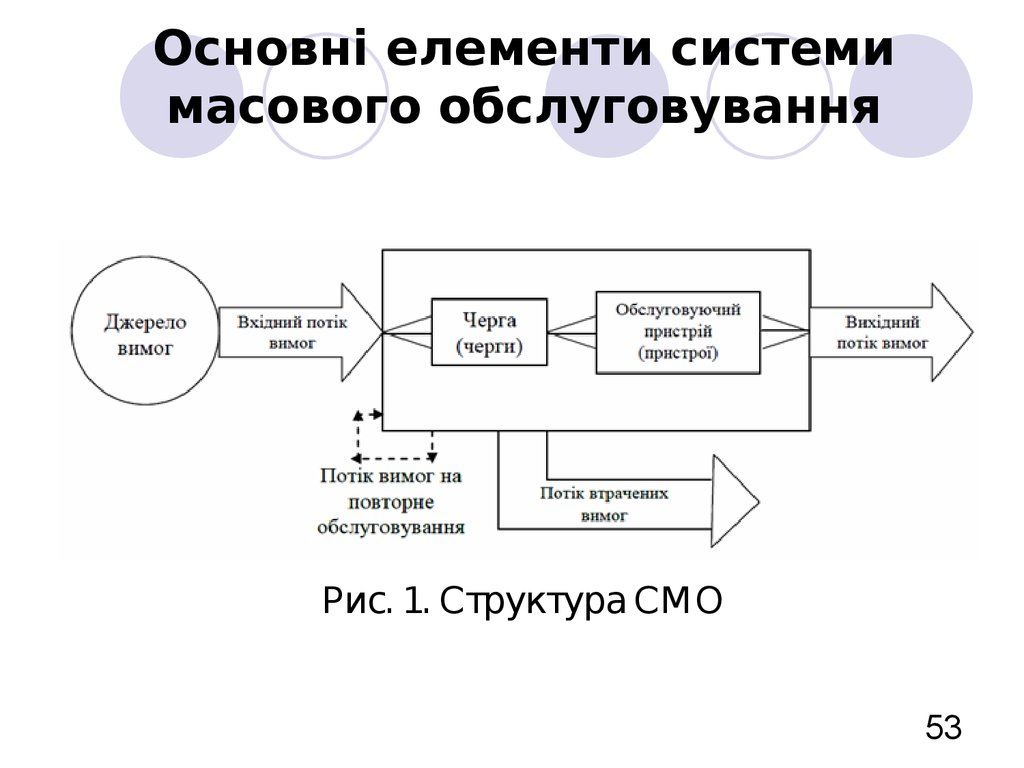
53. Основні елементи системи масового обслуговування

Рис. 1. Структура СМО
53

54. Характеристики основних елементів системи масового обслуговування

До основних елементів моделі
масового
обслуговування відносять клієнта (замовлення на
обслуговування) і сервіс (обслуговуючий пристрій,
прилад, засіб обслуговування тощо).
Клієнти надходять до системи обслуговування з
джерела клієнтів (джерела вимог).
Джерело вимог — це генератор клієнтів.
Основною характеристикою джерела вимог є
його потужність, яка може бути скінчена і
нескінчена.
54

55. Характеристики основних елементів системи масового обслуговування

Вхідній потік вимог визначає послідовність
моментів надходження вимог на обслуговування і
зазначає кількість таких вимог у кожному черговому
надходженні. Для описання вхідного потоку
потрібно задати закон розподілу ймовірностей, що
управляє послідовністю моментів надходження
вимог на обслуговування і зазначити кількість таких
вимог у кожному черговому надходженні.
55

56. Характеристики основних елементів системи масового обслуговування

Характеристикою потоку вимог є λ.
λ — інтенсивність надходження замовлень в
систему, тобто середня кількість замовлень, що
надходять в систему за одиницю часу.
Вихідний
потік
вимог
характеризується
інтенсивністю μ.
μ — інтенсивність обслуговування, тобто число
вимог, обслужених за одиницю часу, протягом якого
прилад зайнятий обслуговуванням. Існує залежність
між часом обслуговування та інтенсивністю
обслуговування.
56

57. Характеристики основних елементів системи масового обслуговування

Черга — ряд замовлень, що очікують на
обслуговування. Розрізняють дві її характеристики
— довжину (місткість) і дисципліну черги.
Довжина черги може бути скінчена і нескінчена.
Дисципліна черги визначає принцип, відповідно до
якого обслуговуються замовлення в системі.
57

58. Характеристики основних елементів системи масового обслуговування

Приклади дисципліни черги:
FCFS /
FIFO (що прийшов першим
обслуговується першим);
LCFS /
LIFO (що прийшов останнім
обслуговується першим);
RANDOM (випадковий вибір);
добір замовлень за критерієм пріоритетності;
обмеження часу очікування моменту настання
обслуговування («припустима довжина черги»).
58

59. Характеристики основних елементів системи масового обслуговування

При дослідженні
СМО можуть розв'язуватися:
1) задачі аналізу СМО – визначення характеристик
якості обслуговування залежно від параметрів і
властивостей вхідного потоку вимог, параметрів і
структури і дисципліни СМО;
2) задачі параметричного синтезу – визначення
параметрів системи обслуговування при заданій
структурі залежно від параметрів і властивостей потоку
вимог, дисципліни і якостей обслуговування;
3) задачі синтезу структури системи з оптимізацією її
параметрів таким чином, щоб при заданих потоках,
дисципліні і якості обслуговування вартість СМО була
мінімальною або були мінімальними втрати замовлень
при заданих потоках, дисципліні і вартості системи.
59

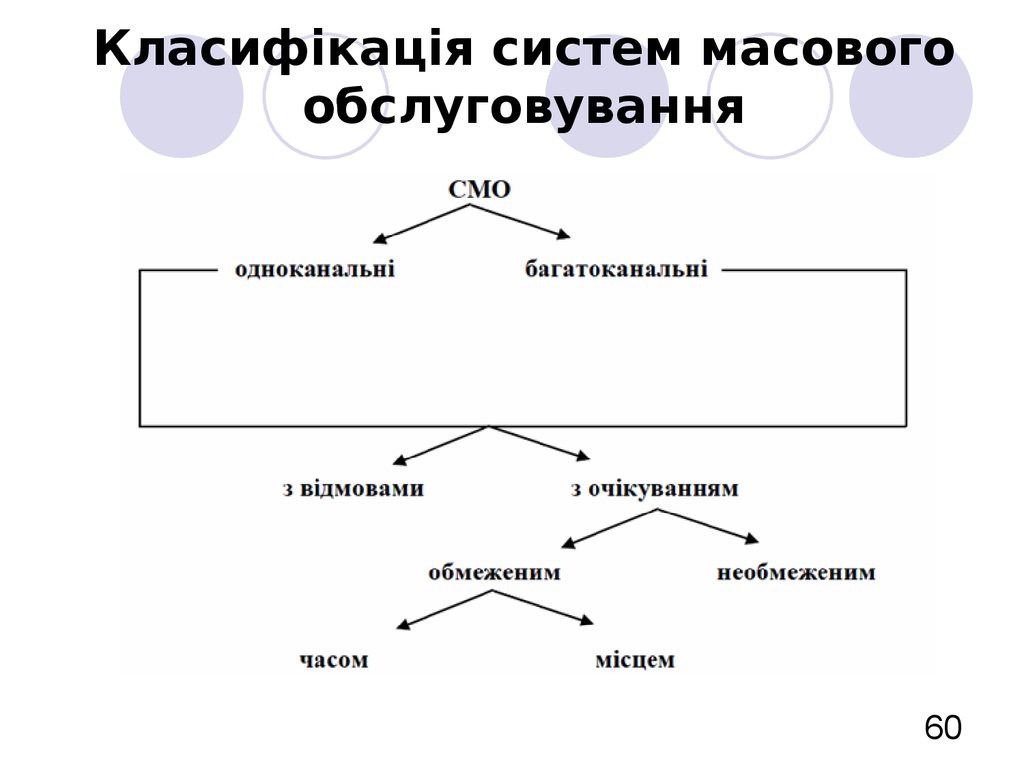
60. Класифікація систем масового обслуговування

60

61. Класифікація систем масового обслуговування

Класифікація СМО за складом:
одноканальні
(з
одним
обслуговуючим
пристроєм);
багатоканальні (з декількома паралельними
обслуговуючими пристроями).
61

62. Класифікація систем масового обслуговування

За
складом
обслуговуючих
пристроїв
багатоканальні СМО поділяють на:
однофазні (якщо після проходження одного
обслуговуючого пристрою замовлення вважається
обслуженим);
багатофазні (замовлення повинно послідовно
пройти через декілька обслуговуючих пристроїв).
62

63. Класифікація систем масового обслуговування

Класифікація за часом перебування вимоги в
системі до початку обслуговування:
з відмовами (якщо замовлення, що надійшло до
системи, не може бути обслужене, воно покидає
систему);
з очікуванням (замовлення, що надійшло до
системи у момент, коли всі канали зайняті,
становиться в чергу і очікує на обслуговування).
Очікування
може
бути
обмеженим
і
необмеженим. Обмежуватись очікування може
часом очікування або довжиною черги.
63

64. Моделі систем масового обслуговування

Всі наступні моделі мають такі загальні
характеристики:
а) пуасоновський
розподіл
ймовірностей
надходження заявок;
б) стандартна поведінка клієнтів;
в) правило обслуговування FIFO (першим
прийшов — першим обслужений);
г) єдина фаза обслуговування.
64

65. Моделі систем масового обслуговування

I. Модель А — модель одноканальної системи
масового обслуговування М/ М/ 1 з пуасоновським
вхідним потоком заявок і експонентним часом
обслуговування.
Найбільше часто зустрічаються задачі масового
обслуговування з єдиним каналом. У цьому випадку
клієнти формують одну чергу до єдиного пункту
обслуговування.
65

66. Моделі систем масового обслуговування

Припущення:
1. Заявки обслуговуються за принципом FIFO,
причому кожний клієнт очікує своєї черги до кінця
незалежно від довжини черги.
2. Появи заявок є незалежними подіями, однак
середнє число заявок, що надходять в одиницю часу,
незмінно.
3. Процес
надходження
заявок
описується
пуасоновським розподілом, причому заявки надходять із
необмеженої кількості.
4. Час обслуговування описується експонентним
розподілом ймовірностей.
5. Темп обслуговування вище темпу надходження
заявок.
66

67. Моделі систем масового обслуговування

Нехай — число заявок в одиницю часу;
— число клієнтів, що обслуговуються в
одиницю часу;
n — число заявок у системі.
67

68. Моделі систем масового обслуговування

Формули для опису системи М/М/1:
— середнє число клієнтів у системі;
— середній час обслуговування одного
клієнта в системі (час очікування плюс час
обслуговування);
— середнє число клієнтів у черзі;
— середній час очікування клієнта
в черзі;
68

69. Моделі систем масового обслуговування

— характеристика завантаженості системи
(частка часу, протягом якого система зайнята
обслуговуванням);
— ймовірність відсутності заявок у
системі;
— ймовірність того, що в системі
перебуває більш ніж k заявок.
69

70. Моделі систем масового обслуговування

II. Модель В —
багатоканальна система
обслуговування M/ M/ S. У багатоканальній системі
для обслуговування відкриті два канали або більше.
Передбачається, що клієнти очікують у загальній
черзі й звертаються в перший канал обслуговування,
що звільнився.
Приклад такої багатоканальної однофазової
системи можна побачити в багатьох банках: із
загальної
черги
клієнти
звертаються
для
обслуговування в перше віконце, що звільнилося.
70

71. Моделі систем масового обслуговування

Для багатоканальної системи з необмеженою
r
1
чергою повинна виконуватися умова n
, де r —
параметр завантаження системи (середнє число
зайнятих каналів), n — мінімальна кількість каналів,
при якому черга не буде рости нескінченно. У
противному випадку граничні ймовірності існувати
не можуть.
71

72. Моделі систем масового обслуговування

Формули для опису системи M/M/S:
—
ймовірність того, що система вільна;
— ймовірність того, що в системі
перебуває п заявок;
— ймовірність того, що заявка
виявиться в черзі;
72

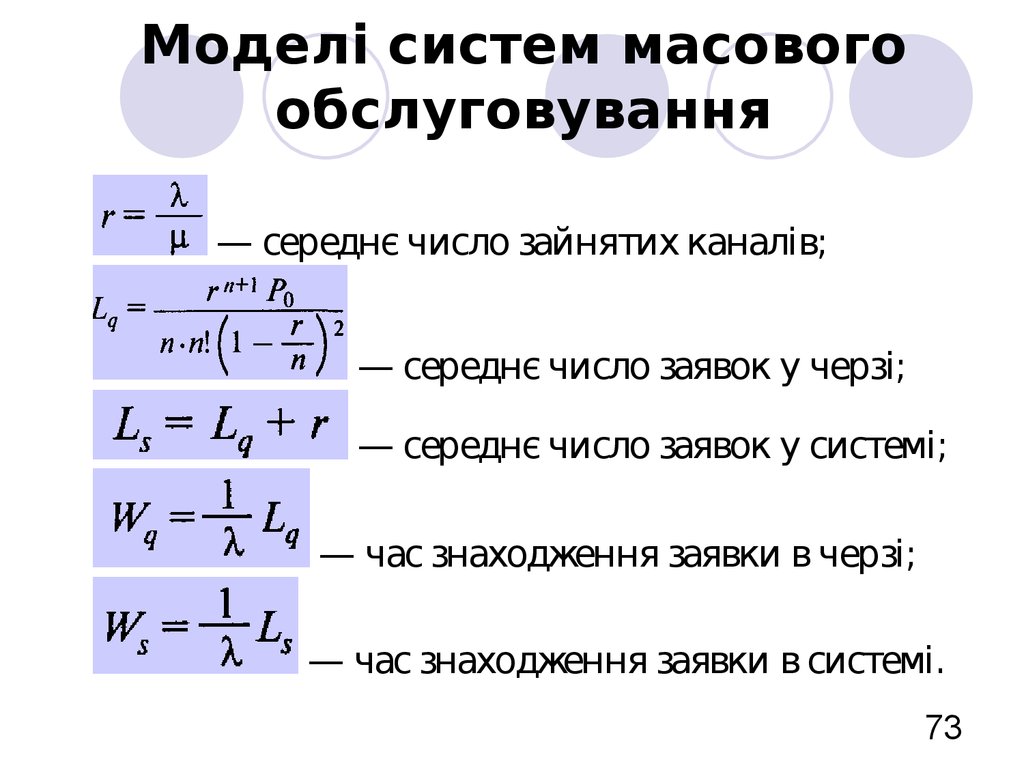
73. Моделі систем масового обслуговування

— середнє число зайнятих каналів;
— середнє число заявок у черзі;
— середнє число заявок у системі;
— час знаходження заявки в черзі;
— час знаходження заявки в системі.
73

74. Моделі систем масового обслуговування

III. Модель С — модель із постійним часом
обслуговування M/ D/ 1.
Деякі системи мають постійне, а не експонентно
розподілений час обслуговування. У таких системах
клієнти обслуговуються протягом фіксованого
періоду часу, як, наприклад, на автоматичній мийці
автомобілів. Для моделі С з постійним темпом
обслуговування значення величин Lq і Wq удвічі
менші, ніж відповідні значення в моделі А, що має
змінний темп обслуговування.
74

75. Моделі систем масового обслуговування

Формули, що описують модель M/D/1:
— середня довжина черги;
— середній час очікування в черзі;
— середнє число клієнтів у системі;
— середній час очікування в
системі.
75

76. Моделі систем масового обслуговування

IV. Модель D — модель із обмеженою популяцією.
Якщо число потенційних клієнтів системи
обслуговування обмежено, ми маємо справу зі
спеціальною моделлю. Таке завдання може
виникнути, наприклад, якщо мова йде про
обслуговування устаткування фабрики, що має
п’ять верстатів.
Особливість цієї моделі в порівнянні із трьома
розглянутими
раніше у
тому,
що
існує
взаємозалежність між довжиною черги й темпом
надходження заявок.
76

77. Моделі систем масового обслуговування

V. Модель Е — модель із обмеженою чергою.
Модель відрізняється від попередніх тим, що число
місць у черзі обмежено. У цьому випадку заявка, що
прибула в систему, коли всі канали й місця в черзі
зайняті, залишає систему не обслуженою, тобто
одержує відмову.
Як окремий випадок моделі з обмеженою чергою
можна розглядати модель із відмовами, якщо
кількість місць у черзі скоротити до нуля.
77

78. Порівняльна схема моделей систем масового обслуговування

78

79. Список літератури

Основна:
1. Зайченко Ю. П. Дослідження операцій :
підручник / Ю. П. Зайченко. – К. : ВІПОЛ, 2000.
2. Таха Х. Введение в исследование операций /
Х. Таха. – М. : Вильямс, 2001.
3. Ульянченко О. В. Дослідження операцій в
економіці / О. В. Ульянченко. – Х. : Гриф, 2003.
Додаткова:
1.
Вітлінський В. В.
Математичне
програмування
/
В. В. Вітлінський,
С. І. Наконечний, Т. О. Терещенко. – К., 2001.
2.
Кузнецов А. В.
Математическое
программирование / А. В. Кузнецов и др. – М.:
Высшая школа, 1994.
79