Similar presentations:
Построение сечений тетраэдра и параллелепипеда
1.
2.
Новые понятия в теме:•Секущая плоскость тетраэдра (параллелепипеда) –
любая плоскость, по обе стороны от которой имеются точки
данного тетраэдра (параллелепипеда)
В1
•Cечение многогранника –
многоугольник, сторонами которого
являются отрезки, по которым
пересекает грани многогранника
секущая плоскость
Назовите отрезки, по которым секущая
плоскость пересекает грани параллелепипеда:
верхнюю, нижнюю, правую, левую, переднюю,
заднюю
Назовите сечение параллелепипеда
С1
А1
Д1
В
С
А
Д
М
В
Назовите сечение тетраэдра
А
3.
При построении сечений важно знать:а) если две точки многогранника принадлежат
сечению, то прямая, проходящая через них,
принадлежит секущей плоскости
Теоретические основы:
По аксиоме: если две точки прямой лежат в
плоскости, то все точки прямой, лежат в этой
плоскости
4.
При построении сечений важно знать:б) если секущая плоскость пересекает две
противоположные параллельные грани
многогранника, то
линии пересечения параллельны
Теоретические основы:
По теореме: если две параллельные
плоскости пересекаются третьей
плоскостью, то линии их пересечения
параллельны
5.
При построении сечений важно знать:в) если секущая плоскость проходит через
прямую, параллельную грани многогранника и
пересекает её, то
линия пересечения плоскости и грани
параллельна данной прямой
Теоретические основы:
Если плоскость проходит через
прямую, параллельную другой
плоскости, и пересекает эту
плоскость, то линия пересечения
параллельна данной прямой
6.
При построении сечений важно знать:д) общая точка секущей плоскости и
плоскостей двух пересекающихся
граней лежит на
прямой, содержащей общее ребро граней
Теоретические основы:
Если прямая, лежащая в одной из
пересекающихся плоскостей,
пересекает другую плоскость, то она
пересекает и линию пересечения
плоскостей
а
С
Х
В
А
7.
При построении сечений важно знать:а) построение сечения сводится к построению линий
пересечения секущей плоскости с гранями
многогранника
б) сечение однозначно определяется тремя
точками многогранника
8.
Правила построения сечений1) если две точки многогранника принадлежат сечению,
то прямая, проходящая через них, принадлежит секущей
плоскости
Что делаем, если в плоскости какой-то грани
2) окажутся
если секущая
пересекает
две ?противоподве плоскость
точки секущей
плоскости
ложные параллельные грани многогранника, то линии
пересечения параллельны;
Что делаем,
в одной
из параллельных
граней двух
естьпере3) Общая
точкаесли
секущей
плоскости
и плоскостей
сторона
сечения,
а в на
другой
- точка
сечения? общее
секающихся
граней
лежит
прямой,
содержащей
ребро граней
Что делаем, если в одной из пересекающихся
граней есть две точки сечения, а в другой - еще
одна?
Х
С
В
А
9.
НК
М
М
С
К
М
3)
1)
Н
2) К
10.
ВТочка
Грань
На которой
L
М
оборвалось
сечение
в которой надо
нижняя
правая
построить
сечение
Прямая
Плоскость
Линия пересечения
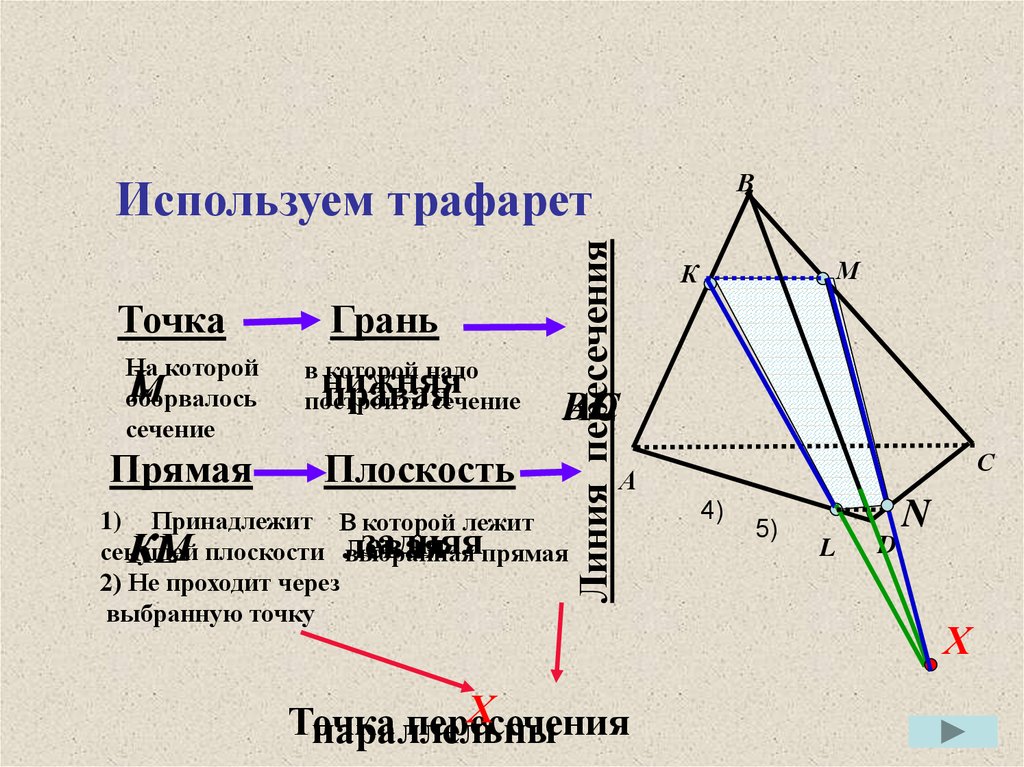
Используем трафарет
М
К
BD
АС
1) Принадлежит В которой лежит
задняяпрямая
секущей
КМ плоскости левая
выбранная
КL
2) Не проходит через
выбранную точку
С
А
Х
Точка
пересечения
параллельны
4)
5)
N
L
D
Х
11.
Ребро куба АВСДА1В1С1Д1 равно b. Секущая плоскостьпроходит через середины ребер АВ, АА1 и А1Д1.
Найдите площадь сечения.
Р
Д1
С1
А1
К
Сечение – правильный шестиугольник
Д
С
А
Х
Sсеч = 6*S ΔKOM
О
М
В
∆КОМ - равносторонний
КМ
Е
6)
АК 2 АМ 2
b 2
2
2
S КОМ
b 2
3 b2 3
* 4 8
2
S сеч 6 * S ком
а2 3
S
4
b2 3 3 3 2
6*
b
8
4
12.
Построим сечения сами!S
Н
Построить сечения тетраэдра SKLM
проходящее через ребро КS и
высоту SО.
К
М
K
M
O
N
L
К
М
13.
Построим сечения сами!S
Н
С
N
К
М
K
M
O
N
L
С
К
М
Х
14.
Среди равных умов приодинаковости прочих условий
превосходит тот, кто знает
геометрию.
Блез Паскаль














 mathematics
mathematics








