Similar presentations:
Многоугольники вокруг нас
1. Многоугольники вокруг нас
Составитель: Критинина О. М.учитель математики
МКОУ БООШ №5
2.
Паркетный пол во все временасчитался символом престижа
и хорошего вкуса.
Сама история
художественного паркета
очень древняя - она датируется
приблизительно 12 столетием..
Первый художественный
паркет выкладывался
достаточно примитивно, с
точки зрения современности из обычных деревянных
кусочков, подходящих по
цвету. Сегодня доступно
формирование сложных
орнаментов и мозаичных
сочетаний. Это достигается
благодаря лазерной и
механической резке высокой
точности.
3.
Астрономам сегодня известно,что на Красной планете
имеются крупные, в диаметре
от сотни до тысячи метров,
многоугольные образования.
Как и откуда они появились —
вот предмет настоящих дебатов
исследователей. Что касается
многоугольников — они
обнаружены, по большей части,
в северных равнинах Красной
планеты. На нашей планете
такие многоугольники хорошо
видны в Норвежском и
Северном морях, т.е. там, где
глубина больше пятисот
метров. Это дает основание
ученым предполагать, что
древний Марс был покрыт
такими же морями, в результате
чего и сформировался его
современный рельеф.
4.
В III веке до н.э. былпостроен маяк, чтобы
корабли могли благополучно
миновать рифы на пути в
александрийскую бухту. Это
был первый в мире маяк, и
простоял он 1500 лет
Александрийский маяк
состоял из трех мраморных
башен. Первая башня была
прямоугольной, в ней
находились комнаты, в
которых жили рабочие и
солдаты. Над этой башней
располагалась меньшая,
восьмиугольная башня со
спиральным пандусом,
ведущим в верхнюю башню.
Верхняя башня формой
напоминала цилиндр, в
котором горел огонь,
помогавший кораблям
благополучно достигнуть
бухты. Общая высота маяка
составляла 117 метров.
5. Пчёлы – удивительные творения природы. Свои геометрические способности они проявляют при построении сот.
Пчелиные соты представляютсобой прямоугольник,
покрытый правильными
шестиугольниками
6.
Танграмм – это известная всемумиру игра, созданная на основе
древних китайских головоломок.
По легенде, 4 тысячи лет назад у
одного мужчины выпала из рук
керамическая плитка и разбилась
на 7 частей. Взволнованный, он
посохом попытался её собрать.
Но из вновь составленных частей
каждый раз получал новые
интересные изображения. Это
занятие вскоре оказалось
настолько захватывающим,
головоломным, что
составленный квадрат из семи
геометрических фигур назвали
Доской Мудрости. Если разрезать
квадрат, как показано на рисунке
выше, то получится популярная
китайская головоломка
ТАНГРАМ. У нас она сейчас
распространена под названием
"Пифагор"
7. До сих пор многоугольники нередко называют в науке по-гречески с окончанием “гон”: полигон – многоугольник, пентагон –
пятиугольник(такой формы сверху здание Театра Российской Армии в Москве и Министерства
обороны США в Вашингтоне)
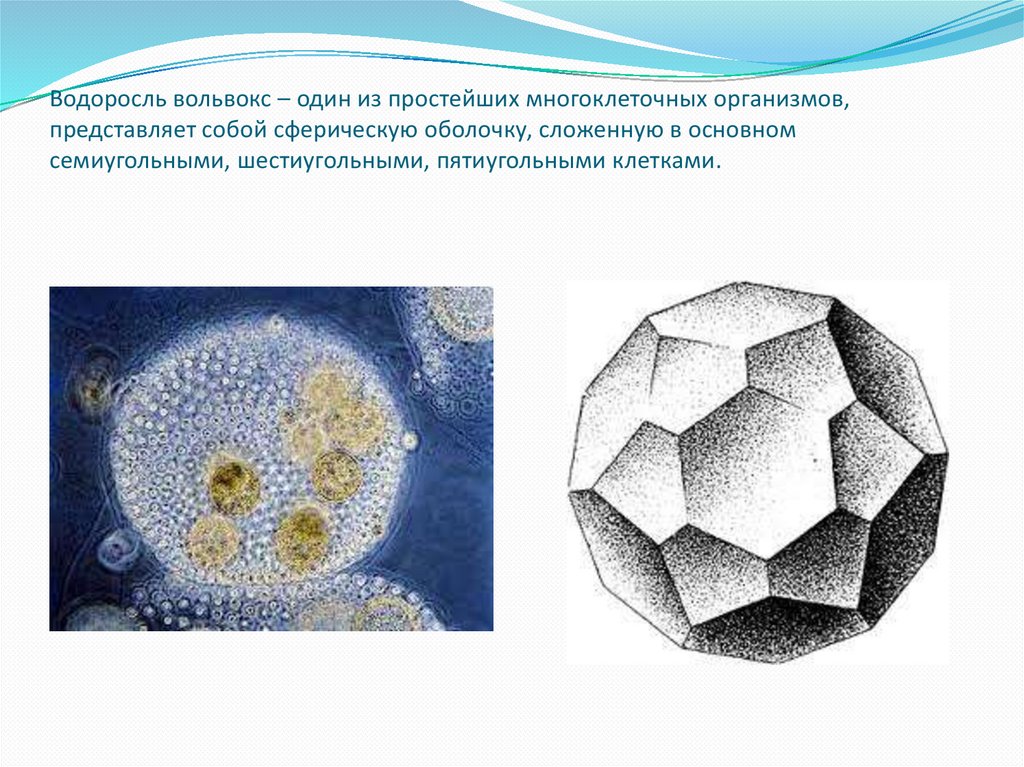
8. Водоросль вольвокс – один из простейших многоклеточных организмов, представляет собой сферическую оболочку, сложенную в
основномсемиугольными, шестиугольными, пятиугольными клетками.
9. Берму́дский треуго́льник — район в Атлантическом океане, в котором якобы происходят таинственные исчезновения морских и
Берму́дский треуго́льник — район в Атлантическом океане, в котором якобыпроисходят таинственные исчезновения морских и воздушных судов. Район
ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и
назад к Флориде через Багамы.
10.
«Математика владеет не только истинной , нои высшей красотой – красотой отточенной и
строгой, возвышенно чистой и стремящейся к
подлинному совершенству, которое
свойственно лишь величайшим образцам
искусства»
Бертран Рассел









 mathematics
mathematics








