Графики функций1. Готовимся к ОГЭ

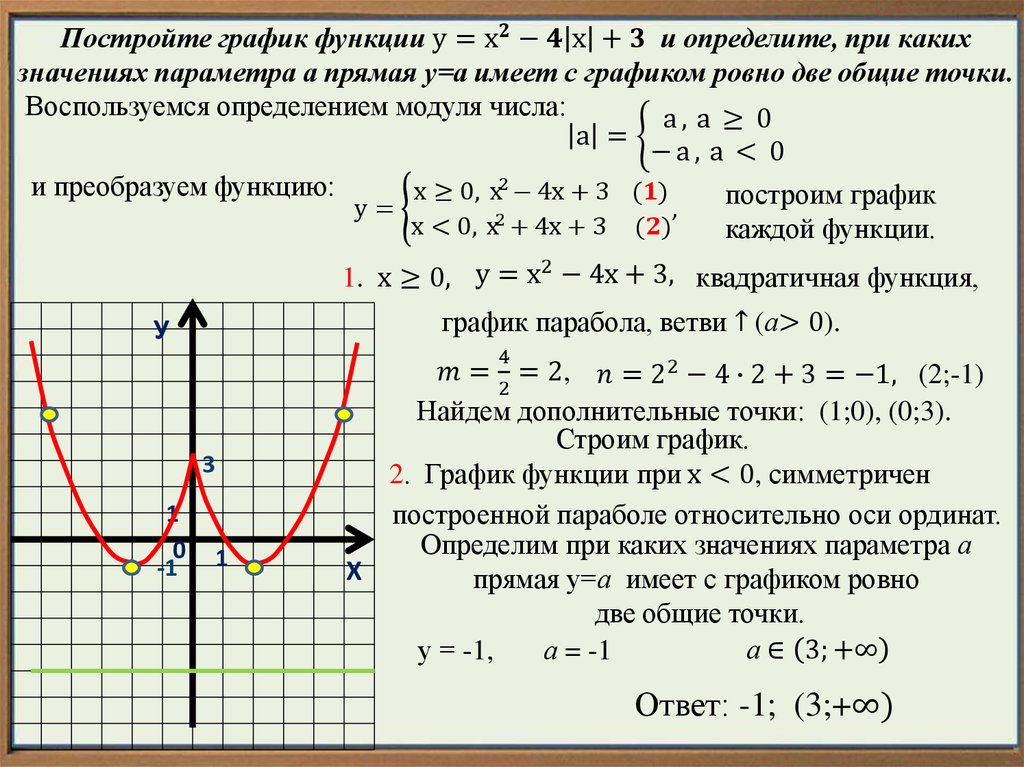
1. Готовимся к ОГЭ – 2018 Задание 23 Графики функций

2.

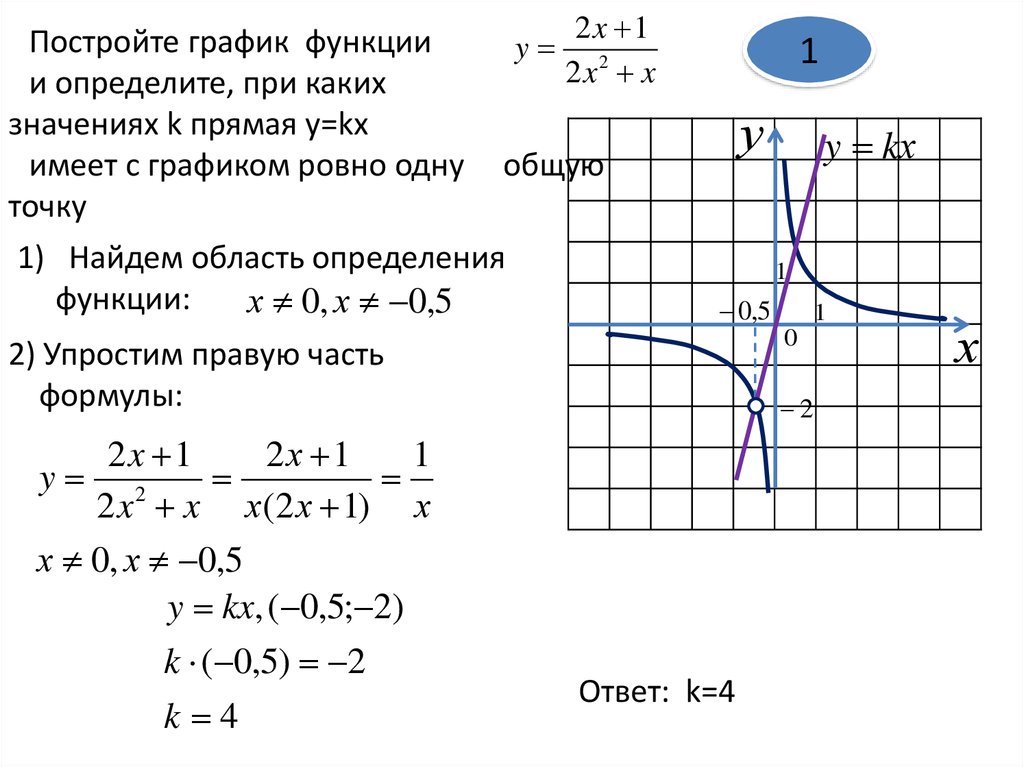
2x 1
Постройте график функции
y 2
2x x
и определите, при каких
значениях k прямая y=kx
имеет с графиком ровно одну общую
точку
1) Найдем область определения
функции:
х 0, х 0,5
1
у
1
0,5
2
2x 1
2х 1
1
y 2
2 x x х(2 х 1) х
х 0, х 0,5
y kx, ( 0,5; 2)
k 4
1
0
2) Упростим правую часть
формулы:
k ( 0,5) 2
y kх
Ответ: k=4
х

3.

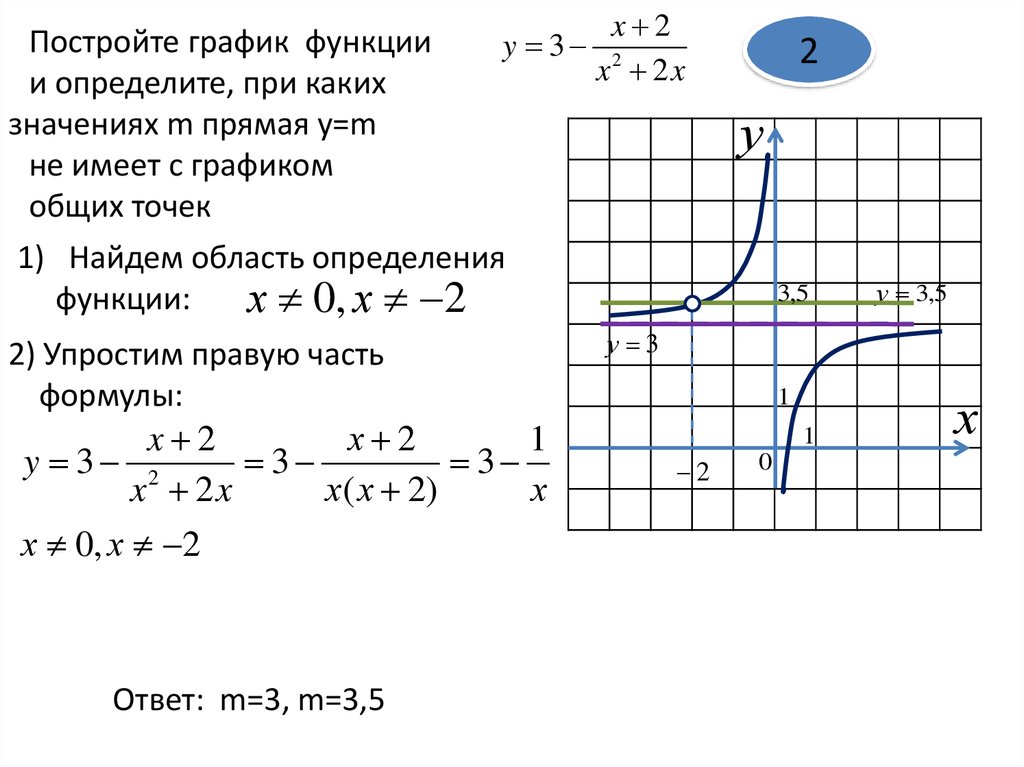
x 2
Постройте график функции
y 3 2
x 2x
и определите, при каких
значениях m прямая y=m
не имеет с графиком
общих точек
1) Найдем область определения
функции:
х 0, х 2
2) Упростим правую часть
формулы:
x 2
х 2
1
y 3 2
3
3
x 2x
х ( х 2)
х
х 0, х 2
Ответ: m=3, m=3,5
2
у
3,5
у 3,5
у 3
1
1
2
0
х

4.

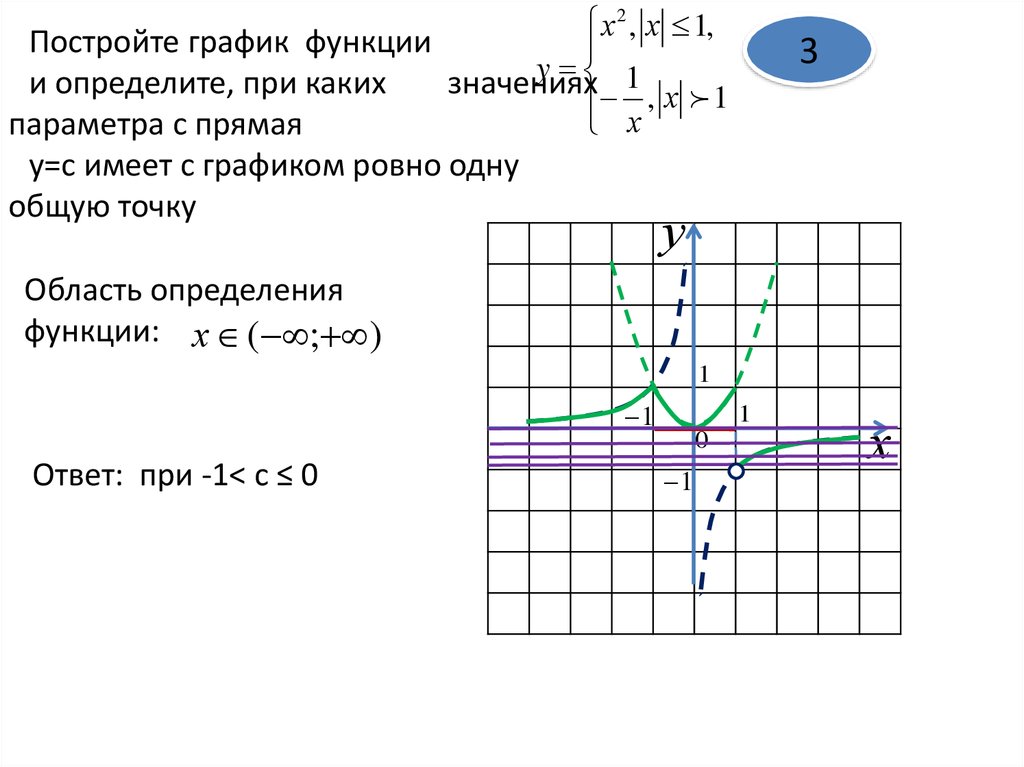
х 2 , х 1,
Постройте график функции
y 1
и определите, при каких
значениях
, х 1
х
параметра с прямая
y=с имеет с графиком ровно одну
общую точку
3
у
Область определения
функции: х ( ; )
1
1
1
0
Ответ: при -1< c ≤ 0
1
х

5.

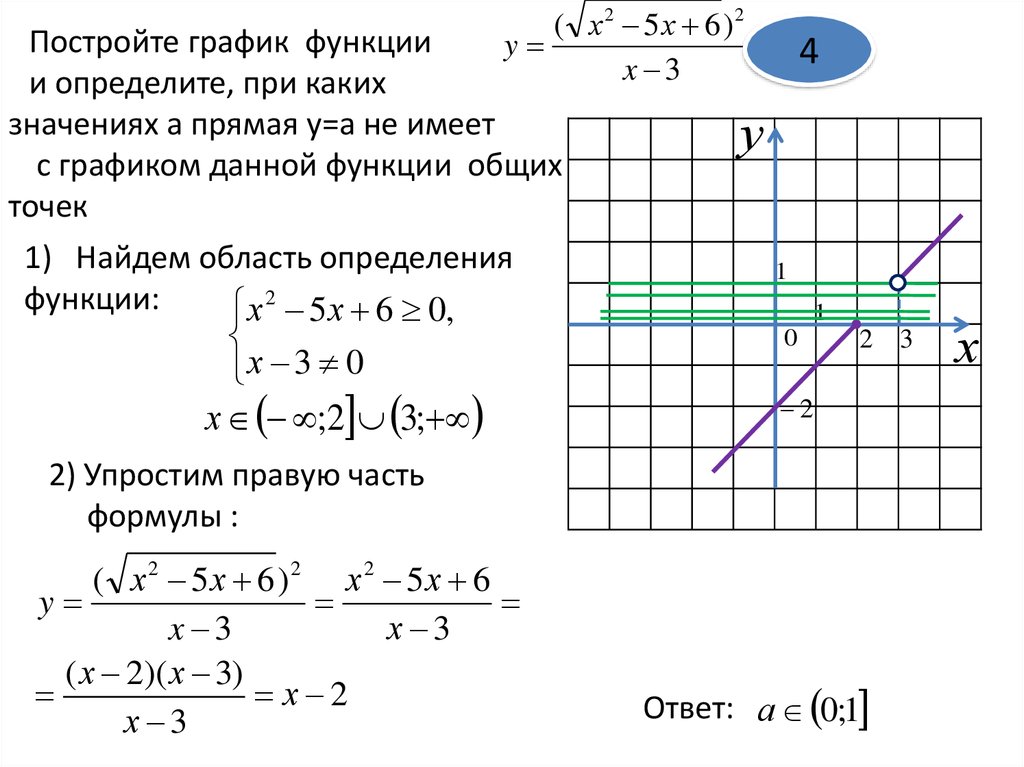
( х 2 5 х 6 )2
y
x 3
Постройте график функции
и определите, при каких
значениях а прямая y=а не имеет
с графиком данной функции общих
точек
1) Найдем область определения
функции:
х 2 5 х 6 0,
х 3 0
х ;2 3;
4
у
1
1
0
2
2
2) Упростим правую часть
формулы :
( х 2 5 х 6 )2 х 2 5 х 6
y
x 3
х 3
( х 2)( х 3)
х 2
х 3
Ответ: а 0;1
3
х

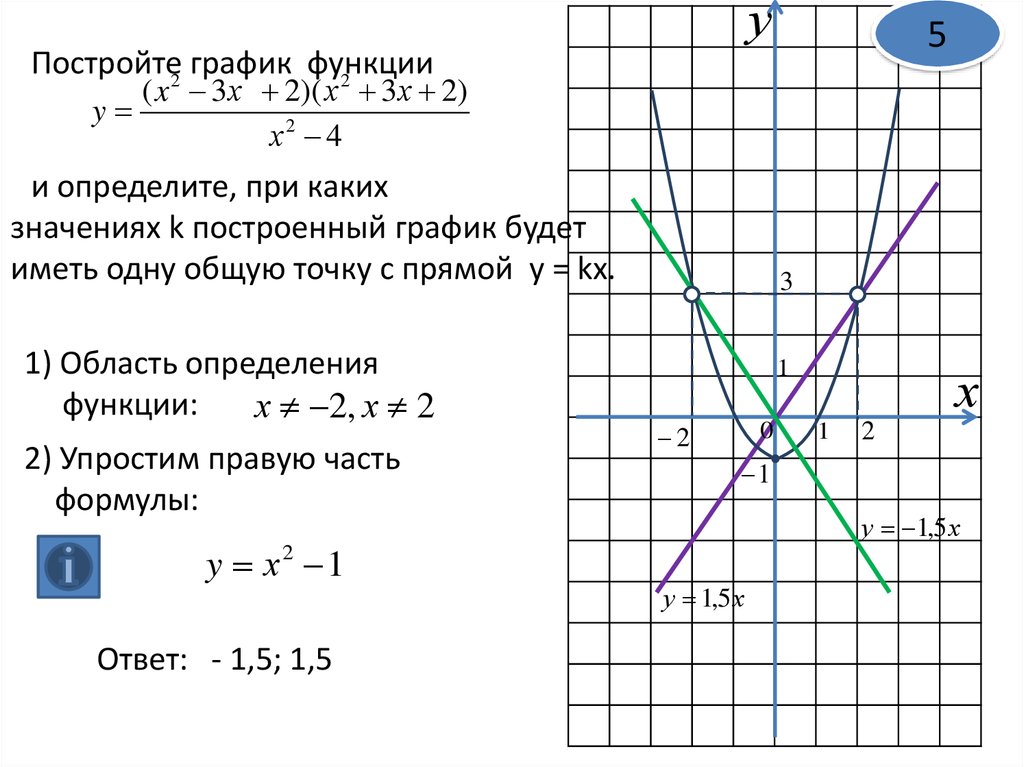
6.

у
5
Постройте2 график функции
2
( x 3 х 2)( х 3 х 2)
y
х2 4
и определите, при каких
значениях k построенный график будет
иметь одну общую точку с прямой у = kx.
1) Область определения
функции:
х 2, х 2
2) Упростим правую часть
формулы:
y х2 1
Ответ: - 1,5; 1,5
3
1
2
0
х
1
2
1
у 1,5 х
у 1,5 х

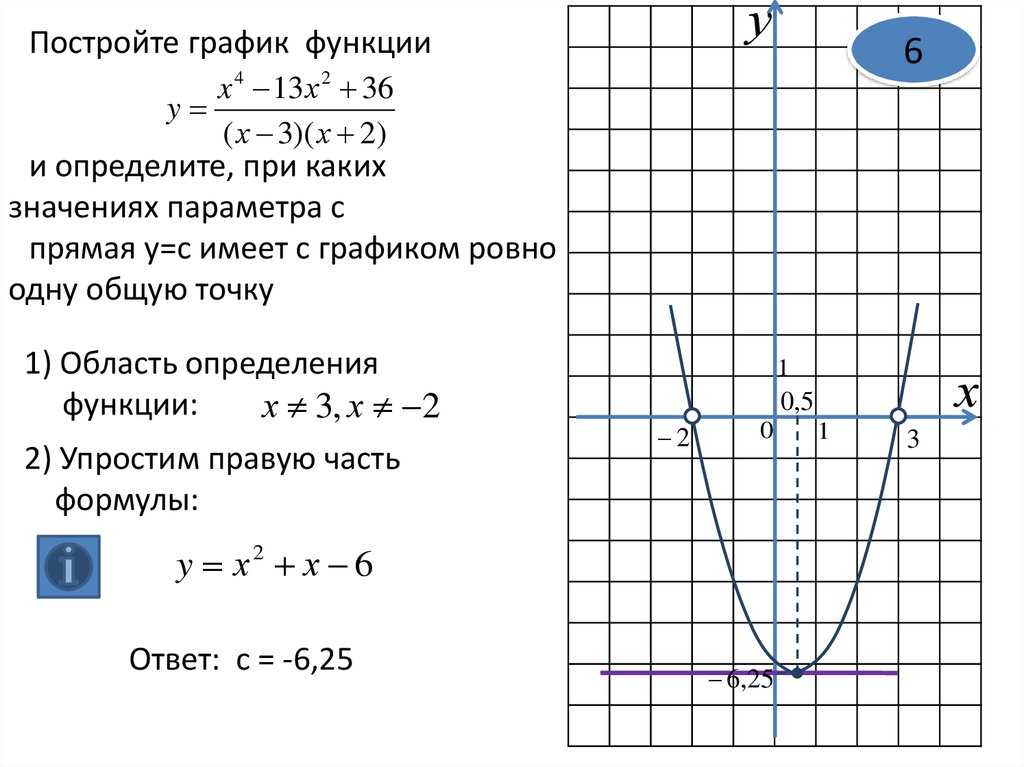
7.

у
Постройте график функции
6
x 4 13 х 2 36
y
( х 3)( х 2)
и определите, при каких
значениях параметра с
прямая y=с имеет с графиком ровно
одну общую точку
1) Область определения
функции:
х 3, х 2
2) Упростим правую часть
формулы:
1
2
0
y х2 х 6
Ответ: с = -6,25
х
0,5
6,25
1
3

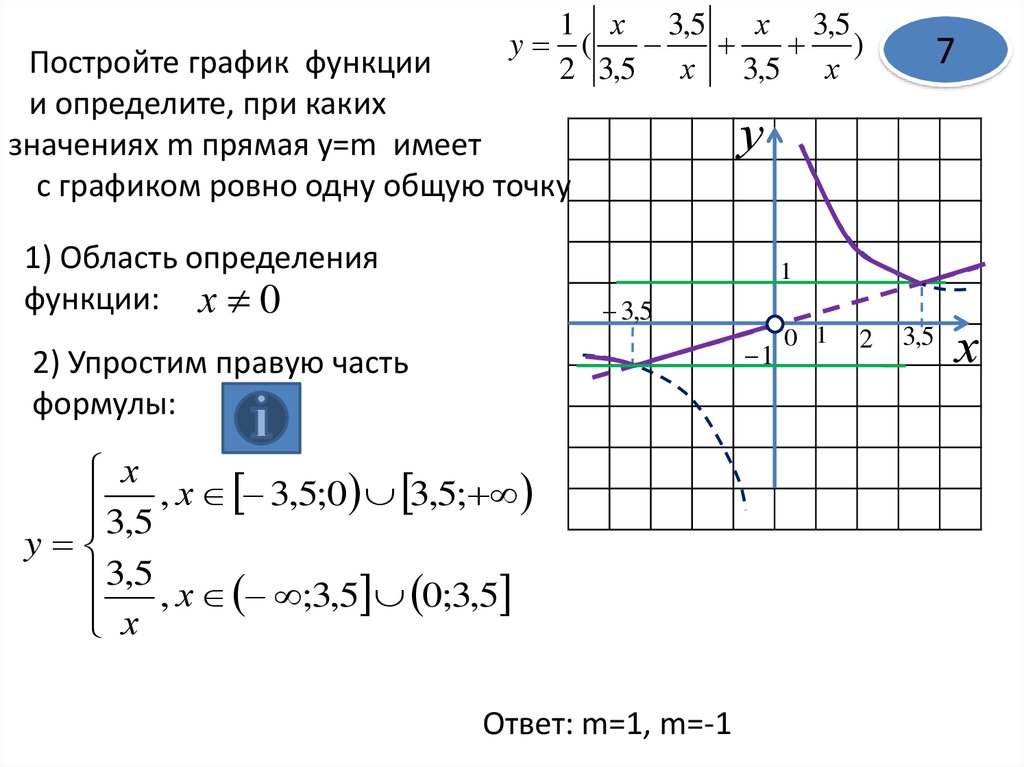
8.

1 х 3,5
х 3,5
y (
)
2 3,5 х 3,5 х
Постройте график функции
и определите, при каких
значениях m прямая y=m имеет
с графиком ровно одну общую точку
1) Область определения
функции: х 0
7
у
1
3,5
1
2) Упростим правую часть
формулы:
х
, х 3,5;0 3,5;
3,5
y
3,5 , х ;3,5 0;3,5
х
Ответ: m=1, m=-1
0 1
2
3,5
х

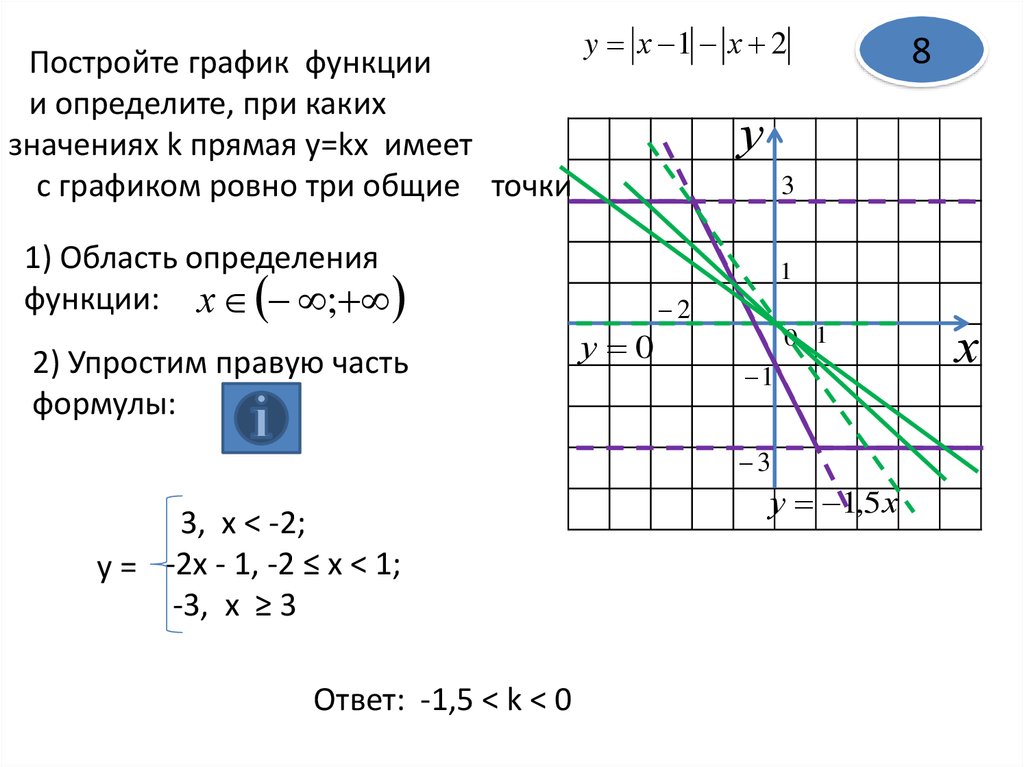
9.

Постройте график функции
и определите, при каких
значениях k прямая y=kx имеет
с графиком ровно три общие точки
y х 1 х 2
у
3
1) Область определения
функции: х ;
2) Упростим правую часть
формулы:
1
2
у 0
0 1
1
3
3, х < -2;
у = -2х - 1, -2 ≤ х < 1;
-3, х ≥ 3
Ответ: -1,5 < k < 0
8
у 1,5 х
х

10.

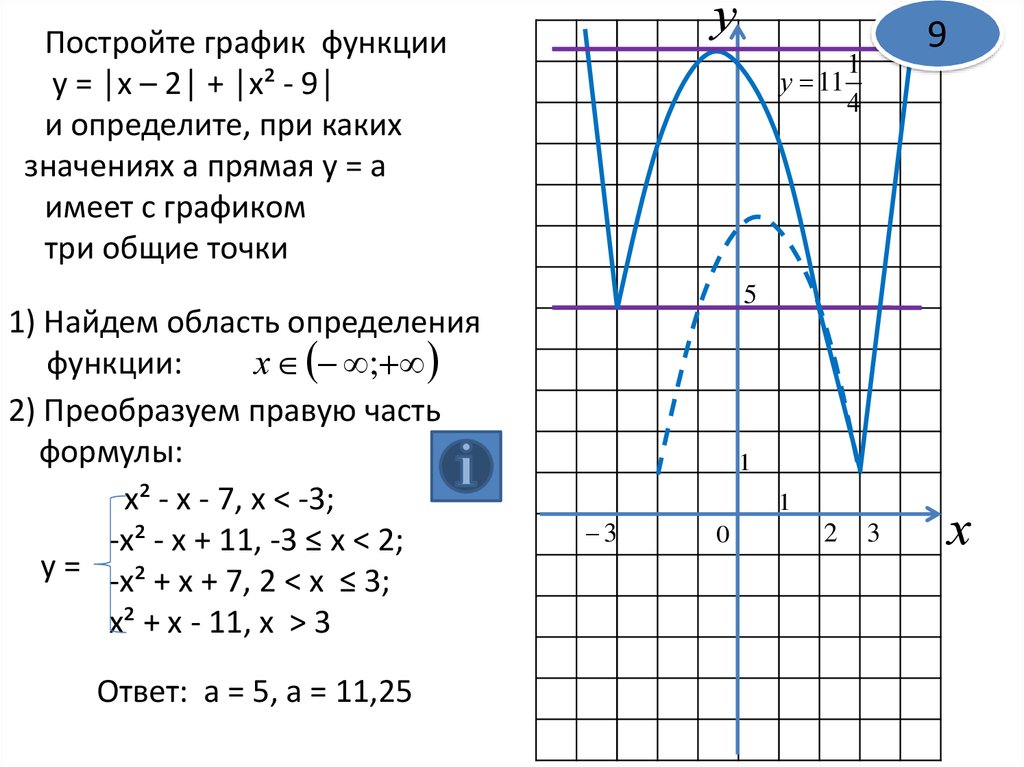
у
Постройте график функции
у = │х – 2│ + │х² - 9│
и определите, при каких
значениях а прямая y = а
имеет с графиком
три общие точки
1) Найдем область определения
функции:
х ;
2) Преобразуем правую часть
формулы:
х² - х - 7, х < -3;
-х² - х + 11, -3 ≤ х < 2;
у = -х² + х + 7, 2 < х ≤ 3;
х² + х - 11, х > 3
Ответ: а = 5, а = 11,25
у 11
9
1
4
5
1
3
1
0
2
3
х

11.