Семинар-сказка «В стране многоугольнии»

1. Семинар-сказка «В стране многоугольнии»

Цели урока:
Систематизировать основные свойства и
признаки четырёхугольников, их
определения и формулы вычисления
площадей;
Установить связь между основными
фигурами, изучаемыми в данной теме;

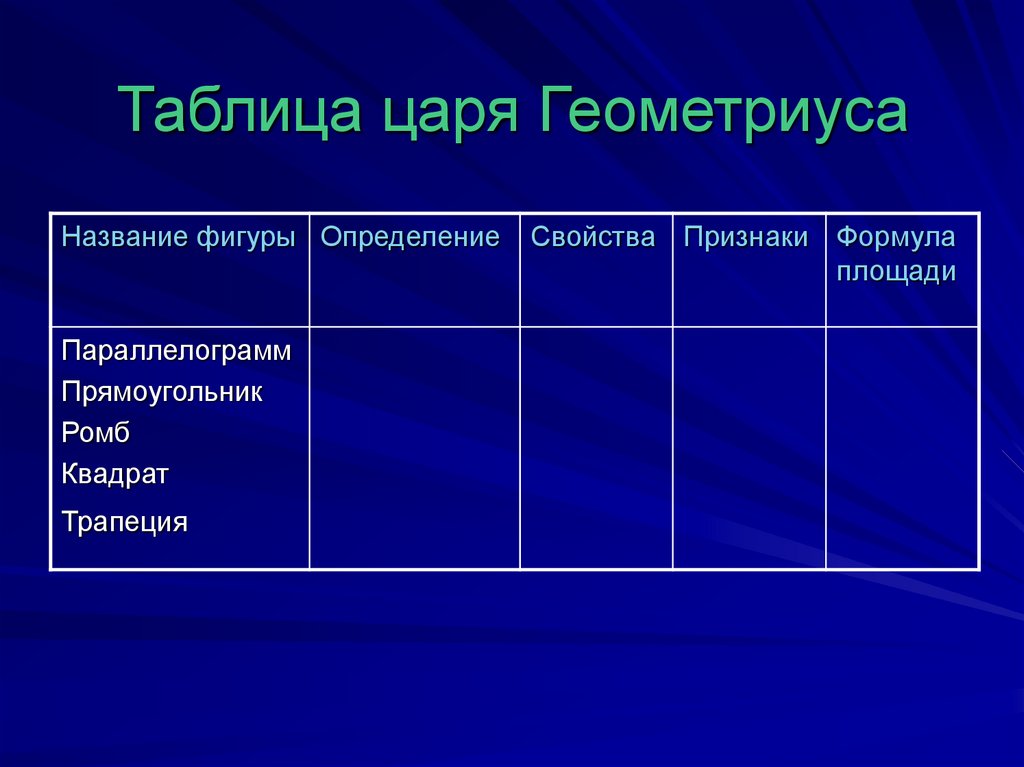
2. Таблица царя Геометриуса

Название фигуры Определение
Параллелограмм
Прямоугольник
Ромб
Квадрат
Трапеция
Свойства Признаки Формула
площади

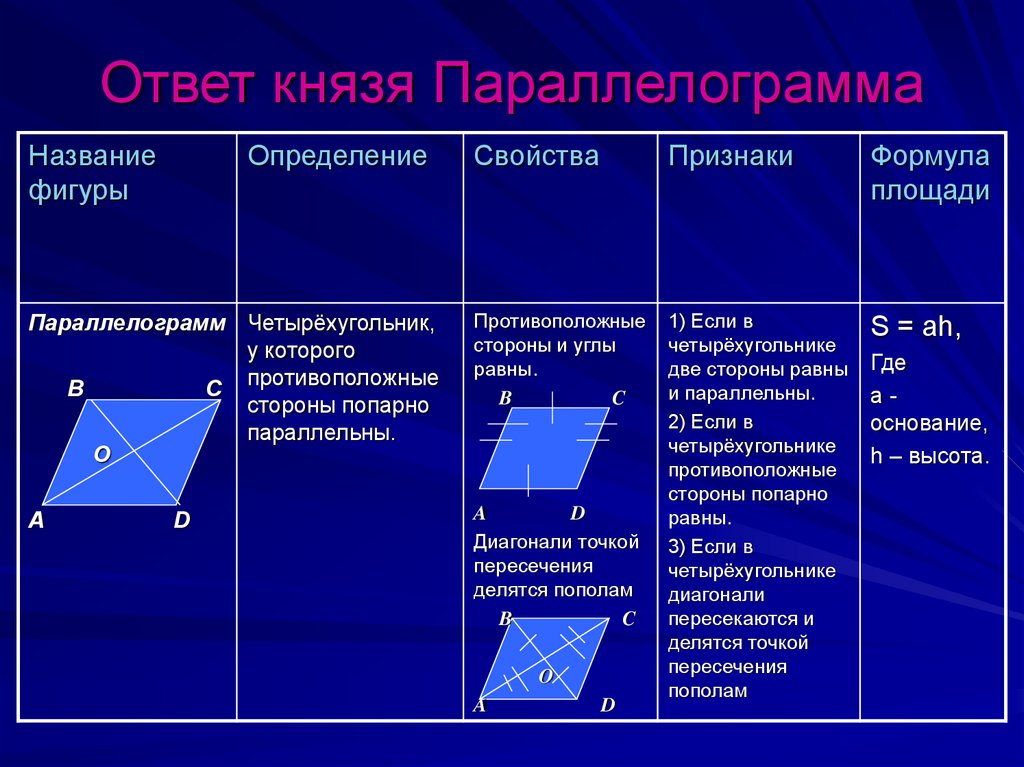
3. Ответ князя Параллелограмма

Название
фигуры
Определение
Свойства
Признаки
Формула
площади
Параллелограмм Четырёхугольник,
у которого
В
С противоположные
стороны попарно
параллельны.
O
Противоположные
стороны и углы
равны.
B
C
S = ah,
А
A
D
Диагонали точкой
пересечения
делятся пополам
B
C
1) Если в
четырёхугольнике
две стороны равны
и параллельны.
2) Если в
четырёхугольнике
противоположные
стороны попарно
равны.
3) Если в
четырёхугольнике
диагонали
пересекаются и
делятся точкой
пересечения
пополам
D
O
A
D
Где
аоснование,
h – высота.

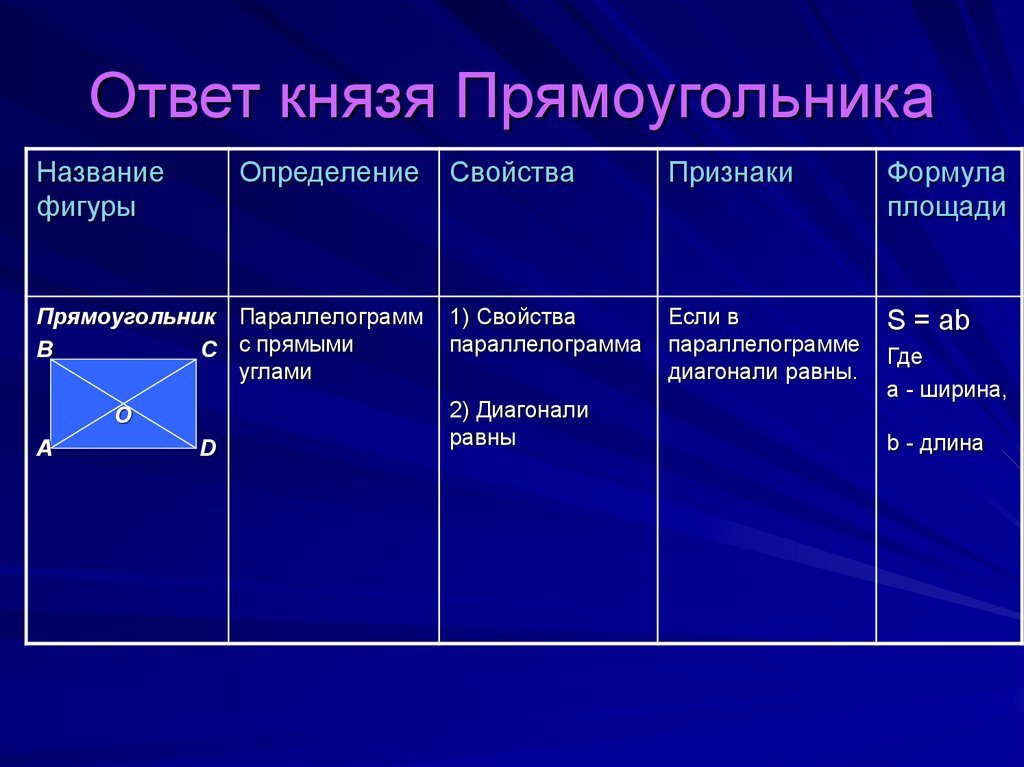
4. Ответ князя Прямоугольника

Название
фигуры
Определение
Прямоугольник Параллелограмм
B
C с прямыми
углами
O
A
D
Свойства
Признаки
Формула
площади
1) Свойства
параллелограмма
Если в
параллелограмме
диагонали равны.
S = ab
2) Диагонали
равны
Где
a - ширина,
b - длина

5. Ответ князя Ромба

Название
фигуры
Определение
Свойства
Признаки
Формула
площади
Ромб
В
Параллелограмм,
у которого
стороны равны.
1) Свойства
параллелограмма
Если в
параллелограмме
диагонали
взаимно
перпендикулярны
и делят его углы
пополам.
S = ah,
где
а - основание
h - высота.
A
O
D
С
2) Диагонали
взаимно
перпендикулярны,
точкой
пересечения
делятся пополам
и делят углы
пополам

6. Ответ князя Квадрата

Название
фигуры
Определение
Свойства
Признаки
Формула
площади
Квадрат
1) Ромб с
прямыми углами.
1) Все углы равны
1) Если в ромбе
диагонали равны.
S = а2 ,
B
C
2) Прямоугольник
с равными
сторонами.
O
A
D
2) Диагонали
квадрата равны,
взаимно
перпендикулярны,
точкой
пересечения
делятся пополам
и делят углы
пополам
2) Если в
прямоугольнике
диагонали
взаимно
перпендикулярны.
где
а – сторона.

7. Ответ царевны Трапеции

Название
фигуры
Определение
Свойства
Признаки
Формула
площади
Трапеция
B
C
Четырёхугольник,
у которого две
стороны
параллельны, а
две другие нет.
1) Если трапеция
равнобедренная,
то диагонали и
углы при
основаниях
равны.
Если в
четырёхугольнике
две стороны
параллельны.
S = mh,
A
D
2) Если трапеция
прямоугольная,
то одна из
боковых сторон
перпендикулярна
основаниям.
где
m - средняя
линия,
h – высота.

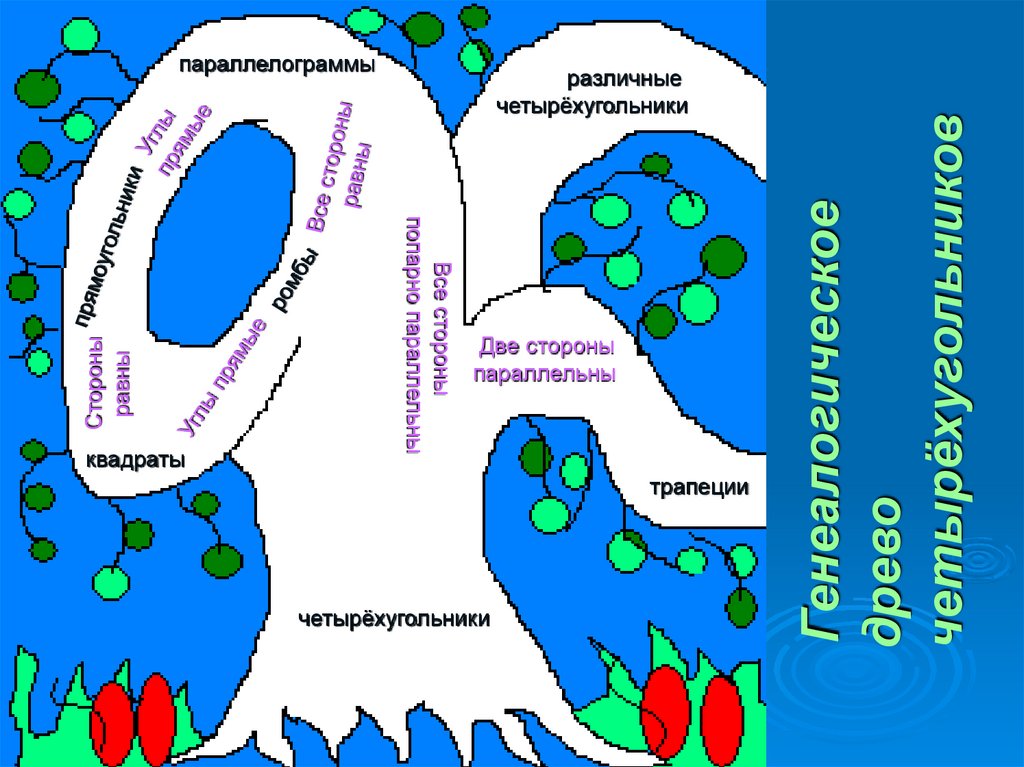
8. различные четырёхугольники

Две стороны
параллельны
трапеции
четырёхугольники
Генеалогическое
древо
четырёхугольников
квадраты
различные
четырёхугольники
Все стороны
попарно параллельны
Стороны
равны
параллелограммы