Similar presentations:
Антенные решетки. (Лекция 7)
1. Антенные решетки
Лекция 72.
Множитель системы линейной решеткиДискретные системы состоящие из ряда отдельных
излучателей (элементов), представляющие
идентичные одинаково ориентированные
излучатели.
Рассмотрим линейную решетку
Анализ множителя решетки:
- расстояние между элементами одинаковы (эквидистантные решетки).
- амплитуды токов в излучателях одинаковы
-фаза тока от излучателя к излучателю изменяется на постоянную
величину
равномерная прямофазная решетка
3.
-обобщенный угол
Используя формулу для суммы членов геометрической прогрессии
Получим
фазовая диаграмма
Система излучает сферическую волну. Фазовый центр системы
находится в середине.
4.
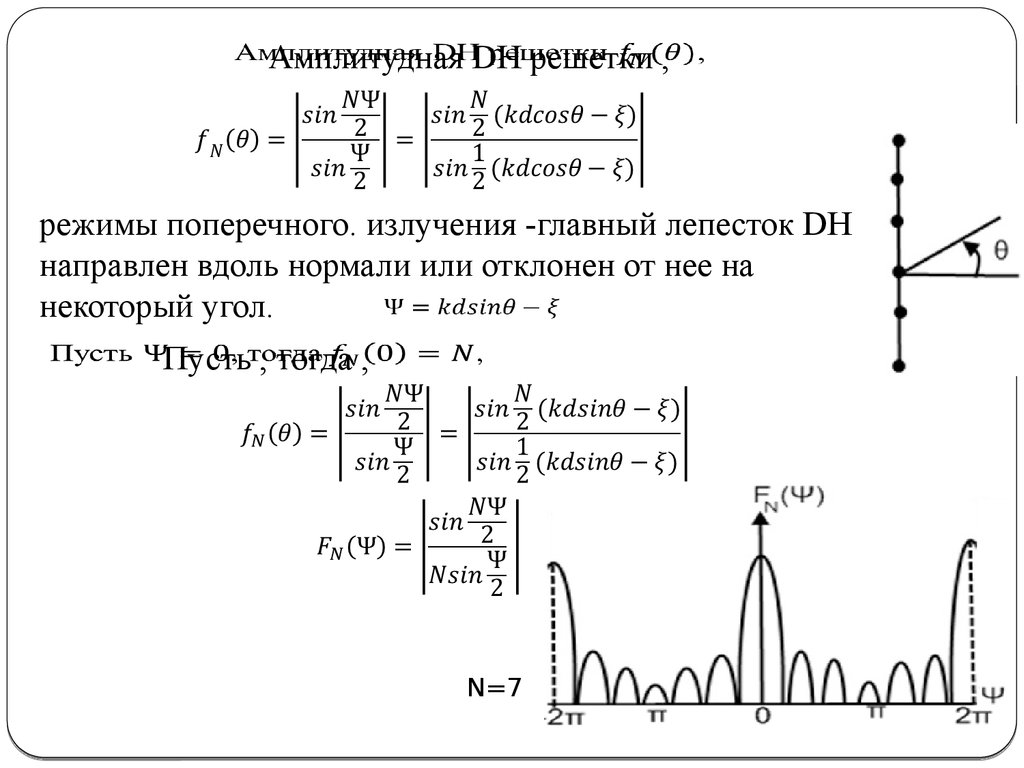
Амплитудная DH решетки ,
режимы поперечного. излучения -главный лепесток DH
направлен вдоль нормали или отклонен от нее на
некоторый угол.
Пусть , тогда ,
N=7
5.
-
периодическая
функция (
m=0
нулевой (центральный, главный);
m=1-максиму первого порядка, дифракционный
При n<<N можно положить sin
реальный
угол ∊- ,
рабочая область (область видимости) kd-
6.
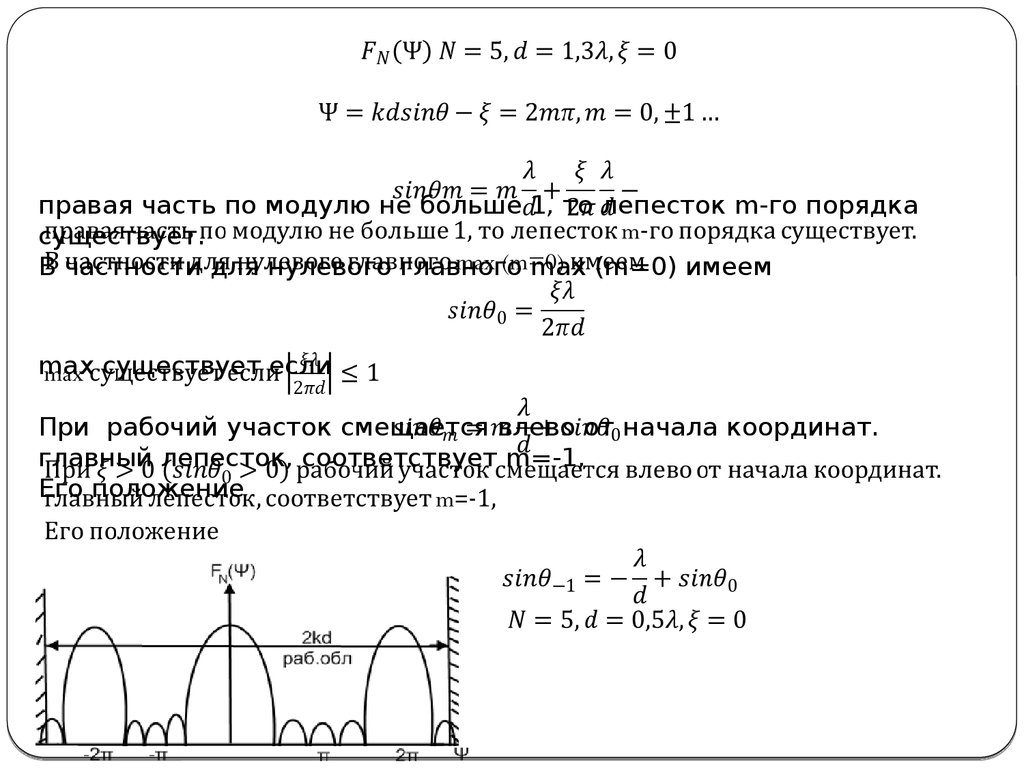
правая часть по модулю не больше 1, то лепесток m-го порядка
существует.
В частности для нулевого главного max (m=0) имеем
max существует если
При рабочий участок смещается влево от начала координат.
главный лепесток, соответствует m=-1,
Его положение
7.
Решетки со спадающим АРпри N>>1 в равномерном АР (, с УБЛ Fб1≈22%.
При cos-м АР ( , а Fб1≈7%.
Главный лепесток становиться ассиметричным и расширяется.
Если решетка имеет несколько главных max, это приводит к
уменьшению КНД антенны, возникновению ложного пеленга,
снижению помехозащищенности системы.
8.
Условие единственности главного лепесткаВыполнение условия для m-го лепестка
m=-1 и m=±1 главных лепестков это условие не выполнялось, т.е.
Если , то труднее обеспечить выполнение неравенства (20б),
если ,
условие единственности m-го лепестка.
Допустимые расстояния между элементами решетки:
- для синфазной решетки
(sin
- для решетки осевого излучения
()
-переход к неэквидистантным решеткам
9.
Неэквидистантные решеткиРасстояния между излучателями неодинаковы. DH решеток
имеет лишь единичный максимум.
Разность хода лучей от 2x соседних излучателей
=dsin
Если d>λ, →(), т.е. поле этих излучений в направлении ,
складывается в фазе
Угол находится из условия
в направлении
Если → () «размазывание» дифр-х max.
«разряженные»
решетки-зависит от L и мало чувствительна к
степени заполнения апертуры.
«разрежение» решетки сопровождается ↑ среднего уровня боковых
лепестков. УБЛ~ обратно числу оставшихся в решетке излучателей.
в неэкв.решетки> эквид. решетки
10.
КНДL
в режиме поперечного и наклонного излучений
в режиме осевого излучения
в режиме осевого излучения c оптимально замедленной фазовой
скоростью
Неэквидистанные решетки используют в качестве приемных,т.к
• имеют большие размеры.
• число элементов N оказывается при эквидистантном их
расположении значительнее большими.
Использование неэквидистантных разреженных решеток
представляется особенно перспективным.








 physics
physics








