Мінімізація скінченного автомата. (Тема 5)

1. Тема 5: Мінімізація скінченного автомата

1. Основні означення і поняття
2. Алгоритм вилучення недосяжних станів скінченног
о автомата
3. Мінімізація скінченного автомата за допомогою поб
удови класів еквівалентності
4. Функція переходів і розширена (узагальнена) функ
ція переходів недетермінованого скінченного автомат
а
5. Мінімізація скінченного автомата за допомогою таб
лиці нееквівалентних станів

2. 1. Основні означення і поняття

Нехай ми маємо автомат: M (Q, , , q0 , F ) q1 q 2 , q1 , q 2 Q.
Означення 1. Кажуть, що ланцюжок x * розрізняє стани
q1 і q 2 , якщо із стану q1 по x можна перейти в q3 , а з q 2 по x
можна перейти в q 4 , причому q3 F , q4 F або q3 F , q4 F .
Якщо ланцюжок x такий, що ( q1 , x ) k ( q3 , e), ( q2 , x ) k ( q4 , e) ,
то ланцюжок x довжиною k розрізняє ці стани.
Означення 2. Кажуть, що стани q1 , q 2 k-не розрізняються:
q1 k q 2 , якщо не існує ланцюжка x * , x k . , який розрізняє ці
стани.
Означення 3. Будемо говорити, що q1 , q 2 не розрізняються
(є еквівалентними) і писати q1 q 2 , якщо вони k -не
розрізняються для k N .
Означення 4. Стан q називається недосяжним, якщо не
існує вхідного ланцюжка x * : (q 0 , x) * (q, e).
зведеним
Означення
5.
Автомат
M
називається
(мінімальним), якщо в Q немає недосяжних станів і немає двох
станів, що не розрізняються.

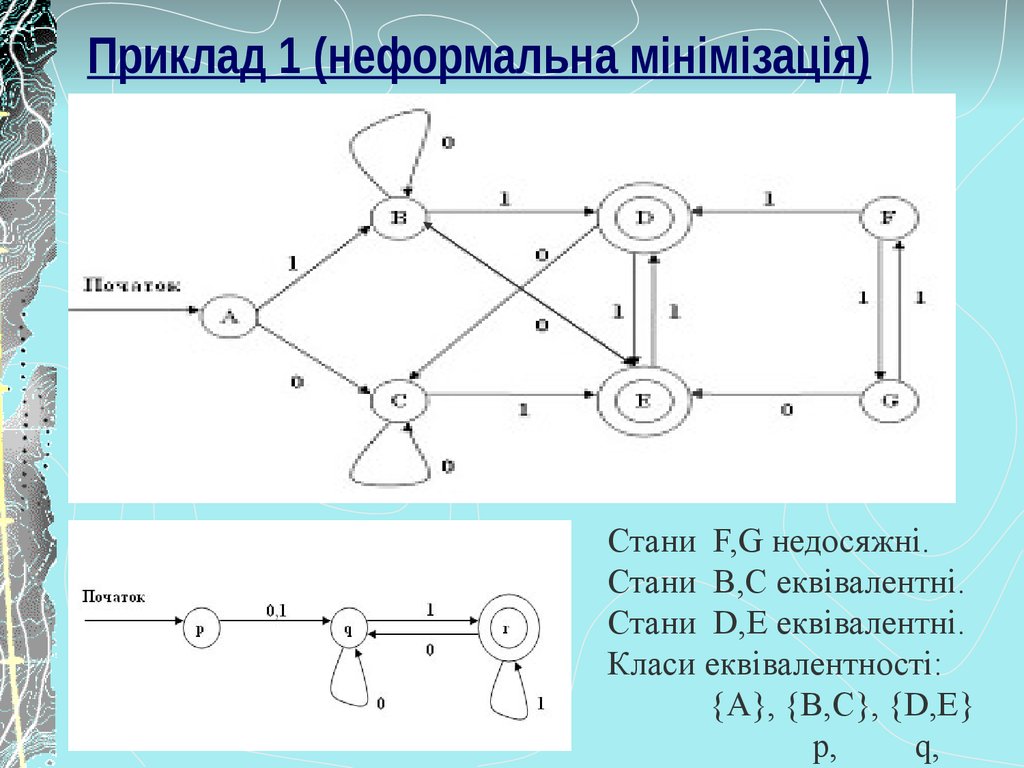
3. Приклад 1 (неформальна мінімізація)

Стани F,G недосяжні.
Стани B,C еквівалентні.
Стани D,E еквівалентні.
Класи еквівалентності:
{A}, {B,C}, {D,E}
p,
q,

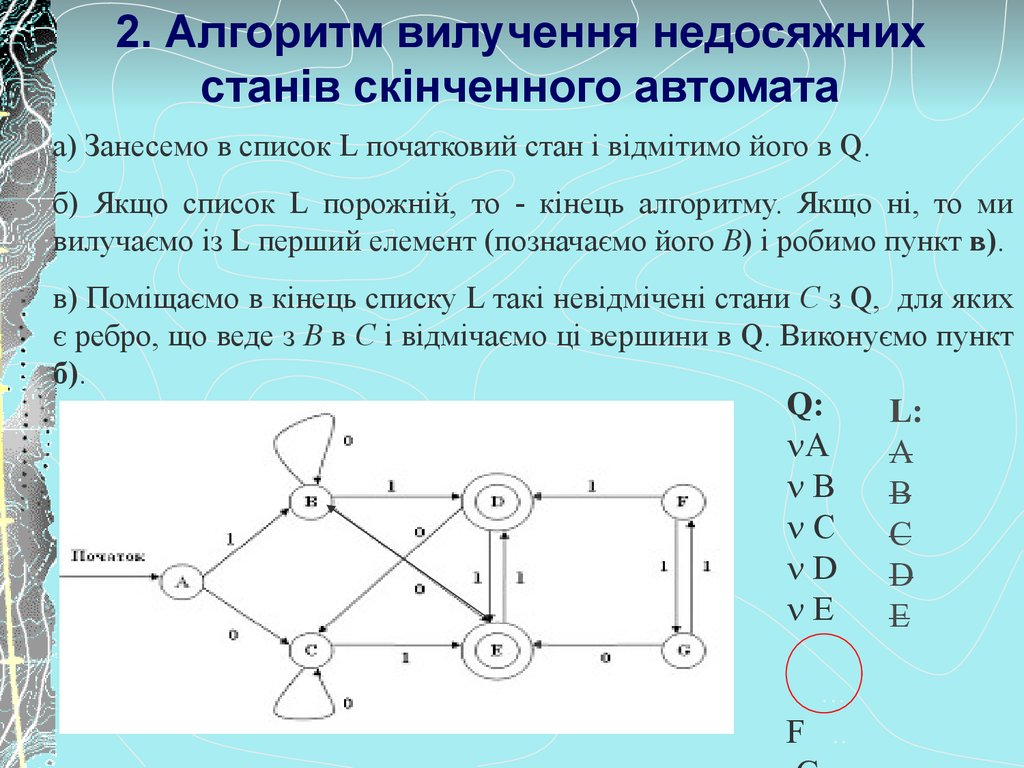
4. 2. Алгоритм вилучення недосяжних станів скінченного автомата

а) Занесемо в список L початковий стан і відмітимо його в Q.
б) Якщо список L порожній, то - кінець алгоритму. Якщо ні, то ми
вилучаємо із L перший елемент (позначаємо його B) і робимо пункт в).
в) Поміщаємо в кінець списку L такі невідмічені стани C з Q, для яких
є ребро, що веде з B в C і відмічаємо ці вершини в Q. Виконуємо пункт
б).
Q:
A
B
C
D
E
...
F ..

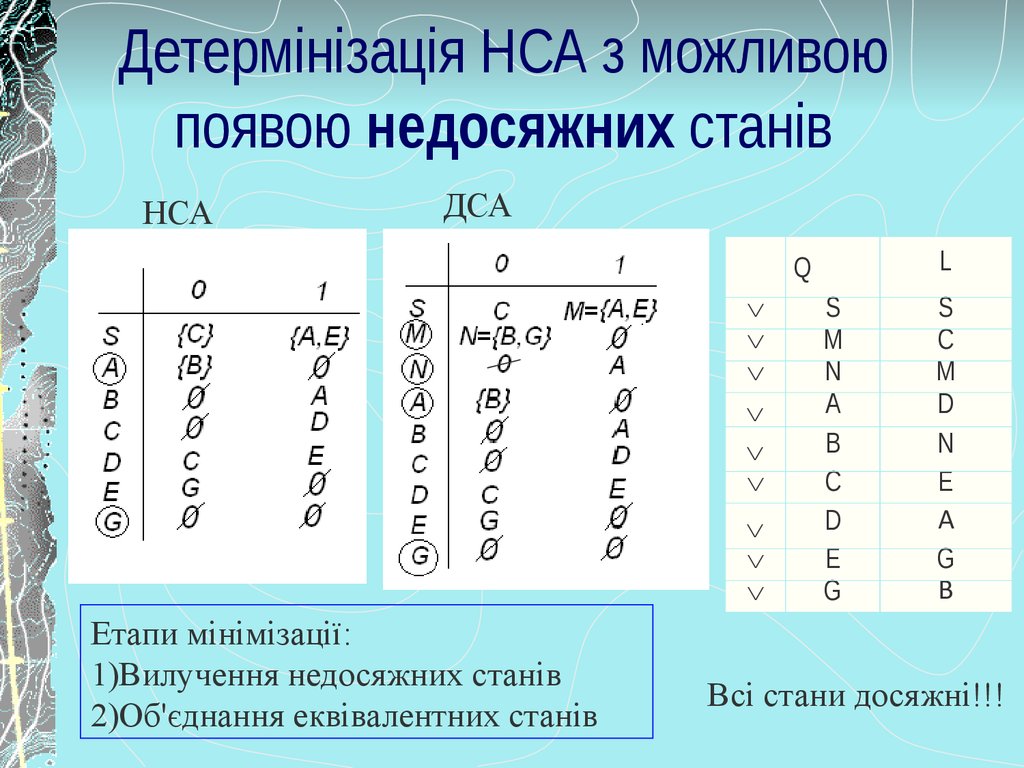
5. Детермінізація НСА з можливою появою недосяжних станів

НСА
ДСА
L
Q
Етапи мінімізації:
1)Вилучення недосяжних станів
2)Об'єднання еквівалентних станів
S
M
N
A
B
C
D
E
G
S
C
M
D
N
E
A
G
B
Всі стани досяжні!!!

6. 3. Мінімізація скінченного автомата за допомогою побудови класів еквівалентності

Для довільних двох станів q1 , q 2 Q
можна записати таке:
3.
Мінімізація скінченного автомата за
- q1 0 q 2 , якщо q1 , q 2 F або q1 , q 2 F .
допомогою побудови класів
( q1 , q2 0 – не розрізняються)
- q1 k q 2 , якщо q1 k 1 q2 , ( q1 , a ) k 1 ( q2 , a ), еквівалентності
a .
( q1 , q2 k-не розрізняються)
Алгоритм мінімізації
I. Побудуємо відношення 0 . Це відношення розбиває
множину Q на два класи еквівалентності: F - множина
заключних станів, Q \ F - множина незаключних станів.
q1 0 q 2 означає, що {q1 , q 2 } F або {q1 , q 2 } Q \ F .
II. Будуємо відношення 1 . Це відношення розбиває попередні
класи еквівалентності на нові класи еквівалентності. Два
стани належать одному класу еквівалентності для
відношення 1 , якщо вони раніше належали одному класу
еквівалентності і ланцюжок довжиною 1 не може розрізнити
стани q1 , q 2 .

7.

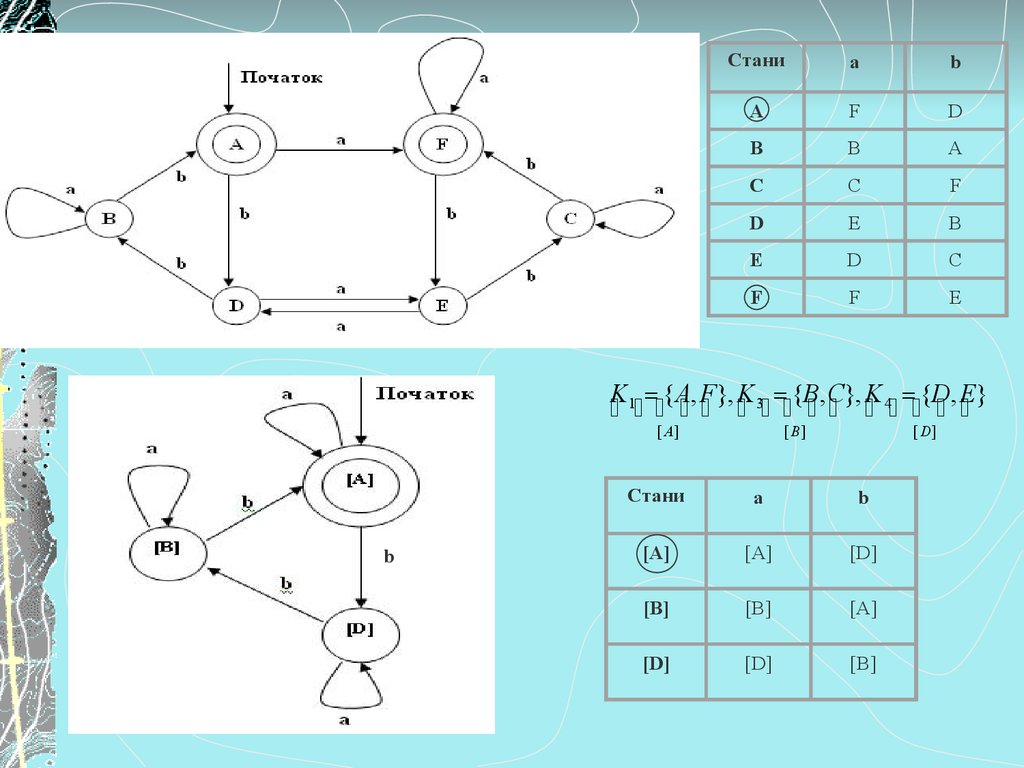
8. Приклад 2. Мінімізації скінченного автомата методом побудови класів еквівалентності (метод 1.1)

Cтани
a
b
A
F
D
B
B
A
C
C
F
D
E
B
E
D
C
F
F
E
L: A,F,D,E,B,C
I. Будуємо відношення еквівалентності 0 : K1 { A, F }, K 2 {B, C , D, E}.
II. Будуємо відношення еквівалентності 1 .
K1 :
не розрізнив стани класу
( A, a ) F , ( F , a ) F Символ а
( A, b) D, ( F , b) E еквівалентності K1, символ b – також.
A 1 F

9.

Cтани
a
b
A
F
D
K 2 {B, C , D, E} :
B
B
A
C
C
F
D
E
B
( B , a ) B , (C , a ) C , ( D , a ) E , ( E , a ) D
( B, b) A, (C , b) F , ( D, b) B, ( E , b) C
E
D
C
F
F
E
II. Будуємо відношення еквівалентності
Класи еквівалентності 1 :
K1 { A, F }, K 3 {B, C}, K 4 {D, E}
1 .
B 1 C , D 1 E
Символ а не розрізнив стани
класу еквівалентності К2, символ
b – розрізнив. К2 розділяється на
два класи: K3={B,C}, K4={D,E}
III. Будуємо відношення еквівалентності
2 : K1 :
A 2 F , B 2 C , D 2 E
Класи еквівалентності 2 :
K1 { A, F }, K 3 {B, C}, K 4 {D, E}
Далі розрізнити класи K1 , K 3 , K 4 неможливо.
( A, a ) F , ( F , a ) F
( A, b) D, ( F , b) E
K3 :
( B, a ) B, (C , a ) C
( B, b) A, (C , b) F
K4 :
( D, a ) E , ( E , a ) D
( D, b) B, ( E , b) C

10.

Cтани
a
b
A
F
D
B
B
A
C
C
F
D
E
B
E
D
C
F
F
E
K { A, F }, K {B, C}, K {D, E}
1 3 4
[ A]
b
[ D]
[B]
Стани
a
b
[A]
[A]
[D]
[B]
[B]
[A]
[D]
[D]
[B]

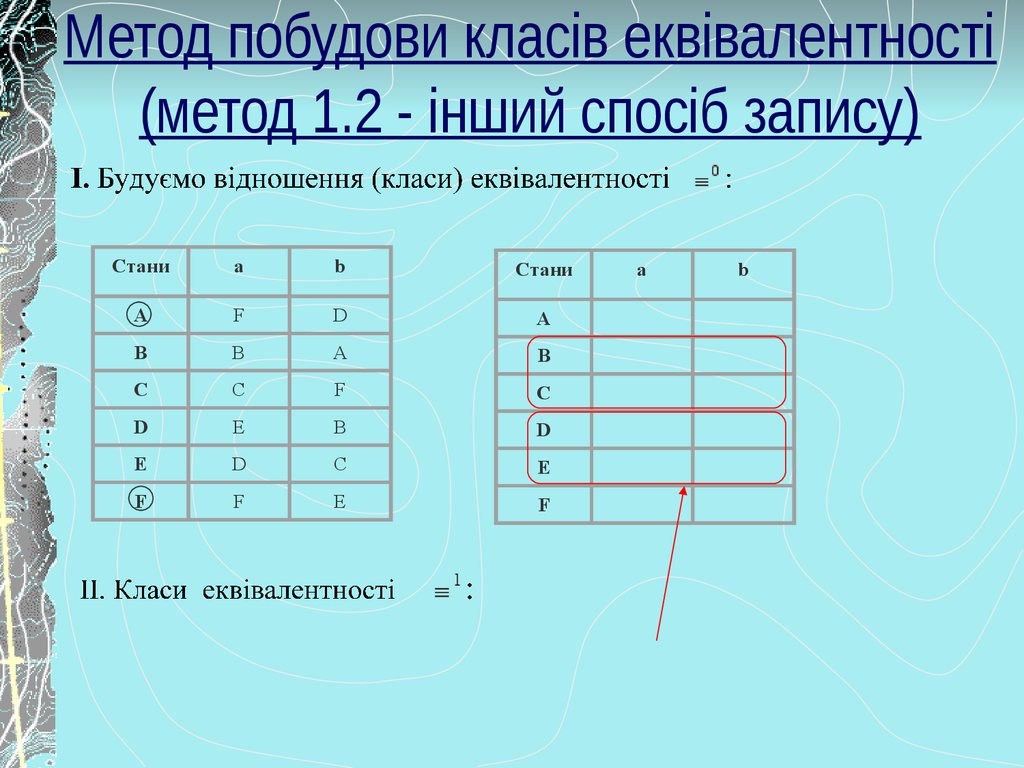
11. Метод побудови класів еквівалентності (метод 1.2 - інший спосіб запису)

Cтани
a
b
Cтани
A
F
D
A
B
B
A
B
C
C
F
C
D
E
B
D
E
D
C
E
F
F
E
F
a
b

12.

Cтани
a
b
Cтани
A
F
D
A
B
B
A
B
C
C
F
C
D
E
B
D
E
D
C
E
F
F
E
F
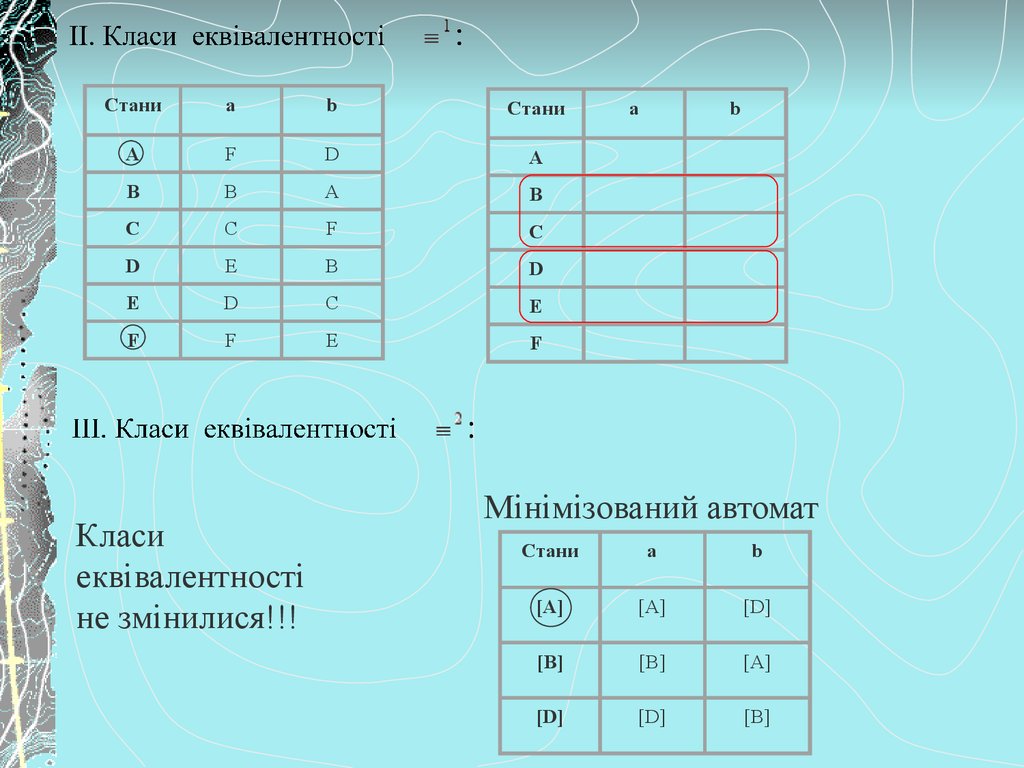
Класи
еквівалентності
не змінилися!!!
a
b
Мінімізований автомат
Стани
a
b
[A]
[A]
[D]
[B]
[B]
[A]
[D]
[D]
[B]

13. 4. Функція переходів і розширена (узагальнена) функція переходів недетермінованого скінченного автомата

14. Приклад 3 (для НСА)

Автомат, який
дозволяє ланцюжки,
що закінчуються на 01
Розглянемо ланцюжок 00101. Альтернативи:
ˆ(q0 ,001) {q 0 , q 2 }
ˆ(q ,00) {q , q }
0
0
1

15. Рекурсивний алгоритм побудови розширеної функції переходів

ˆ (q, e) {q}
ˆ(q, xa) ( ˆ(q, x), a)
xa, , x , a
*
*
ˆ(qх, ) {p 1 ,p 2 ,...,p k }
k
( p , a ) {r , r ,..., r }
i
i 1
ˆ (q, ) {r1 , r2 ,..., rm }
1
k
2
m
ˆ(q, ) ( pi , a)
i 1

16. Приклад обчислення розширеної функції переходів для ДСА

ˆ (q, e) {q}
ˆ(q, xa) ( ˆ(q, x), a)

17. Приклад 3 (продовження)

ˆ (q, e) {q}
ˆ(q, xa) ( ˆ(q, x), a)
НСА
k
ˆ(q, ) ( pi , a)
i 1
Розглянемо ланцюжок 00101. Побудова функції переходів
за алгоритмом:

18. 5. Мінімізація скінченного автомата за допомогою таблиці нееквівалентних станів

19. Схема алгоритму:

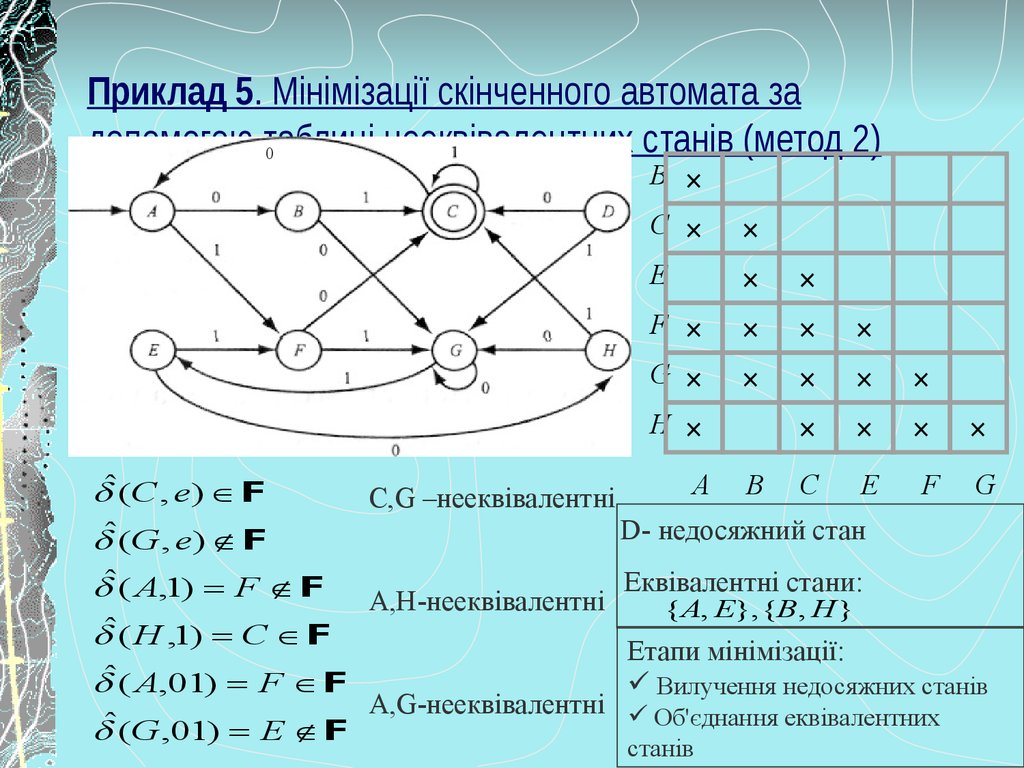
20. Приклад 5. Мінімізації скінченного автомата за допомогою таблиці нееквівалентних станів (метод 2)

0
B
C
E
F
G
С
Е
F
G
H
ˆ (C , e) F
С,G –нееквівалентні
А
В
ˆ (G , e) F
D- недосяжний стан
ˆ ( A,1) F F
Еквівалентні стани:
ˆ ( H ,1) C F
ˆ ( A,01) F F
ˆ (G ,01) E F
A,H-нееквівалентні
{ A, E}, {B, H }
Етапи мінімізації:
Вилучення недосяжних станів
A,G-нееквівалентні Об'єднання еквівалентних
станів

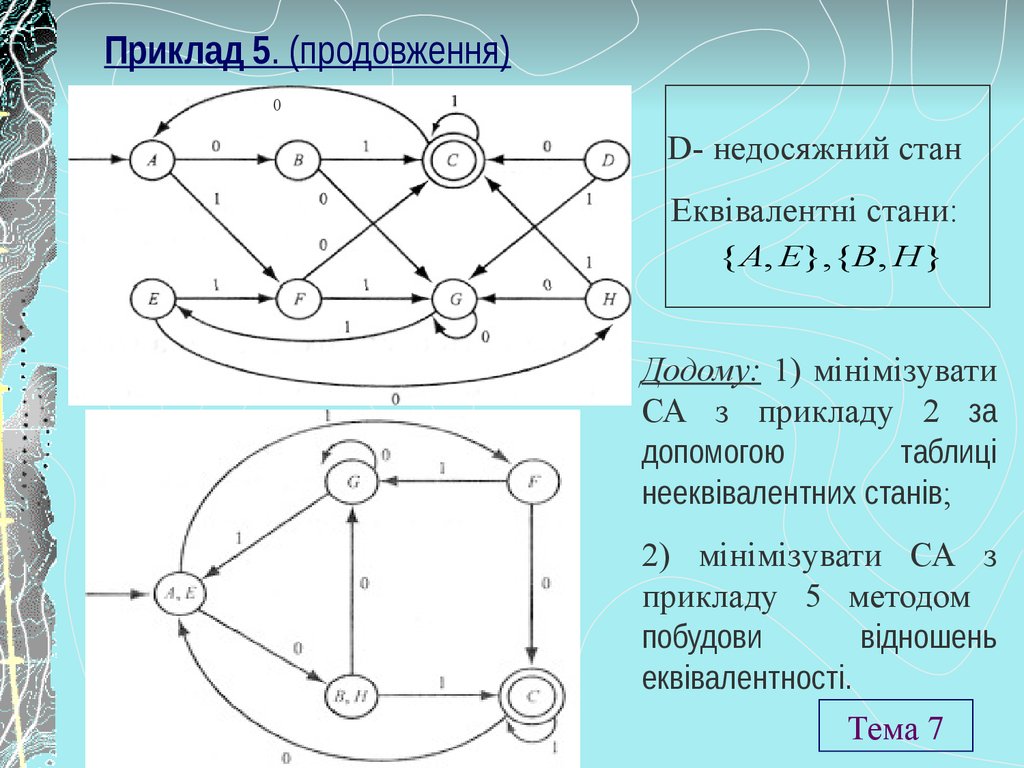
21. Приклад 5. (продовження)

0
D- недосяжний стан
Еквівалентні стани:
{ A, E}, {B, H }
Додому: 1) мінімізувати
СА з прикладу 2 за
допомогою
таблиці
нееквівалентних станів;
2) мінімізувати СА з
прикладу 5 методом
побудови
відношень
еквівалентності.
Тема 7