Similar presentations:
Решение треугольников
1. Решение треугольников Автор – учитель математики Фильчакова Е.М.
2. Т и п о в ы е з а д а ч и
Типовыезадачи
Решить
треугольник
по
двум сторонам
и углу
между ними
стороне и
прилежащим к
ней углам
трем сторонам
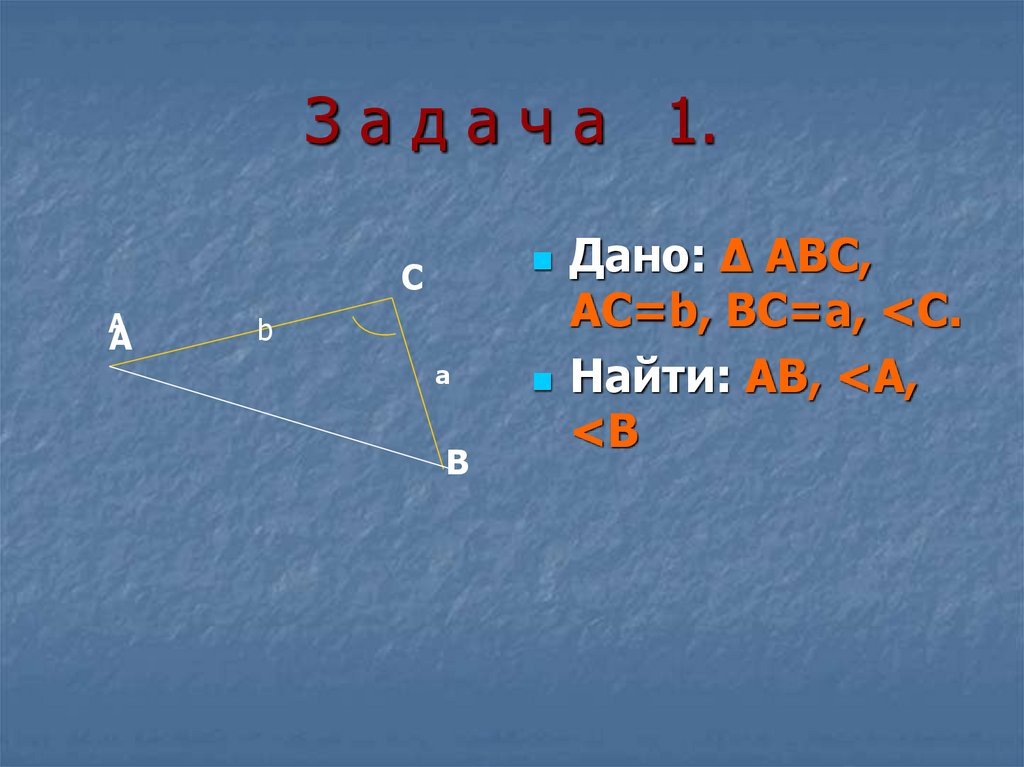
3. З а д а ч а 1.
СА
А
b
a
В
Дано: ∆ АВС,
АС=b, ВС=a, <С.
Найти: АВ, <А,
<В
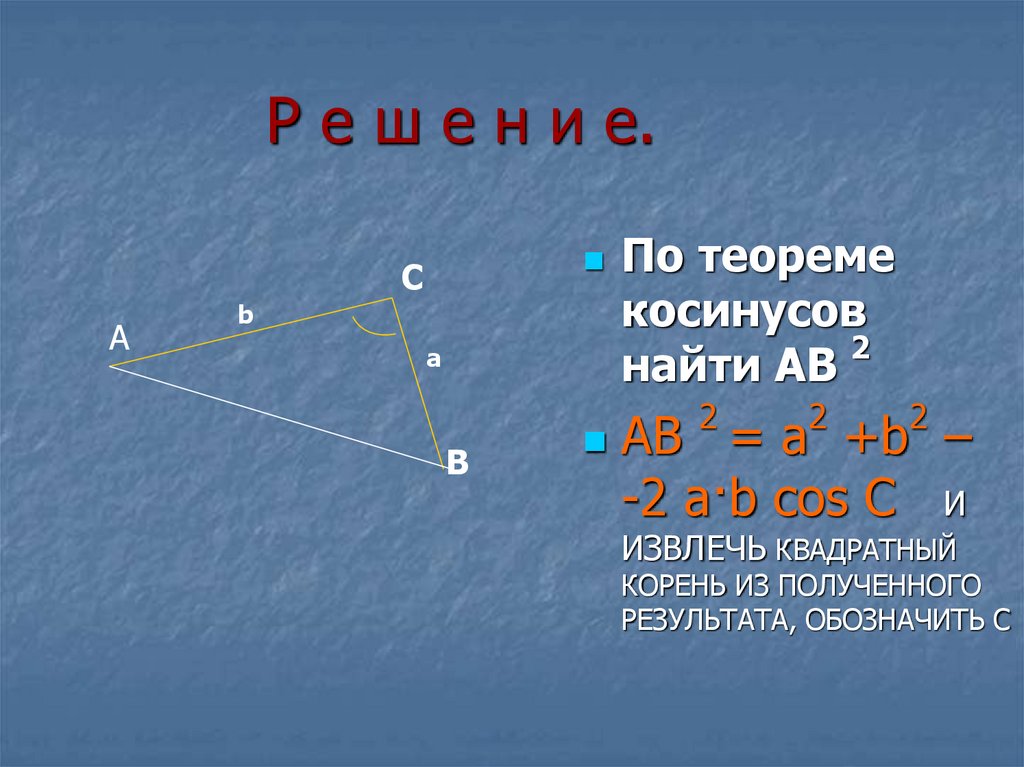
4. Р е ш е н и е.
СА
b
a
В
По теореме
косинусов
2
найти АВ
2
2
2
АВ = a +b –
-2 a·b cos С И
ИЗВЛЕЧЬ КВАДРАТНЫЙ
КОРЕНЬ ИЗ ПОЛУЧЕННОГО
РЕЗУЛЬТАТА, ОБОЗНАЧИТЬ C
5. Используя теорему косинусов, найти cos A
Аb
С
2
COS A=
2
2
(b + c – a )/(2b·c)
a
В
по найденному
значению
косинуса найти
<А
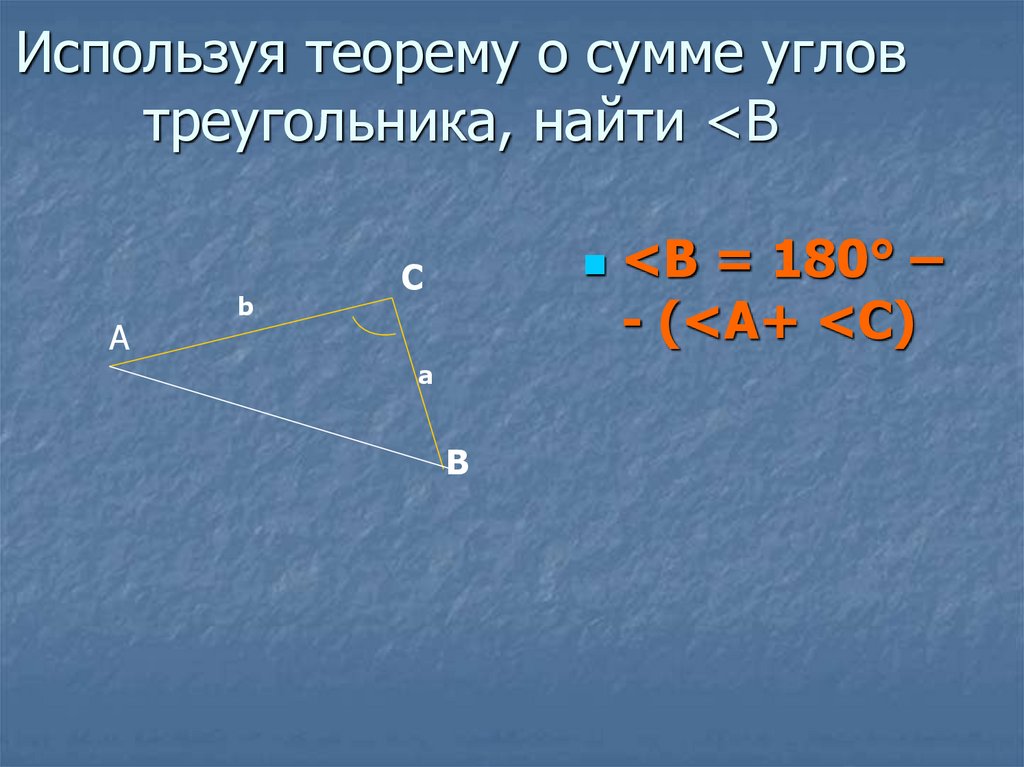
6. Используя теорему о сумме углов треугольника, найти <В
Используя теорему о сумме угловтреугольника, найти <В
А
b
С
a
В
<В = 180° –
- (<А+ <С)
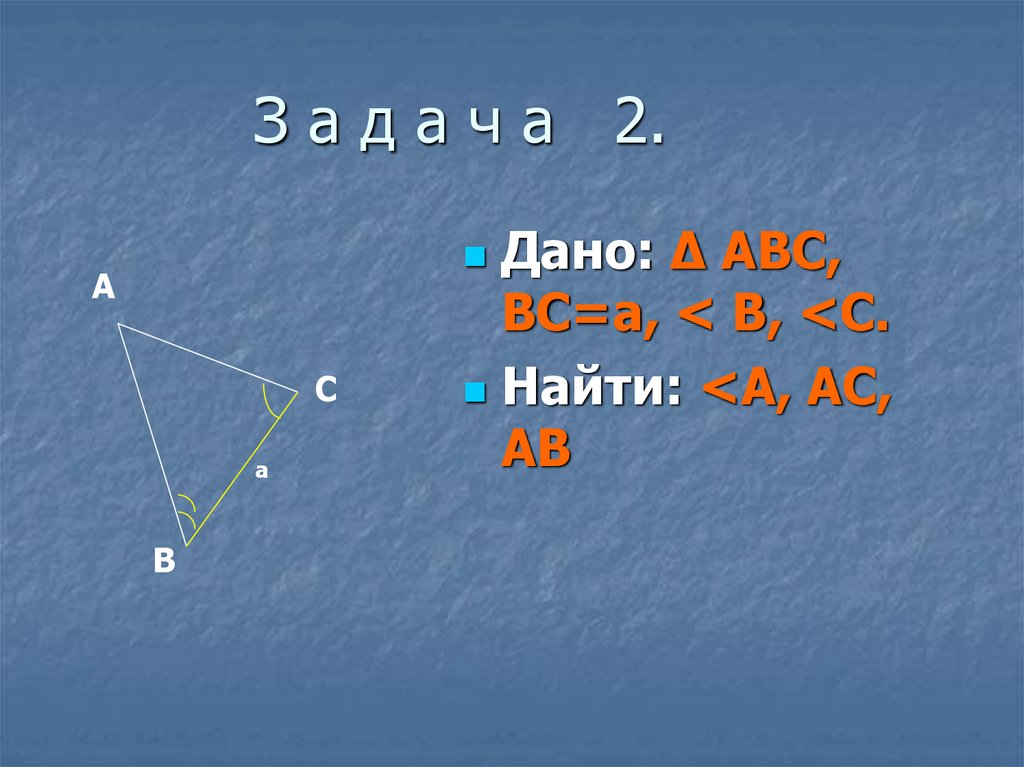
7. З а д а ч а 2.
Дано: ∆ АВС,ВС=a, < В, <С.
Найти: <А, АС,
АВ
А
С
a
В
8. Р Е Ш Е Н И Е
РЕШЕНИЕПО
ТЕОРЕМЕ О СУММЕ УГЛОВ
ТРЕУГОЛЬНИКА НАЙТИ <А
А
С
a
В
<А = 180° - (<В+ <С)
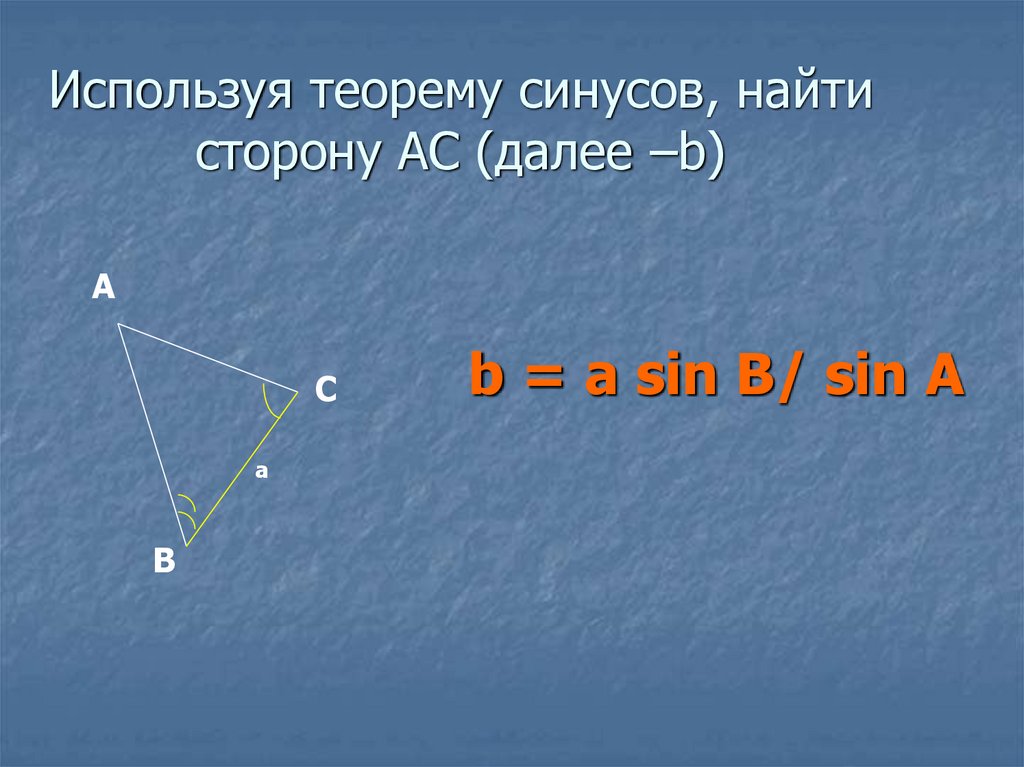
9. Используя теорему синусов, найти сторону АС (далее –b)
АС
a
В
b = a sin B/ sin A
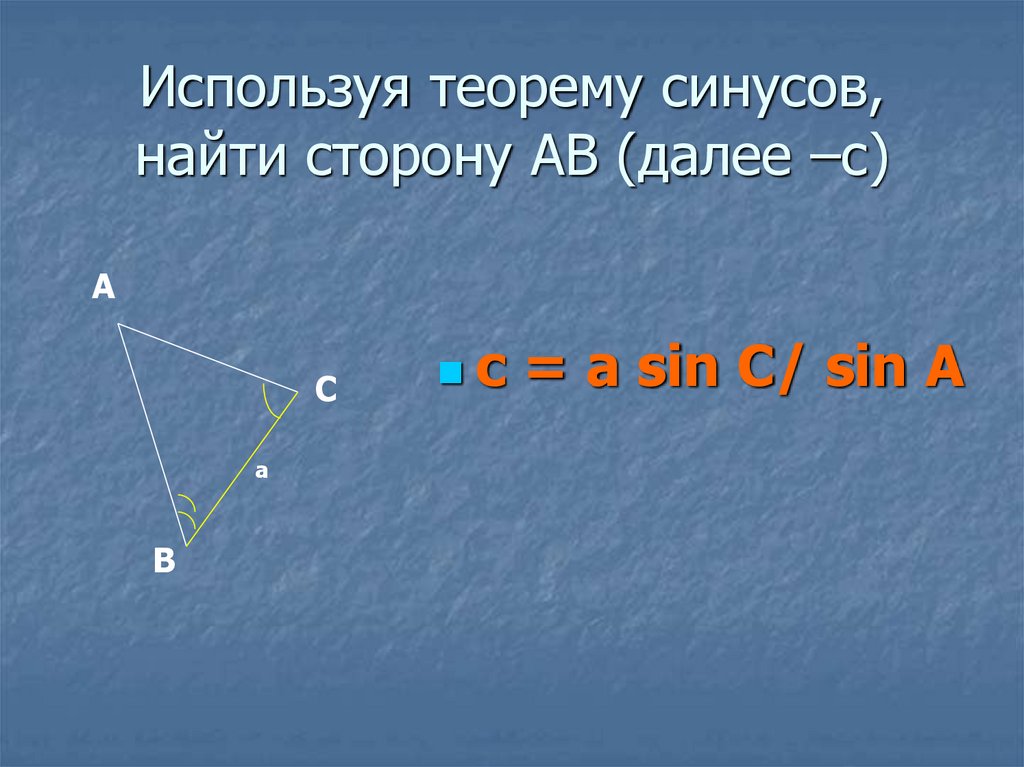
10. Используя теорему синусов, найти сторону АВ (далее –с)
АС
a
В
c
= a sin C/ sin A
11. З А Д А Ч А 3.
Аc
в
ДАНО: ∆ АВС,
ВС=a, АС=b,
АВ= с
Найти: <А,
<В, <С
b
a
с
12. Р е ш е н и е
РешениеИспользуя теорему косинусов,
А
найти cos A
c
в
b
a
с
COS A=
2
2
2
(b + c – a )/(2b·c)
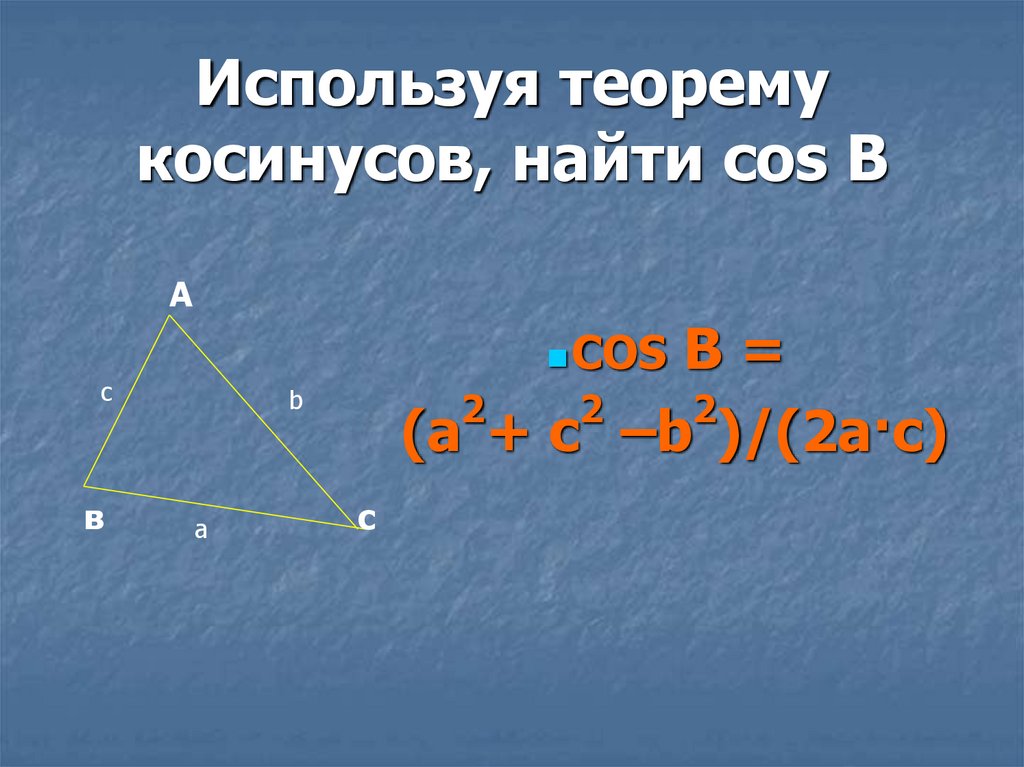
13. Используя теорему косинусов, найти cos В
Аc
в
В=
2
2
2
(a + c –b )/(2a·c)
COS
b
a
с
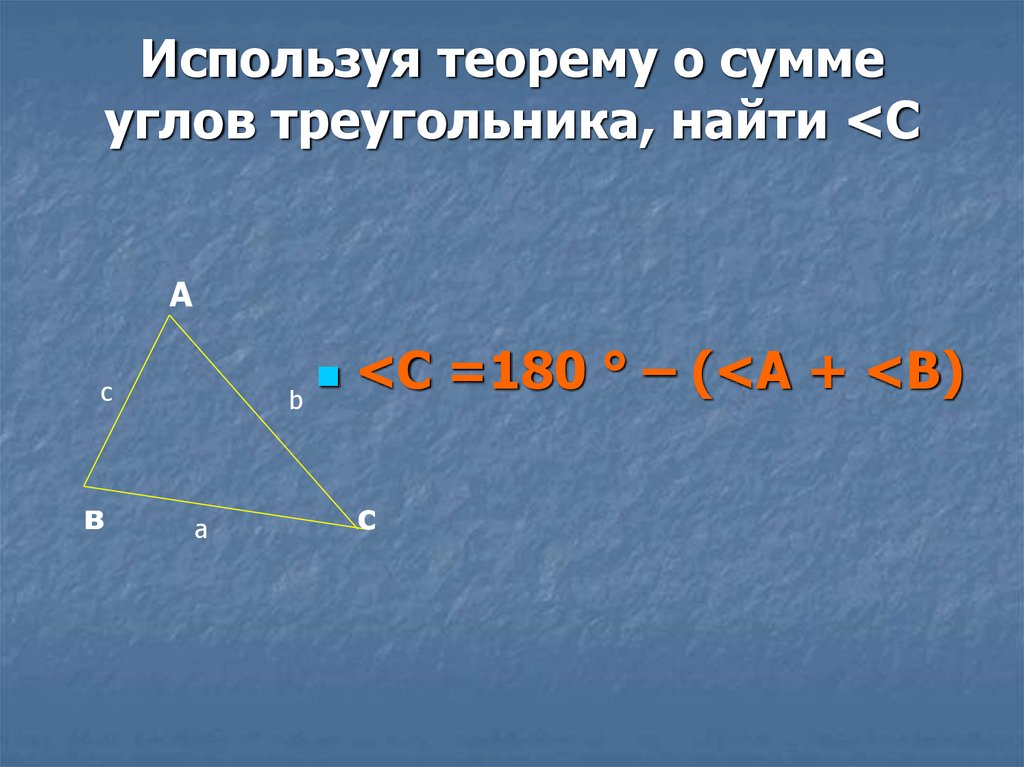
14. Используя теорему о сумме углов треугольника, найти <С
Используя теорему о суммеуглов треугольника, найти <С
А
c
в
b
a
<С =180 ° – (<А + <В)
с
15. З А М Е Ч А Н И Е
ЗАМЕЧАНИЕУГЛЫ ИЗМЕРЯЮТСЯ НИ ТОЛЬКО В
ГРАДУСАХ, НО И В РАДИАНАХ
180 ° = П РАДИАН, 1°= (П/ 180) РАДИАН
1
РАДИАН = (180
/ П) °
НАХОЖДЕНИЕ УГЛА ПО ЗНАЧЕНИЮ ЕГО
КОСИНУСА ЯВЛЯЕТСЯ ВЫЧИСЛЕНИЕМ
ОБРАТНОЙ ФУНКЦИИ ARCCOS (_)






 mathematics
mathematics








