Аксиома параллельных прямых

1.

Урок 2
02.03.2019

2.

Геометрия
(планиметрия)
Понятия без
определений
(точка,
прямая)
логарифм
матрица
Признаки
Определения
Аксиомы
Теоремы
Свойства
Следствия
2

3.

Аксиома параллельных прямых.
Через точку, не лежащую на данной
прямой, проходит только одна прямая,
параллельная данной.
Следствия из аксиом (теорем)
Следствиями называются утверждения,
которые выводятся непосредственно из
аксиом или теорем.
3

4.

Следствия аксиомы параллельных
прямых :
1°. Если прямая пересекает одну из двух
параллельных прямых, то она пересекает и другую.
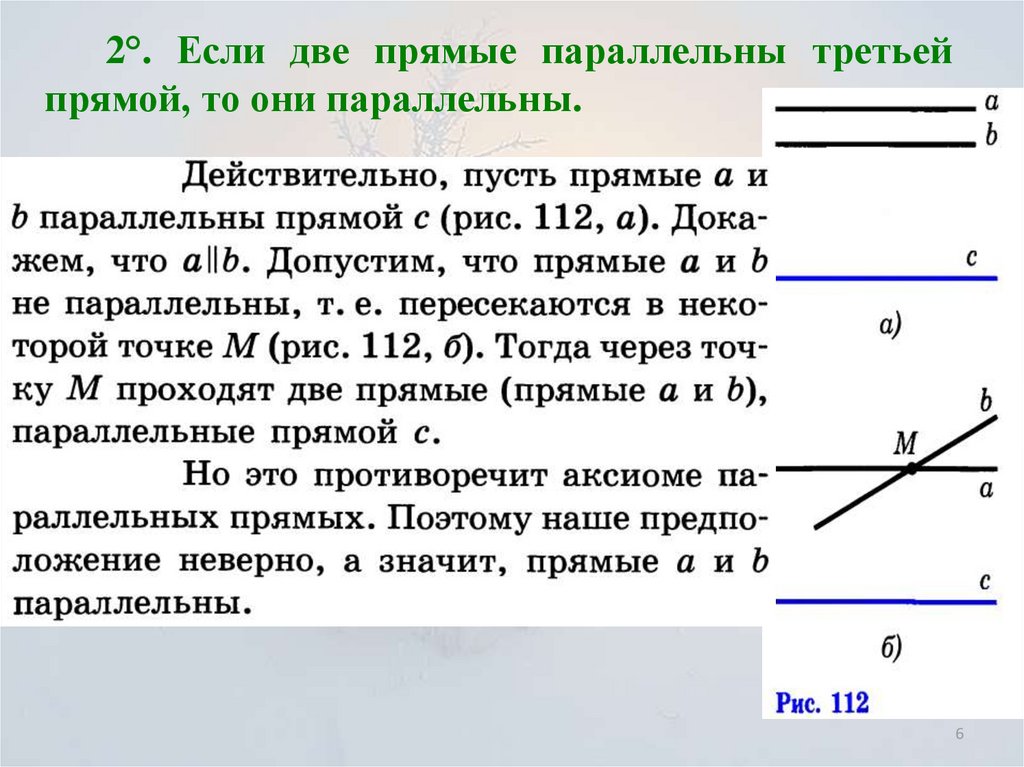
2°. Если две прямые параллельны третьей прямой,
то они параллельны.
4

5.

1°. Если прямая пересекает одну из двух
параллельных прямых, то она пересекает и другую.
5

6.

2°. Если две прямые параллельны третьей
прямой, то они параллельны.
6

7.

Упражнения
№ 198, 200, 208, 218, 219*
7

8.

Решение
№ 198
Прямые a и b перпендикулярны к прямой р, прямая с
пересекает прямую а. Пересекает ли прямая с прямую b?
Решение. По условию прямые а и b перпендикулярны к
прямой р, поэтому они не пересекаются (см. п. 12 учебника), т. е.
а || b. По условию прямая с пересекает одну из параллельных
прямых (прямую а), поэтому, согласно следствию 1° из аксиомы
параллельных прямых, она пересекает и прямую b.
Ответ. Да.
п. 12. Две прямые, перпендикулярные
к третьей, не пересекаются
8

9.

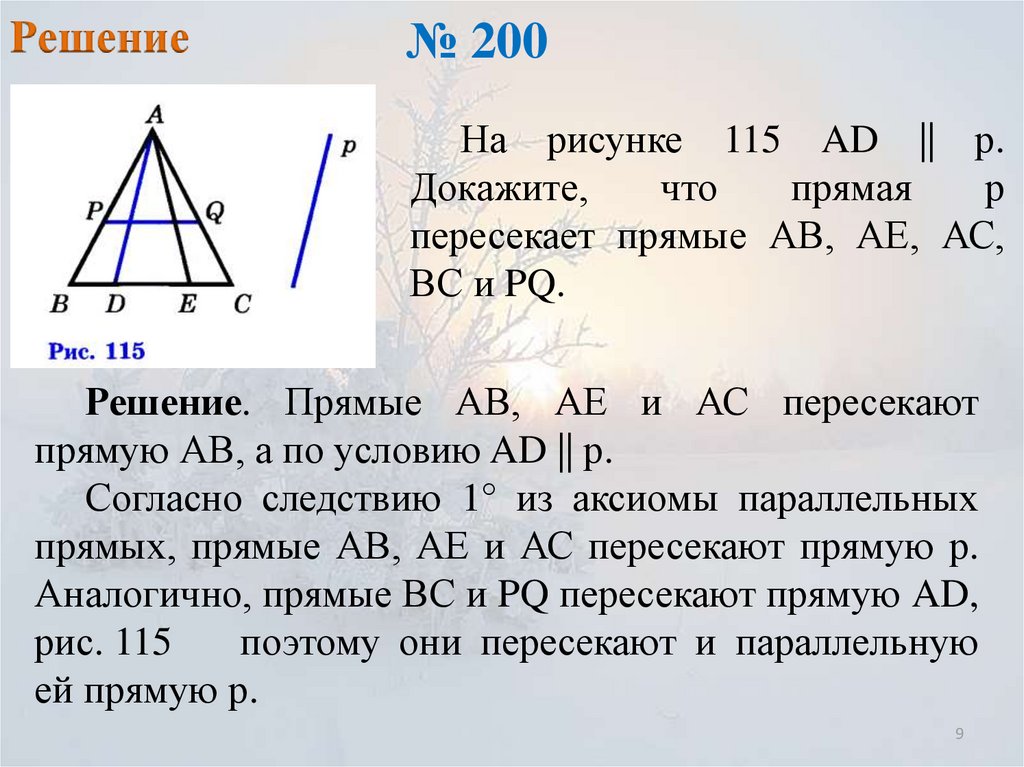
Решение
№ 200
На рисунке 115 AD || р.
Докажите,
что
прямая
р
пересекает прямые АВ, АЕ, АС,
ВС и PQ.
Решение. Прямые АВ, АЕ и АС пересекают
прямую АВ, а по условию AD || р.
Согласно следствию 1° из аксиомы параллельных
прямых, прямые АВ, АЕ и АС пересекают прямую р.
Аналогично, прямые ВС и PQ пересекают прямую AD,
рис. 115
поэтому они пересекают и параллельную
ей прямую р.
9

10.

№ 208
Решение
Разность
двух
односторонних
углов
при
пересечении двух параллельных прямых секущей равна
50°. Найдите эти углы.
Решение. Пусть < 1 и < 2 — односторонние углы
при пересечении параллельных прямых а и b секущей
с. Тогда < 1 + < 2 = 180°. По условию < 1 – < 2 = 50°,
следовательно, < 1 = 115°, < 2 = 65°.
Ответ. 115° и 65°.
2
1
10

11.

Решение
№ 218
Прямые а и b пересекаются.
Можно ли провести такую прямую,
которая пересекает прямую а и
параллельна прямой b? Ответ
обоснуйте.
Решение. На прямой а отметим точку М, не лежащую
на прямой b, и проведем через нее прямую с,
параллельную прямой b (рис. 138). Прямые а и с не
совпадают, так как прямая а пересекает прямую b, а с || b.
Таким образом, прямая с пересекает прямую а и
параллельна прямой b.
11
Ответ. Да.

12.

Решение
№ 219*
Даны две прямые а и b. Докажите, что если любая
прямая, пересекающая прямую а, пересекает и прямую
b, то прямые а и b параллельны.
Решение. Предположим, что прямые а и b не
параллельны, т. е. пересекаются.
Тогда можно провести такую прямую с, которая
пересекает прямую а и не пересекает прямую b (задача
218). Но это противоречит условию задачи. Значит,
наше предположение неверно, и а || b.
12

13.

Задание на с/п
Пункт 27, 28; ответить на вопросы 7–11
на с. 68 учебника; решить задачи № 213,
214, 215