Объем пирамиды

Цели :
• Научиться применять интегрирование функций в
качестве одного из способов решения задач на
нахождение объёмов геометрических тел.
• Развитие логического мышления, пространственного
воображения, умений действовать по алгоритму,
составлять алгоритмы действий.
• Воспитание познавательной активности,
самостоятельности.

4.

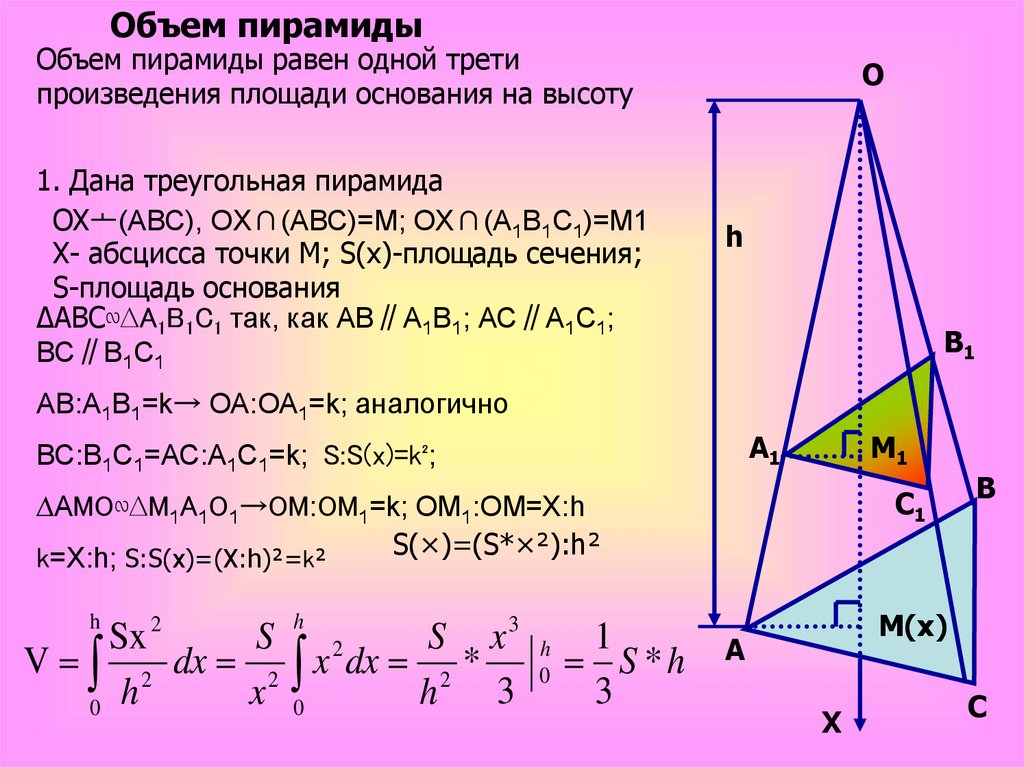
Объем пирамиды
Объем пирамиды равен одной трети
произведения площади основания на высоту
1. Дана треугольная пирамида
OXᅩ(АВС), OX∩(АВС)=М; OX∩(A1B1C1)=М1
Х- абсцисса точки М; S(x)-площадь сечения;
S-площадь основания
∆ABC∾∆A1B1C1 так, как АВ∥А1В1; АС∥А1С1;
ВС∥В1С1
O
h
B1
АВ:А1В1=k→ ОА:ОА1=k; аналогично
A1
ВС:В1С1=АС:А1С1=k; S:S(x)=k²;
M1
C1
∆AMO∾∆M1A1O1→OM:OM1=k; ОМ1:ОМ=Х:h
S(×)=(S*×²):h²
k=Х:h; S:S(x)=(Х:h)²=k²
h
h
3
Sx 2
S
S
x
V 2 dx 2 x 2 dx 2 *
3
x 0
h
0 h
h
0
1
S *h
3
B
M(х)
A
X
C

5.

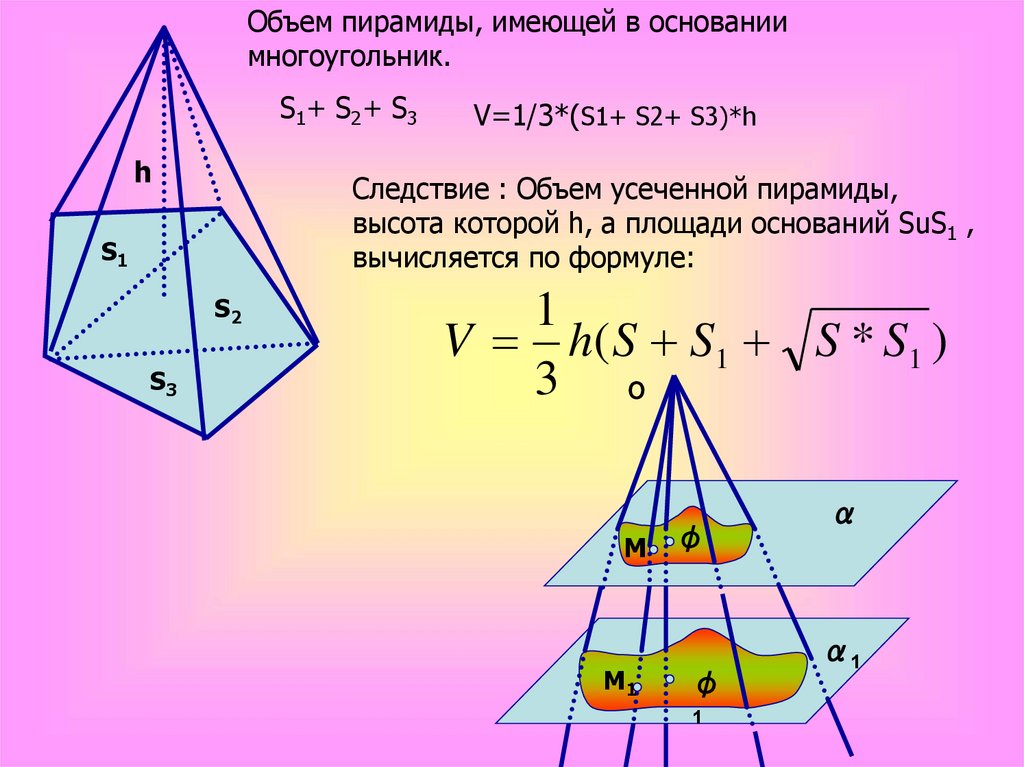
Объем пирамиды, имеющей в основании
многоугольник.
S1+ S2+ S3
h
Следствие : Объем усеченной пирамиды,
высота которой h, а площади оснований SuS1 ,
вычисляется по формуле:
S1
S2
S3
V=1/3*(S1+ S2+ S3)*h
1
V h( S S1 S * S1 )
3 O
М
М1
φ
φ
1
α
α1

6.

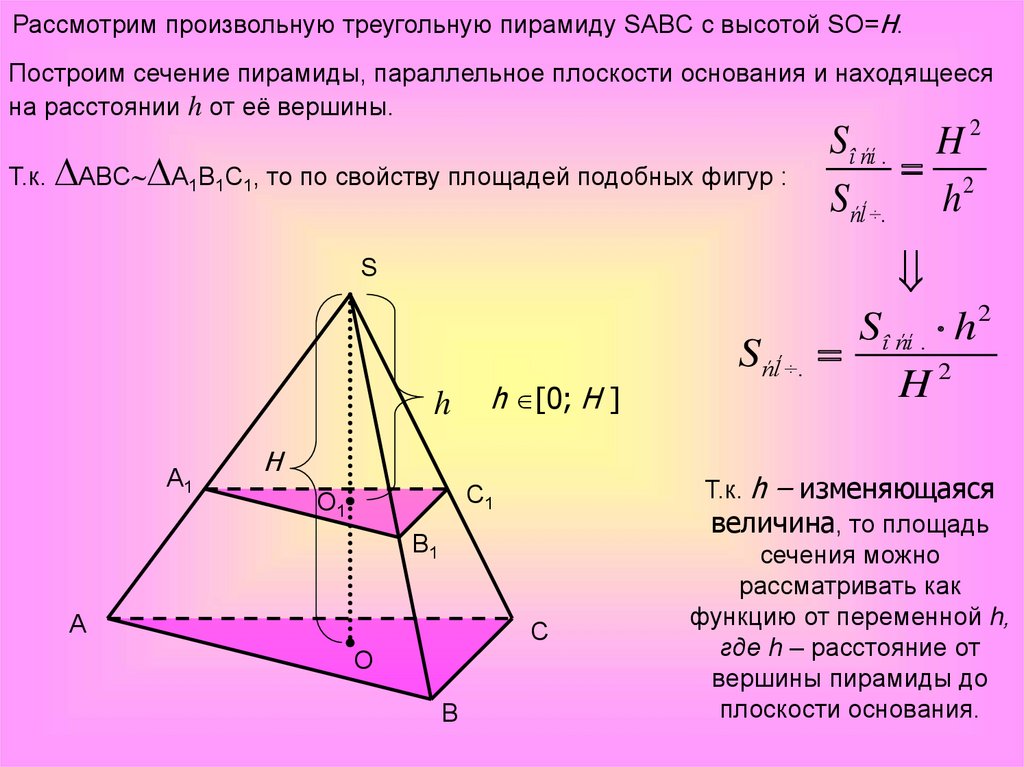
Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H.
Построим сечение пирамиды, параллельное плоскости основания и находящееся
на расстоянии h от её вершины.
Т.к. ABC A1B1C1, то по свойству площадей подобных фигур :
S
h
A1
Sî ńí . H 2
2
Sńĺ ÷. h
h [0; H ]
H
C1
O1
B1
A
C
O
B
Sńĺ ÷.
Sî ńí . h 2
H2
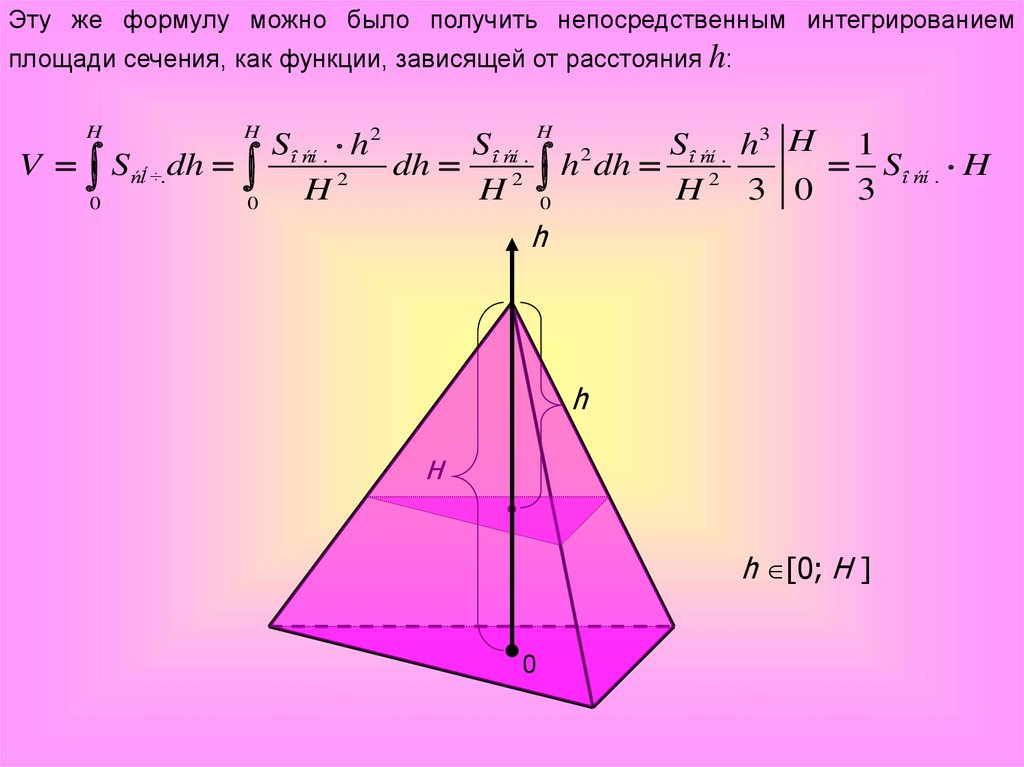
Т.к. h – изменяющаяся
величина, то площадь
сечения можно
рассматривать как
функцию от переменной h,
где h – расстояние от
вершины пирамиды до
плоскости основания.

7.

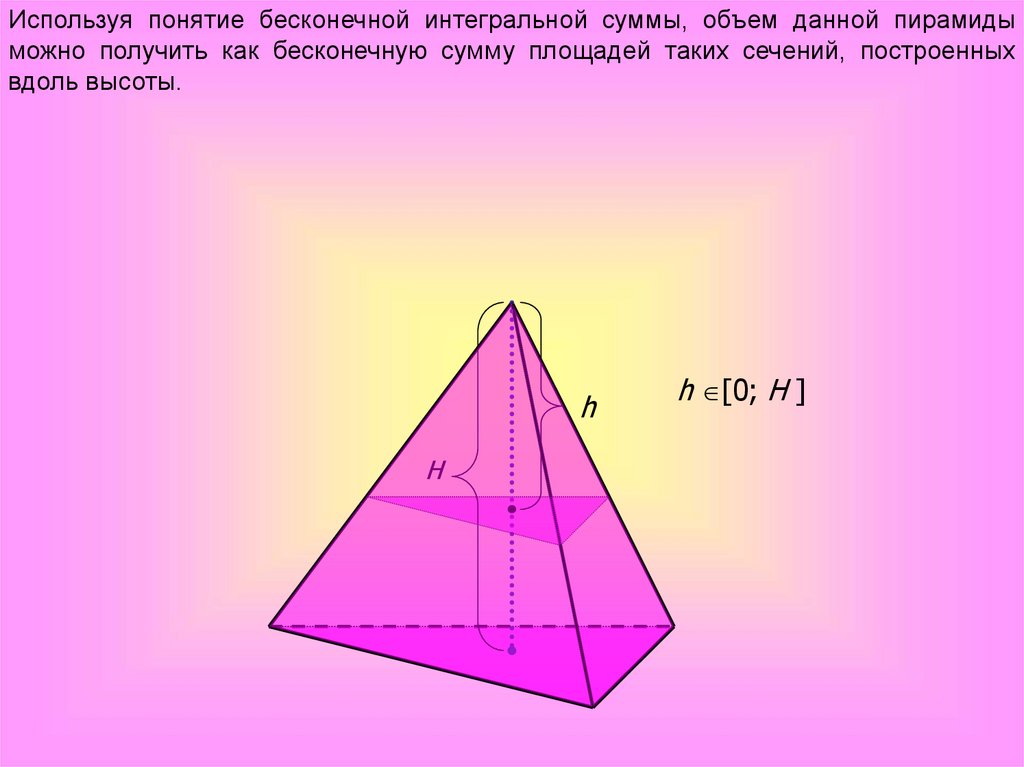
Используя понятие бесконечной интегральной суммы, объем данной пирамиды
можно получить как бесконечную сумму площадей таких сечений, построенных
вдоль высоты.
h
H
h [0; H ]

8.

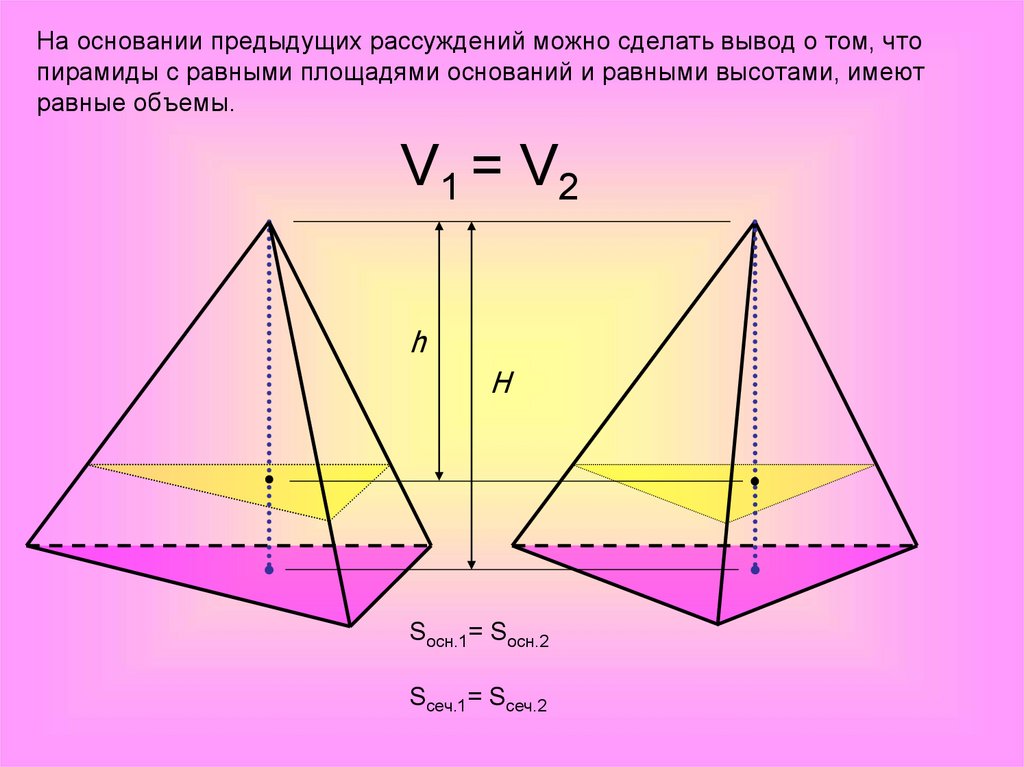
На основании предыдущих рассуждений можно сделать вывод о том, что
пирамиды с равными площадями оснований и равными высотами, имеют
равные объемы.
V1 = V2
h
H
Sосн.1= Sосн.2
Sсеч.1= Sсеч.2

9.

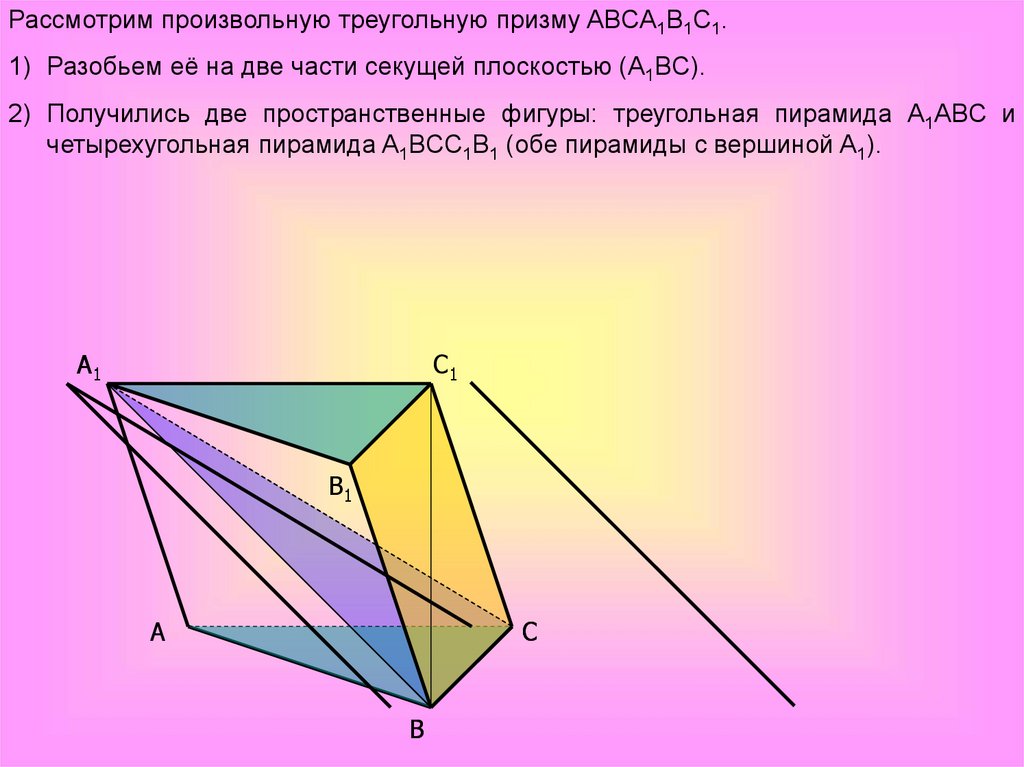
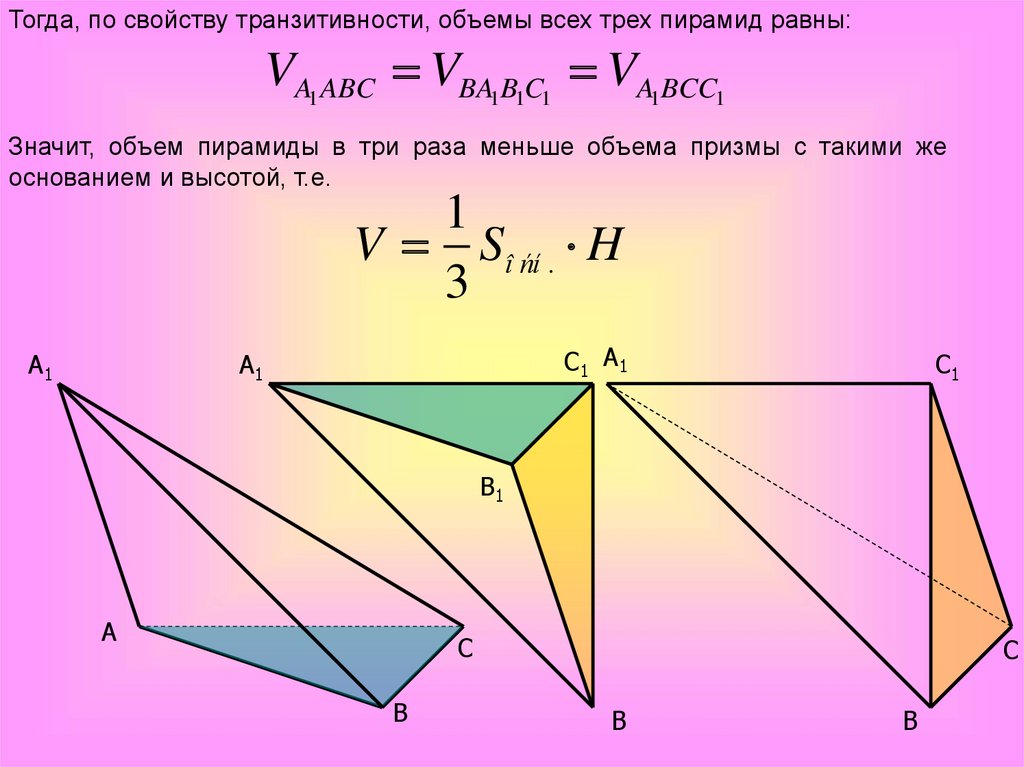
Рассмотрим произвольную треугольную призму ABCA1B1C1.
1) Разобьем её на две части секущей плоскостью (A1BC).
2) Получились две пространственные фигуры: треугольная пирамида A1ABC и
четырехугольная пирамида A1BCC1B1 (обе пирамиды с вершиной A1).
A1
C1
B1
A
C
B

10.

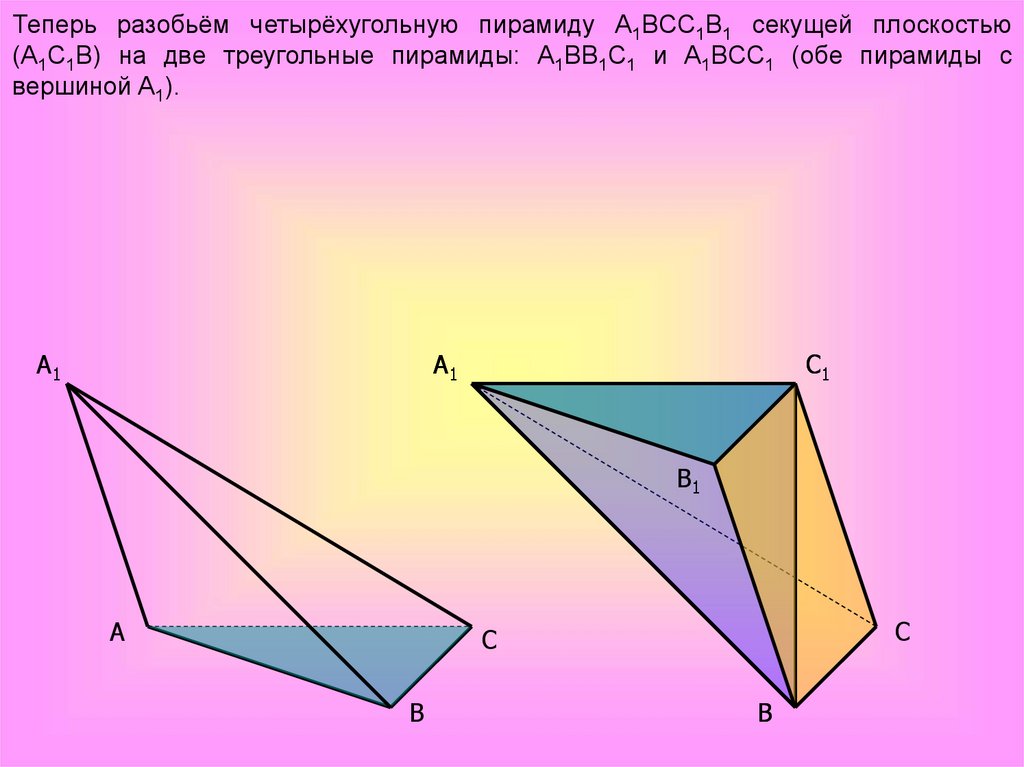
Теперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью
(A1C1B) на две треугольные пирамиды: A1BB1C1 и A1BCC1 (обе пирамиды с
вершиной A1).
A1
A1
C1
B1
A
C
C
B
B

11.

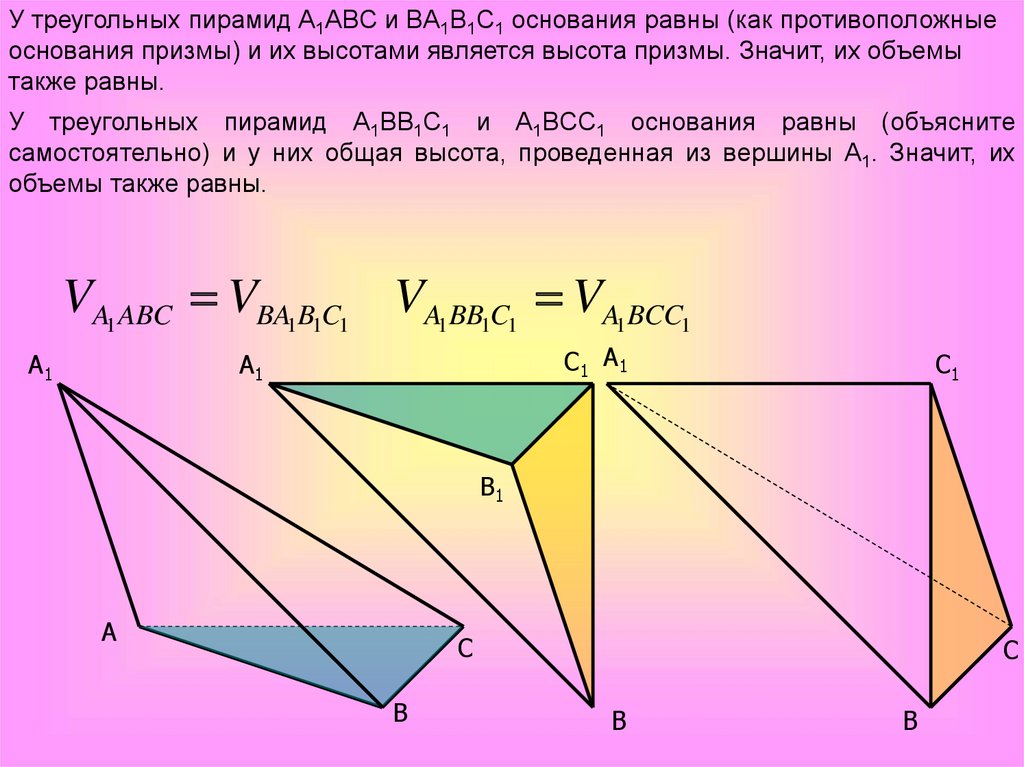
У треугольных пирамид A1ABC и BA1B1C1 основания равны (как противоположные
основания призмы) и их высотами является высота призмы. Значит, их объемы
также равны.
У треугольных пирамид A1BB1C1 и A1BCC1 основания равны (объясните
самостоятельно) и у них общая высота, проведенная из вершины A1. Значит, их
объемы также равны.
VA1 ABC VBA1B1C1 VA1BB1C1 VA1BCC1
A1
C1 A1
A1
C1
B1
A
C
B
C
B
B

12.

Тогда, по свойству транзитивности, объемы всех трех пирамид равны:
VA1 ABC VBA1B1C1 VA1BCC1
Значит, объем пирамиды в три раза меньше объема призмы с такими же
основанием и высотой, т.е.
1
V Sî ńí . H
3
A1
C1 A1
A1
C1
B1
A
C
B
C
B
B

13.

Эту же формулу можно было получить непосредственным интегрированием
площади сечения, как функции, зависящей от расстояния h:
H
V
S
0
H
ńĺ ÷.
dh
0
H
3
H 1
Sî ńí . h 2
Sî ńí .
S
h
2
î ńí .
dh
h dh
Sî ńí . H
2
2
2
H
H 0
H 3 0 3
h
h
H
h [0; H ]
0

14.

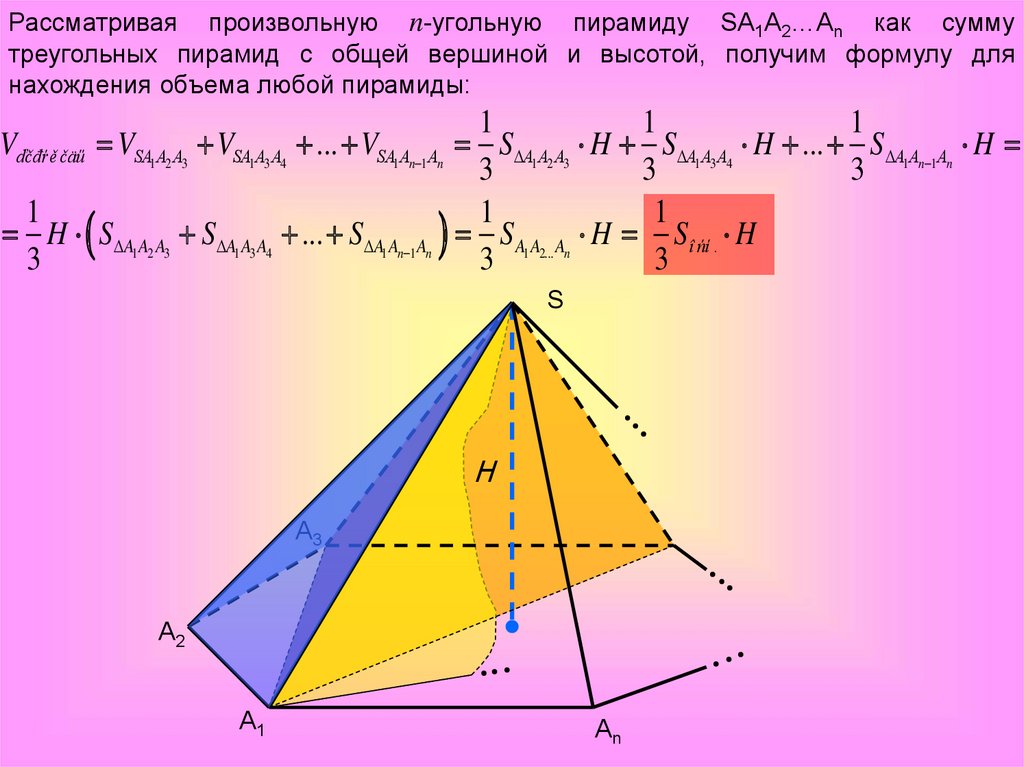
Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму
треугольных пирамид с общей вершиной и высотой, получим формулу для
нахождения объема любой пирамиды:
Vďčđŕě čäű VSA1 A2 A3 VSA1 A3 A4 ... VSA1 An 1 An
1
H S A1 A2 A3 S A1 A3 A4 ... S A1 An 1 An
3
1
1
1
S A1 A2 A3 H S A1 A3 A4 H ... S A1 An 1 An H
3
3
3
1
1
S A1 A2...An H Sî ńí . H
3
3
S
H
A3
A2
A1
An

15.

Итак, для любой n-угольной пирамиды:
Vďčđŕ ě čäű
1
Sî ńí . H
3
,где Sосн. – площадь основания пирамиды, H – высота пирамиды.

16.

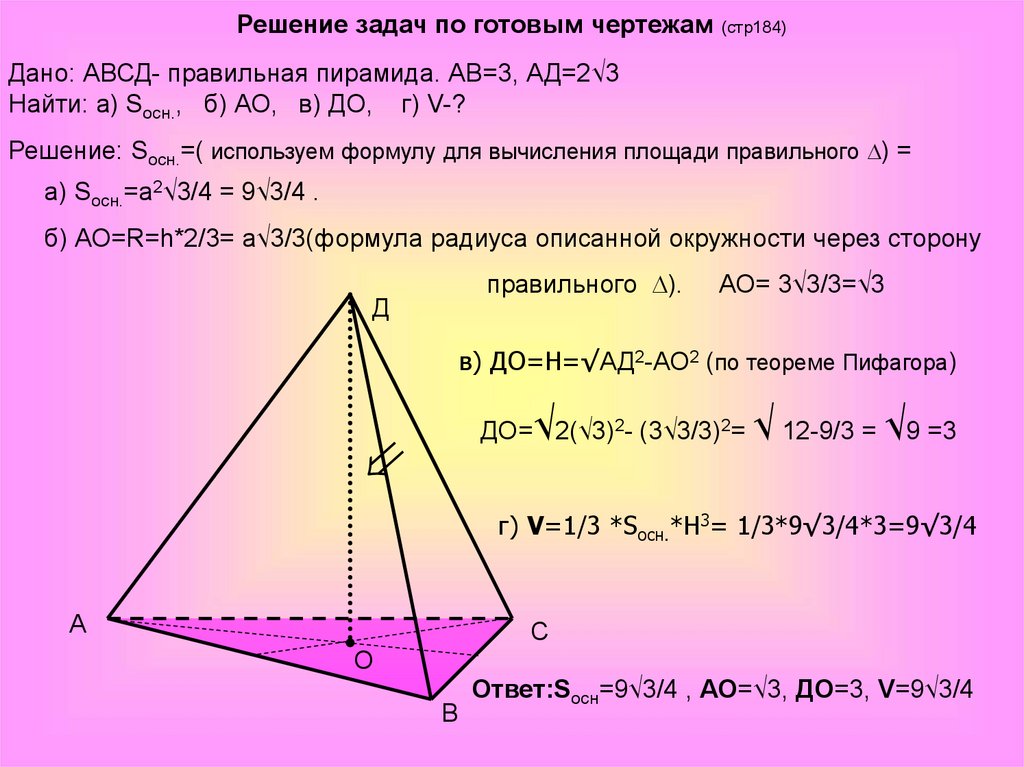
Решение задач по готовым чертежам
(стр184)
Дано: АВСД- правильная пирамида. АВ=3, АД=2√3
Найти: а) Sосн., б) АО, в) ДО, г) V-?
Решение: Sосн.=( используем формулу для вычисления площади правильного ) =
а) Sосн.=а2√3/4 = 9√3/4 .
б) АО=R=h*2/3= а√3/3(формула радиуса описанной окружности через сторону
правильного ).
Д
АО= 3√3/3=√3
в) ДО=H=√АД2-АО2 (по теореме Пифагора)
ДО=√2(√3)2- (3√3/3)2= √ 12-9/3 = √9 =3
г) V=1/3 *Sосн.*Н3= 1/3*9√3/4*3=9√3/4
A
C
O
B
Ответ:Sосн=9√3/4 , АО=√3, ДО=3, V=9√3/4

17.

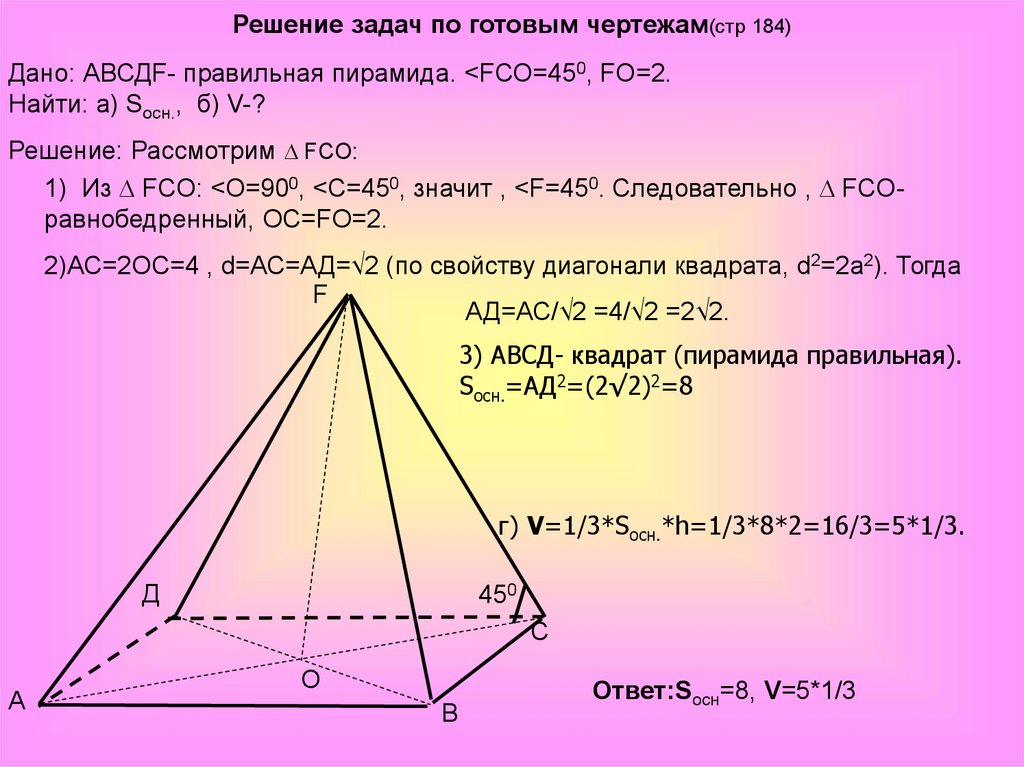
Решение задач по готовым чертежам(стр 184)
Дано: АВСДF- правильная пирамида. <FСО=450, FО=2.
Найти: а) Sосн., б) V-?
Решение: Рассмотрим FCO:
1) Из FCO: <O=900, <С=450, значит , <F=450. Следовательно , FCOравнобедренный, ОС=FО=2.
2)АС=2ОС=4 , d=АС=АД=√2 (по свойству диагонали квадрата, d2=2а2). Тогда
F
АД=АС/√2 =4/√2 =2√2.
3) АВСД- квадрат (пирамида правильная).
Sосн.=АД2=(2√2)2=8
г) V=1/3*Sосн.*h=1/3*8*2=16/3=5*1/3.
Д
450
C
A
O
B
Ответ:Sосн=8, V=5*1/3

18.

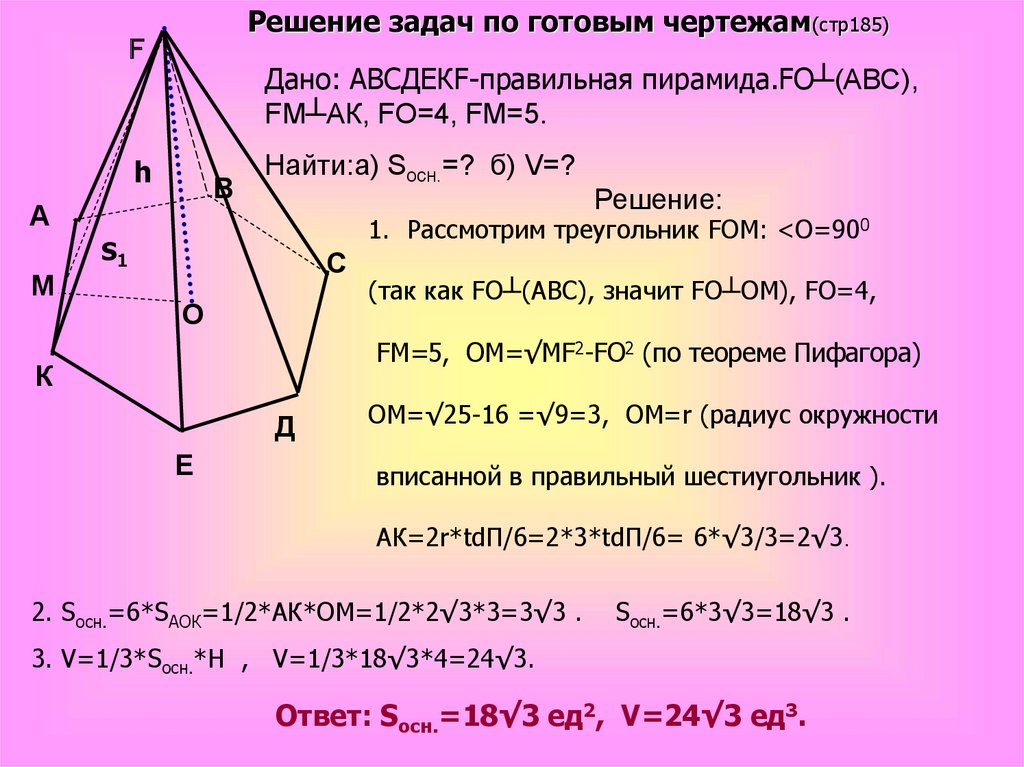
Решение задач по готовым чертежам(стр185)
F
Дано: АВСДЕКF-правильная пирамида.FО┴(АВС),
FМ┴АК, FO=4, FМ=5.
h
В
А
М
Найти:а) Sосн.=? б) V=?
Решение:
1. Рассмотрим треугольник FОМ: <О=900
S1
С
О
(так как FО┴(АВС), значит FО┴ОМ), FO=4,
FМ=5, ОМ=√МF2-FO2 (по теореме Пифагора)
К
Д
Е
ОМ=√25-16 =√9=3, ОМ=r (радиус окружности
вписанной в правильный шестиугольник ).
АК=2r*tdП/6=2*3*tdП/6= 6*√3/3=2√3.
2. Sосн.=6*SАОК=1/2*АК*ОМ=1/2*2√3*3=3√3 .
Sосн.=6*3√3=18√3 .
3. V=1/3*Sосн.*H , V=1/3*18√3*4=24√3.
Ответ: Sосн.=18√3 ед2, V=24√3 ед3.

19.

Свойство объемов №1
Равные тела имеют равные объемы
Свойство объемов №2
Если тело составлено из нескольких тел, то
его объем равен сумме объемов этих тел.
Свойство объемов №3
Если одно тело содержит другое, то объем
первого тела не меньше объема второго.

20.

Домашнее задание
П. 69, № 684а, 686а, 687.

21.

Библиография
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев
«Геометрия, 10-11», М., Просвещение, 2007
В.Я. Яровенко «Поурочные разработки по
геометрии», Москва, «ВАКО», 2006

English Русский Rules