Similar presentations:
Прискорювач чи енерджайзер, взаємозв’язок iмпульсу, маси та енергiї в СТВ
1.
Accelarator or Energyzer?Prof. Oleksandr
Slobodyanyuk
Department of Physics
Taras Shevchenko University of Kyiv,
Ukraine
2. Київський національний університет імені Тараса Шевченка фізичний факультет
Прискорювач чи енерджайзер?(взаємозв’язок iмпульсу, маси та енергiї в СТВ)
Проф. О. В. Слободянюк
slobod@univ.kiev.ua
21.02.2019
© О. Слободянюк, 2012
2
3.
Ми повинні бути вдячними Богу за те,що він створив світ так,
що все просте –правда, а все
складне – неправда.
Григорiй Сковорода
Gott würfelt nicht
Albert Einstein
God doesn't play dice
with the world
Albert Einstein
4. Декілька простих питань:
• Що робить прискорювач зарядженихчастинок?
• Прискорює частинки.
• Що означає – прискорює?
• Збільшує їх швидкість.
• Чи це дійсно так?
• Не зовсім….
• Чому?
21.02.2019
© О. Слободянюк, 2007
4
5. Декілька простих питань:
21.02.2019
Що повинен робити енерджайзер?
Збільшувати енергію частинок.
Чи збільшується при цьому їх швидкість?
Так.
Чи літають крокодили?
Так. Літають.
Але дуже, дуже низенько..
© О. Слободянюк, 2007
5
6. Чи коректно записана формула?
UUSS Enterprise7. Яку з формул обрати?
E=mc2E0=mc2
E=m0c2
E0=m0c2
8. Яку з формул обрати?
21.E=mc
2
2.E0=mc
2
3.E=m0c
2
4.E0=m0c
9. Постулати Ньютона та постулати Айнштайна
• Ньютон:1. існування інерціальних систем відліку (ІСВ);
2. принцип відносності механіки;
3. принцип далекодії - взаємодії поширюється
миттєво).
• Айнштайн:
0. існування інерціальних систем відліку (ІСВ);
1. принцип відносності електродинаміки;
2. принцип близькодії - швидкість поширення
взаємодії скінченна і дорівнює швидкості
поширення світла.
10. Постулати Ньютона та постулати Айнштайна
• Існування інерціальних систем відліку (ІСВ)• Ньютон: принцип відносності механіки
Айнштайн: + принцип відносності
електродинаміки
• Ньютон: принцип далекодії
Айнштайн: принцип близькодії (швидкість
поширення взаємодії скінченна і дорівнює
швидкості поширення світла)
11.
СТВ: Перетворення Лоренцаx'
x
K'
x'
K
x
K'
x
x'
K
K'
K
.
O'
z'
O
z
z'
O'
O'
z
O
z'
z
O
y'
y'
y
y'
y
y
( x )2 ( y )2 ( z )2 (c )2 (t )2
x y z c t
2
x x ,
2
2
2 2
y y ,
z =
z Vt
2
V
1 2
c
V
t 2 z
c
t =
2
V
1 2
c
12.
Перетворення Лоренца і Галілея1
0
L 0
0
0
0
1
0
1
0
0
1 2
i
1 2
0
i
1 2
1
2
1
0
1
0
G
0
0
0 0 0
1 0 0
0 1 V
0 0 1
Інтервал
S122 c 2 t122 l122
S12 c t2 t1 x2 x1 y2 y1 z2 - z1
2
2
2
2
2
13.
Наслідки перетворень ЛоренцаСкорочення просторових інтервалів
l l0 1 2
Уповільнення часу
0
1 2
S122 c 2 t122 l122
14.
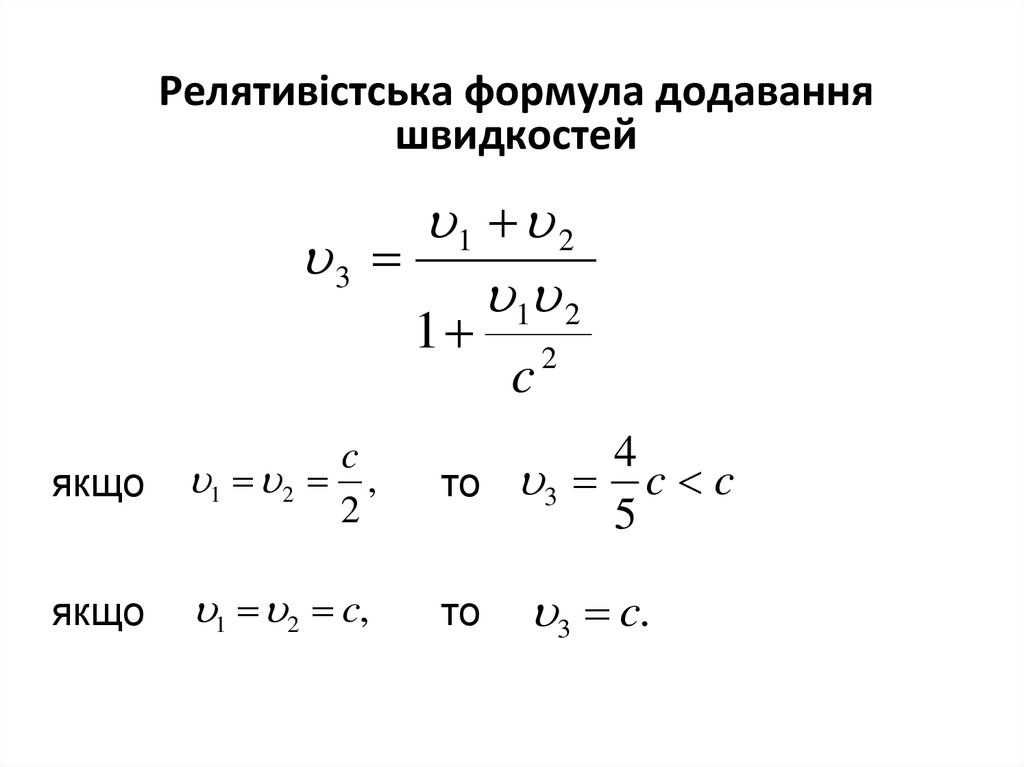
Релятивістська формула додаванняшвидкостей
1 2
3
1 2
1
c
2
якщо
c
1 2 ,
2
4
то 3 c c
5
якщо
1 2 c,
то
3 c.
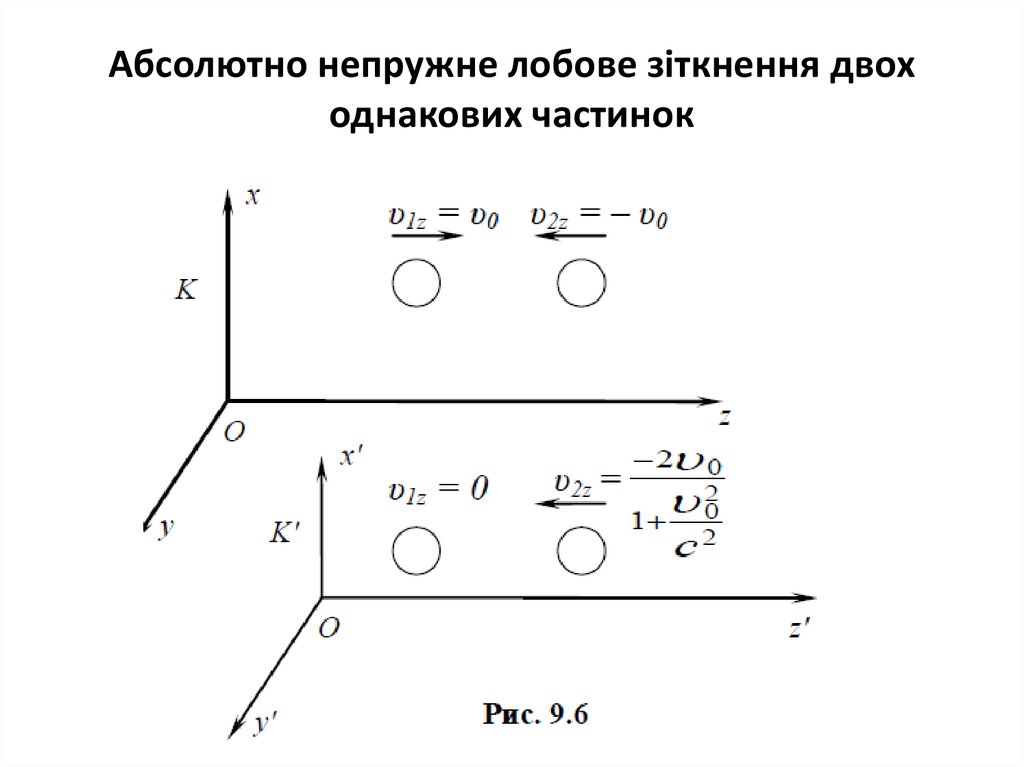
15. Абсолютно непружне лобове зіткнення двох однакових частинок
16. Абсолютно непружне лобове зіткнення двох однакових частинок
KАбсолютно непружне лобове зіткнення двох
однакових частинок
Закон збереження імпульсу в системі відліку K:
p1z p2 z ~
p1z ~
p2 z
~
~
~
Pz p1z p2 z m( 0 0 ) 0 p1z p2 z Pz
2m ~z 0 звідки ~z 0
Закон збереження імпульсу в системі відліку K’ дає:
~
Pz 2mυ~z 2mυ0
звідки
υ~z υ0
17. Абсолютно непружне лобове зіткнення двох однакових частинок
Швидкості частинок у системі відліку K’ до і після зіткнення можнатакож знайти, застосувавши релятивістську формулу перетворення
швидкостей, а потім знову використати ньютонівський вираз для
знаходження імпульсів частинок у системі відліку K’:
Сумарний імпульс до зіткнення:
Pz p1 z p2 z m 1 z m 2 z
2m 0
1
а після зіткнення:
~
Pz 2m ~ z 2m 0 .
c
2
0
2
18.
Висновок:Для імпульсів системи двох частинок знайдених у такий
спосіб, а саме, із застосуванням релятивістського
закону додавання швидкостей та ньютонівської
формули для імпульсу частинки, закон збереження
імпульсу не виконується:
2m 0
1
c
2
0
2
2m 0 !
19.
Релятивістський вираз для імпульсу.
Імпульс частинки у вигляді
p
mυ
υ
1 2
c
2
буде інваріантним відносно перетворень Лоренца і
законом збереження імпульсу у його звичній формі можна
буде користуватися при будь-яких швидкостях
c
20.
Взаємозв’язок iмпульсу, маси та енергiї в СТВВиявляється, що так само як просторовий відрізок і
проміжок часу між двома подіями кожен окремо не
залишаються незмінними при переході від однієї ІСВ до
іншої, величини імпульсу і енергії частинки також не
залишаються незмінними кожна окремо при переході від
однієї ІСВ до іншої.
Натомість вони пов’язані співвідношенням:
E p c m c
υE
p 2
де
c
2
2 2
2 4
21.
Взаємозв’язок iмпульсу, маси та енергiї в СТВПри переході від ІСВ до ІСВ компоненти вектора
імпульсу частинки та енергія частинки перетворюються
за формулами перетворень Лоренца:
p x px ,
p y p y ,
V
pz 2 E
c
p z =
V2
1 2
c
E =
E Vp z
V2
1 2
c
22.
Взаємозв’язок iмпульсу, маси та енергiї в СТВ.
Аналогічно до того, як записують довжину 4-вектора
( x, y, z , ct ) у вигляді
S122 c 2t122 l122
E
,довжину 4-вектора ( p , p , p ,
)
x
y
z
c
можна записати як
2
E
2
2 2
p m c
2
c
E2
2
p
c2
23.
Взаємозв’язок iмпульсу, маси та енергiї в СТВІз основних співвідношень:
E p c m c
2
2 2
2 4
υE
p 2
c
та
для безмасових частинок, m=0
E
p ,
c
а для масивних частинок, m≠0
p=
m
1
2
та
E
mc2
1 2
.
24.
Взаємозв’язок iмпульсу, маси та енергiї в СТВПри v=0
E0 mc
mc
Eк E E0
Eк mc2 [(1 2 )
2
1
При малих швидкостях
1
2
2
2
mc2 mc2 [(1 2 )
c
1
2
1]
1
2
2
1
m
1] mc2 [(1 2 1] mc2 2
2
2c
2
25.
26.
ВисновокХоча велетенські машини, розміри яких сягають декількох
кілометрів, а для своєї роботи вони потребують
потужності, яку в середньому споживає велике місто, за
звичкою продовжують називати прискорювачами, їх
основною задачею є не надання ще більшої швидкості
зарядженим частинкам, яка переважно відрізняється від
швидкості світла менше, ніж на 10-8 %, а надання
частинкам якомога більшої енергії.
27. Декілька простих питань:
1. Чи літають крокодили?• Так. Літають.
• Але дуже, дуже низенько..
2. Чи прискорює прискорювач частинки?
• Так. Прискорює.
• Але дуже, дуже слабенько..
21.02.2019
© О. Слободянюк, 2007
27
28. Декілька простих питань:
21.02.2019
Що повинен робити енерджайзер?
Збільшувати енергію частинок.
Чи збільшується при цьому їх швидкість?
Так.
Чи літають крокодили?
Так. Літають.
Але дуже, дуже низенько..
© О. Слободянюк, 2007
28
29.
Прискорювач чи енерджайзер?Має місце введення в оману платників податків….
Хіба це прискорення?
За кожен додатковий см/с треба заплатити 1 M$...
Назву треба привести назву у відповідність із суттю
справи…
На рекламному “новоязі”: мерчандайзер, освіжайзер…
Отже
Енерджайзер!
30.
Thank your for you kind attention!31.
Імпульс, маса та енергiя системи частинок.Дефект маси. Приклади.
Див. с. 435-439 у доданому файлі
Слободянюк_Механіка_9_for Problems XX.doc
32.
Приклади перетворення енергії спокою накінетичну енергію і навпаки: анігіляція
частинок і античастинок, народження
частинок, реакції ділення та синтезу ядер,
хімічні реакції.
Див. с. 439-442 у доданому файлі
Слободянюк_Механіка_9_for Problems XX.doc
33.
Імпульс, маса та енергiя системи частинок.Дефект маси. Приклади.
,
34.
Ефект КомптонаLight–matter interaction
Low-energy phenomena:
Photoelectric effect
Mid-energy phenomena:
Thomson scattering
Compton scattering
High-energy phenomena:
Pair production
35.
Ефект КомптонаLight–matter interaction
Thomson scattering is the elastic scattering of
electromagnetic radiation by a free charged particle, as
described by classical electromagnetism.
It is just the low-energy limit of Compton scattering: the
particle kinetic energy and photon frequency are the same
before and after the scattering.
36.
Ефект КомптонаFrom Wikipedia, the free encyclopedia:
• Комптонівське розсіювання — явище непружного
розсіювання фотонів на вільних заряджених частинках,
наприклад, електронах (українська).
• Эффе́кт Ко́ мптона - некогерентное рассеяние фотонов
на свободных электронах (русский).
• Compton scattering is the inelastic scattering of
a photon by a charged particle, usually an electron. It results in
a decrease in energy (increase inwavelength) of the photon
(which may be an X ray or gamma ray photon), called
the Compton effect.
37.
Ефект КомптонаФизическая энциклопедия, т.2, стр.431:
38.
Ефект Комптона:Пружне чи непружне розсіяння? Де правда?
Правда тут:
39.
Ефект Комптона - це пружне розсіянняДив. доданий файл
Compton_scattering_2016_0114







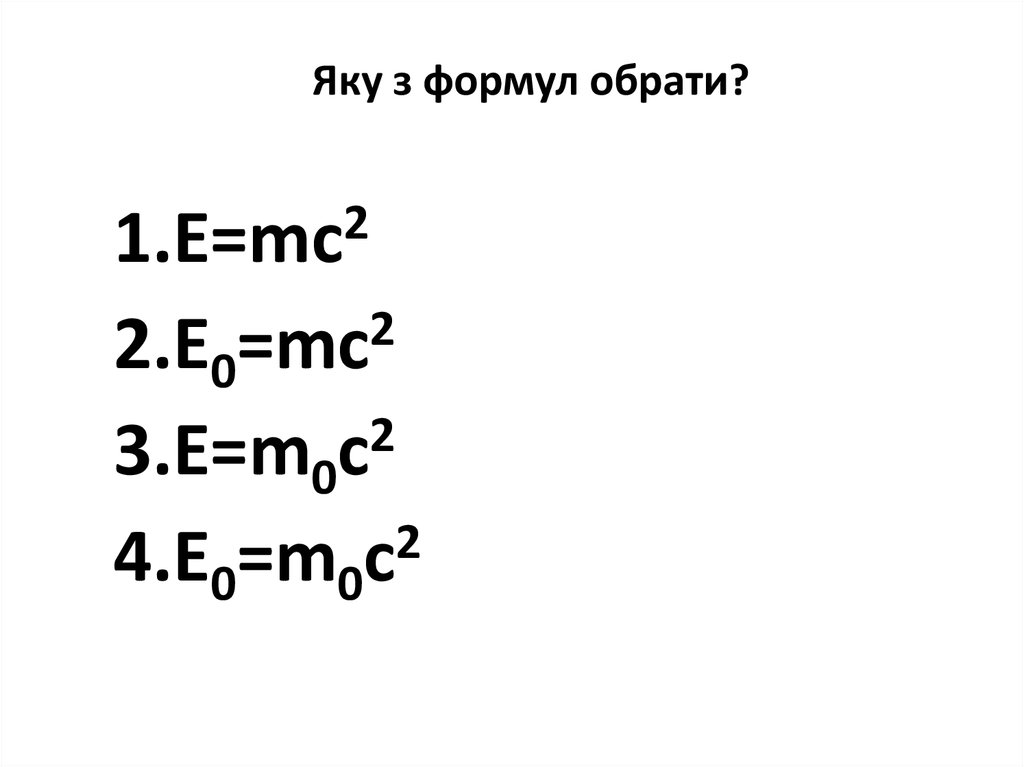




























 physics
physics








