Вариация альтернативного признака. Лекция 9. Дисперсии

1. Вариация альтернативного признака.

.
В ряде случаев возникает необходимость в
измерении дисперсии альтернативных признаков,
т.е. признаков, которыми одни единицы обладают
и не обладают другие.
Обозначим наличие данного признака 1,
отсутствие 0, долю вариантов, обладающих
данным признаком р, а не обладающих им q.
06:05
1

2.

Так как р + q = 1 (q = 1- p), то средняя
1 p 0 q
x
p
p q
а дисперсия альтернативного признака
2
2
(
1
p
)
p
(
0
p
)
q 2
2
q p p 2 q pq (q p) pq
p q
Таким образом, дисперсия альтернативного признака равна
произведению доли единиц, обладающих данным свойством
(p), на долю единиц, данным свойством не обладающих (q).
06:05
m n — число наблюдений,
p
m — число единиц совокупности,
n
обладающих данным признаком
2

3.

Пример.
Определим дисперсию альтернативного признака по
следующим данным: налоговой инспекцией одного из
районов города проверено 200 коммерческих киосков и в
150 обнаружены финансовые нарушения.
Тогда
n = 200, m = 150;
р =150/200=0,75;
q = 1 - 0,75 = 0,25;
2
= 0,75*0,25 = 0,1875.
06:05
3

4.

Наряду с изучением вариации признака по всей
совокупности в целом часто бывает необходимо
проследить количественные изменения признака по
группам, на которые разделяется совокупность, а также
между группами. Такое изучение вариации достигается
посредством вычисления и анализа различных видов
дисперсии.
Правило сложения дисперсий.
Если данные представлены в виде
аналитической группировки, то можно вычислить
дисперсию общую,
межгрупповую
и внутригрупповую.
06:05
4

5.

Общая дисперсия измеряет вариацию признака
во всей совокупности под влиянием всех
факторов, обусловливающих эту вариацию:
n
2
xi x f i
2
i 1
n
fi
i 1
06:05
5

6.

Межгрупповая дисперсия характеризует
систематическую вариацию, т.е. различия в
величине изучаемого признака, возникающие под
влиянием признака-фактора, положенного в
основание группировки. Она рассчитывается по
m
формуле
2
2
xi x f i
i 1
m
fi
i 1
xi - средняя i-й группы
x - общая средняя варьирующего признака х;
fi
- частота i-й группы.
06:05
6

7.

Внутригрупповая
дисперсия
отражает
случайную
вариацию,
т.е.
часть
вариации,
происходящую под влиянием неучтенных факторов, и
не зависящую от признака-фактора, положенного в
основание
группировки.
Данная
дисперсия
рассчитывается отдельно для каждой i-й группы:
fk
2
k
xi xk
2
i 1
fk
xi - значение признака у отдельных элементов совокупности;
f k - число единиц в группе k.
06:05
7

8.

Для всех групп в целом вычисляется
средняя
из
внутригрупповых
дисперсий,
взвешенных на частоты соответствующих групп
по формуле
m
2
f k
k 1
m
2
k
fk
k 1
06:05
8

9.

Взаимосвязь между тремя дисперсиями
получила название правила сложения дисперсий,
в соответствии с которым:
2
2
2
- общая дисперсия
2
2
2
- межгрупповая дисперсия
- средняя из внутригрупповых дисперсий
т. е. согласно этому правилу общая дисперсия,
возникающая под влиянием всех факторов, равна
сумме дисперсии, возникающей за счет
группировочного признака, и дисперсий, возникающих
под влиянием всех прочих факторов.
Зная любые два вида дисперсий, можно определить
06:05
или
проверить правильность расчета третьего вида. 9

10.

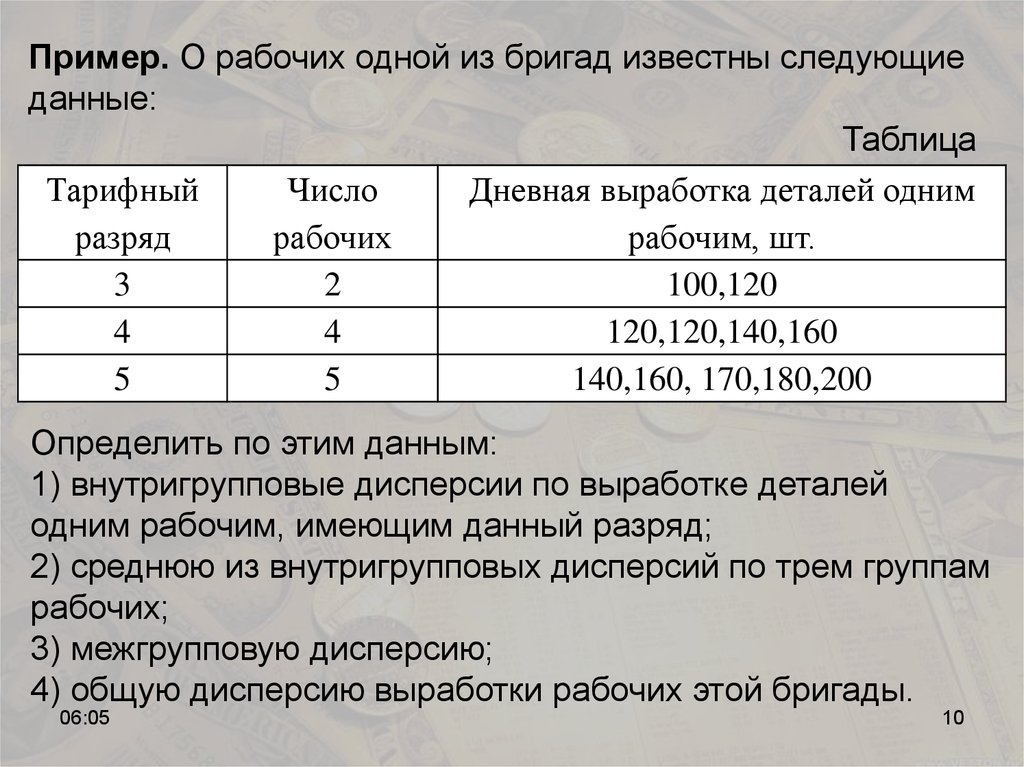
Пример. О рабочих одной из бригад известны следующие
данные:
Таблица
Тарифный
Число
Дневная выработка деталей одним
разряд
рабочих
рабочим, шт.
3
2
100,120
4
4
120,120,140,160
5
5
140,160, 170,180,200
Определить по этим данным:
1) внутригрупповые дисперсии по выработке деталей
одним рабочим, имеющим данный разряд;
2) среднюю из внутригрупповых дисперсий по трем группам
рабочих;
3) межгрупповую дисперсию;
4) общую дисперсию выработки рабочих этой бригады.
06:05
10

11.

Решение. 1) Для расчета внутригрупповых дисперсий
вычислим средние по каждой группе:
100 120
x1
110
2
.
120 120 140 160
x2
135
4
140 160 170 180 200
x3
170
5
06:05
11

12.

Рассчитаем внутригрупповые дисперсии по выработке
деталей одним рабочим, имеющим данный разряд:
f1
2
1
хi x1
2
i 1
f1
f2
2
2
f2
f3
2
3
xi x 3
i 1
f3
06:05
2
х
x
2
2
i 1
100
110
120
110
i 1
2
xi x 2
i 1
2
2
2
2
2
2
2
120 135 120 135 140 135 160 135
4
2
200
100
2
2
2
2
2
2
140 170 160 170 170 170 180 170 200 170
5
1100
275
4
2000
400
5
12

13.

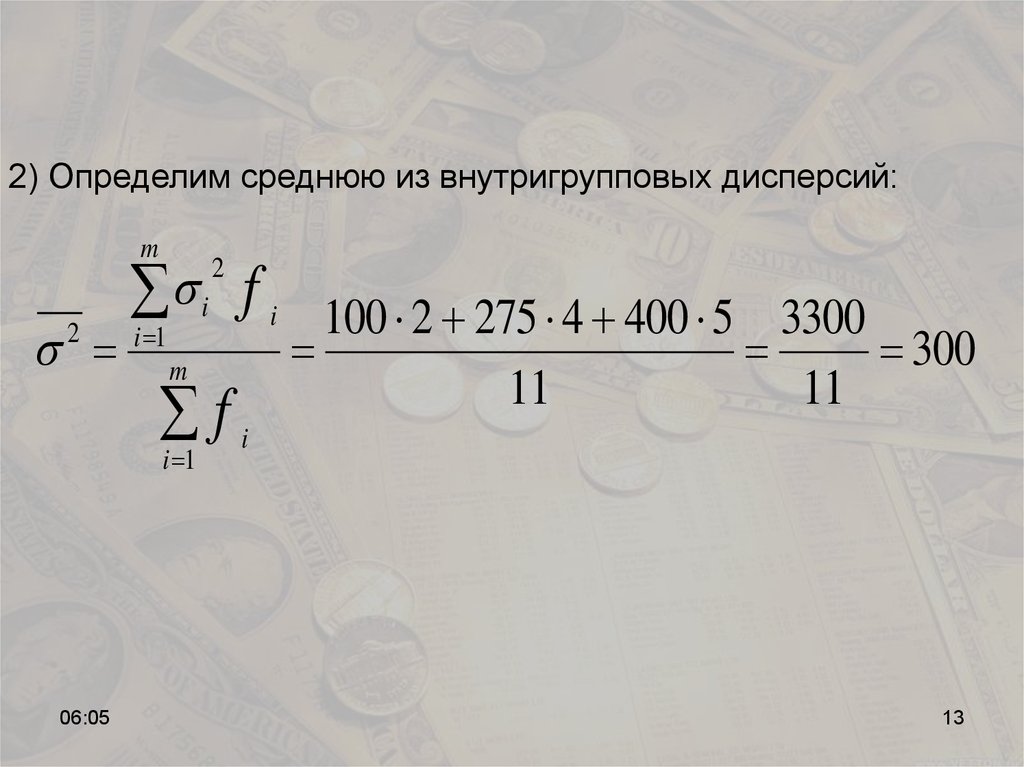
2) Определим среднюю из внутригрупповых дисперсий:
m
2
i f i
2
i 1
m
fi
100 2 275 4 400 5 3300
300
11
11
i 1
06:05
13

14.

3) Определим общую среднюю величину для расчета
межгрупповой дисперсии.
m
xоб
xi fi
1
m
110 2 135 4 170 5 1610
146,4
11
11
fi
1
Теперь определим межгрупповую дисперсию:
m
2
2
x
x
fi
i
1
m
fi
1
110 146,4 2 2 135 146,4 2 4 170 146,4 2 5 5954,56 541,3
11
06:05
11
14

15.

4) Определим общую дисперсию обычным способом:
n
2
2
xi x
i 1
n
2
2
2
110 146,4 120 146,4 ... 200 146,4 9254,56
841,3
11
11
Проверим полученный результат, вычислив общую
дисперсию по правилу сложения дисперсий:
2
2 541,3 300 841,3
2
Таким образом, общая дисперсия, вычисленная по правилу
сложения дисперсий, в точности совпадает по числовому
значению с результатом вычисления ее непосредственно на
основе
данных по всей совокупности рабочих.
06:05
15

16.

На основании правила сложения дисперсий можно
определить показатель тесноты связи между
группировочным (факторным) и результативным признаками.
Он называется эмпирическим корреляционным
отношением, обозначается («эта») и рассчитывается по
2
формуле
x
2
Эмпирический коэффициент детерминации представляет
собой долю межгрупповой дисперсии в общей дисперсии
2
2
x
2
Для нашего примера эмпирическое корреляционное
отношение:
541,3
0,64 0,8
06:05
841,3
16

17.

Этот показатель (η) принимает значения в интервале [0, 1]:
чем ближе к 1, тем теснее связь, и наоборот.
Можно руководствоваться рекомендациями по оценке
тесноты связи:
если
η < 0,3 — связь слабая;
0,3 < η < 0,5 — связь заметная;
0,5 < η < 0,7 — связь умеренно тесная;
η > 0,7 — связь тесная.
Для нашего примера можно сделать вывод о том, что
между дневной выработкой деталей и квалификацией
рабочих существует тесная статистическая связь, так как
корреляционное отношение равно 0,8.
06:05
17

18.

Для проверки существенности связи между
группировочным признаком и вариацией
исследуемого признака часто используется
дисперсионное отношение F (критерий Фишера).
2 2
F
1 2
где 1, и 2 - число степеней свободы для
сравниваемых дисперсий,
при этом 1= m-1; 2= N-m;
N - число наблюдений.
m - число групп,
для рассмотренного примера 1=3-1=2;
2=11-3=8
06:05
18

19.

Расчетное значения критерия Фишера (Fрасч)
сравнивается с критическим (Fкр ), которое
определяется по таблицам в зависимости от числа
степеней свободы и уровня значимости.
Если Fрасч >Fкp, наличие связи доказано.
В нашем примере Fрасч=7,22, а Fкр=4,46
(функция F распробр при уровне значимости
0,05)
т.е. это говорит о наличии связи между объемом
выполненных работ и тарифном разряде
рабочего.
06:05
19

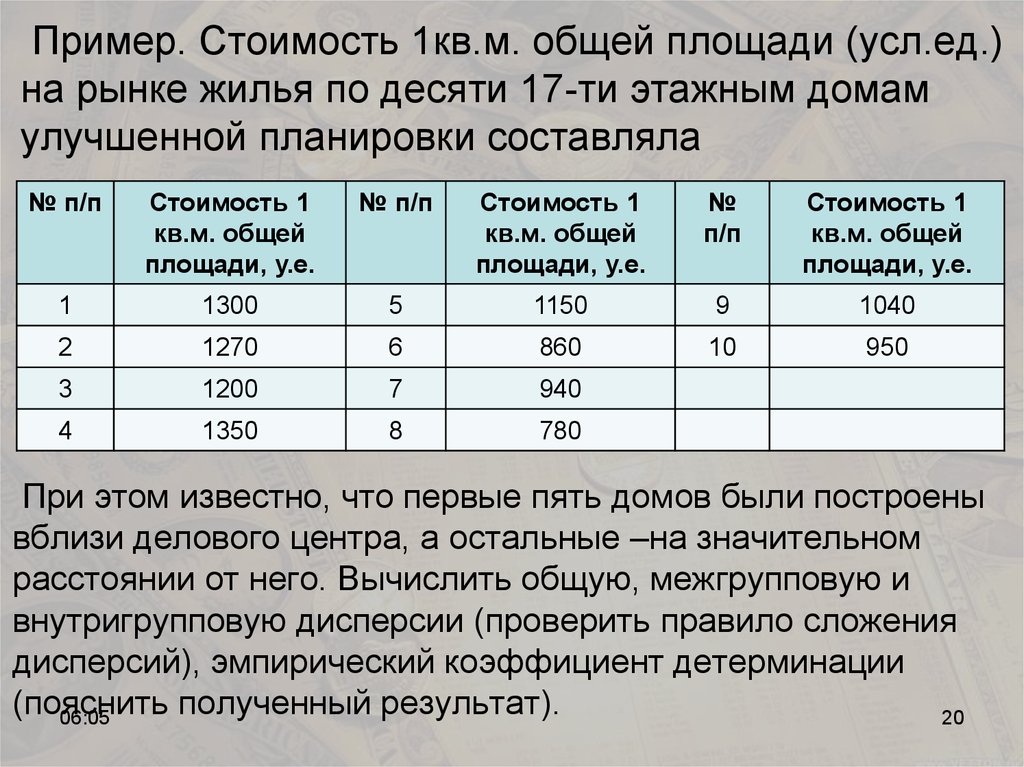
20. Пример. Стоимость 1кв.м. общей площади (усл.ед.) на рынке жилья по десяти 17-ти этажным домам улучшенной планировки составляла

№ п/п
Стоимость 1
кв.м. общей
площади, у.е.
№ п/п
Стоимость 1
кв.м. общей
площади, у.е.
№
п/п
Стоимость 1
кв.м. общей
площади, у.е.
1
1300
5
1150
9
1040
2
1270
6
860
10
950
3
1200
7
940
4
1350
8
780
При этом известно, что первые пять домов были построены
вблизи делового центра, а остальные –на значительном
расстоянии от него. Вычислить общую, межгрупповую и
внутригрупповую дисперсии (проверить правило сложения
дисперсий), эмпирический коэффициент детерминации
(пояснить
полученный результат).
06:05
20

21. Решение: Для расчета общей дисперсии вычислим среднюю стоимость 1 кв.м общей площади:

108400
x
1084 y.e.
10
Общую дисперсию определим по формуле
12103600
2
2
2
x ( x)
10842 35304
10
Вычислим среднюю стоимость 1 кв.м и дисперсию по
этому показателю для каждой группы домов,
отличающихся месторасположением относительно
центра города:
А) для домов , построенных вблизи центра:
7887900
6270
2
2
1254
5064
x1
1254
1
5
5
Б) для домов , построенных далеко от центра:
4570
4215700
2
06:05
21
x2
914
1
9142 7744
5
5

22.

Эмприческое корреляционное
отношение
свидетельствует о существенном влиянии на
стоимость жилья месторасположения домов.
06:05
22