Конденсированное состояние

1. Конденсированное состояние

ВоГУ
Лекция 9
Конденсированное
состояние
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.
1

2. План

2

3.

Реальный газ
Идеальный газ: пренебрегали
1) межмолекулярным взаимодействием
2) собственным объёмом молекул
При больших плотностях газа и при низких
температурах модель идеального газа не работает:
надо учитывать
взаимодействие молекул
собственный объём молекул
3

4.

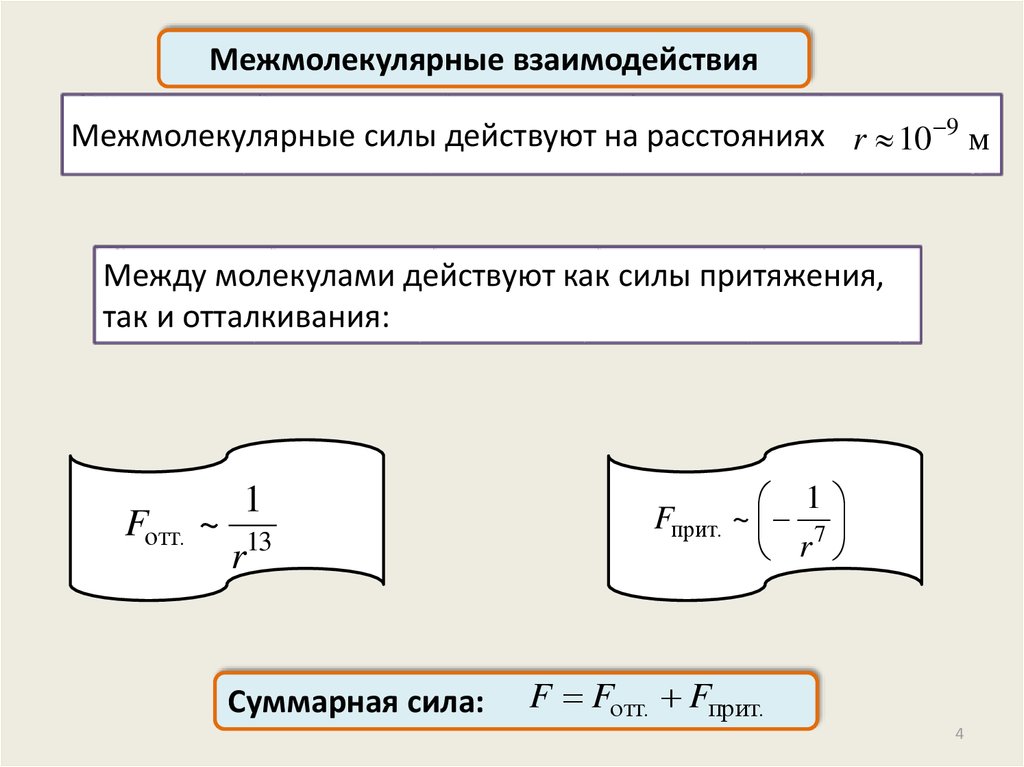
Межмолекулярные взаимодействия
Межмолекулярные силы действуют на расстояниях r 10 9 м
Между молекулами действуют как силы притяжения,
так и отталкивания:
Fотт.
1
~ 13
r
Суммарная сила:
1
Fприт. ~ 7
r
F Fотт. Fприт.
4

5.

Межмолекулярные взаимодействия
5

6.

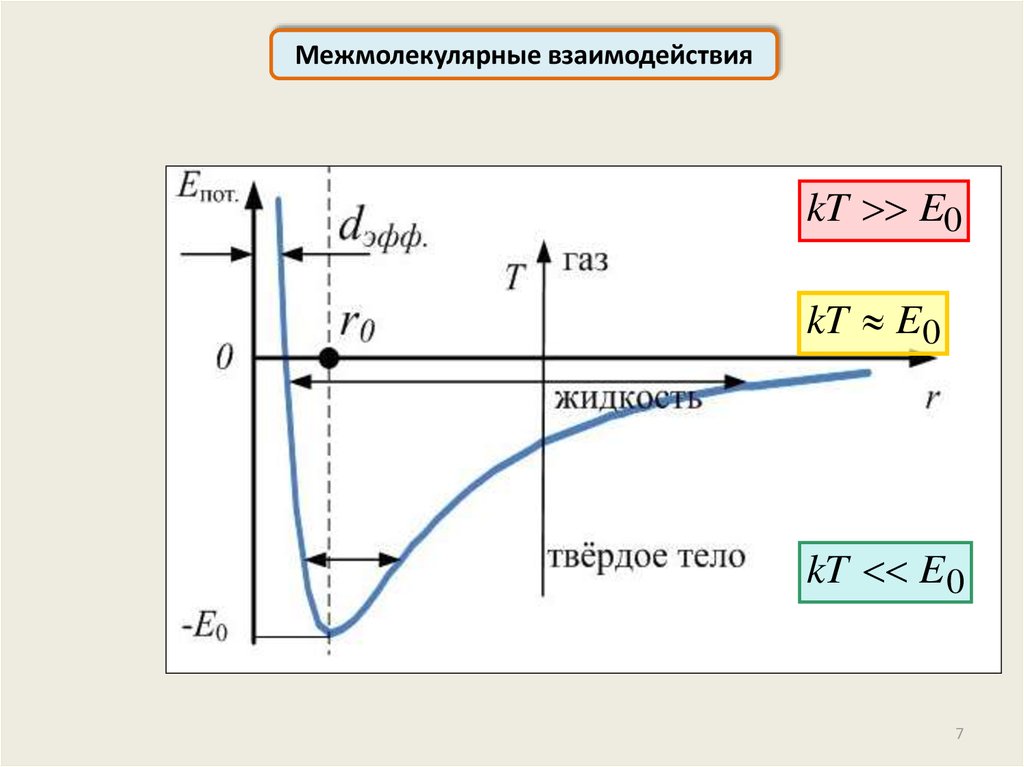
Межмолекулярные взаимодействия
Равновесное расстояние:
минимум потенциальной
энергии взаимодействия
молекул
dEпот.
F
dr
6

7.

Межмолекулярные взаимодействия
kT E0
kT E 0
kT E 0
7

8.

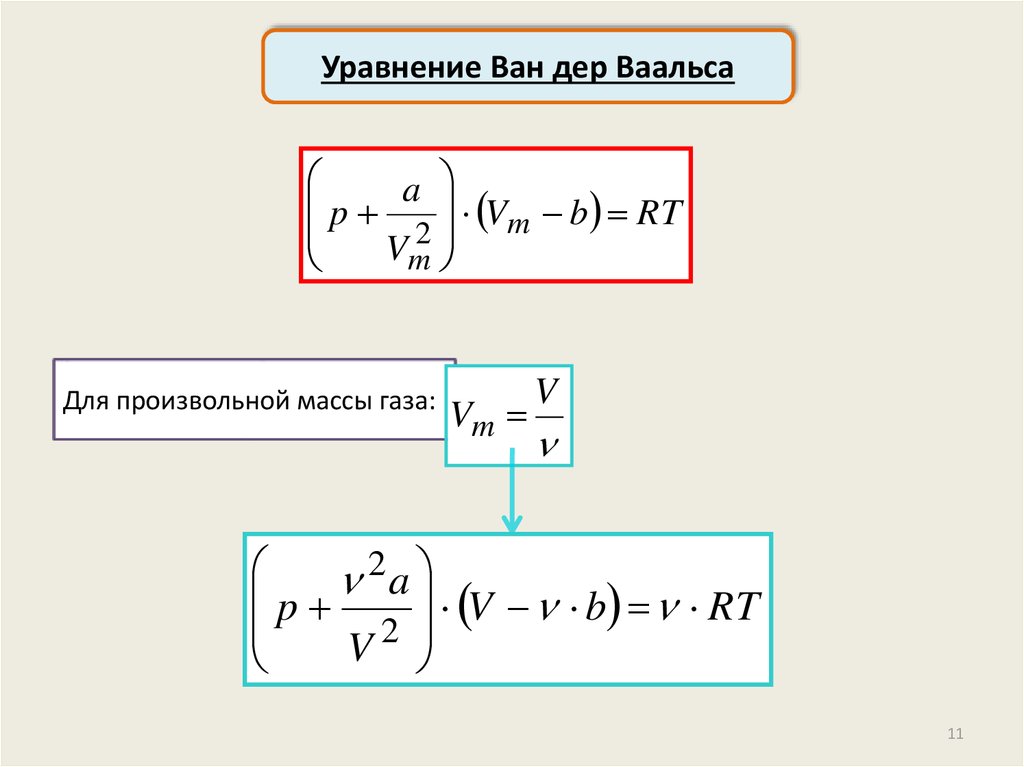
Уравнение состояния реального газа
(Уравнение Ван дер Ваальса)
Модель Ван дер Ваальса учитывает:
собственный объём молекул
взаимодействие молекул
p Vm RT
p p Vm b RT
поправка на давление
поправка на объём
8

9.

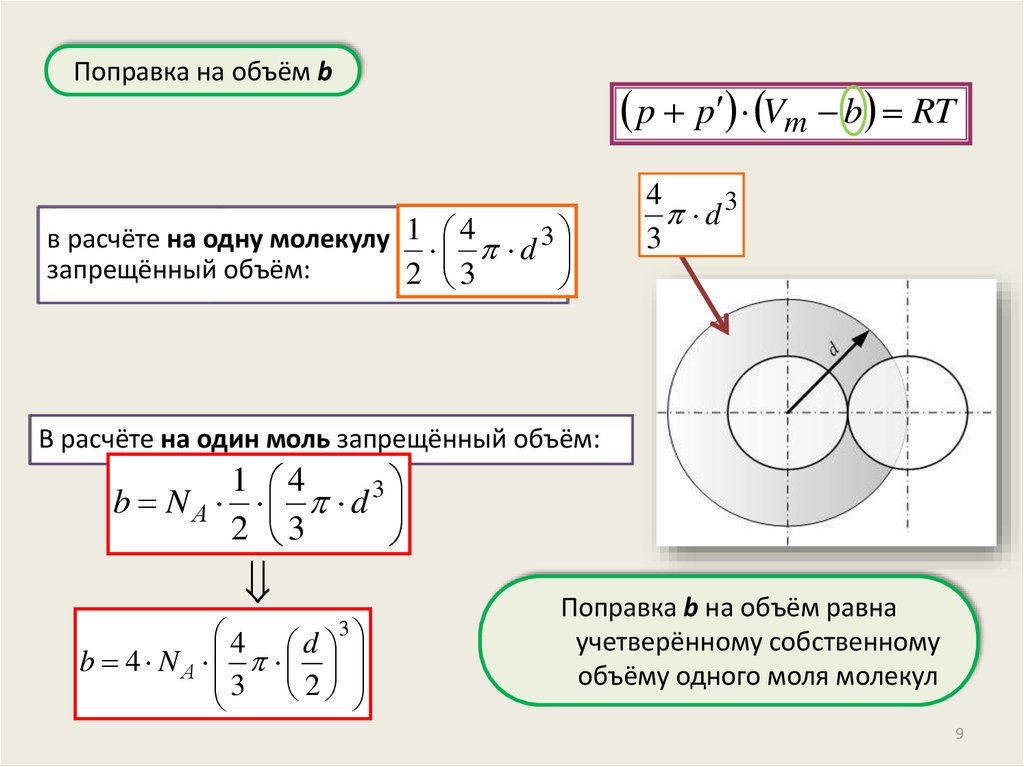
Поправка на объём b
p p Vm b RT
в расчёте на одну молекулу 1 4 d 3
запрещённый объём:
2 3
4
d3
3
В расчёте на один моль запрещённый объём:
1 4
3
b NА d
2 3
3
4 d
b 4 NА
3 2
Поправка b на объём равна
учетверённому собственному
объёму одного моля молекул
9

10.

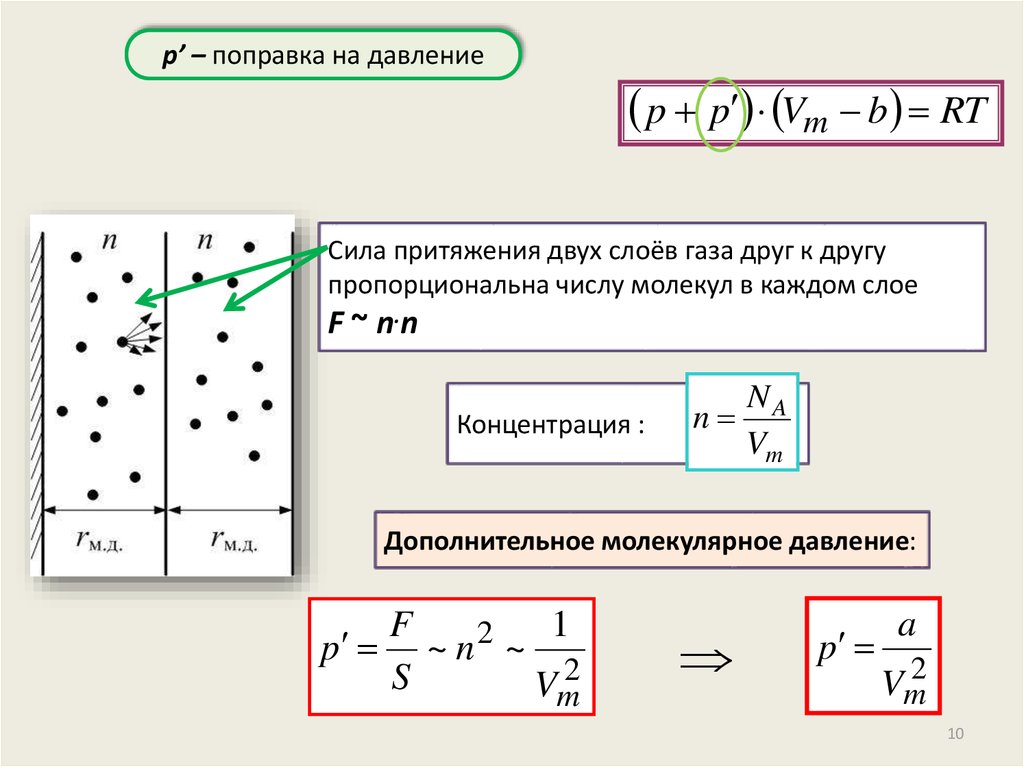
p’ – поправка на давление
p p Vm b RT
Сила притяжения двух слоёв газа друг к другу
пропорциональна числу молекул в каждом слое
F ~ n.n
Концентрация :
NA
n
Vm
Дополнительное молекулярное давление:
F
1
2
p ~ n ~
S
Vm2
p
a
Vm2
10

11.

Уравнение Ван дер Ваальса
a
p
V b RT
m
2
Vm
Для произвольной массы газа:
Vm
V
2
p a V b RT
2
V
11

12.

Уравнение Ван дер Ваальса
a
p
V b RT
m
2
Vm
Замечание 1: при высоких температурах и низких плотностях (низком
давлении) молярный объём большой:
a
p , уравнение Ван дер Ваальса переходит в
Vm >> b и
2
Vm
уравнение Менделеева-Клапейрона:
a
p
V b RT
m
2
Vm
12

13.

Уравнение Ван дер Ваальса
a
p
V b RT
m
2
Vm
Замечание 2: уравнение Ван дер Ваальса – одна из возможных моделей.
Эта модель приближённо описывает характер взаимодействия молекул:
13

14.

Изотермы реального газа. Критические параметры
Обозначение:
V Vm
a
p
V b RT
m
2
Vm
a
p
V b V 2 RT V 2
V2
p V 3 pb RT V 2 aV a b 0
14

15.

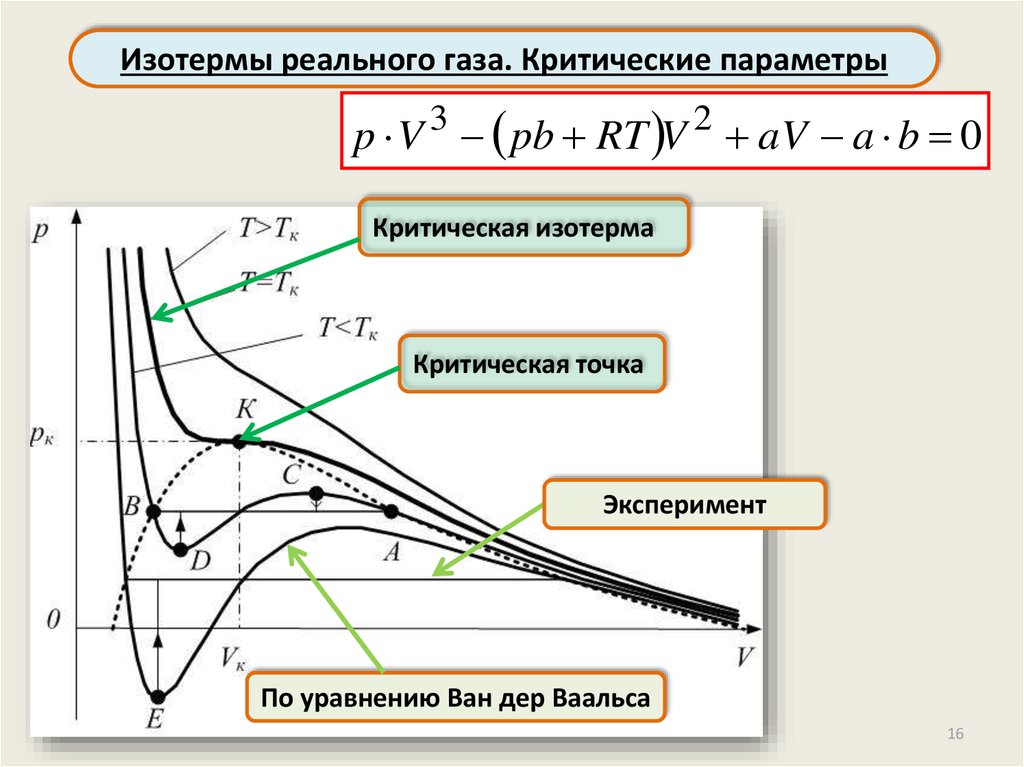
Изотермы реального газа. Критические параметры
p V 3 pb RT V 2 aV a b 0
Это уравнение третьей степени относительно объёма
В общем случае оно имеет три корня
при T=Tк все три действительных корня совпадают;
График имеет точку перегиба
Температура Tк называется критической,
как и соответствующая этой температуре изотерма.
Давление pк и молярный объём Vк реального газа,
соответствующие точке перегиба – тоже критические
15

16.

Изотермы реального газа. Критические параметры
p V 3 pb RT V 2 aV a b 0
Критическая изотерма
Критическая точка
Эксперимент
По уравнению Ван дер Ваальса
16

17.

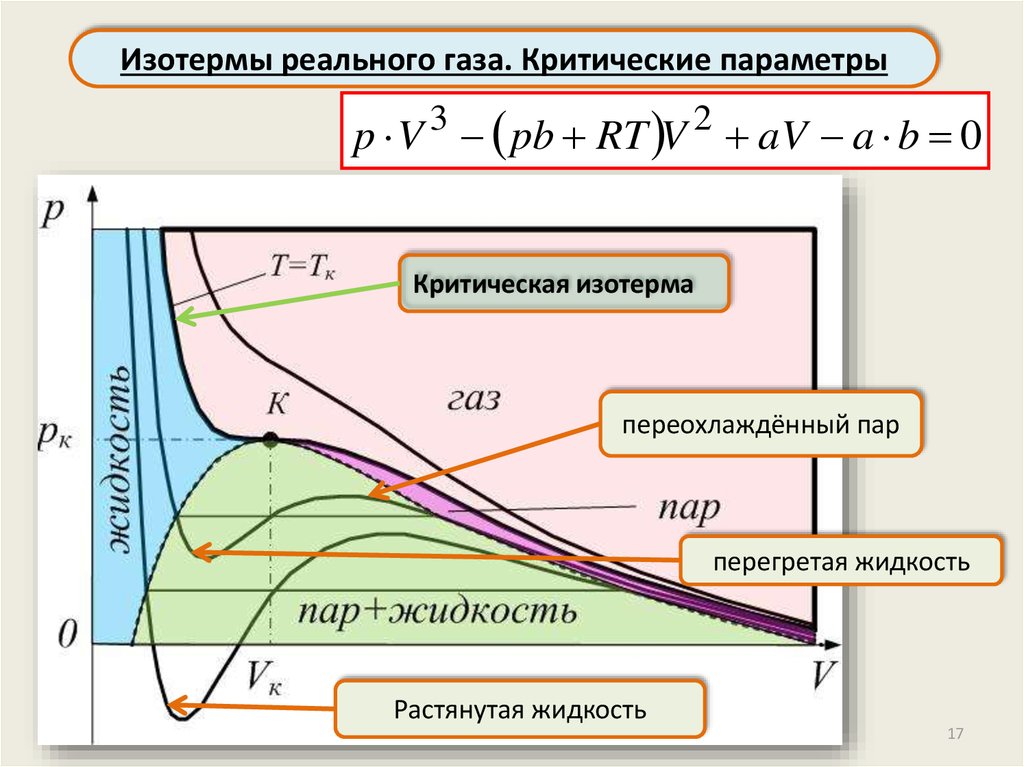
Изотермы реального газа. Критические параметры
p V 3 pb RT V 2 aV a b 0
Критическая изотерма
переохлаждённый пар
перегретая жидкость
Растянутая жидкость
17

18.

Критическое состояние
Критическое состояние – особое состояние вещества,
пограничное между паром и жидкостью
Критическая точка – точка, в которой состояния жидкости
и пара совпадают
Плотность пара равна плотности жидкости, поэтому
нет вообще границы между ними
Нет поверхностного натяжения, коэффициент
поверхностного натяжения обращается в ноль

19.

Критическое состояние
Можно найти связь между критическими параметрами
pк , Tк и Vк и поправочными коэффициентами a и b в
уравнении Ван дер Ваальса
В критической точке уравнение Ван дер Ваальса имеет три
одинаковых корня, поэтому его можно записать через куб
разности (V-Vк):
pк V Vк 0
3
19

20.

Критическое состояние
Связь между критическими параметрами pк , Tк и Vк и
поправочными коэффициентами a и b в уравнении Ван дер
Ваальса
pк V Vк 3 0
p V 3 pb RT V 2 aV a b 0
pк b RTк 3 pк Vк
2
a 3 pкVк
ab pкVк3
20

21.

Критическое состояние
pк b RTк 3 pк Vк
a 3 pкVк2
ab pкVк3
Vк 3b
a
pк
2
27
b
8a
Tк 27 R b
Vк
b
3
a 3 p V 2
к
к
21

22.

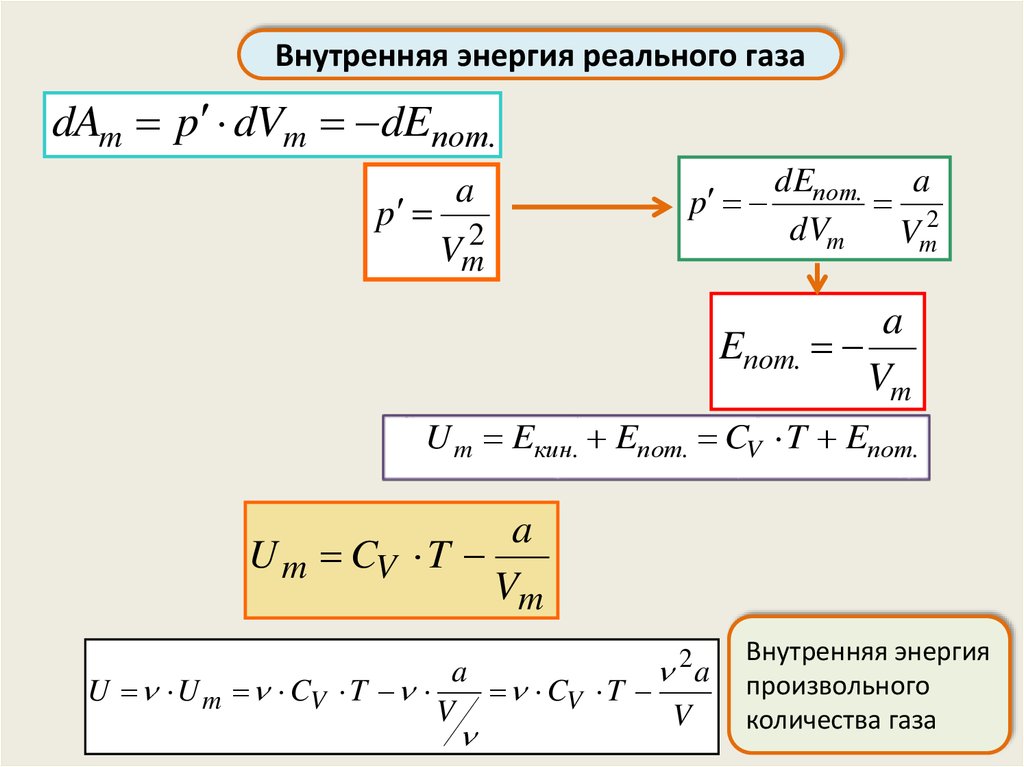
Внутренняя энергия реального газа
Внутренняя энергия реального газа равна сумме:
кинетической энергии хаотического движения молекул
потенциальной энергии взаимодействия молекул
U m Eкин. Eпот. CV T Eпот.
Силы притяжения в модели Ван дер Ваальса создают дополнительное
давление p’:
a
p
Vm2
Работа по преодолению сил притяжения при увеличении объёма на dVm
идёт на увеличение потенциальной энергии:
dAm p dVm dEпот.
22

23.

Внутренняя энергия реального газа
dAm p dVm dEпот.
p
a
Vm2
dEпот. a
p
2
dVm
Vm
a
Eпот.
Vm
U m Eкин. Eпот. CV T Eпот.
a
U m CV T
Vm
a
a
U U m CV T
CV T
V
V
2
Внутренняя энергия
произвольного
количества газа 23

24.

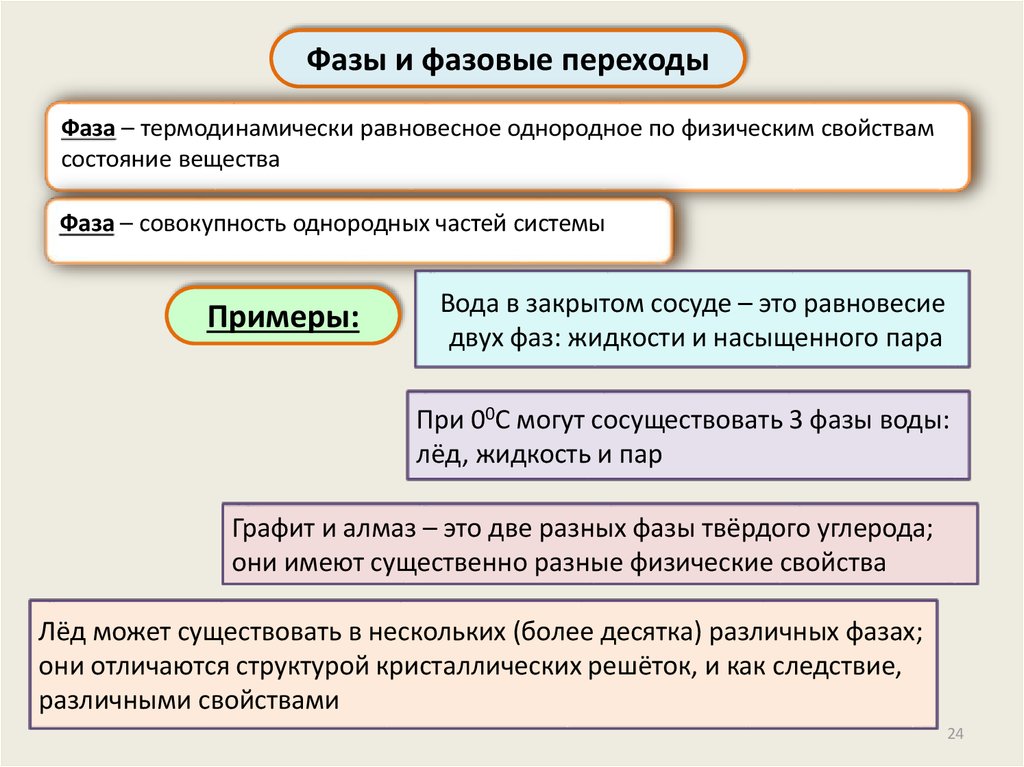
Фазы и фазовые переходы
Фаза – термодинамически равновесное однородное по физическим свойствам
состояние вещества
Фаза – совокупность однородных частей системы
Примеры:
Вода в закрытом сосуде – это равновесие
двух фаз: жидкости и насыщенного пара
При 00С могут сосуществовать 3 фазы воды:
лёд, жидкость и пар
Графит и алмаз – это две разных фазы твёрдого углерода;
они имеют существенно разные физические свойства
Лёд может существовать в нескольких (более десятка) различных фазах;
они отличаются структурой кристаллических решёток, и как следствие,
различными свойствами
24

25.

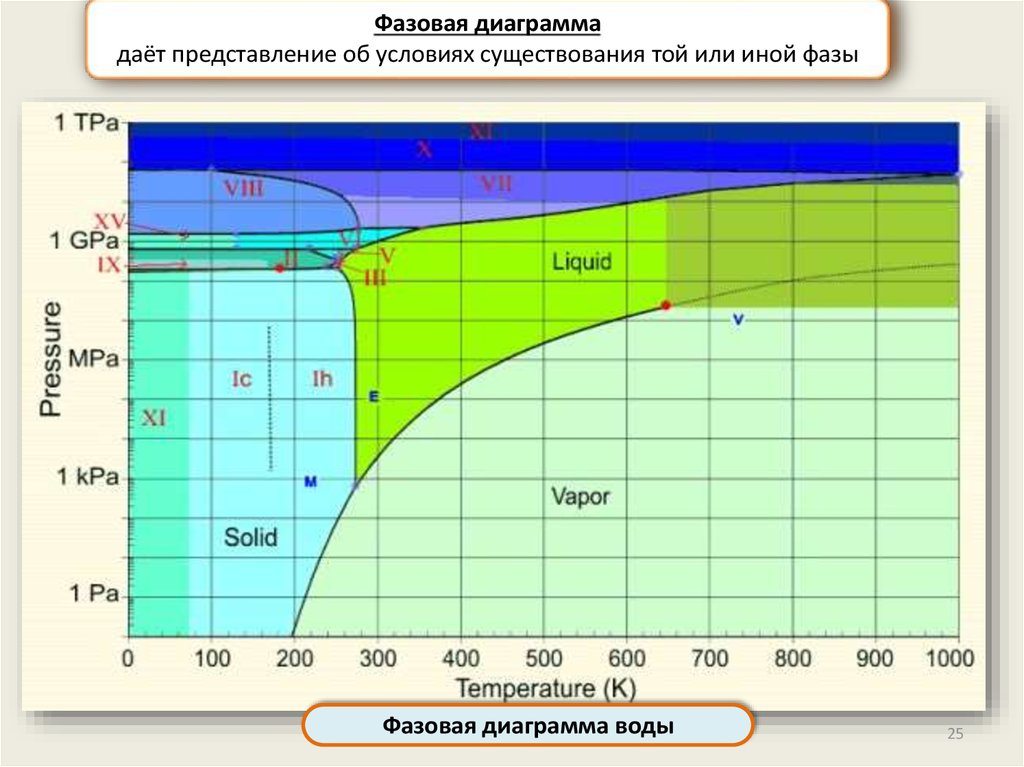
Фазовая диаграмма
даёт представление об условиях существования той или иной фазы
Фазовая диаграмма воды
25

26.

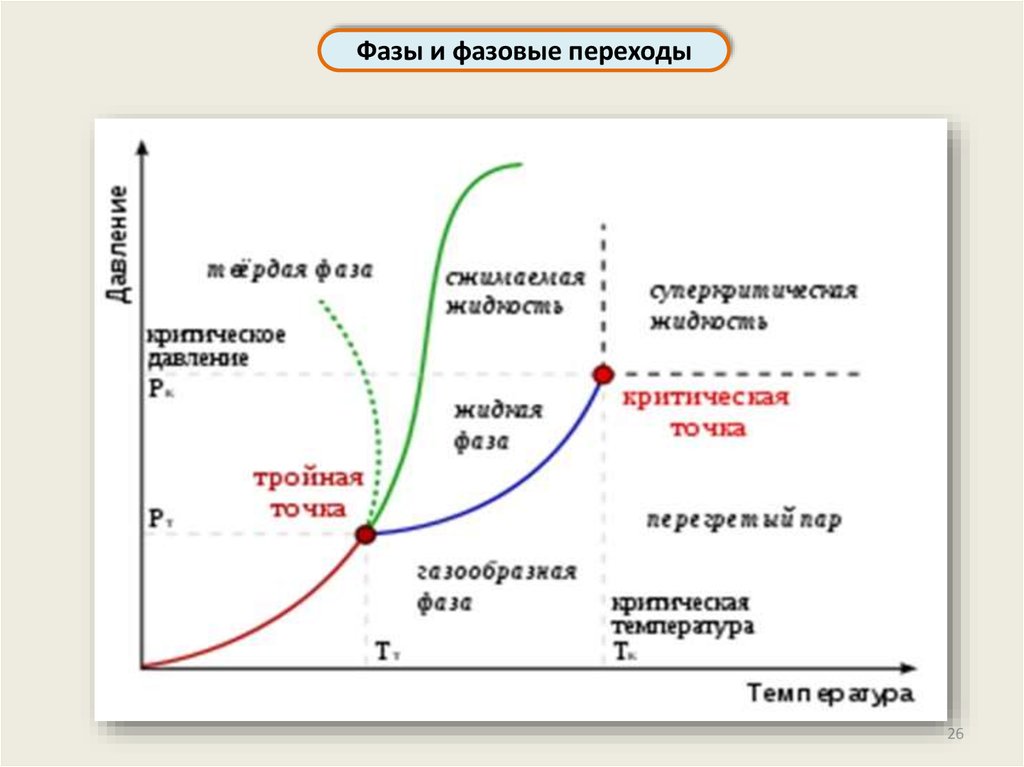
Фазы и фазовые переходы
26

27.

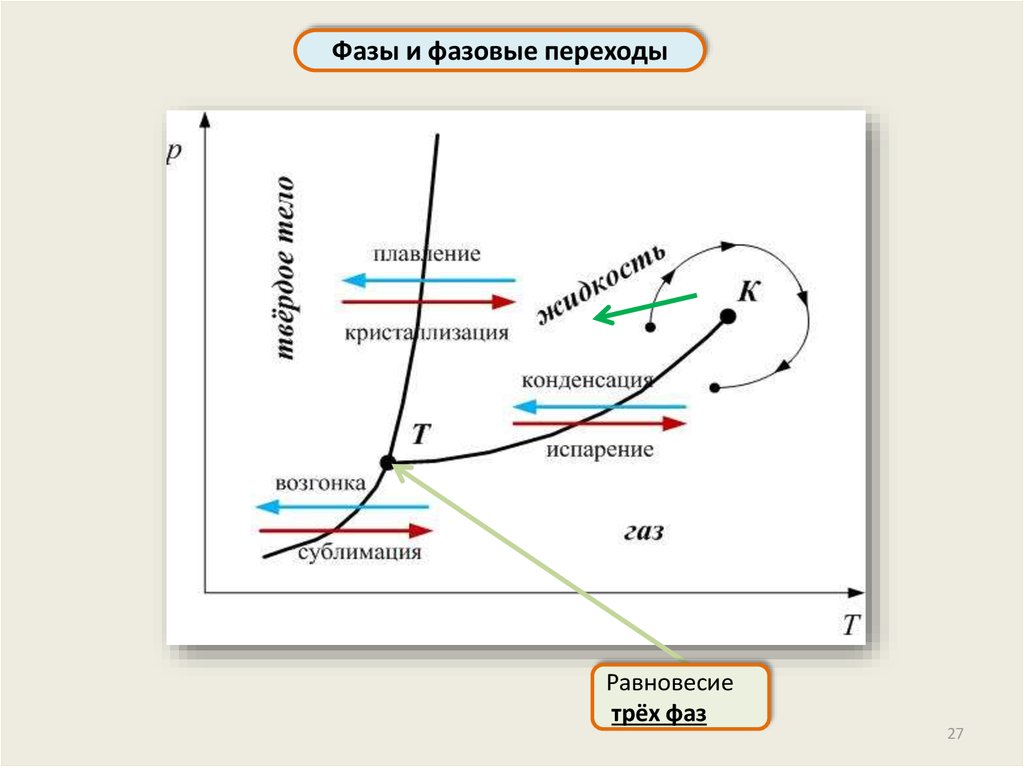
Фазы и фазовые переходы
Равновесие
трёх фаз
27

28.

Фазы и фазовые переходы
Фазовым переходом первого рода называется
фазовый переход с поглощением или выделением
теплоты
Все агрегатные превращения – это фазовые переходы
первого рода:
парообразование, конденсация, сублимация, возгонка,
кристаллизация, плавление
Фазовый переход первого рода сопровождается резким изменением плотности
вещества
При фазовых переходах первого рода теплоёмкость вещества обращается в
бесконечность: C
Q
dT
, поскольку теплота поглощается (выделяется) ,
а температура не изменяется
28

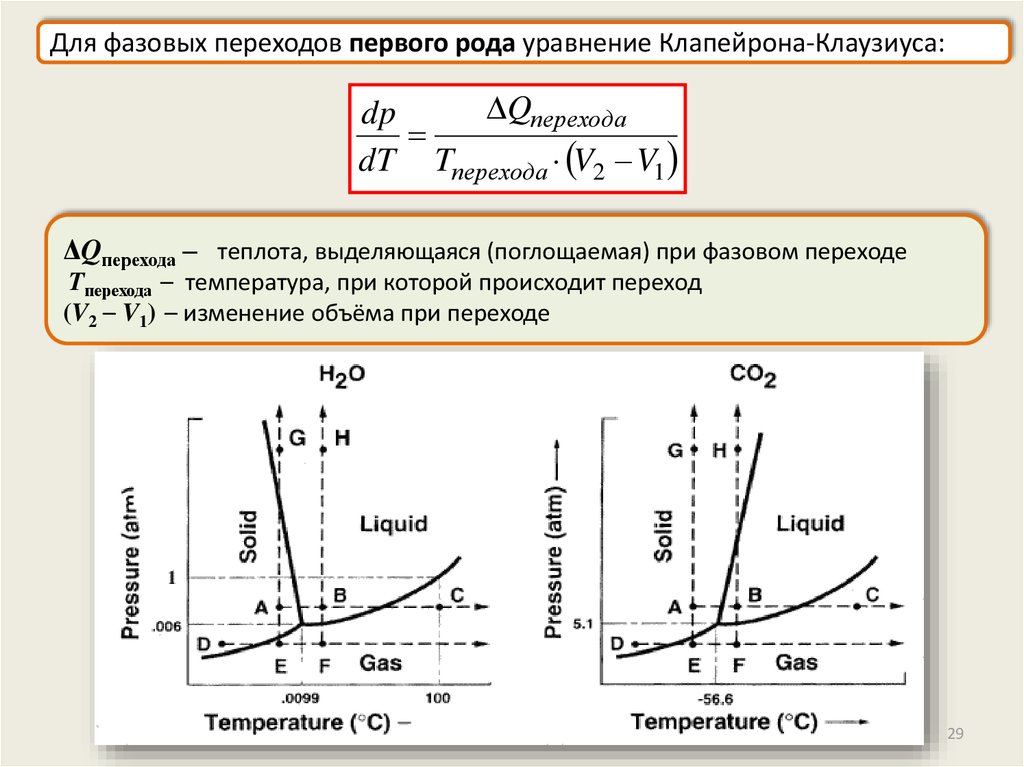
29.

Для фазовых переходов первого рода уравнение Клапейрона-Клаузиуса:
Qперехода
dp
dT Tперехода V2 V1
ΔQперехода – теплота, выделяющаяся (поглощаемая) при фазовом переходе
Tперехода – температура, при которой происходит переход
(V2 – V1) – изменение объёма при переходе
29

30.

Фазы и фазовые переходы
Фазовый переход второго рода
не сопровождается поглощением или выделением теплоты
При фазовых переходах второго рода
скачкообразно меняются свойства вещества:
теплоёмкость, вязкость, ферромагнитные свойства,
электрические свойства…
Примеры фазовых переходов второго рода:
переход ферромагнетик-неферромагнетик при температуре Кюри
переход в сверхпроводящее состояние при сверхнизких температурах
переход жидкого гелия в сверхтекучее состояние при сверхнизких
температурах
переход кристалла из одной модификации в другую (металлы, графиталмаз, лёд и т.д.)
полимерные переходы жидких кристаллов; при этом меняются
оптические свойства
30

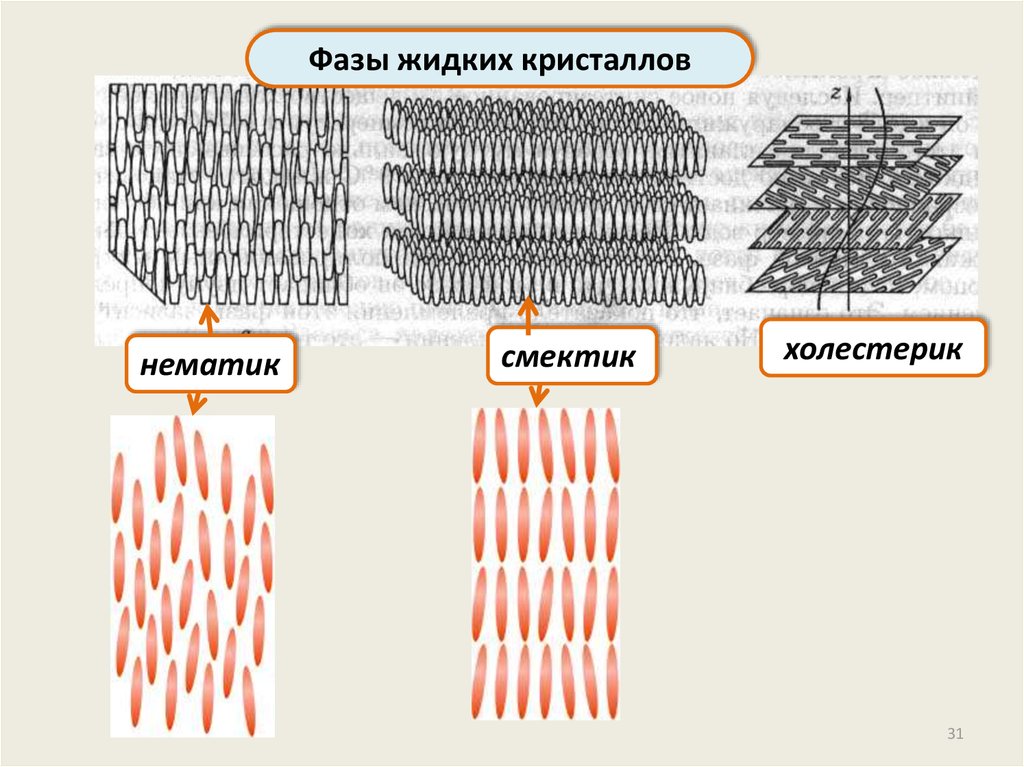
31.

Фазы жидких кристаллов
нематик
смектик
холестерик
31

32.

Жидкое состояние
Газ
kT E0
Газ занимает
весь объём
Молекулы
движутся
хаотично
– промежуточное между газом и твёрдым телом:
сочетает свойства того и другого.
Жидкость
kT E0
Силы притяжения удерживают
частицы на определённых
расстояниях друг от друга
Молекулы жидкости колеблются
около своего положения
равновесия в течение некоторого
времени. Затем перескакивают в
соседнее положение равновесия
Ближний порядок в расположении
частиц: упорядоченность на
небольших расстояниях,
сравнимых с межатомными
Твёрдое тело
kT E0
Сохраняет не только
объём, но и форму
Частицы колеблются
около своего положения
равновесия
Дальний порядок в
расположении частиц:
упорядоченность
сохраняется на больших
расстояниях
32

33.

Жидкое состояние
Теории жидкости, объясняющей все её свойства, нет.
Некоторые проблемы жидкости разработаны Френкелем.
По его теории, молекулы жидкости колеблются около своего положения
равновесия в течение некоторого времени, которое называется временем
оседлой жизни.
Затем перескакивают в соседнее положение равновесия. Время оседлой
жизни примерно равно τ≈10-12÷10-10 с и сильно зависит от температуры:
E
e
0
пот
kT
Тепловое движение молекул жидкости носит групповой характер
С возрастанием температуры молекулы становятся более подвижными
33

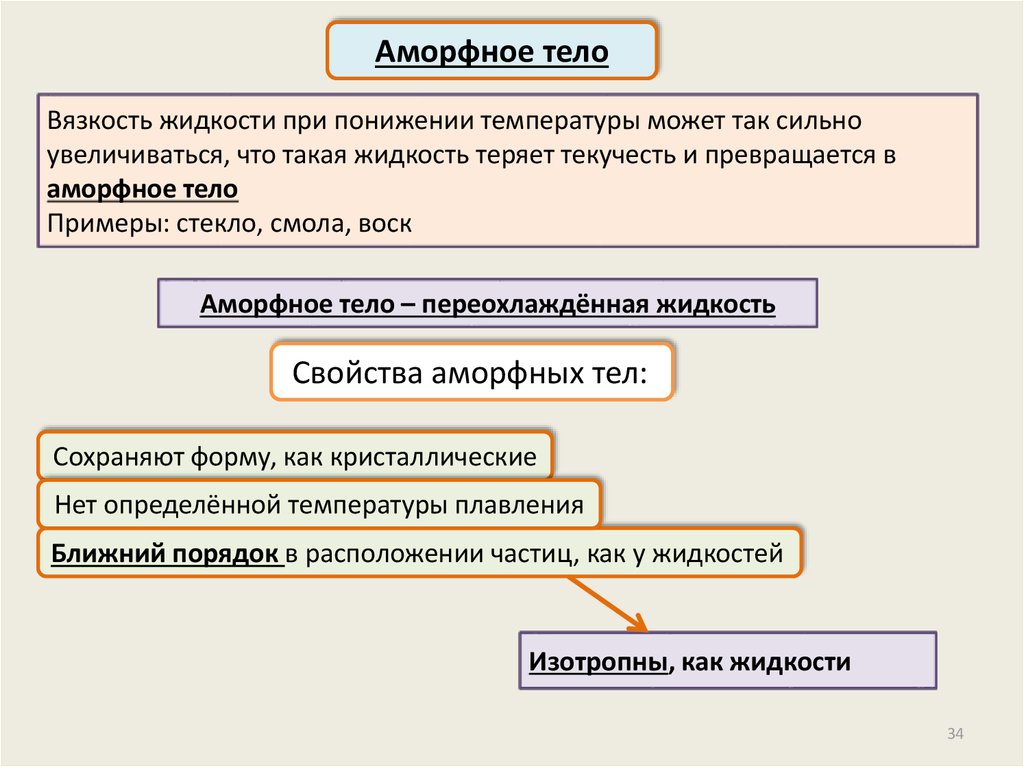
34.

Аморфное тело
Вязкость жидкости при понижении температуры может так сильно
увеличиваться, что такая жидкость теряет текучесть и превращается в
аморфное тело
Примеры: стекло, смола, воск
Аморфное тело – переохлаждённая жидкость
Свойства аморфных тел:
Сохраняют форму, как кристаллические
Нет определённой температуры плавления
Ближний порядок в расположении частиц, как у жидкостей
Изотропны, как жидкости
34

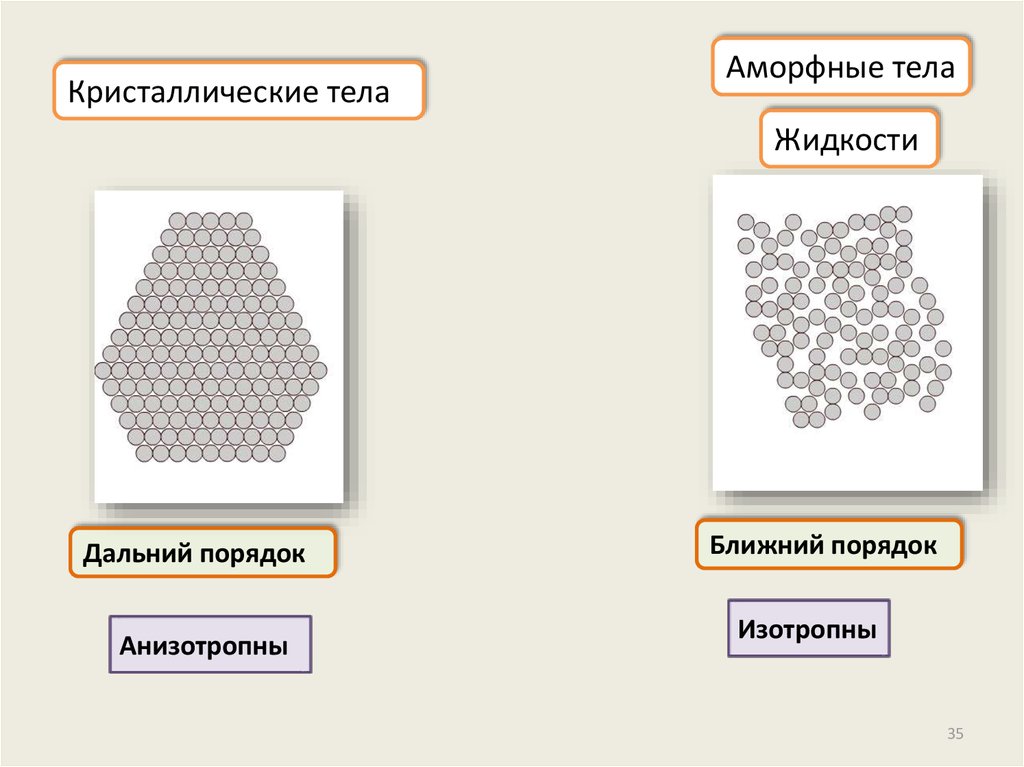
35.

Кристаллические тела
Аморфные тела
Жидкости
Дальний порядок
Анизотропны
Ближний порядок
Изотропны
35

36.

Жидкие кристаллы
В жидких кристаллах в пределах значительного объёма
наблюдается одинаковая ориентация молекул (если, например,
молекулы длинные с боковыми отростками)
ЖК анизотропны
Дальнего порядка в ЖК может и не быть
36

37.

Поверхностное натяжение
Радиус молекулярного действия
rмд 10 9 м
Сфера молекулярного действия – сфера с радиусом, равным радиусу
молекулярного действия.
Любая молекула, находящаяся в сфере молекулярного действия данной
молекулы, взаимодействует с ней (притягивается); вне сферы – не
взаимодействует с ней
rм.д.
r>rм.д.

38.

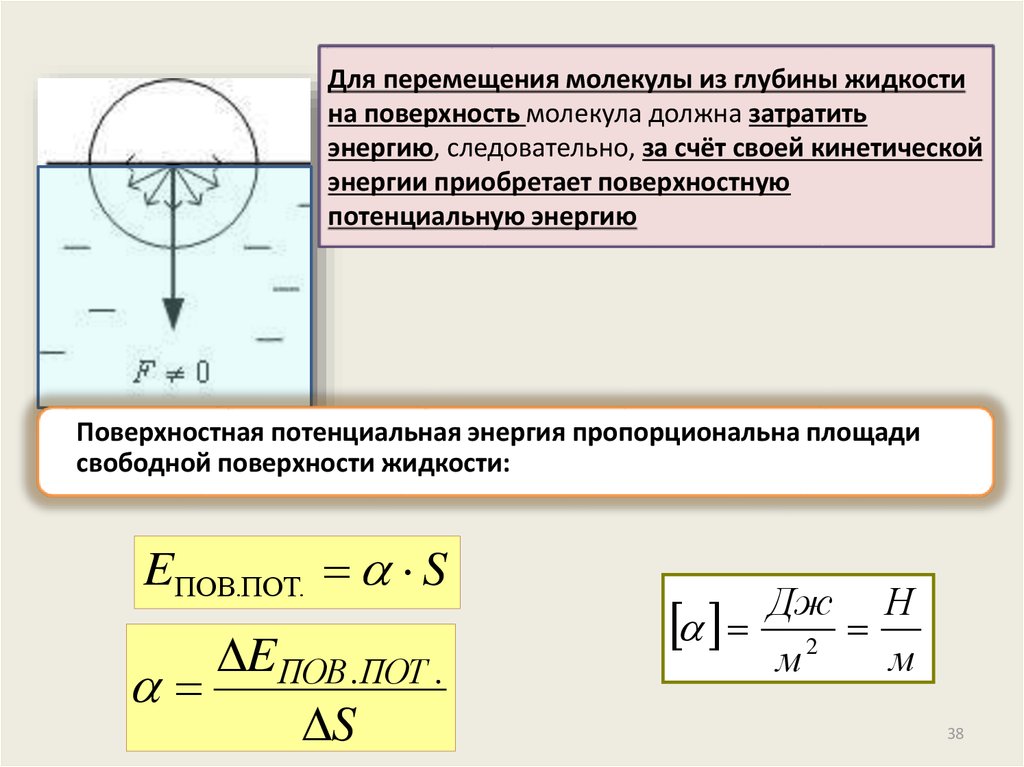
Для перемещения молекулы из глубины жидкости
на поверхность молекула должна затратить
энергию, следовательно, за счёт своей кинетической
энергии приобретает поверхностную
потенциальную энергию
Поверхностная потенциальная энергия пропорциональна площади
свободной поверхности жидкости:
EПОВ.ПОТ. S
EПОВ .ПОТ .
S
Дж Н
2
м
м
38

39.

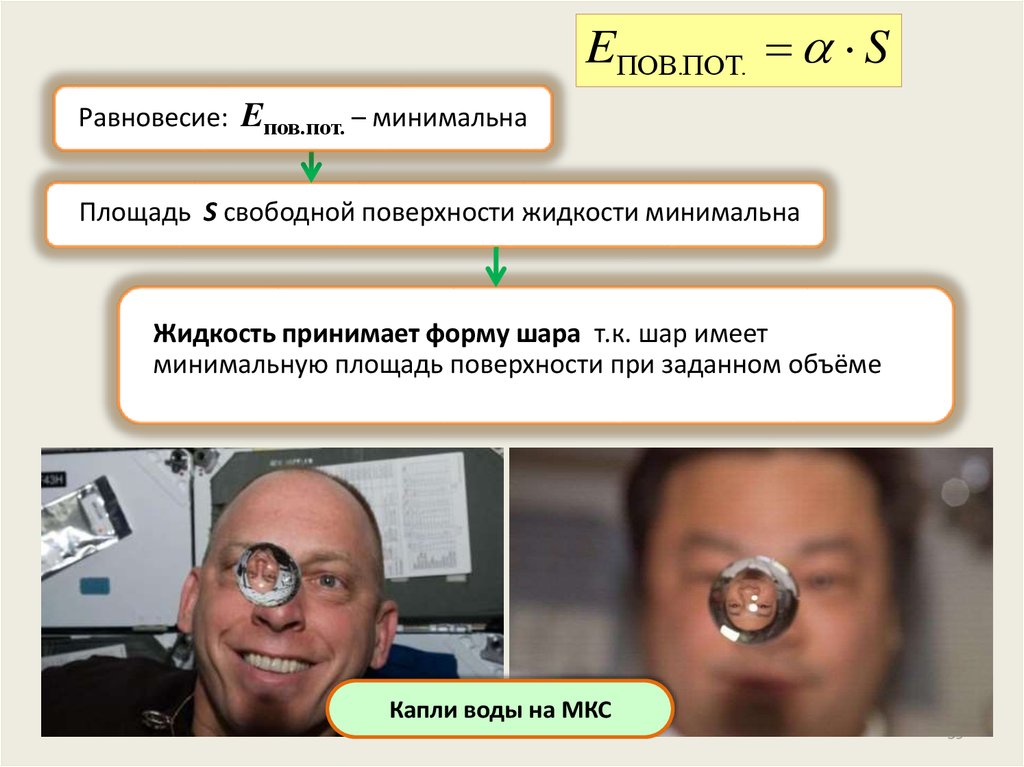
EПОВ.ПОТ. S
Равновесие: Eпов.пот. – минимальна
Площадь S свободной поверхности жидкости минимальна
Жидкость принимает форму шара т.к. шар имеет
минимальную площадь поверхности при заданном объёме
Капли воды на МКС
39

40.

Работа, совершаемая при перемещении контура на dx:
dA Fdx
dA dEПОВ.ПОТ.
dEПОВ.ПОТ. dS
dS l dx
Fdx l dx
F
l
α - коэффициент поверхностного натяжения численно равен силе
поверхностного натяжения, приходящейся на единицу длины контура
40

41.

Давление под искривлённой поверхностью.
Формула Лапласа
Поверхностная плёнка стремится к сокращению → создаётся
дополнительное давление Δp на жидкость по сравнению с
плоской поверхностью
41

42.

Формула Лапласа
Найдём избыточное давление Δp для выпуклой сферической поверхности с
радиусом кривизны R и радиусом сегмента r :
FП.Н. l 2 r
Fy FП.Н. cos
2
2 r cos 2 cos
p
p
R
S
r
r2
2
S r
R cos r
Fy
42

43.

Давление под сферической поверхностью:
Выпуклая:
Вогнутая:
R>0, Δp>0
R<0, Δp<0
2
p
R
Для плоской поверхностиR=0, Δp=0
Для произвольной поверхности любой формы – формула Лапласа:
1
1
p
R1 R2 43

44.

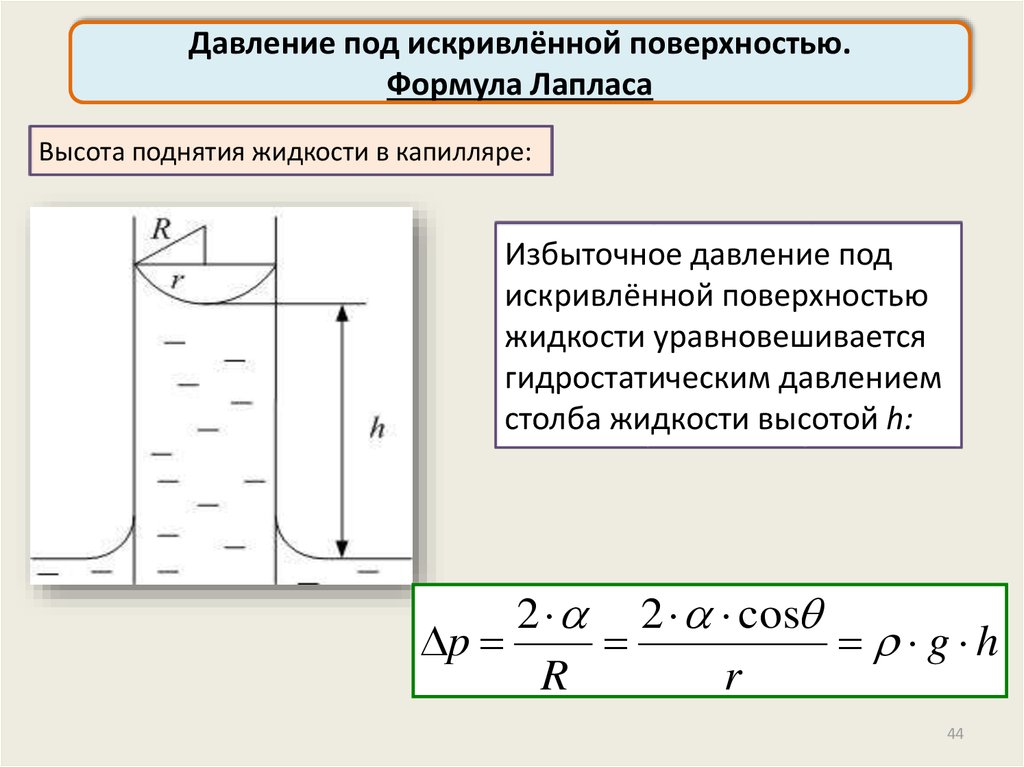
Давление под искривлённой поверхностью.
Формула Лапласа
Высота поднятия жидкости в капилляре:
Избыточное давление под
искривлённой поверхностью
жидкости уравновешивается
гидростатическим давлением
столба жидкости высотой h:
2 2 cos
p
g h
R
r
44

45.

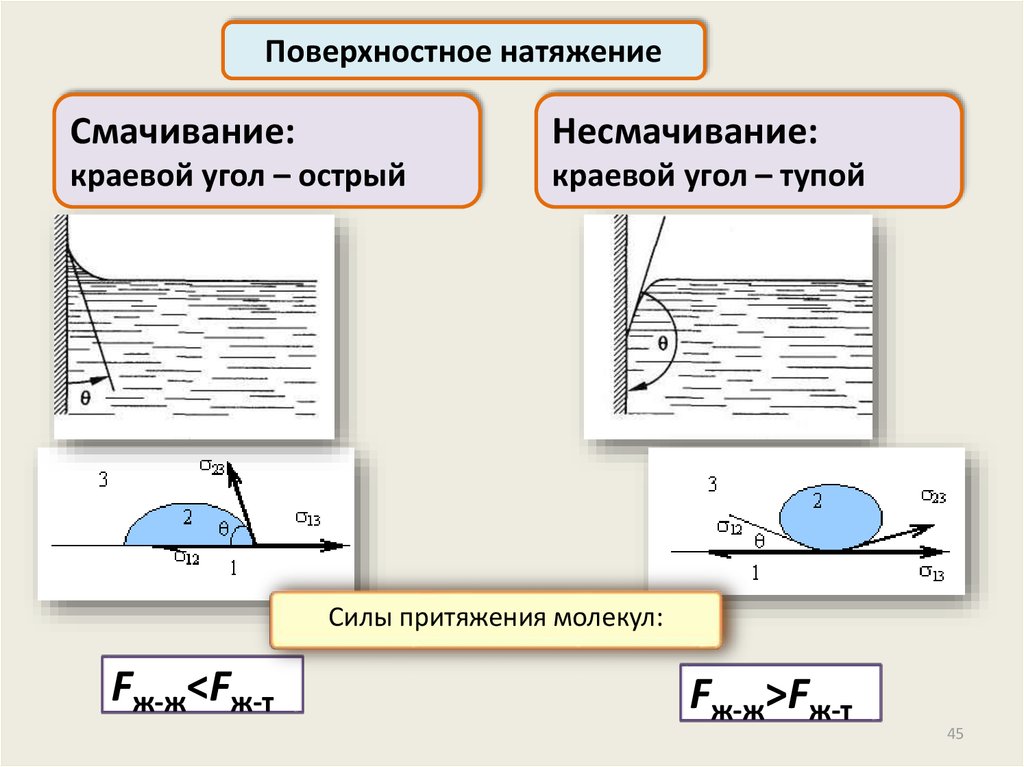
Поверхностное натяжение
Смачивание:
Несмачивание:
краевой угол – острый
краевой угол – тупой
Силы притяжения молекул:
Fж-ж<Fж-т
Fж-ж>Fж-т
45

46.

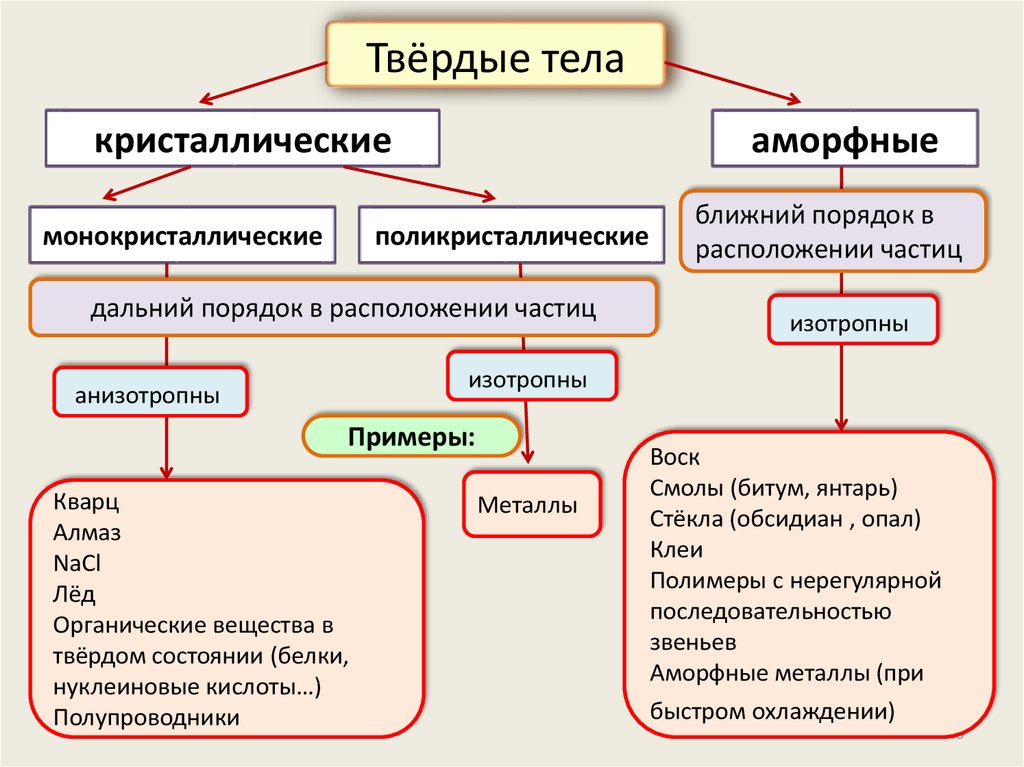
Твёрдые тела
кристаллические
монокристаллические
аморфные
поликристаллические
дальний порядок в расположении частиц
ближний порядок в
расположении частиц
изотропны
изотропны
анизотропны
Примеры:
Кварц
Алмаз
NaCl
Лёд
Органические вещества в
твёрдом состоянии (белки,
нуклеиновые кислоты…)
Полупроводники
Металлы
Воск
Смолы (битум, янтарь)
Стёкла (обсидиан , опал)
Клеи
Полимеры с нерегулярной
последовательностью
звеньев
Аморфные металлы (при
быстром охлаждении)
46

47.

Твёрдые тела
кристаллические
дальний порядок в
расположении частиц
аморфные
ближний порядок в
расположении частиц
47

48.

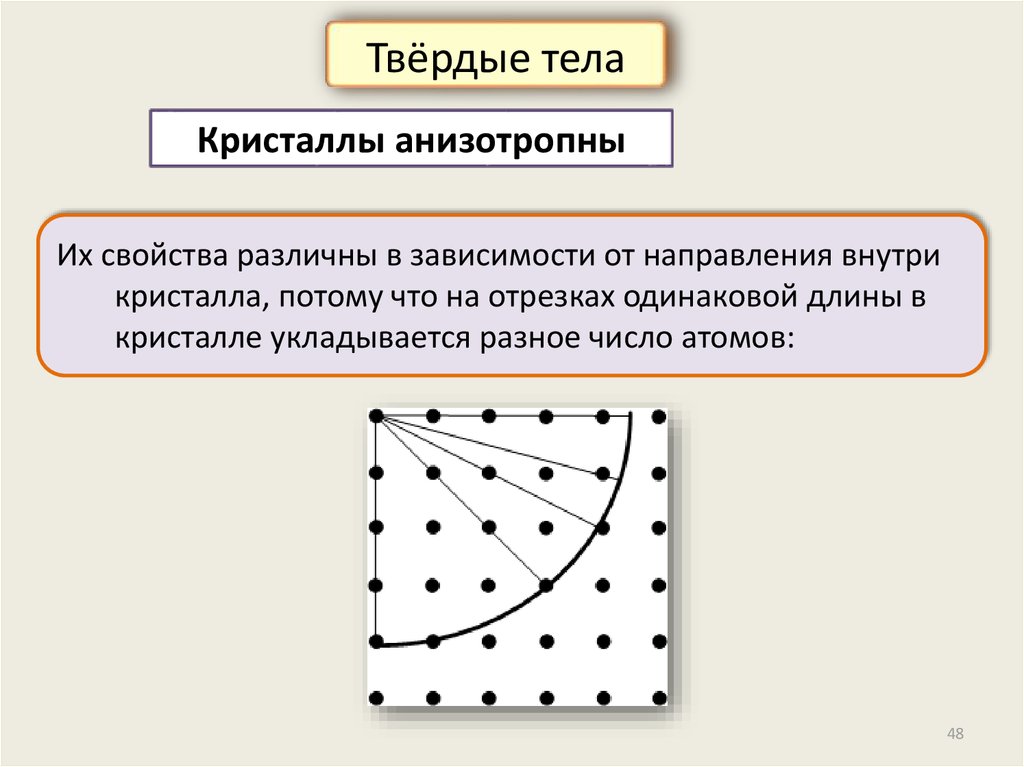
Твёрдые тела
Кристаллы анизотропны
Их свойства различны в зависимости от направления внутри
кристалла, потому что на отрезках одинаковой длины в
кристалле укладывается разное число атомов:
48

49.

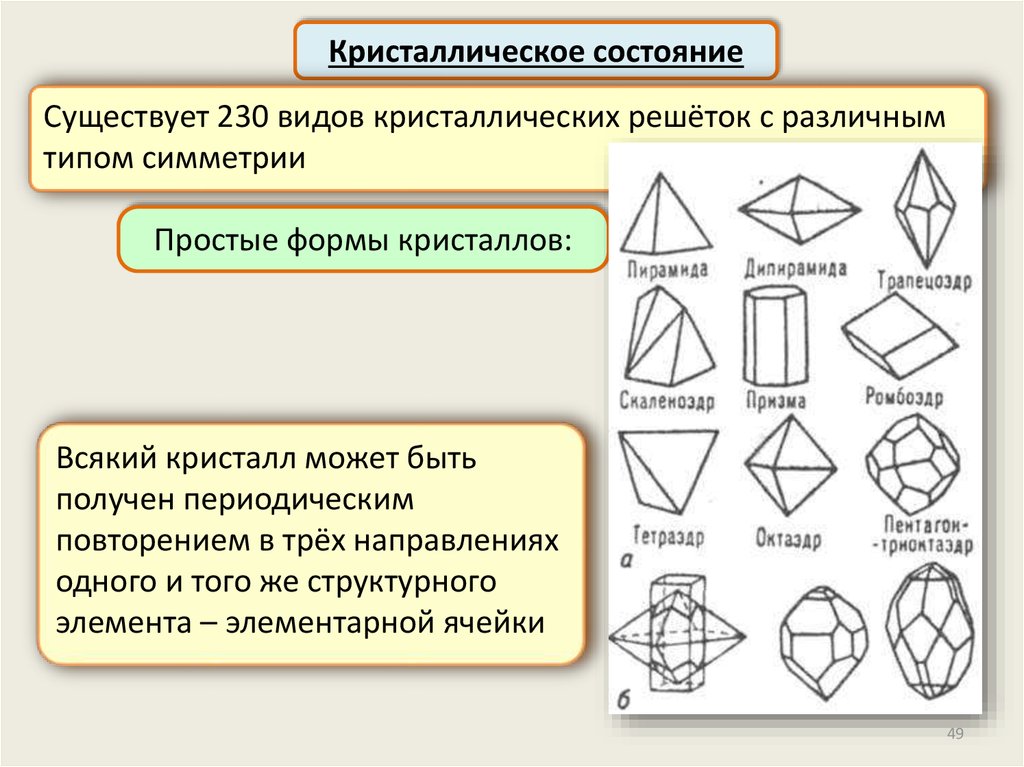
Кристаллическое состояние
Существует 230 видов кристаллических решёток с различным
типом симметрии
Простые формы кристаллов:
Всякий кристалл может быть
получен периодическим
повторением в трёх направлениях
одного и того же структурного
элемента – элементарной ячейки
49

50.

51.

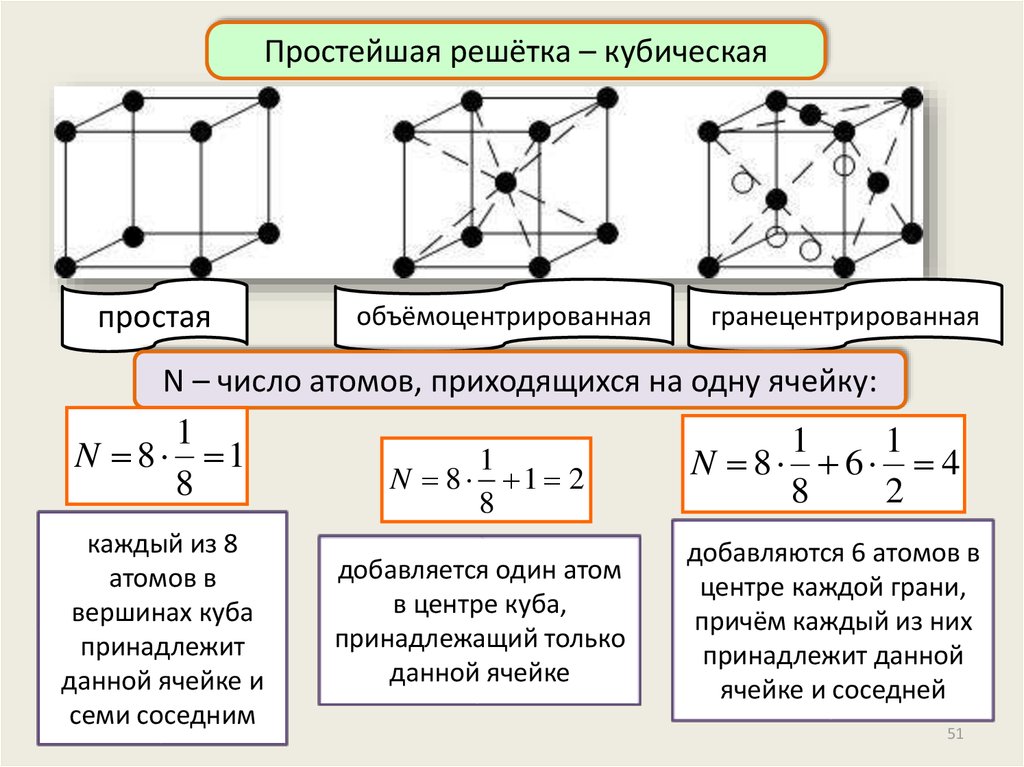
Простейшая решётка – кубическая
простая
объёмоцентрированная
гранецентрированная
N – число атомов, приходящихся на одну ячейку:
1
N 8 1
8
каждый из 8
атомов в
вершинах куба
принадлежит
данной ячейке и
семи соседним
1
N 8 1 2
8
добавляется один атом
в центре куба,
принадлежащий только
данной ячейке
1
1
N 8 6 4
8
2
добавляются 6 атомов в
центре каждой грани,
причём каждый из них
принадлежит данной
ячейке и соседней
51

52.

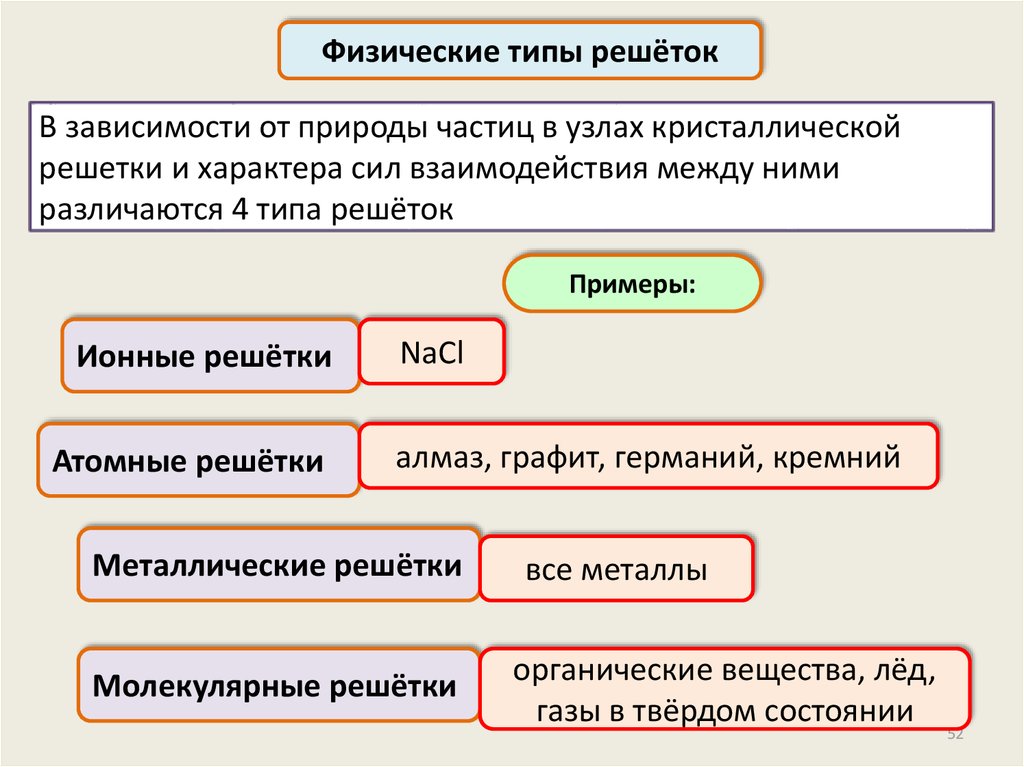
Физические типы решёток
В зависимости от природы частиц в узлах кристаллической
решетки и характера сил взаимодействия между ними
различаются 4 типа решёток
Примеры:
Ионные решётки
Атомные решётки
NaCl
алмаз, графит, германий, кремний
Металлические решётки
Молекулярные решётки
все металлы
органические вещества, лёд,
газы в твёрдом состоянии
52

53.

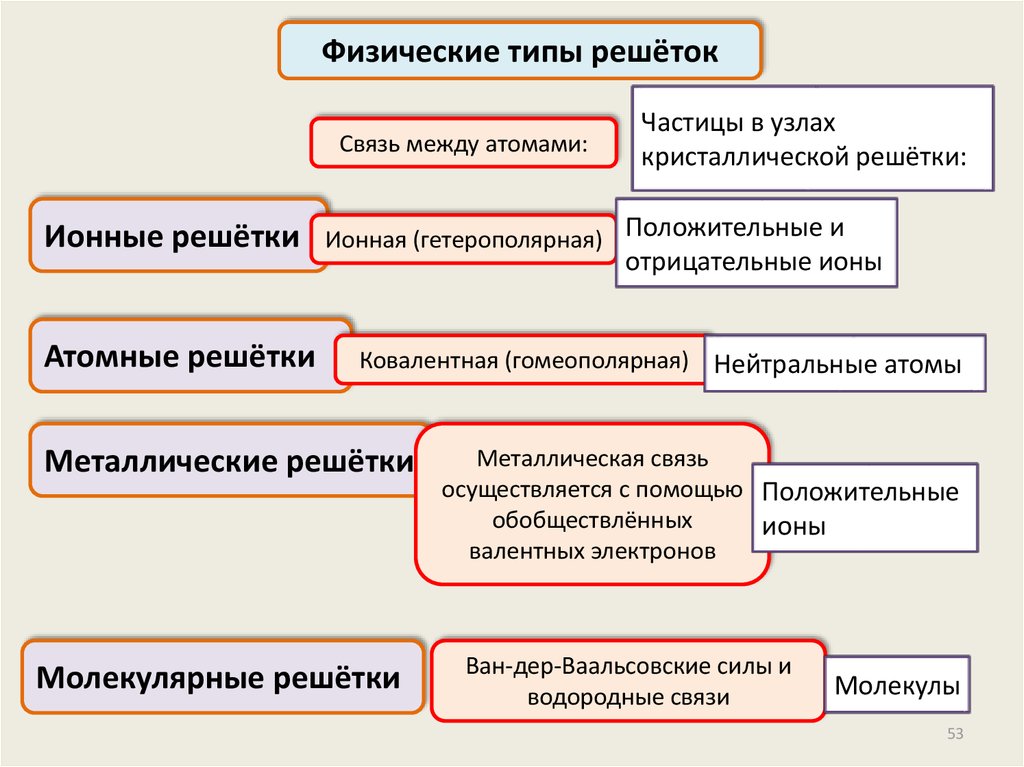
Физические типы решёток
Связь между атомами:
Ионные решётки
Атомные решётки
Частицы в узлах
кристаллической решётки:
Ионная (гетерополярная) Положительные и
отрицательные ионы
Ковалентная (гомеополярная) Нейтральные атомы
Металлические решётки
Молекулярные решётки
Металлическая связь
осуществляется с помощью Положительные
обобществлённых
ионы
валентных электронов
Ван-дер-Ваальсовские силы и
водородные связи
Молекулы
53

54.

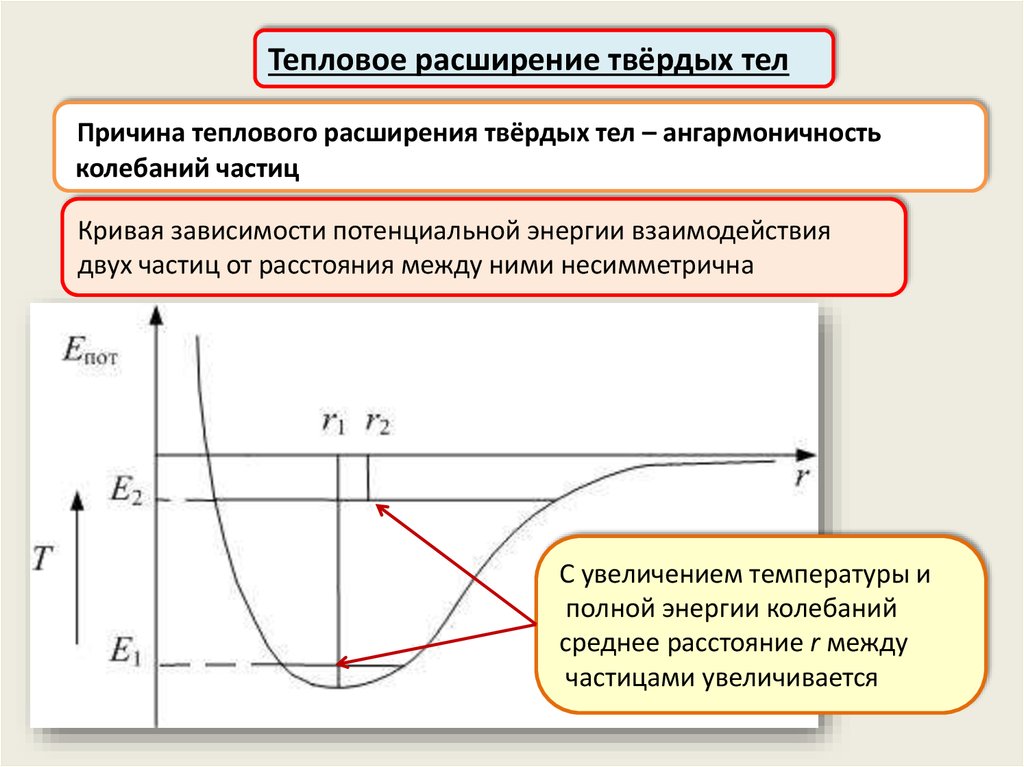
Тепловое расширение твёрдых тел
Причина теплового расширения твёрдых тел – ангармоничность
колебаний частиц
Кривая зависимости потенциальной энергии взаимодействия
двух частиц от расстояния между ними несимметрична
С увеличением температуры и
полной энергии колебаний
среднее расстояние r между
частицами увеличивается

55.

Тепловое расширение твёрдых тел
Линейные размеры тела при температуре t0 C равны:
l l0 1 t
Изменение длины при нагревании: l l l0 l0 t
l
l0 T
Коэффициент линейного теплового расширения α численно равен
относительному увеличению длины тела при нагревании на 10 С
1
1
K град

56.

Объём тела при температуре t0 C равен:
V V0 1 t
Изменение объёма при нагревании: V V V0 V0 t
V
V0 T
1
1
K град
Коэффициент объёмного теплового расширения β численно равен
относительному увеличению объёма тела при нагревании на 10 С
Для аморфных тел и кристаллов с кубической решёткой:
3

57.

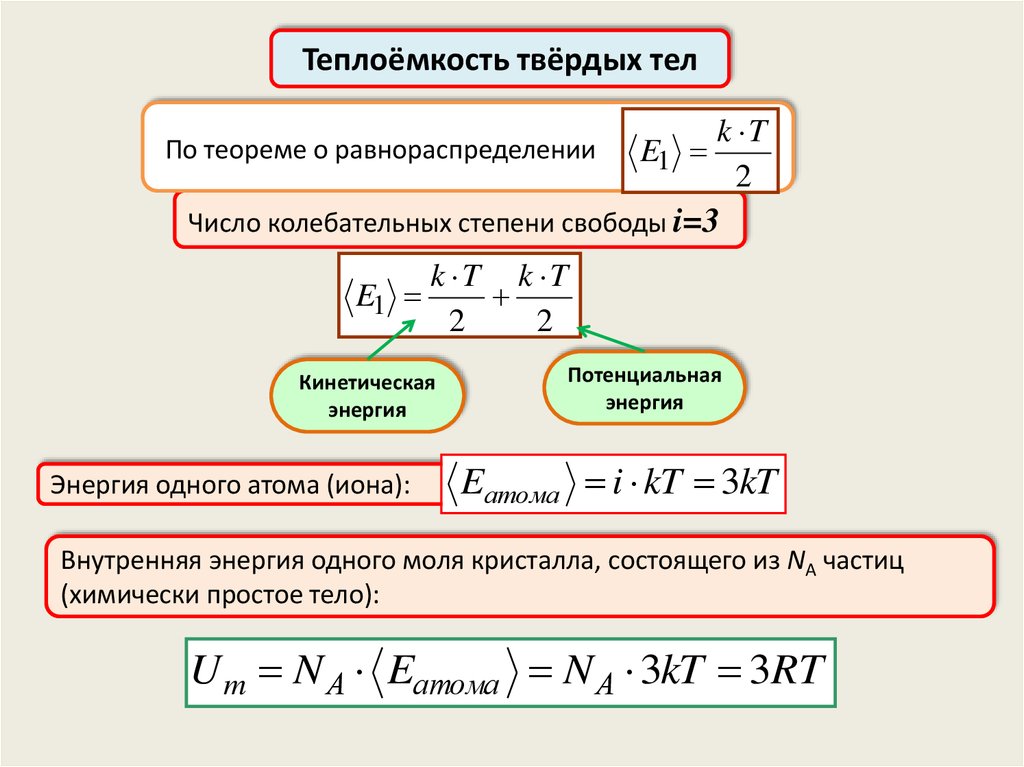
Теплоёмкость твёрдых тел
По теореме о равнораспределении
E1
k T
2
Число колебательных степени свободы i=3
E1
k T k T
2
2
Кинетическая
энергия
Энергия одного атома (иона):
Потенциальная
энергия
Eатома i kT 3kT
Внутренняя энергия одного моля кристалла, состоящего из NА частиц
(химически простое тело):
U m N А Eатома N А 3kT 3RT

58.

Теплоёмкость твёрдых тел. Закон Дюлонга и Пти
U m 3RT
Молярная теплоёмкость:
dU m
CV
3R
dT
Молярная теплоёмкость всех химически простых тел одинакова, не
зависит от температуры и равна:
Дж
CV 3R 25
Это – закон Дюлонга и Пти:
моль К
Для химических соединений число частиц в одном моле вещества в z раз
больше (z – число атомов в молекуле)
Пример: в моле NaCl содержится NА атомов натрия и NА атомов хлора; z =2
CV 3Rz

59.

Теплоёмкость твёрдых тел. Закон Дюлонга и Пти
Эксперимент:
Классическая статистика не годится;
нужно использовать квантовые статистики