Similar presentations:
Графические информационные модели
1. Графические информационные модели
2.
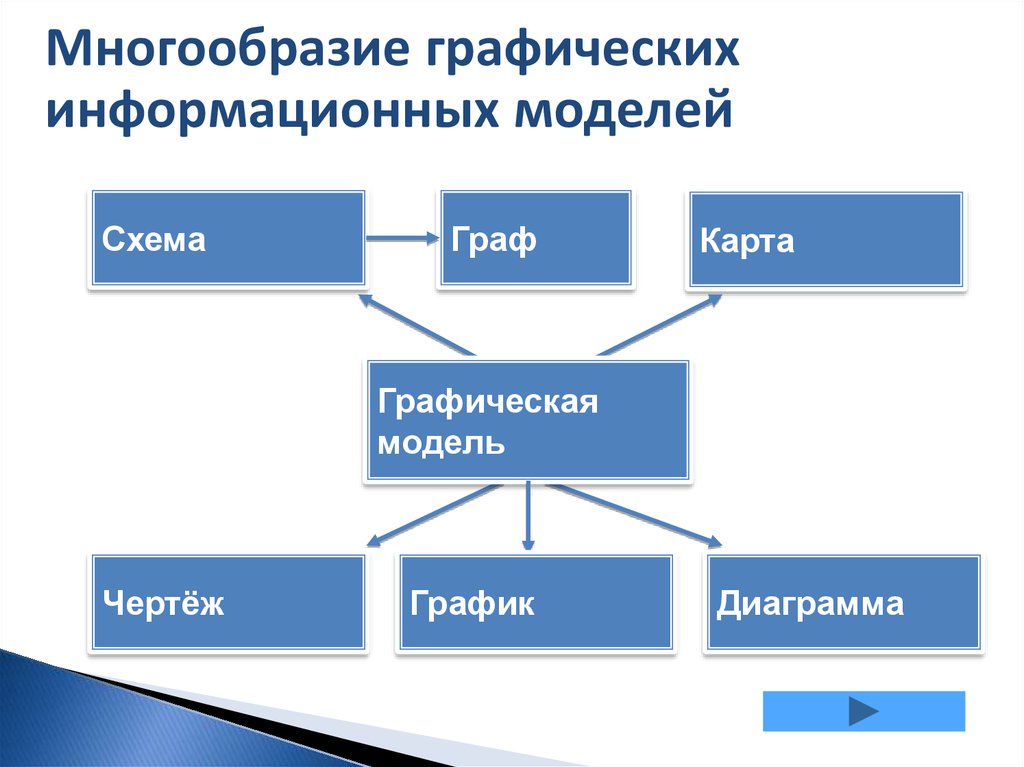
Многообразие графическихинформационных моделей
Схема
Граф
Карта
Графическая
модель
Чертёж
График
Диаграмма
3.
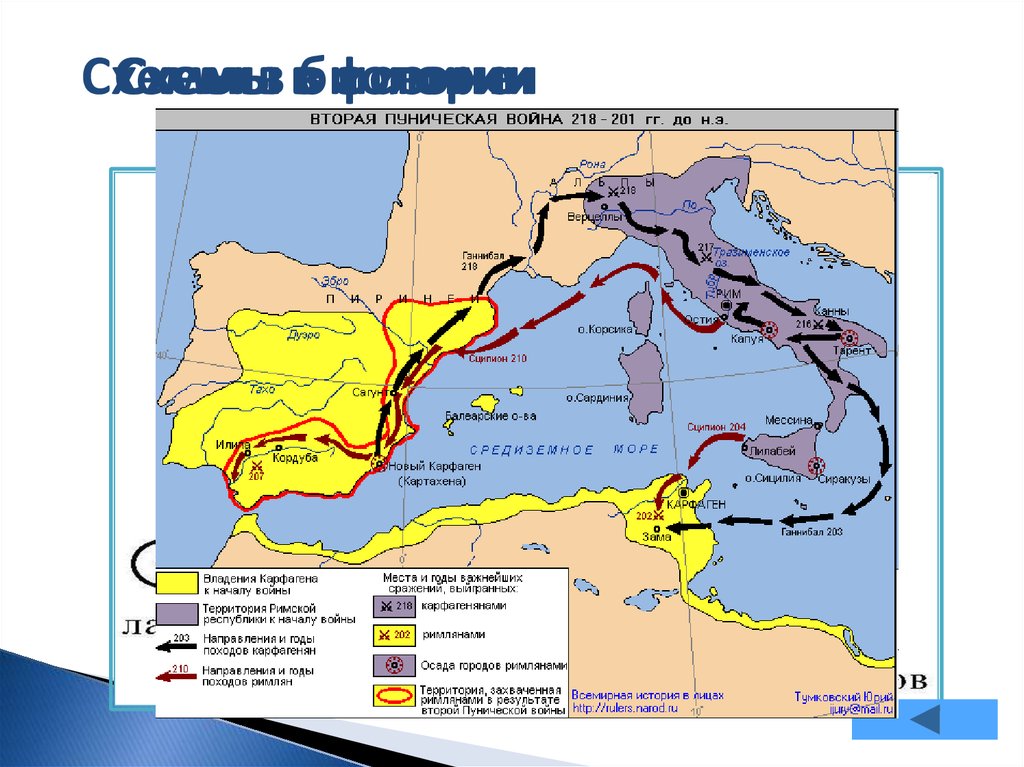
СхемыСхемыв ввбиологии
физике
истории
Р
геноти
п
гаметы
F1
♀
♂
4.
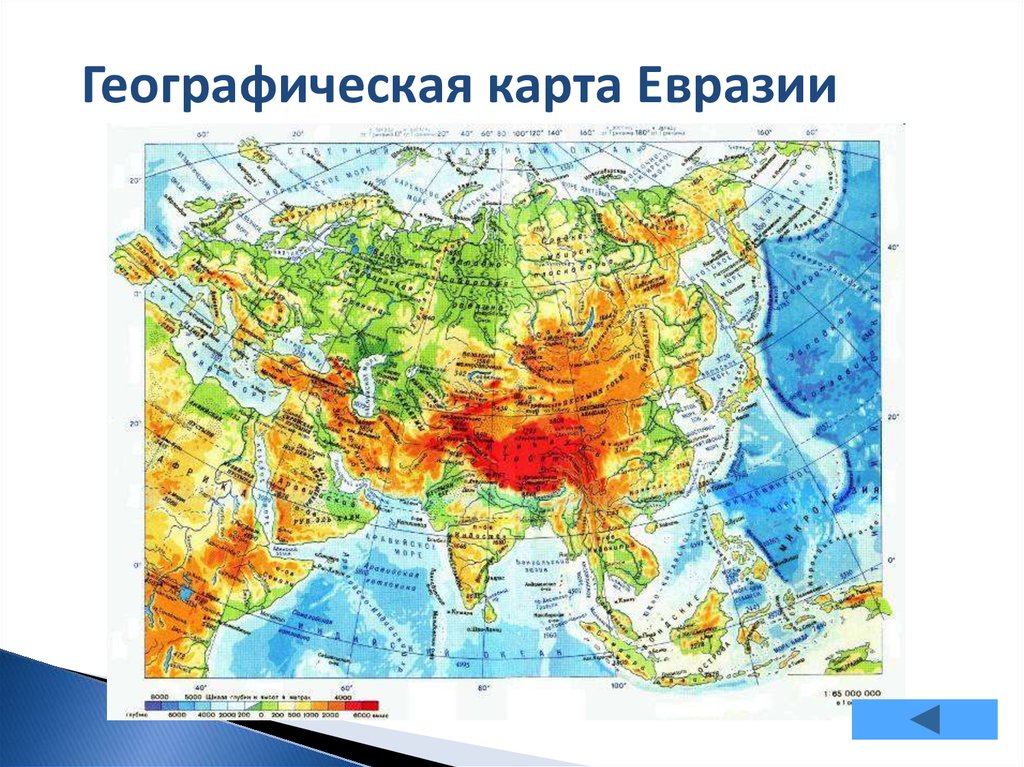
Географическая карта Евразии5.
Чертёж детали6.
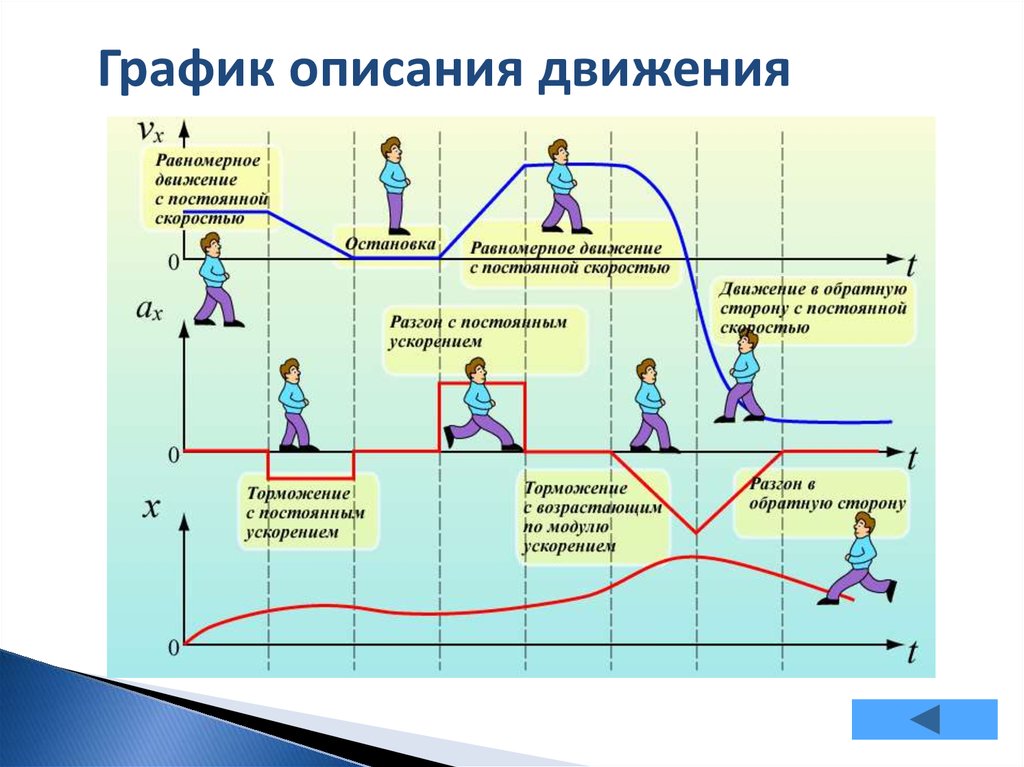
График описания движения7. Модели на графах
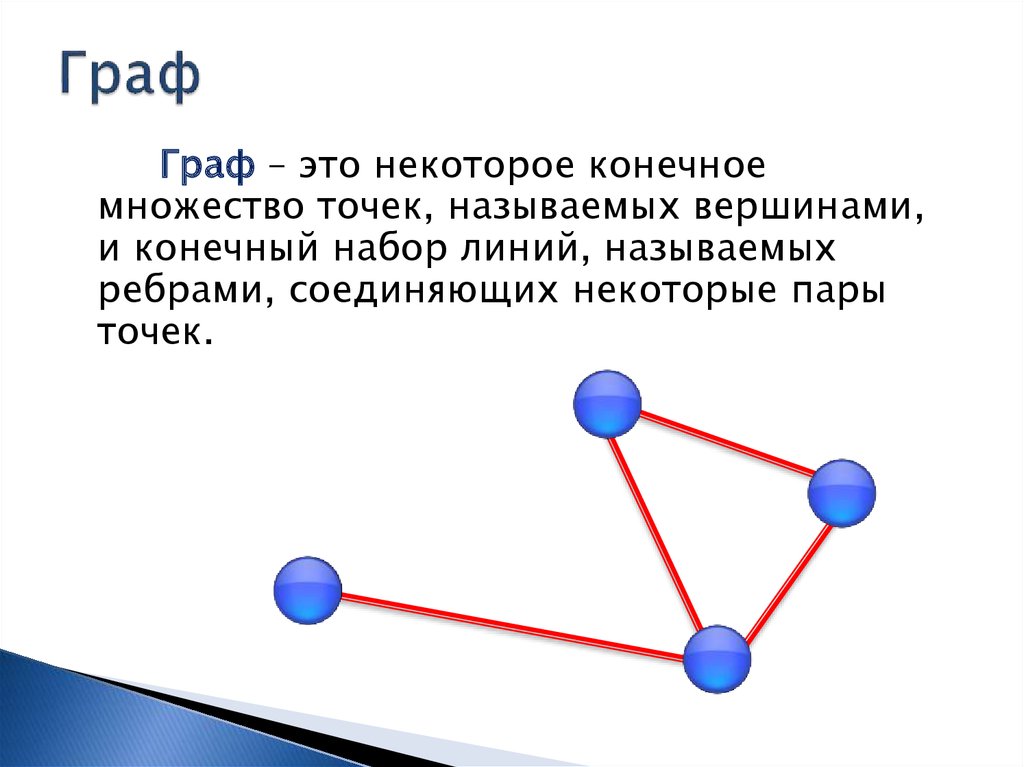
8. Граф
– это некоторое конечноемножество точек, называемых вершинами,
и конечный набор линий, называемых
ребрами, соединяющих некоторые пары
точек.
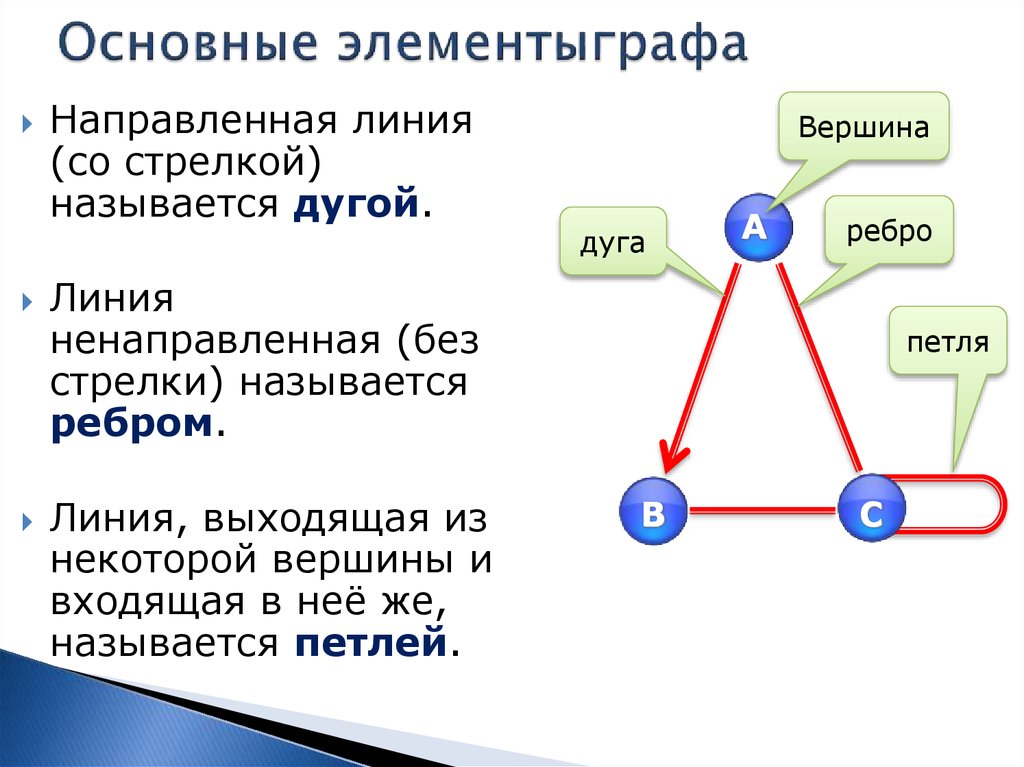
9. Основные элементыграфа
Направленная линия(со стрелкой)
называется дугой.
Вершина
дуга
А
ребро
Линия
ненаправленная (без
стрелки) называется
ребром.
Линия, выходящая из
некоторой вершины и
входящая в неё же,
называется петлей.
петля
В
С
10.
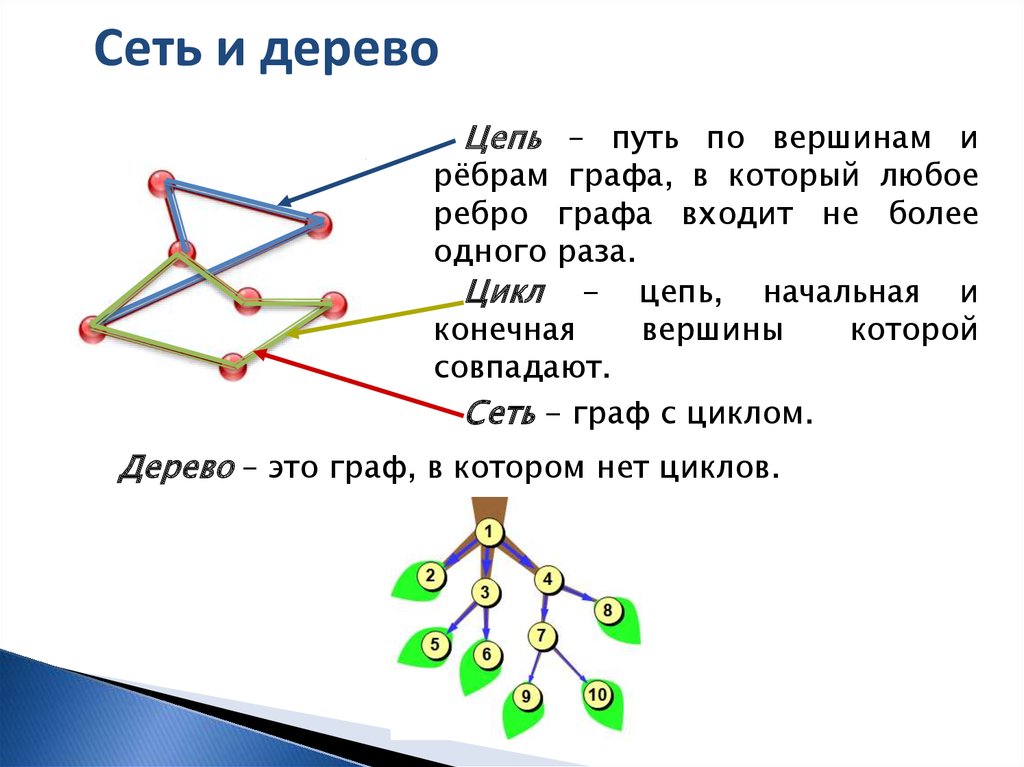
Сеть и деревоЦепь – путь по вершинам и
рёбрам графа, в который любое
ребро графа входит не более
одного раза.
Цикл - цепь, начальная и
конечная
вершины
которой
совпадают.
Сеть - граф с циклом.
Дерево – это граф, в котором нет циклов.
11. Немного истории
Первая работа по теорииграфов была написана еще в
1736 году Леонардом Эйлером.
(>>>)
Впервые понятие «граф»
ввел в 1936 году венгерский
математик Денеш Кёниг.
12. Задача
13.
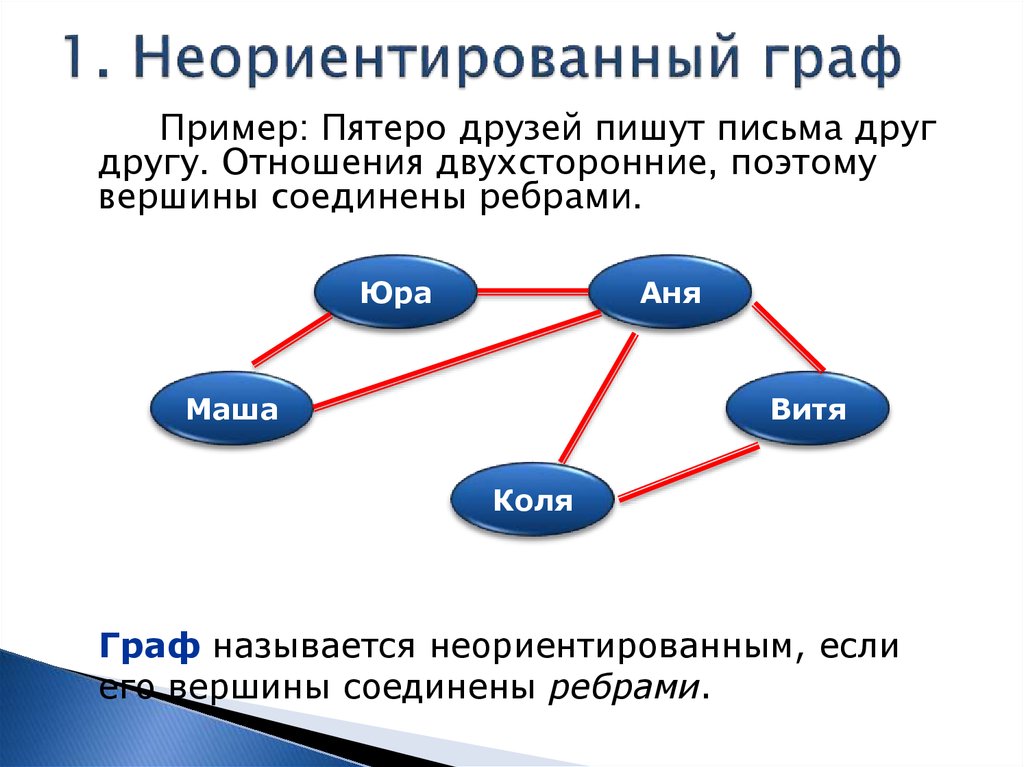
Пример: Пятеро друзей пишут письма другдругу. Отношения двухсторонние, поэтому
вершины соединены ребрами.
Юра
Аня
Маша
Витя
Коля
Граф называется неориентированным, если
его вершины соединены ребрами.
14.
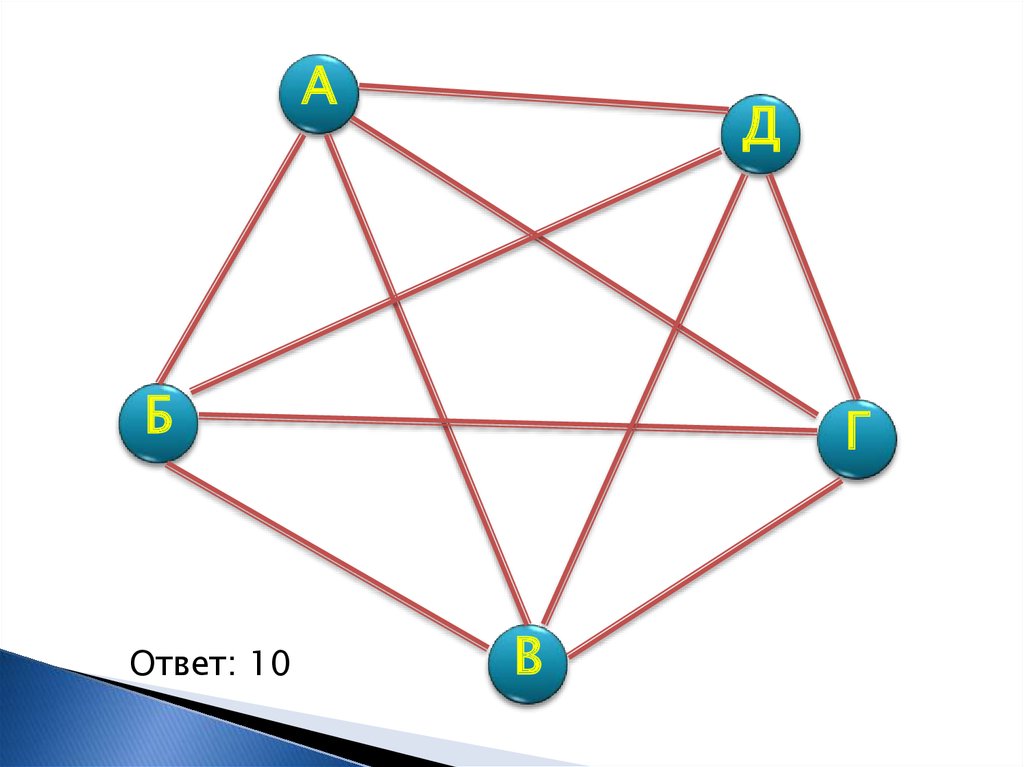
Аркадий, Борис, Владимир, Григорий иДмитрий при встрече обменялись
рукопожатиями (каждый пожал руку
каждому по одному разу). Сколько всего
рукопожатий было сделано?
15. Виды графов
АД
Б
Ответ: 10
Г
В
16. 1. Неориентированный граф
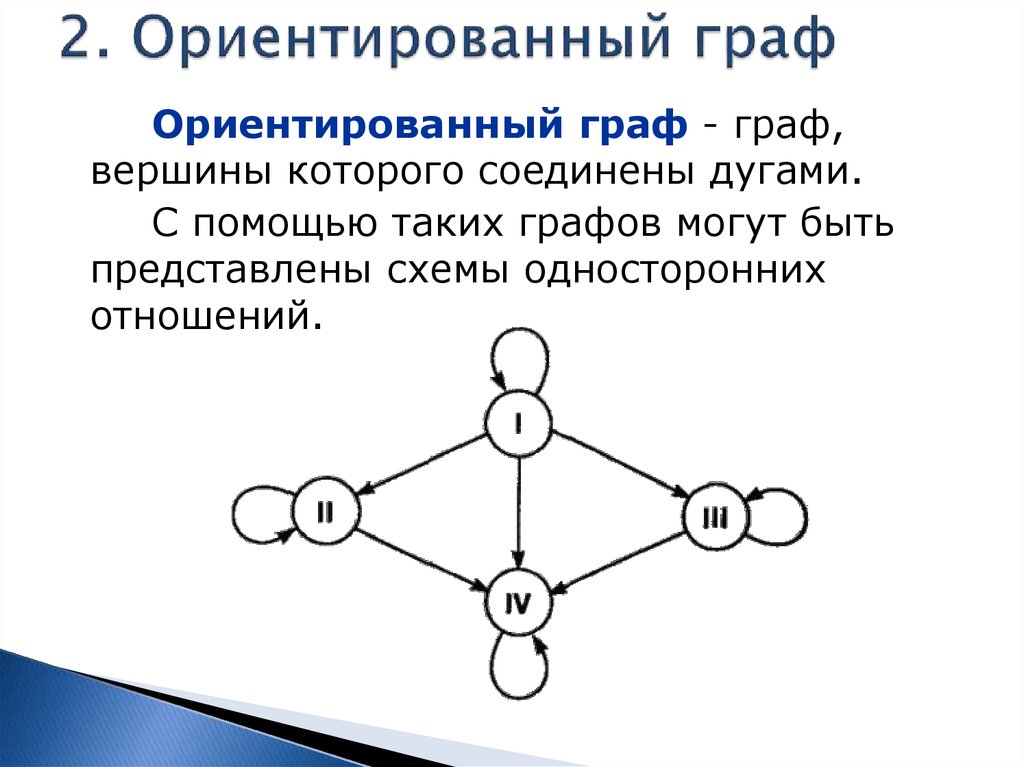
Ориентированный граф - граф,вершины которого соединены дугами.
С помощью таких графов могут быть
представлены схемы односторонних
отношений.
17. Задача 1
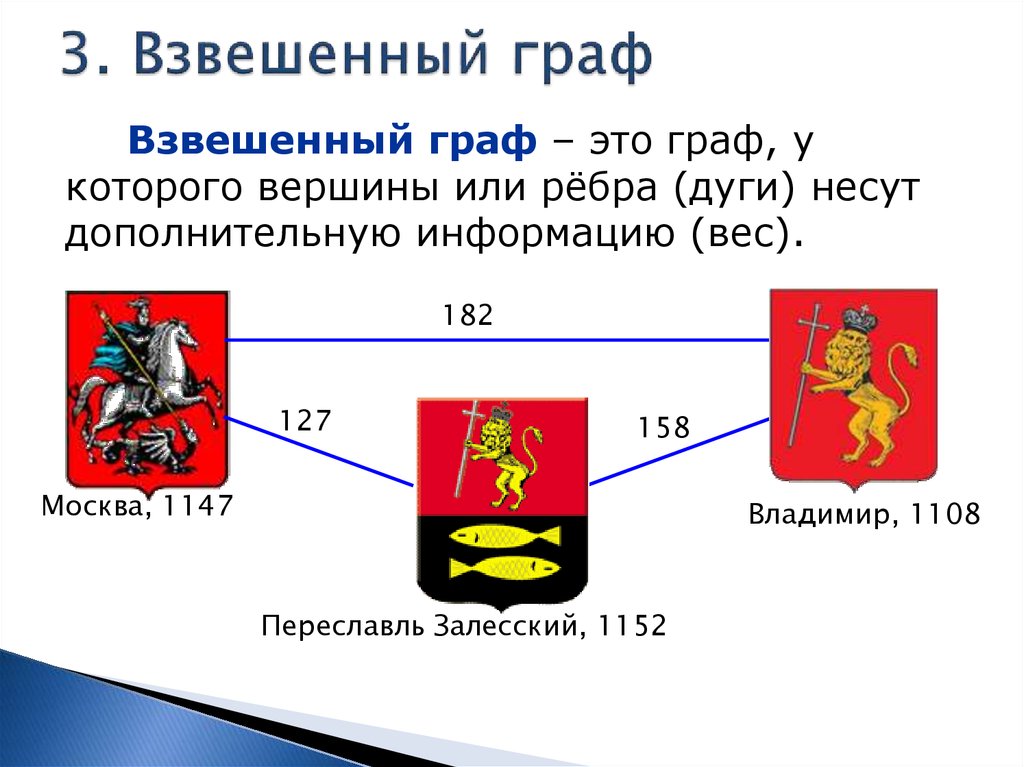
Взвешенный граф – это граф, укоторого вершины или рёбра (дуги) несут
дополнительную информацию (вес).
182
127
158
Москва, 1147
Владимир, 1108
Переславль Залесский, 1152
18.
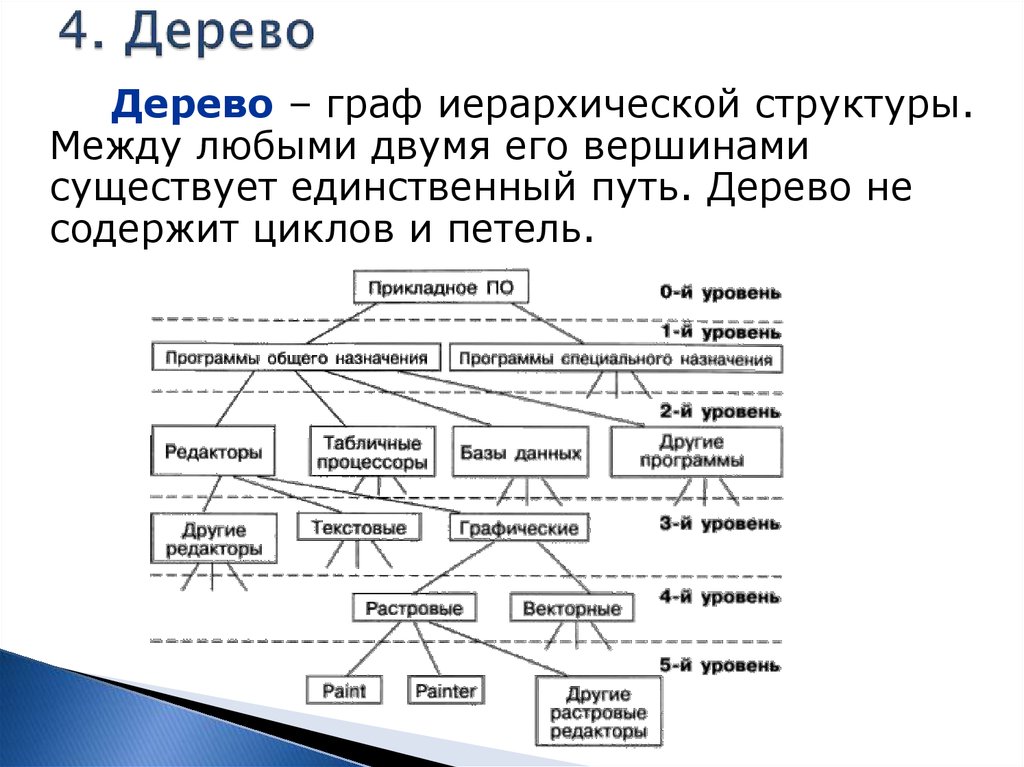
Дерево – граф иерархической структуры.Между любыми двумя его вершинами
существует единственный путь. Дерево не
содержит циклов и петель.
19. 2. Ориентированный граф
Укажите корневуювершину, объекты 1го, 2-го и 3-го уровней
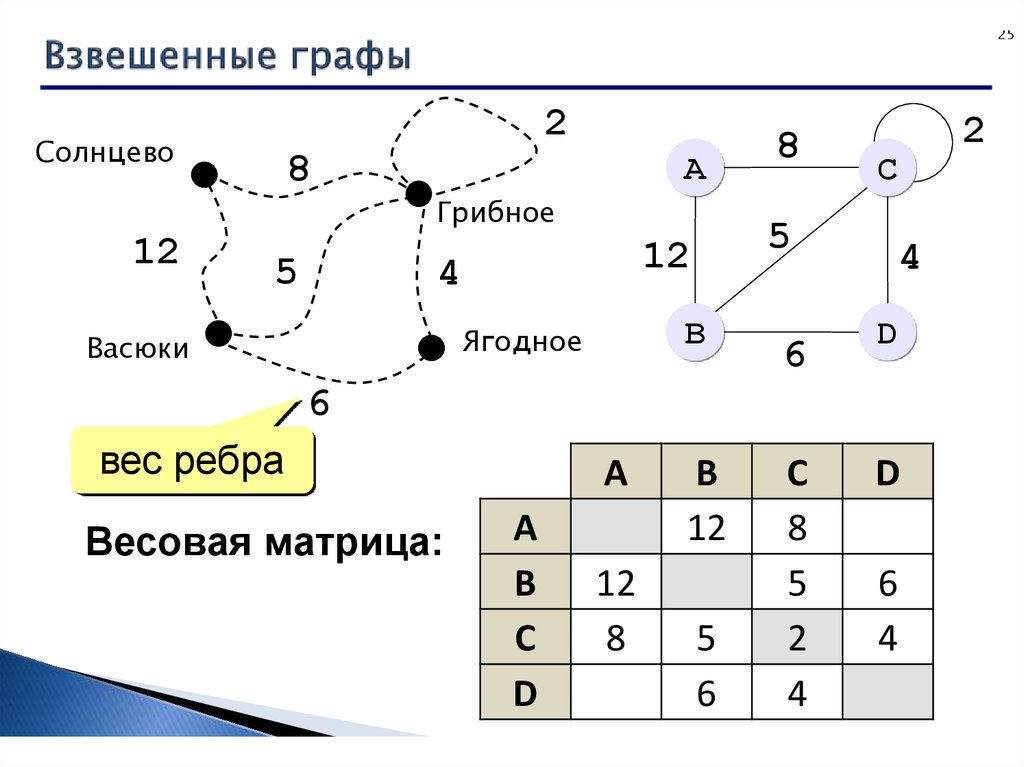
20. 3. Взвешенный граф
21. 4. Дерево
Информация и информационные процессы, 10 класс24
Матрица смежности
A
B
C
D
A
B
C
D
A
0
1
1
0
B
1
0
1
1
C
1
1
1
1
D
0
1
1
0
петля
К.Ю. Поляков, Е.А. Ерёмин, 2013-2014
http://kpolyakov.spb.ru
22.
Информация и информационные процессы, 10 класс25
2
Солнцево
8
A
Грибное
12
5
B
Ягодное
Васюки
2
C
5
12
4
8
6
4
D
6
вес ребра
Весовая матрица:
К.Ю. Поляков, Е.А. Ерёмин, 2013-2014
A
A
B
C
D
12
8
B
12
5
6
C
8
5
2
4
D
6
4
http://kpolyakov.spb.ru
23. Способы описания графов
Информация и информационные процессы, 10 классВ
A
С
E
К.Ю. Поляков, Е.А. Ерёмин, 2013-2014
D
http://kpolyakov.spb.ru
24. Матрица и список смежности
Информация и информационные процессы, 10 класс14
В
A
25
10
E
С
7
D
3
К.Ю. Поляков, Е.А. Ерёмин, 2013-2014
http://kpolyakov.spb.ru
25. Взвешенные графы
Информация и информационные процессы, 10 классA
A
B
C
D
Е
0
1
1
0
К.Ю. Поляков, Е.А. Ерёмин, 2013-2014
B
0
1
0
1
C
1
1
0
1
D
1
0
0
Е
0
1
1
0
0
http://kpolyakov.spb.ru
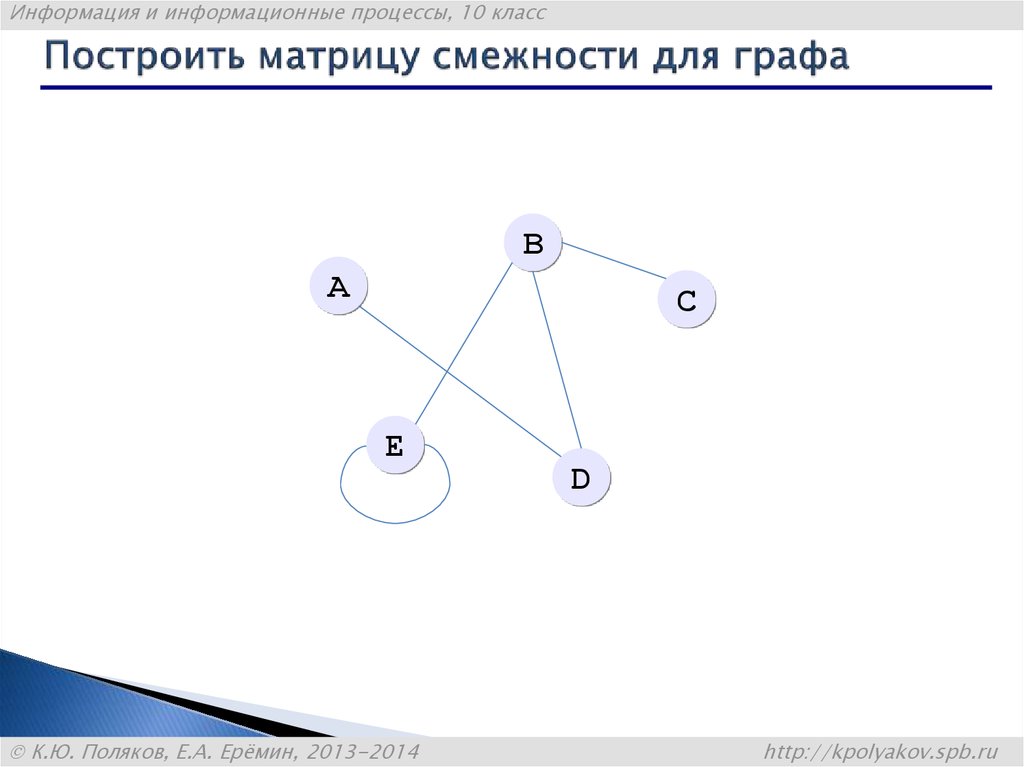
26. Построить матрицу смежности для графа
27. Построить весовую матрицу для графа
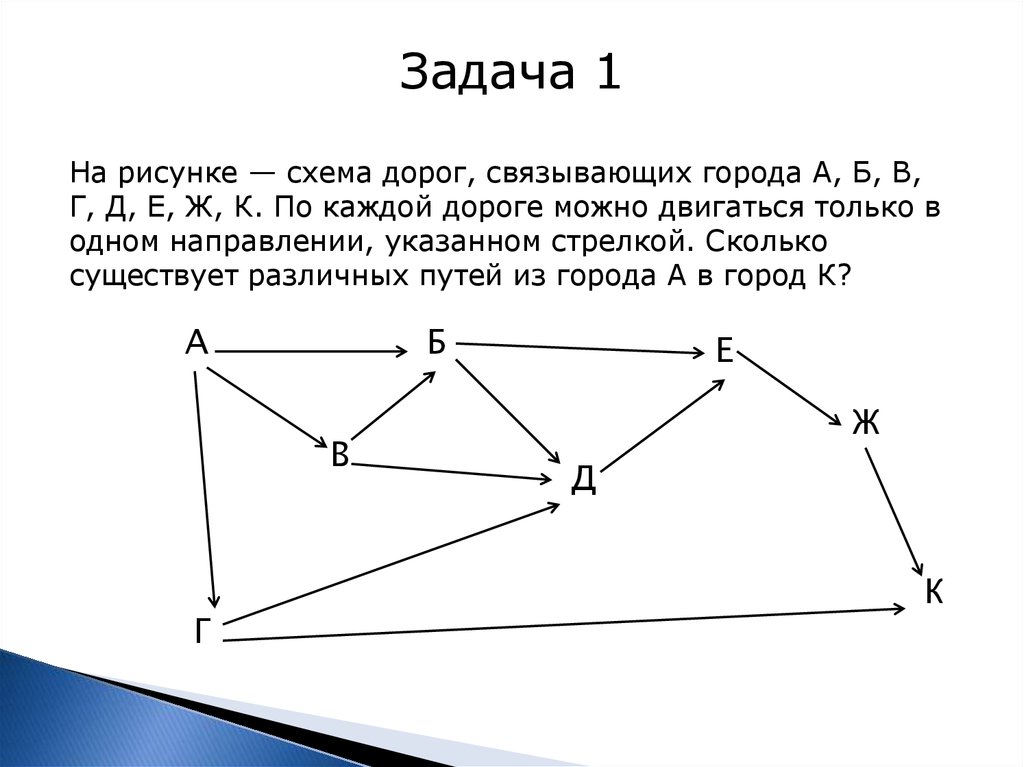
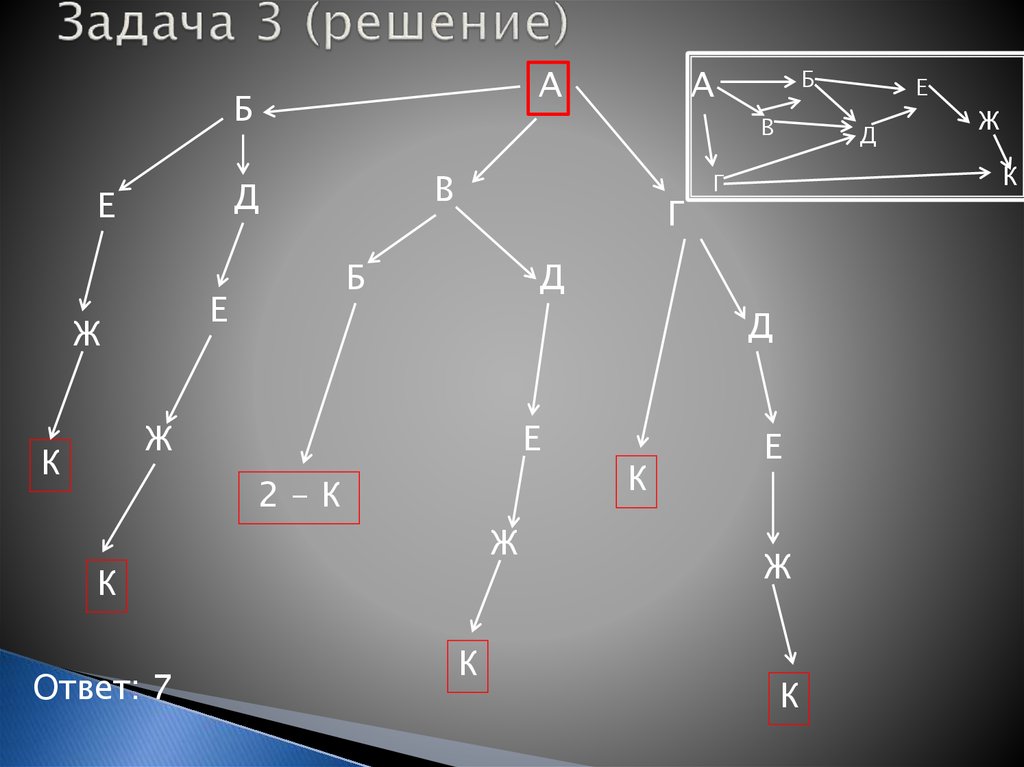
Задача 1На рисунке — схема дорог, связывающих города А, Б, В,
Г, Д, Е, Ж, К. По каждой дороге можно двигаться только в
одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город К?
А
Б
В
Г
Е
Ж
Д
К
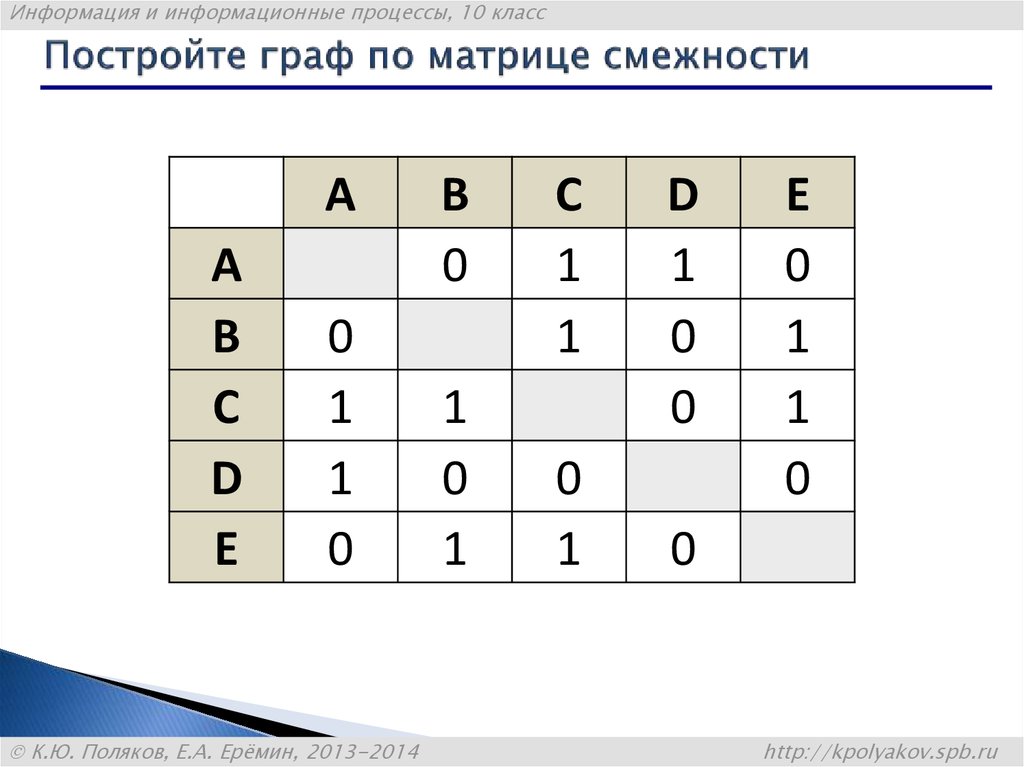
28. Постройте граф по матрице смежности
АБ
В
Г
Б
Е
Ж
2-К
Ж
К
Ответ: 7
К
К
Ж
К
Г
Д
Е
Е
Д
Д
Ж
К
Б
В
Д
Е
А
Е
Ж
К
29. Решение задач с помощью графов
30.
АF
4
5
В
6
6
E
4
С
3
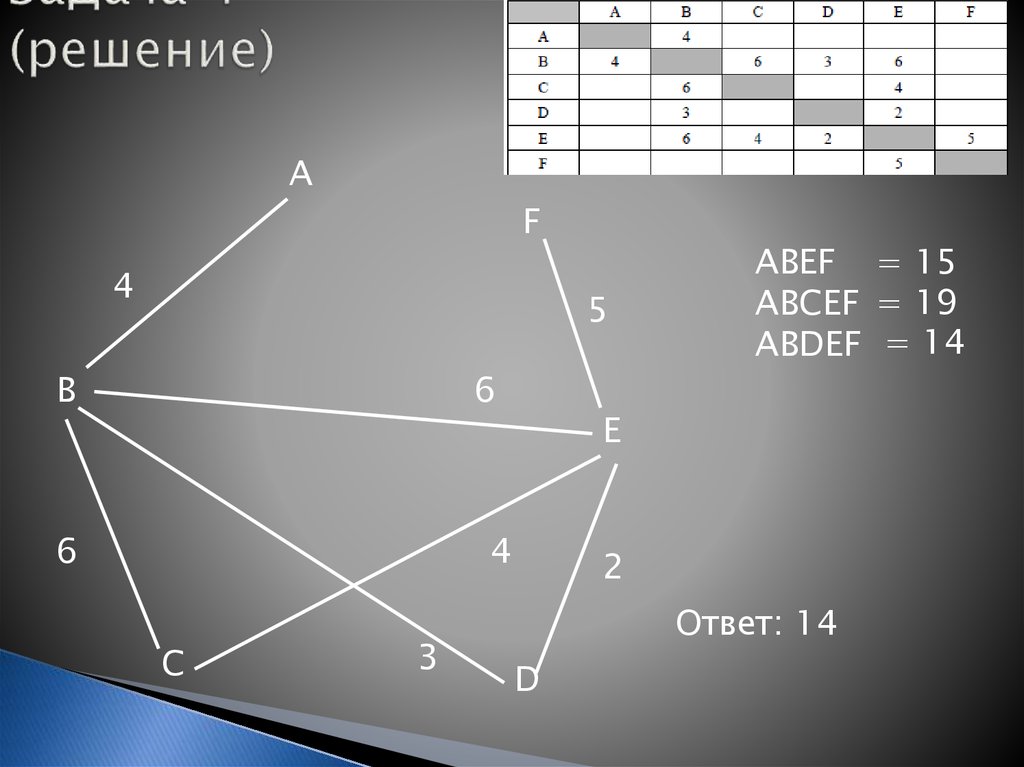
ABEF = 15
ABCEF = 19
ABDEF = 14
2
Ответ: 14
D
31. Задача 3 (решение)
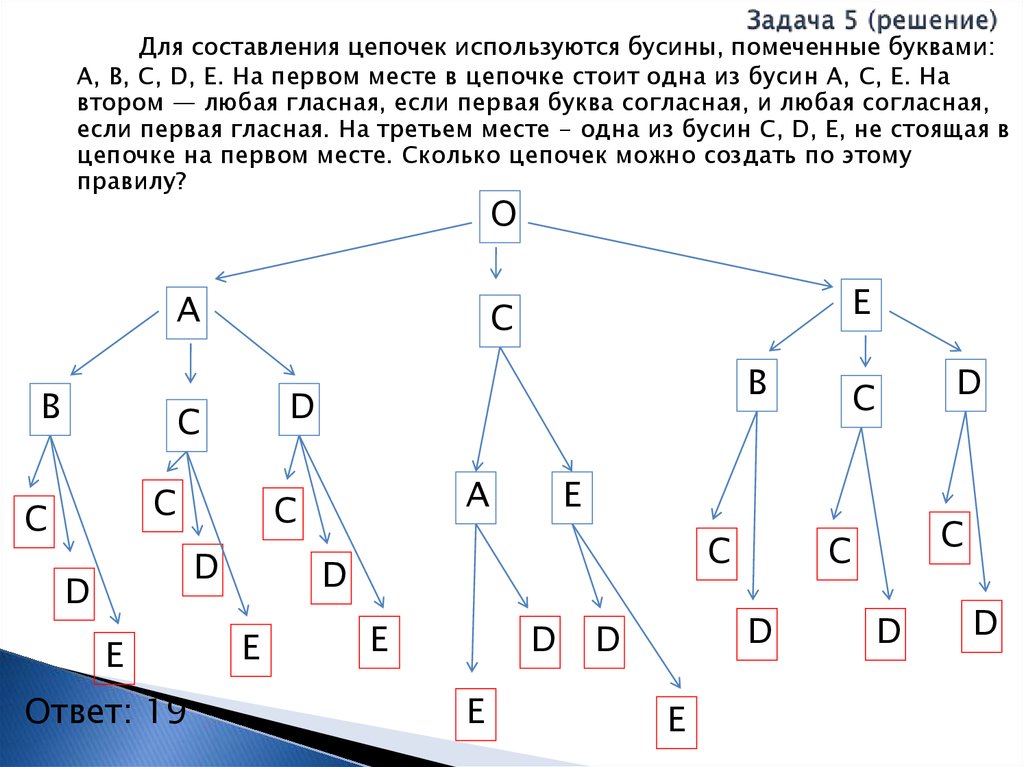
Для составления цепочек используютсябусины, помеченные буквами: А, В, С, D, Е.
На первом месте в цепочке стоит одна из
бусин А, С, Е. На втором — любая гласная,
если первая буква согласная, и любая
согласная, если первая гласная. На третьем
месте - одна из бусин С, D, Е, не стоящая в
цепочке на первом месте. Сколько цепочек
можно создать по этому правилу?
32. Задача 2
Для составления цепочек используются бусины, помеченные буквами:А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На
втором — любая гласная, если первая буква согласная, и любая согласная,
если первая гласная. На третьем месте - одна из бусин С, D, Е, не стоящая в
цепочке на первом месте. Сколько цепочек можно создать по этому
правилу?
О
А
B
C
E
Ответ: 19
А
C
D
D
B
D
C
C
E
C
E
C
D
E
E
D
E
D
C
D
D
E
C
C
D
D
















 informatics
informatics








