Similar presentations:
Сокращенные таблицы истинности
1. Сокращенные таблицы истинности
Значение сложного высказывания определяется (в некоторых случаях)значением только одного из составляющих.
Например, суждение «Волга является одной из самых протяженных
рек в России и впадает в Балтийское море» - ложно, и для того,
чтобы это показать, достаточно ложности высказывания «Волга
впадает в Балтийское море»
Поскольку конъюнкция двух высказываний истинна е.т.е. истинны эти
высказывания одновременно,
конъюнкция двух высказываний ложна, если известно, что одно из этих
высказываний ложно, и значение другого высказывания этот результат не
изменит.
2. Сокращенные таблицы истинности
КонъюнкцияИмпликация
( Ложь) = (Ложь ) = Ложь
( Ложь) =
(Ложь ) = Ист.
( Ист.) = (Ист. ) =
( Ист.) = Ист.
(Ист. ) =
Стрелка Пирса
Нестрогая дизъюнкция
( Ложь) = (Ложь ) =
( Ложь) = (Ложь ) =
( Ист.) = (Ист. ) = Ист.
( Ист.) = (Ист. ) = Ложь
Эквиваленция
( Ложь) = (Ложь ) =
( Ист.) = (Ист. ) =
Строгая дизъюнкция
(
Ложь) = (Ложь
) =
(
Ист.) = (Ист.
) =
Штрих Шеффера
( Ложь) = (Ложь ) = Ист.
( Ист.) = (Ист. ) =
3.
Сокращенные таблицы истинностиРассмотрим пример:
(((а b) c) a), при а = «Ист.»
Подставим значения
(((Ист. b) c) Ист.)
Ист.)
Подберем соответствующее(
правило
= Ист.,
независимо от значения и сложности « »
Таким образом,
(((а b) c) a) = «Ист.», при а = «Ист.»
4.
Сокращенные таблицы истинностиаях необходимо применить несколько правил. Например …
(((а b) (c a)), при а = «Ист.»
Подставим значения
(((Ист. b) (c Ист.))
(Ист. ) = Ист.
Подберем соответствующие правила
( Ист.) = Ист.
Промежуточный результат:
(Ист. Ист.)
Подберем еще одно правило
( Ист.) = (Ист. ) = Ложь
Таким образом, (((а
b) (c a)) = «Ложь», при а = «Ист.»
5.
Сокращенные таблицы истинностиВ некоторых случаях исходная формула лишь упрощается, но значение
определить не удается.
Например …
((а ( b с)) a), при а = «Ложь»
Подставим значения
((Ложь ( b c)) Ложь))
(Ложь ) =
Подберем соответствующее правило
Промежуточный результат:
(( b c) Ложь)
Подберем еще одно правило
Таким образом,((а
( Ложь) =
( b с)) a) = ( b c) , при а = «Ложь»
6.
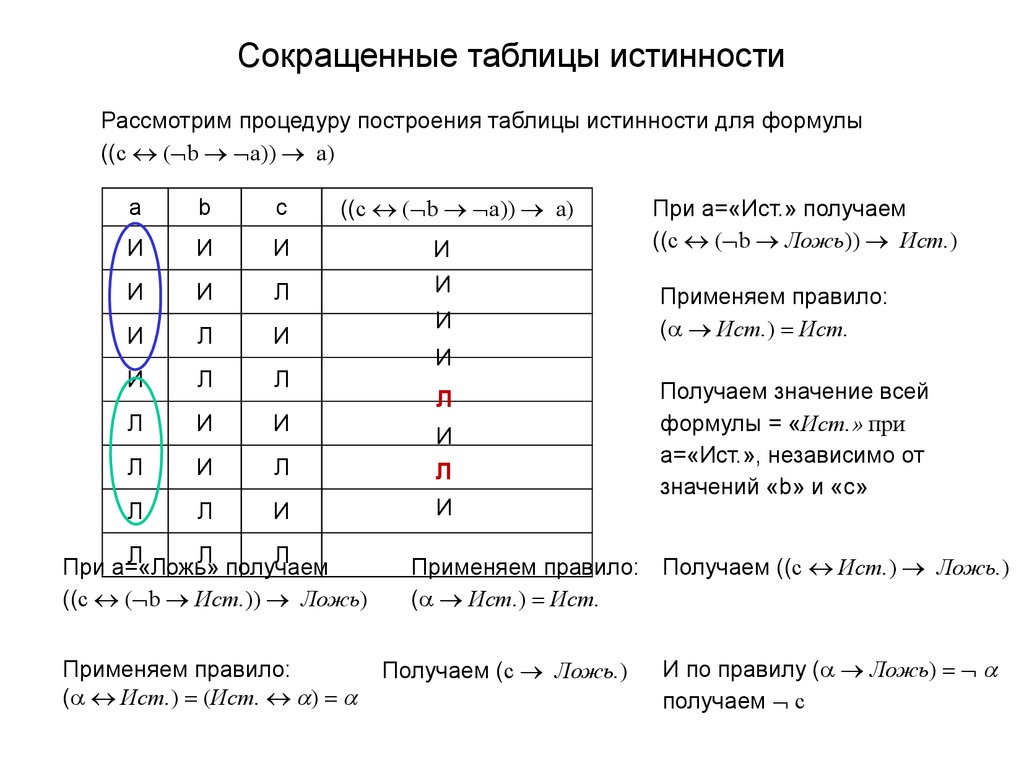
Сокращенные таблицы истинностиРассмотрим процедуру построения таблицы истинности для формулы
((c ( b a)) a)
((c ( b a)) a)
a
b
c
И
И
И
И
И
И
Л
И
И
Л
И
И
Л
Л
Л
И
И
Л
И
Л
Л
Л
Л
И
И
Л
Л
Л
При а=«Ложь» получаем
((c ( b Ист.)) Ложь)
Применяем правило:
( Ист.) = (Ист. ) =
И
При а=«Ист.» получаем
((c ( b Ложь)) Ист.)
Применяем правило:
( Ист.) = Ист.
И
Л
И
Получаем значение всей
формулы = «Ист.» при
а=«Ист.», независимо от
значений «b» и «с»
Применяем правило: Получаем ((c Ист.) Ложь.)
( Ист.) = Ист.
Получаем (c Ложь.)
И по правилу ( Ложь) =
получаем c
7.
Задания к тесту2) Примените метод сокращённых таблиц.
Формула ((а b) c), при b = «Ист.» равна:
A. ( b c)
B. «Ист.»
C. «Ложь»
D. (b c)
1) Примените метод сокращённых таблиц.
Формула ((а b) c), при b = «Ист.» равна:
A. с
B. «Ист.»
C. «Ложь»
D. а
3) Примените метод сокращённых таблиц.
Формула ((b (a c)) (d b)), при b = «Ложь»
равна:
4) Примените метод сокращённых таблиц.
A. с
Формула (((b a) (b c)) b), при b = «Ист.»
B. «Ист.»
равна:
C. «Ложь»
A. с
D. а
B. «Ист.»
E. (a c)
C. «Ложь»
F. ((a c) d)
D. (а c)
E. (а c)






 mathematics
mathematics philosophy
philosophy








