Основные этапы развития комбинаторики как науки

1.

4 9 2
3 5 7
8 1 6
Основные этапы развития
комбинаторики как науки

2. 1 этап: задачи и головоломки в Древнем мире

3. задачи и головоломки в Древнем мире

Задачи и головоломки, связанные с
перебором возможных вариантов,
комбинаций и перестановок предметов и в
дальнейшем получившие название
«комбинаторных» интересовали людей
ещё в древности.

4. Комбинаторика в Древнем Китае

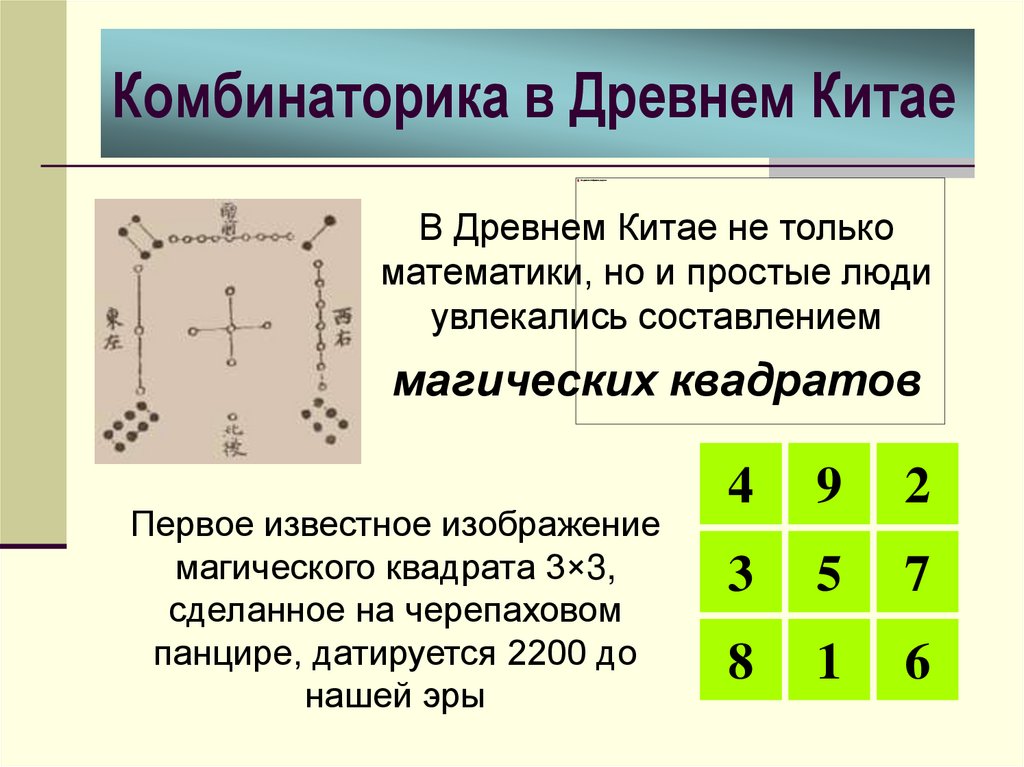
В Древнем Китае не только
математики, но и простые люди
увлекались составлением
магических квадратов
Первое известное изображение
магического квадрата 3×3,
сделанное на черепаховом
панцире, датируется 2200 до
нашей эры
4
9
2
3
5
7
8
1
6

5. Комбинаторика в Древней Греции

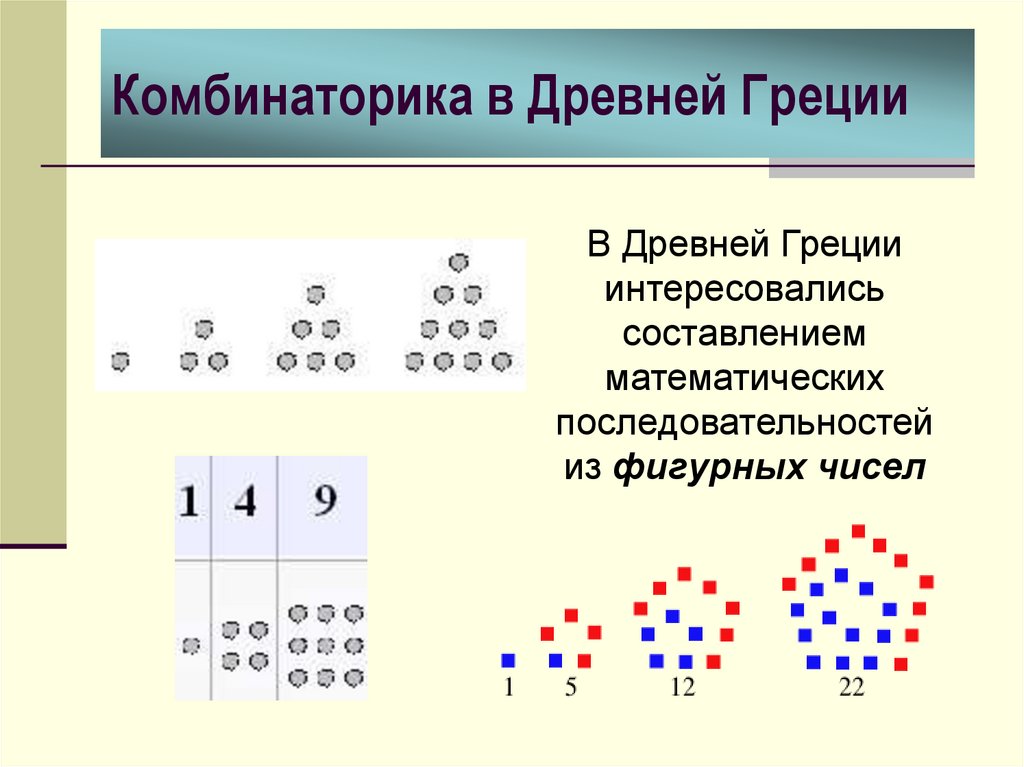
В Древней Греции
интересовались
составлением
математических
последовательностей
из фигурных чисел

6. Комбинаторика в счётно-логических играх

В разных странах изучались комбинаторные задачи
и приёмы, связанные со счётно-логическими играми
В играх в кости, нарды, карты, шашки, шахматы
требовались умения рассчитывать, составлять
планы и опровергать планы противника.
О таких играх английский поэт Уордсворт писал:
Не нужно нам владеть клинком,
Не ищем славы громкой.
Тот побеждает, кто знаком
С искусством мыслить, тонким.

7. Пример применения комбинаторики в шахматах

На краю доски у коня
4 возможных хода
В центре доски у коня
8 возможных ходов
Вывод : в центре доски конь расположен лучше!

8. 2 этап: первые научные обобщения в средние века

9. первые научные обобщения

Кардано - изобретатель
шифровального
устройства, получившего
название «решётка
Кардано».
Джероламо Кардано
(1501—1576)
После его смерти было
опубликовано его
математическое
исследование по теории
азартных игр

10. первые научные обобщения

Свои оригинальные
исследования по
арифметике, алгебре и
геометрии Тарталья
издал в книге «Общий
трактат о числе и мере»
среди которых были и
исследования по
теории комбинаторики
Никколо Тарталья
(1500-1557)

11. первые научные обобщения

Итальянский физик и
астроном Галилей
впервые использовал
комбинаторные идеи в
прикладных исследованиях
по теории механики,
баллистики и при изучении
отдельных вопросов
астрономии
Галилео Галилей
(1564-1642)

12. первые научные обобщения

Придумал машину, способную
складывать и вычитать,
названную впоследствии
«Паскалево колесо».
Блез Паскаль
(1623-1662)
Занимался решением
комбинаторных задач в
рамках новой для того
времени науки – теории
вероятностей

13. первые научные обобщения

Знаменитый французский
математик Ферма в своих
исследованиях теории чисел
и теории вероятностей
заложил
теоретические основы
решения
комбинаторных задач
Пьер Ферма
(1601-1665)

14. 3 этап: выделение комбинаторики как самостоятельной науки

15. выделение комбинаторики как самостоятельной науки

В своей работе «Об искусстве
комбинаторики» (1666г.)
впервые стал рассматривать
комбинаторику как отдельный
раздел математики
Ввёл термин «комбинаторика»
Готфрид Лейбниц
(1646-1716)

16. выделение комбинаторики как самостоятельной науки

Его считают одним из
величайших математиков
всех времен и народов
«Мимоходом» (занимаясь в
основном математическим
анализом и алгеброй) он
внёс значительный вклад
и в теорию комбинаторики
Леонард Эйлер
(1707-1783)

17. 4 этап: комбинаторика в современном обществе

18. комбинаторика и компьютер

Новый толчок в исследованиях
комбинаторики связан с развитием
электронно-вычислительной
техники
Комбинаторные идеи
получили широкое
использование в
программировании

19. комбинаторика и компьютер

С другой стороны с помощью
современных компьютеров
удалось решить ряд трудных
комбинаторных задач
Задача о четырёх
красках
С помощью компьютера окончательно доказали, что любую карту
можно раскрасить в 4 цвета таким образом, что никакие две страны,
имеющие общую границу, не будут окрашены в один цвет.

20.

Спасибо
за
внимание!