Проводник в электроститческом поле. Электроемксоть. Энергия

1. ЭЛЕКТРОСТАТИКА

ПРОВОДНИК В
ЭЛЕКТРОСТИТЧЕСКОМ ПОЛЕ.
ЭЛЕКТРОЕМКСОТЬ. ЭНЕРГИЯ

2.

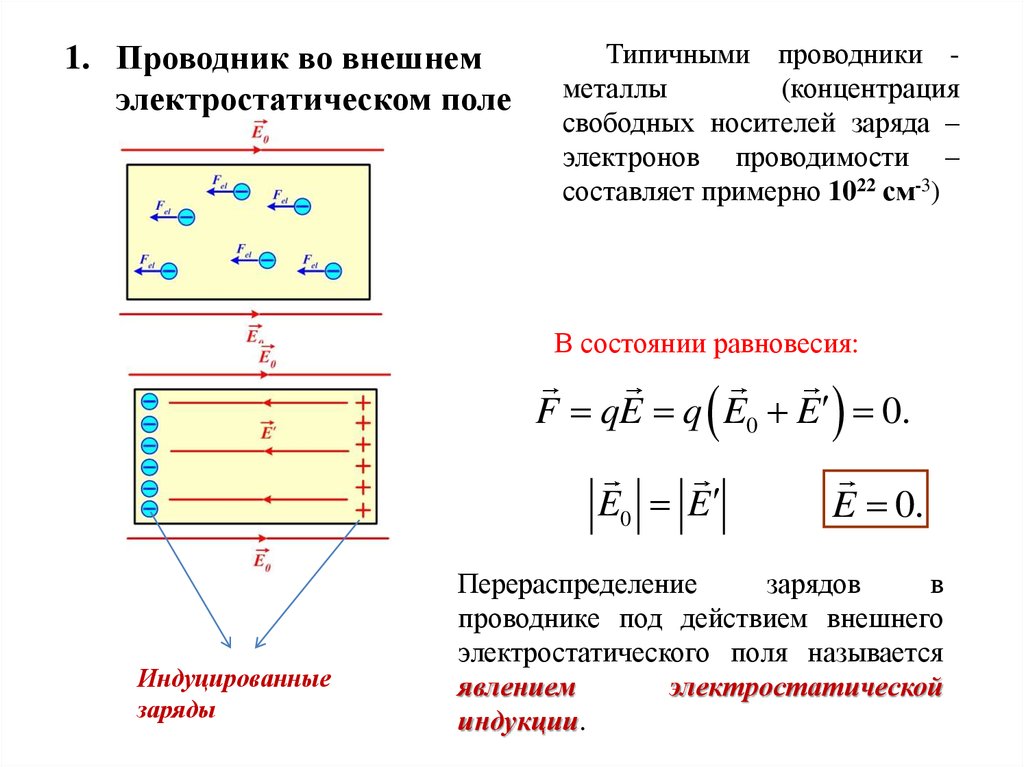
1. Проводник во внешнем
электростатическом поле
Типичными проводники металлы
(концентрация
свободных носителей заряда –
электронов проводимости –
составляет примерно 1022 см-3)
В состоянии равновесия:
F qE q E0 E 0.
E0 E
Индуцированные
заряды
E 0.
Перераспределение
зарядов
в
проводнике под действием внешнего
электростатического поля называется
явлением
электростатической
индукции.

3.

Индуцированные заряды располагаются на поверхности проводника. Они
исчезают после удаления проводника из электростатического поля.
Так можно получить два
заряженных
тела,
с
одинаковыми по величине,
но противоположными по
знаку зарядами.
Принцип электростатической
защиты (экранирование)

4.

Во всех точках внутри проводника напряженность
Согласно теореме Гаусса
q
E 0,
q dV ,
0.
V
q 0,
Внутри проводника
E 0.
E grad ,
1
равна нулю.
E dS 0
0 S
Вывод: внутри проводника объемная
плотность свободного заряда равна
нулю, а сам заряд располагается на его
поверхности.
const.
Поверхность проводника является эквипотенциальной поверхностью и
весь объем проводника представляет собой эквипотенциальную
область

5.

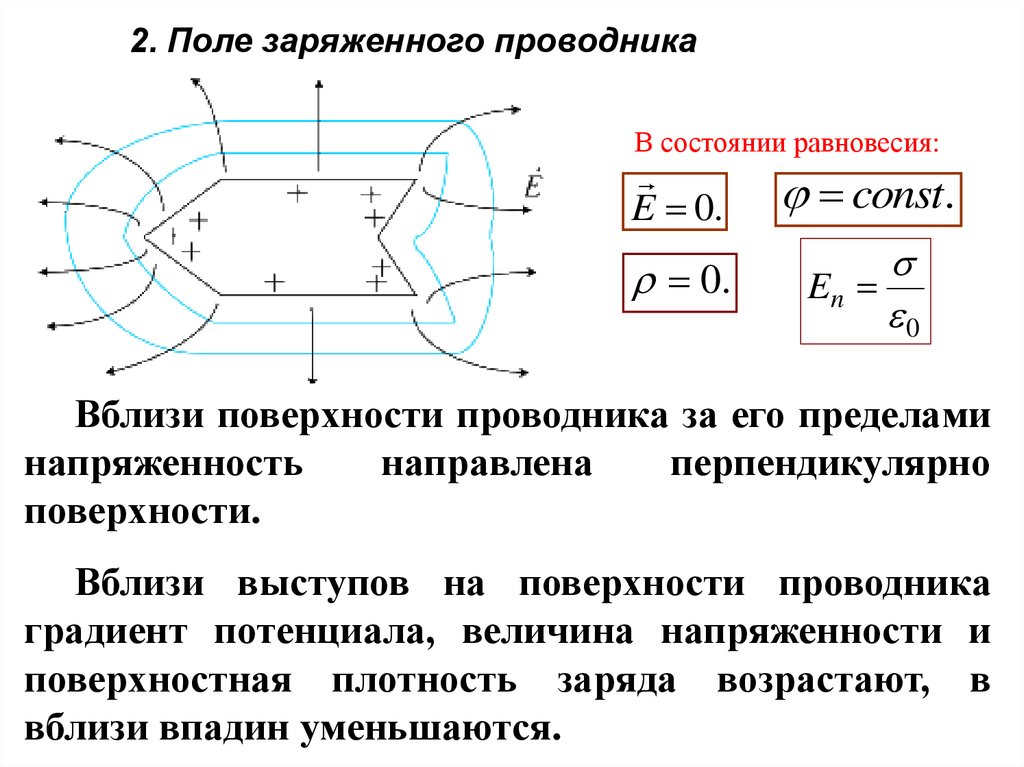
2. Поле заряженного проводника
В состоянии равновесия:
E 0.
const.
0.
En
0
Вблизи поверхности проводника за его пределами
напряженность
направлена
перпендикулярно
поверхности.
Вблизи выступов на поверхности проводника
градиент потенциала, величина напряженности и
поверхностная плотность заряда возрастают, в
вблизи впадин уменьшаются.

6.

3. Электрическая емкость
C 1q
C
- электрическая емкость проводника
C Ф фарада
Емкость уединенного проводника зависит от его формы, размеров
и диэлектрических свойств среды, в которой находится проводник, а также
электрических свойств, расположения, форм и размеров окружающих тел.
Практический интерес представляет система проводников,
электростатическое поле которых полностью сосредоточено
в объеме, занимаемом этой системой конденсатор!
q C ( 1 2 ) CU
- заряд на одной из обкладок конденсатора
U – разность потенциалов двух обкладок (для конденсатора напряжению)

7.

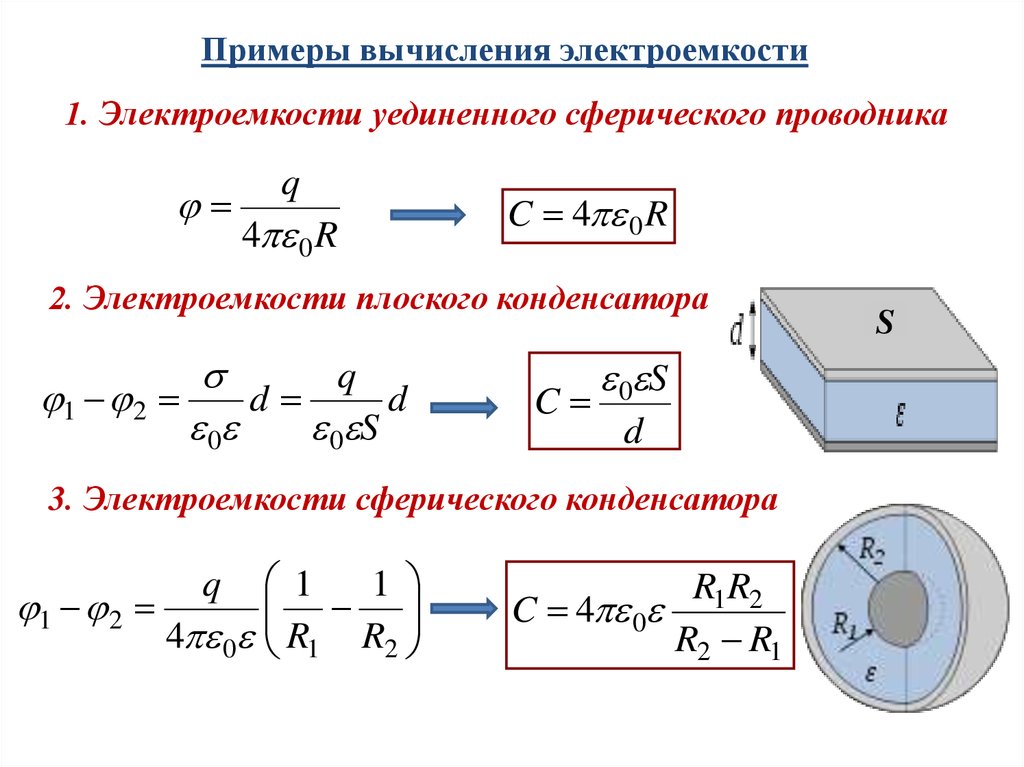
Примеры вычисления электроемкости
1. Электроемкости уединенного сферического проводника
q
4 0 R
C 4 0 R
2. Электроемкости плоского конденсатора
q
1 2
d
d
0
0 S
C
0 S
d
3. Электроемкости сферического конденсатора
1
1
1 2
4 0 R1 R2
q
R1R2
C 4 0
R2 R1
SS

8.

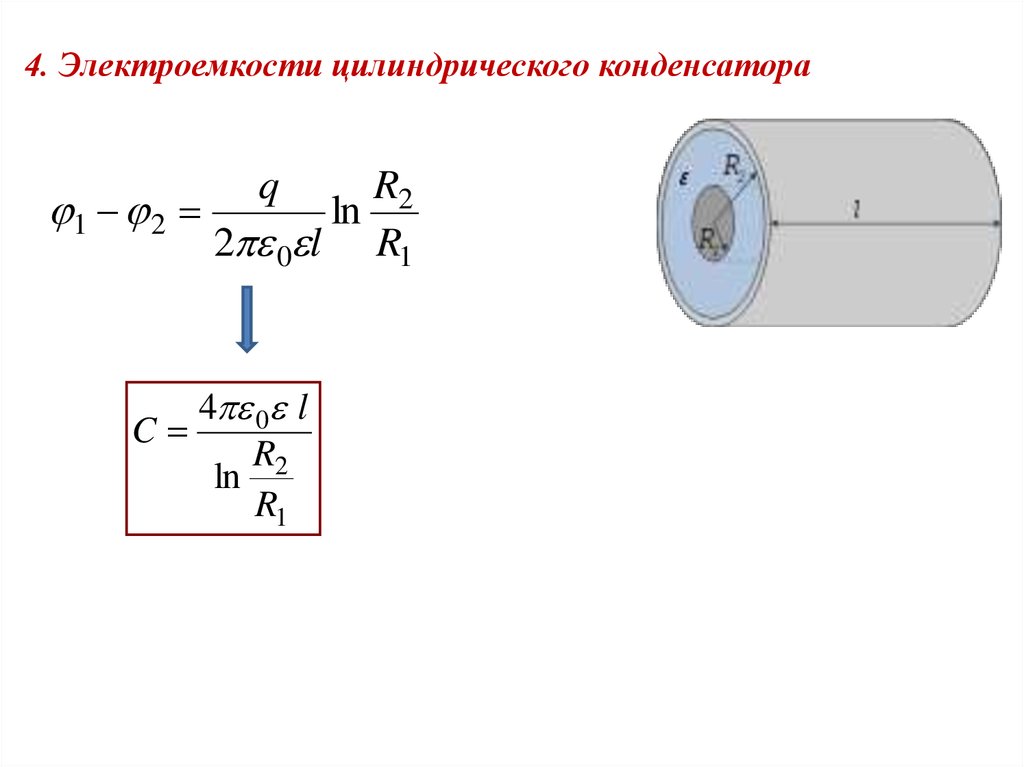
4. Электроемкости цилиндрического конденсатора
q
R2
1 2
ln
2 0 l R1
4 0 l
C
R2
ln
R1

9.

4. Энергия электростатического поля
1
1
1 2
2
W q C
q
2
2
2C
Уединенного проводника
1
1
1 2
2
W qU CU
q
2
2
2C
0 S
C
1
2
W CU
d
2
U Ed
Конденсатора
0 E 2
2
Sd
0 E 2
2
V
W 0 E
D
ED ED Объемная плотность
энергии
V
2
2 0
2
2
W ( r )dV Вычисление энергии в случае неоднородного поля
2
V
2