Аксиома параллельных прямых. Доказательство от противного

1.

2
3
6
37о

2.

3.

4.

5.

6.

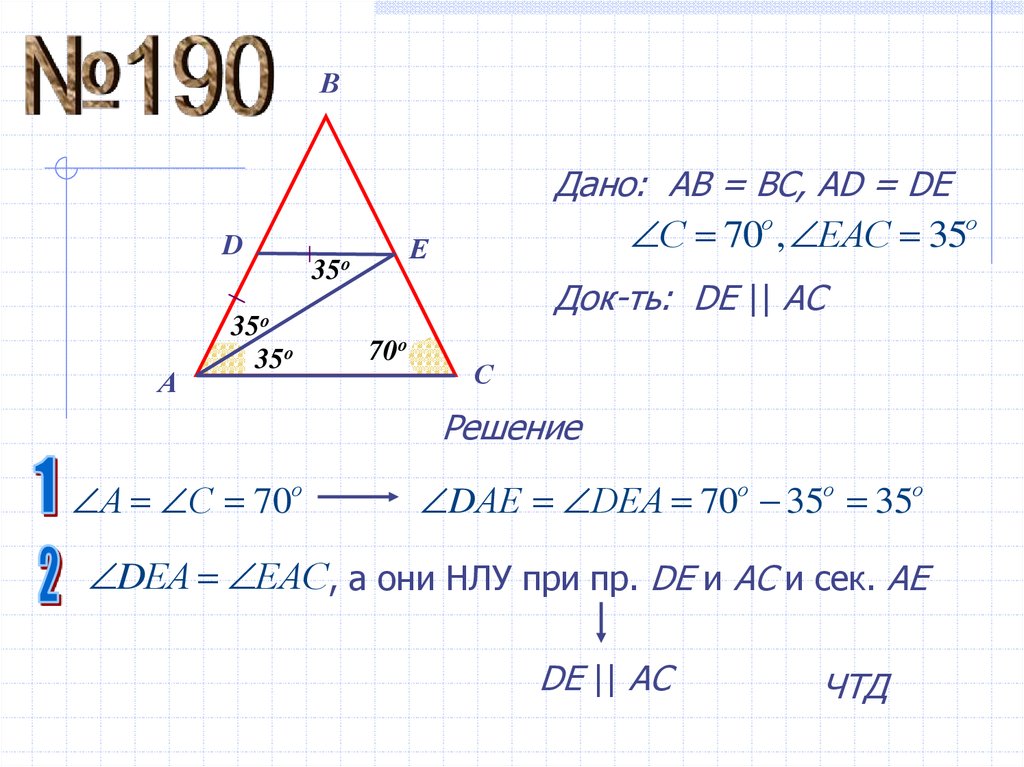
В
Дано: АВ = ВС, АD = DЕ
D
А
Е
35о
35о
35о
С 70о , ЕАС 35о
Док-ть: DЕ || АС
70о
С
Решение
А С 70о
DАЕ DЕА 70о 35о 35о
DЕА ЕАС, а они НЛУ при пр. DЕ и АС и сек. АЕ
DЕ || АС
ЧТД

7.

В
Дано: СD – бис-са ВСЕ
А 40о , ВСЕ 80о
D
Док-ть: АВ || СD
40о
40о
40о
С
А
Е
Решение
DСЕ 40 (СD бис са )
о
А 40 (по усл.)
о
DСЕ А(СУ )
АВ || СD
ЧТД

8.

03.01.2019
К л а с с н а я р а б о т а.
Доказательство от противного.
Аксиома параллельных
прямых

9. В Древней Греции всех ораторов и политиков учили геометрии. На дверях школы Платона было написано «Да не войдет сюда не знающий

геометрии».
Геометрия учит
доказывать,
а
речь
человека
убедительна
только тогда, когда он
доказывает свои выводы.

10. В своих рассуждениях люди часто используют способ доказательства, который называется доказательством от противного.

11.

Врач
после
осмотра
больного
ребенка
доказывает
родителям, почему у
него нет кори: если бы
у ребенка была корь, то
на его теле была бы
сыпь, но её нет.
Значит, у ребенка нет
кори.

12.

Разведчики
получили задание:
выяснить,
находится ли в
данном селе
танковая колонна
противника.
Командир разведки доказывает: если бы в селе
была танковая колонна, то были бы следы
гусениц, а их не обнаружили, значит, в селе
нет танковой колонны.

13.

14.

В чем же заключается сущность способа
доказательства от противного?
1. Делается предположение, противное тому, что требуется
доказать
Предположим: - Пусть…
2. Выясняется, что следует из сделанного предположения на
основании известных фактов
Рассуждаем: - Тогда…
3. Устанавливается противоречие между тем, что
утверждается в одном предложении, и его отрицании в
другом
Противоречие: - Это противоречит…
4. Делается вывод: предположение неверно, а верно то, что
требовалось доказать
Вывод: - Значит…

15.

1 2 156о
Доказать: 1 и 2 – не могут быть смежными
Дано:
Доказательство
Пусть
1 и 2 – смежные
о
1
2
180
Тогда
(свойство смежных углов)
Это противоречит условию задачи:
1 2 156
о
Значит , предположение 1 и 2 – смежные – неверно,
т.е. 1 и 2 – не могут быть смежными

16.

Дано: А, В, С – точки прямой а; АВ = 5 см, АС = 2 см,
ВС = 7 см
Доказать: точка С не лежит между точками А и В
Доказательство
Пусть точка С лежит между точками А и В
Тогда
АВ = АС + СВ
Это противоречит условию задачи: 5 ≠ 2 + 7
Значит , точка С не лежит между точками А и В

17. Аксиома

- это утверждение о свойствах
геометрических фигур, не требующее
доказательствах.
Теорема – это утверждение,
требующее доказательства.

18. Аксиома

Через любые две
точки проходит
прямая, и притом
только одна.

19.

Аксиома параллельности и следствия из неё.
c
А
Через точку, не лежащую на данной
b прямой, проходит только одна прямая,
параллельная данной.
а
с
а
b
Если прямая пересекает одну из
двух параллельных прямых, то она
пересекает и другую.
a II b, c b → c a
Следствие 1.
Если две прямые параллельны
третьей прямой, то они параллельны.
a II с, b II с → a II b
Следствие 2.