Similar presentations:
Свойства цилиндра. Выпуклый и прямой цилиндр
1.
Автор: Разина Аннаученица 11 «В» класса.
Руководитель: Самсонова Мария Николаевна
учитель математики.
2.
–
–
–
–
–
–
–
–
Введение.
Основная часть.
Что называют цилиндром? (из истории).
Различные определения.
Выпуклый цилиндр.
Свойства цилиндра.
Прямой цилиндр
Площадь поверхности цилиндра.
Объем цилиндра
Решение задач.
Заключительная часть.
Используемая литература.
3.
BP
M
О
M
N
A
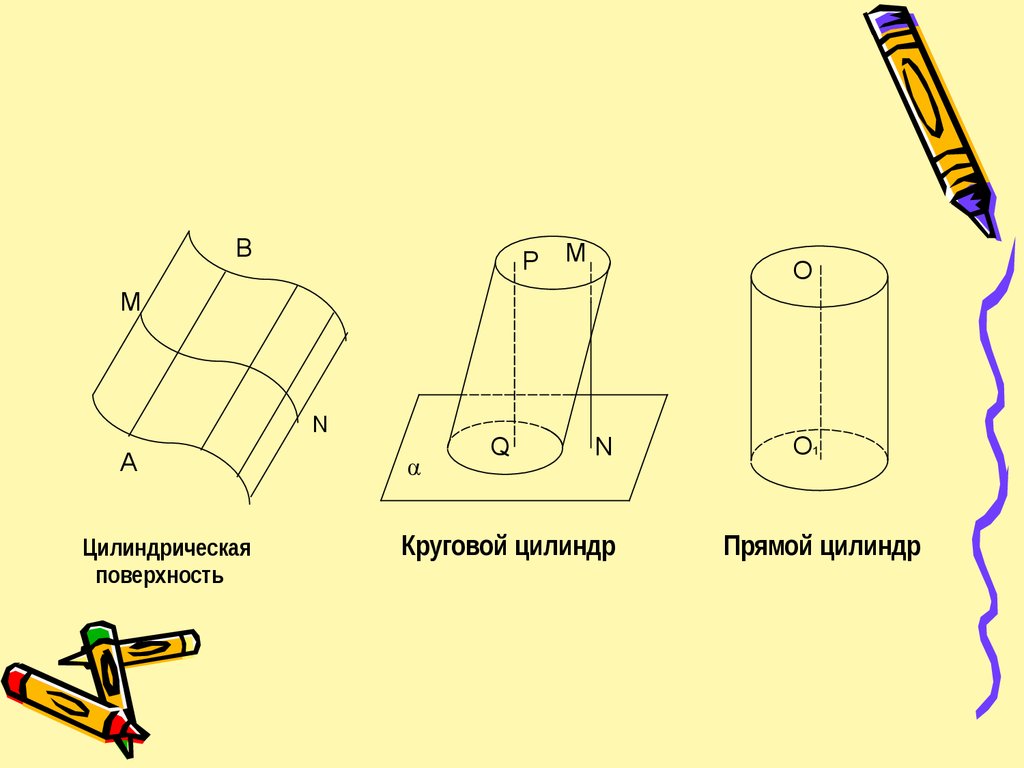
Цилиндрическая
поверхность
α
Q
N
Круговой цилиндр
О1
Прямой цилиндр
4.
X′Y′
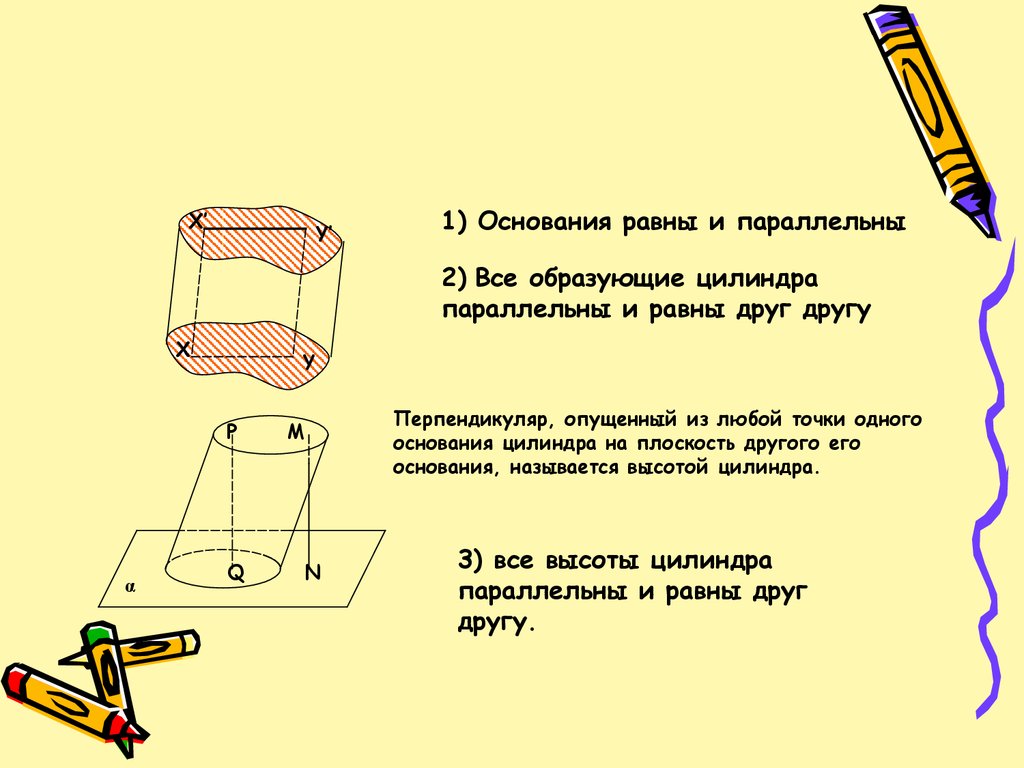
1) Основания равны и параллельны
2) Все образующие цилиндра
параллельны и равны друг другу
X
Y
P
α
Q
M
N
Перпендикуляр, опущенный из любой точки одного
основания цилиндра на плоскость другого его
основания, называется высотой цилиндра.
3) все высоты цилиндра
параллельны и равны друг
другу.
5.
О′F′′
α′′
F′
α′
F
α
О
1) Если секущая плоскость проходит
через ось цилиндра, то сечение
представляет собой прямоугольник ,
две стороны которого – образующие, а
две другие – диаметры оснований
цилиндра. Такое сечение называется
осевым.
2) Все сечения цилиндра плоскостями
параллельными плоскости основания,
равны основаниям цилиндра между собой.
6.
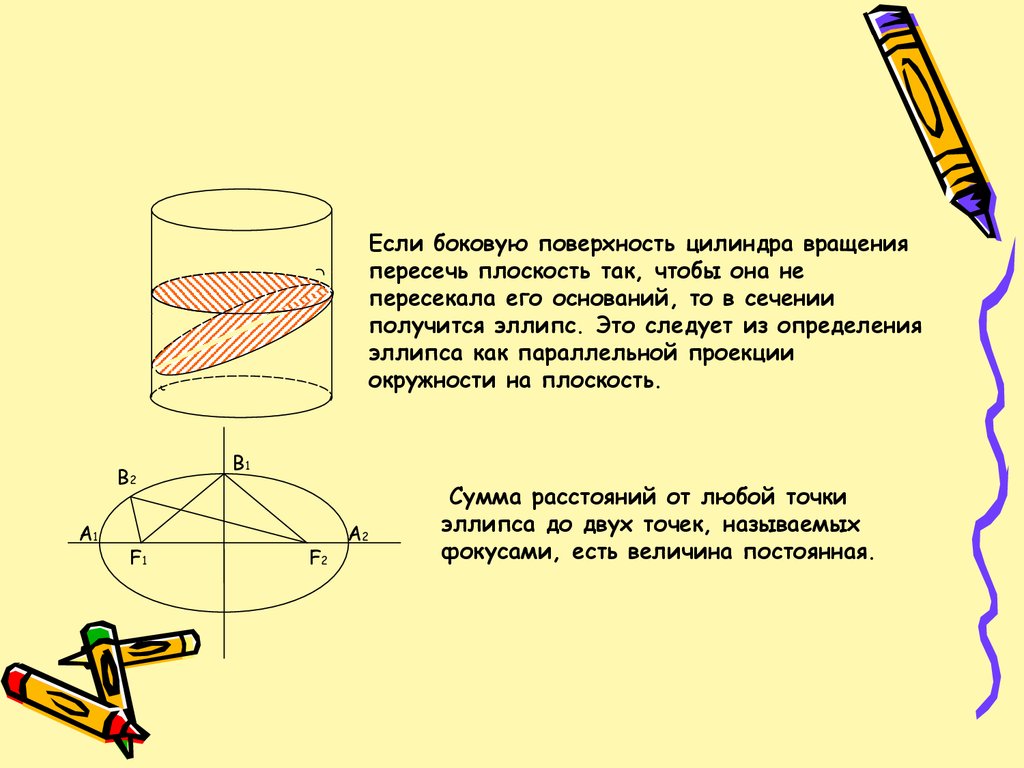
Если боковую поверхность цилиндра вращенияпересечь плоскость так, чтобы она не
пересекала его оснований, то в сечении
получится эллипс. Это следует из определения
эллипса как параллельной проекции
окружности на плоскость.
B2
A1
F1
B1
F2
A2
Сумма расстояний от любой точки
эллипса до двух точек, называемых
фокусами, есть величина постоянная.
7.
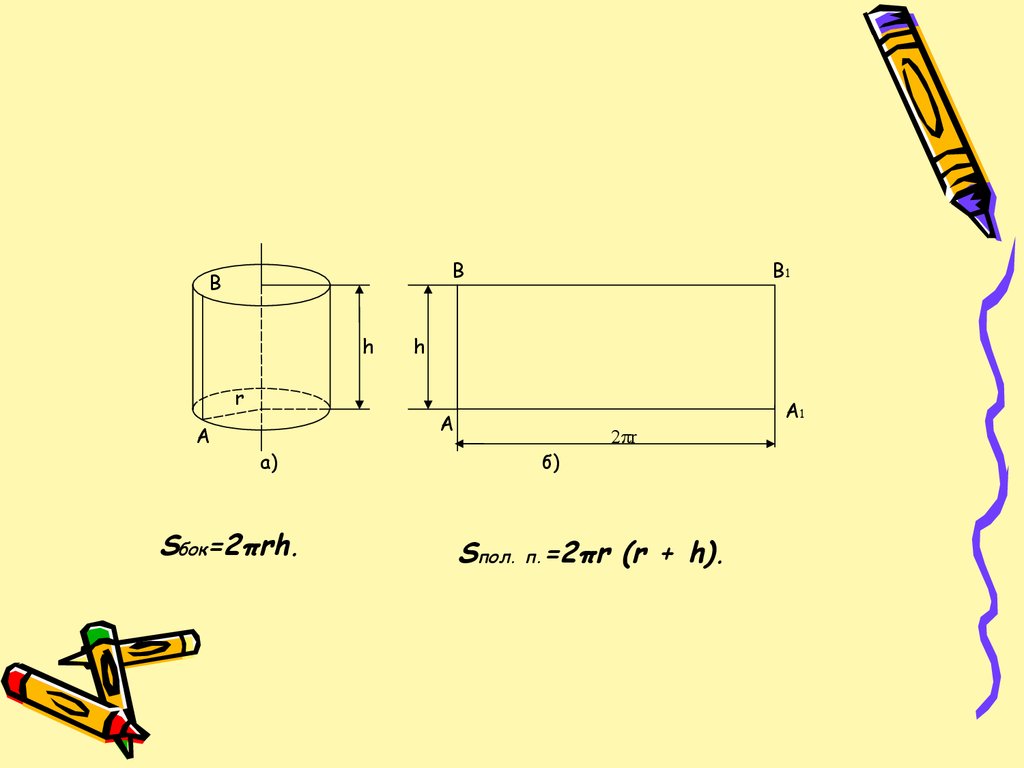
BB
h
r
A
B1
h
A1
A
a)
Sбок=2πrh.
б)
2πr
Sпол. п.=2πr (r + h).
8.
hh
h
r
r
r
Объем цилиндра равен произведению площади основания на высоту.
V = πr²h.
9.
Высота цилиндра равна Н, радиус его основания равен R. В цилиндр помещена пирамида,высота которой совпадает с образующей АА1 цилиндра, а основанием служит равнобедренный
треугольник АВС (АВ=АС), вписанный в основание цилиндра. Найти площадь боковой
поверхности пирамиды, если А = 120°.
Дано: цилиндр с высотой H и радиусом R, вписана
пирамида, образующая АА1 – высота
пирамиды,
АВС р/б, АВ=АС, АВС – вписан в основание цилиндра,
угол А = 120°.
Найти: Sбок пирамиды.
A1
O1
B
D
A
C
O
Решение:
1)Проведем AD ┴ BC и соединим точки А1 и D. Согласно
теореме , имеем А1D┴ BC. Так
как дуга CAB содержит 120° , а дуги АС и АВ – по 60° , то
ВС = R 3 , АВ = R .
2)В ∆ ABD имеем AD = R/2 . Далее, из ∆AA1D получим
A1D = ½ R² ²
Следовательно SА1АВ = ½ АВ · АА1 = ½ RH
SА1ВС = ½ ВС · А1D = ½ R 3 · ½ R² ²
3) Sбок = 2 SА1АВ + SА1ВС = RH + ¼ R
= R/4(4H + 3R² ² ).
Ответ: R/4(4H +
3R² ² ).
=¼R
3R² ² =
3R² ²
10.
Высота цилиндра равна 12 см. Через середину образующей цилиндра проведена прямая,пересекающая ось цилиндра на расстоянии 4 см от нижнего основания. Эта прямая пересекает
плоскость, содержащую нижнее основание цилиндра, на расстоянии 18 см от центра нижнего
основания. Найдите радиус основания цилиндра.
Дано: цилиндр, высота О1О2 = 12 см,
В – середина образующей М1М2, АВ пересекает О1О2
в т.С, СО2 = 4 см, АО2 = 18 см.
M1
O1
Найти: R основания.
B
М2
C
┐
R
┐
O2
A
Решение:
Проведем плоскость через данную в условии
задачи прямую АВ и ось цилиндра О1О2 . Эта
плоскость содержит также образующую М1М2, в
которой пересекается с поверхностью
цилиндра. Длина М1М2 равна высоте цилиндра,
т.е. М1 М2 = 12см, тогда по условию ВМ2 = 6 см.
М1 М2 || О1О2, значит, ВМ 2 А СО2 А 90 , еще
у треугольников ∆АВМ2 и ∆АСО2 общий угол А,
и значит они подобны.
Отсюда СО
АО 2
4
18
2
, т.е.
,
ВМ 2 АМ 2
6 18 R
4(18 R ) 6 18,
4 R 36, R 9.
Ответ: 9см
11.
Автор: Разина Аннаученица 11 «В» класса.
Руководитель: Самсонова Мария Николаевна
учитель математики.





 mathematics
mathematics








