Производная и ее приложения

1. Производная и ее приложения.

Приращение функции. Физический
смысл производной. Вычисление
производной по определению

2. Приращение функции

1) Сформулируйте определения
приращения
аргумента
и
приращения функции в данной точке
x0.
?
2) От чего зависит приращение
функции при каждом
фиксированном x0?
3) Что показывает на
графике отношение
f ( x 0 )
x

3. Физический смысл производной, рассмотрим падение тела с некоторой высоты

• рассмотрим промежуток t от момента t0 до t = t0 + t.
Тогда S(t0) = S(t0 + t) – S(t0) = ... = gt0 t + g( t)2, то
есть, при фиксированном t0 S(t0) зависит только
от t ! Для рассматриваемой функции: t –
приращение аргумента в точке t0; S(t0) –
приращение функции в этой точке. Средняя скорость
S ( t 0 )
• движения на [t0; t0 + t] равна: Vср.
= gt0 + 1 g t
1
t
2
= V0 + 2 g t. Пусть t 0, тогда
1
lim Vс р. lim V0 g t V0
t 0
t 0
2
Таким образом, для каждого фиксированного
S (t 0 )
lim
V0
момента времени t0
t 0
t
–равен некоторому числу, которое называется мгновенной
скоростью падения тела в момент времени t0!

4. Определение

• Производной функции в точке x0
называется предел отношения
приращения функции к приращению
аргумента, если приращение
аргумента стремится к нулю.
f ( x 0 )
f ( x 0 x ) f ( x 0 )
f '( x 0 ) lim
lim
x 0
x 0
x
x

5. Определения.

• 1) Функция называется дифференцируемой в
точке x0, если f’(x0).
• 2) Функция называется дифференцируемой на
множестве I, если она дифференцируема в
каждой точке из этого множества.
• Пусть функция y = f(x) дифференцируема на I.
Тогда x0 I f’(x0). Соответствие {x0} {f’(x0)}
определяет новую функцию, которая
называется производной функции y = f(x) и
обозначается f’(x).
• В чем различие f’(x) и f’(x0)? [функция и число].
Операция вычисления производной функции
называется дифференцированием функции.

6. Вычисление производных по определению

• 1) f(x) = C.
f(x0) = f(x0 + x) – f(x0) = C – C = 0;
.
Таким
образом,.
f ( x 0 )
f '( x 0 ) lim
lim 0 0
(С)’ = 0
x 0
x 0
x
• 2) f(x) = kx + b.
• f(x0) = f(x0 + x) – f(x0) = k(x0 + x) – kx0 = k x;
f ( x 0 )
lim k k Таким образом,
• f '( x 0 ) lim
.
x 0
x 0
x
.
(kx + b)’ = k

7. Алгоритм нахождения производной:

• Зафиксировать значение х0 и найти f(x0)
• Дать аргументу х0 приращение х ,и найти
f(х0+ х)
• Найти приращение у= f(х0+ х) - f(х0)
• Составить отношение у/ х
• Вычислить
f ( x 0 )
f ( x 0 x ) f ( x 0 )
f '( x 0 ) lim
lim
x 0
x 0
x
x

8. Вычислить по определению производные

• 3) f(x) = ax2 + bx + c
• 4) f(x) =
x . f’(0) – не существует
.
(
x )’ =
1
2 x
(ax2 + bx + c)’ = 2ax + b

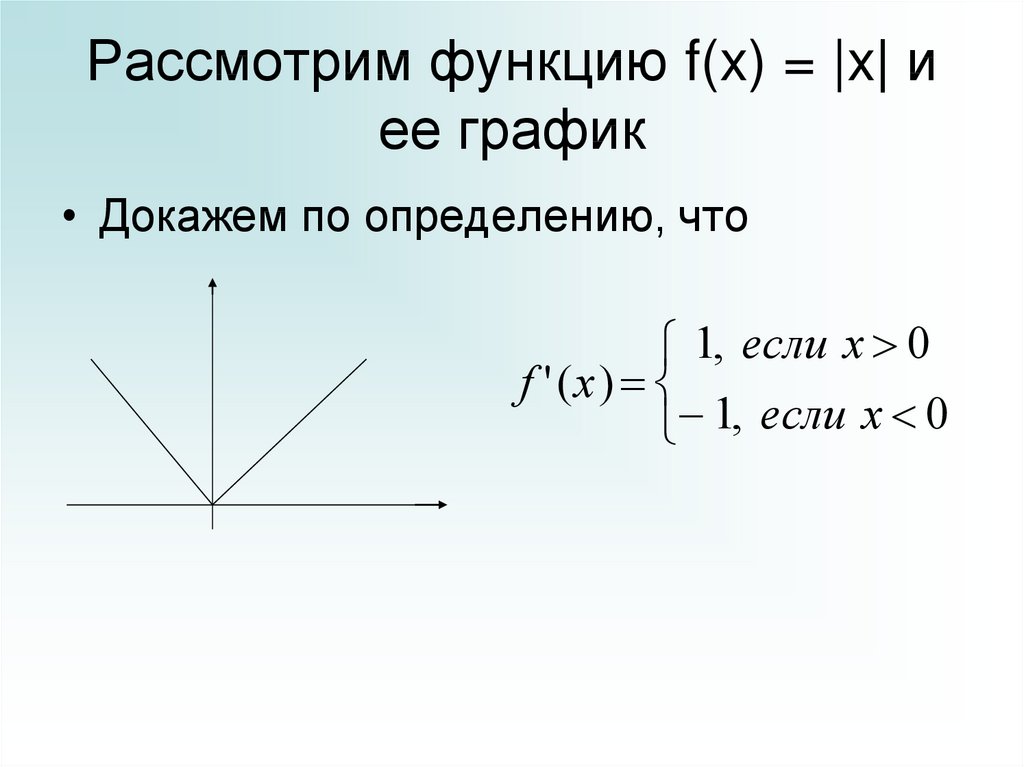
9. Рассмотрим функцию f(x) = |x| и ее график

• Докажем по определению, что
1, если x 0
f '( x )
1, если x 0

10.

А) Пусть x0 > 0, тогда выберем x так, чтобы
x0 + x > 0. f(x0) = |x0 + x| – |x0| = x;
f ( x 0 )
f '( x 0 ) lim
lim 1 1
x 0
x 0
• .
x
Б) Пусть x0 < 0, тогда выберем x так, чтобы
x0 + x < 0. Аналогично получим, что . f '( x ) 1
0
В) Пусть x0 = 0, тогда f(x0) = |x0 + x| – |x0|=| x|.
f ( x 0 )
x
,
не существует, поэтому
lim
x 0
x
lim
x 0
x
• данная функция не дифференцируема в
нуле.

11.

• F(x) = |x2 – 6x + 5|.
• А) Постройте график функции.
• Б) Найдите f’(2) и f’(6).
• B) (по вариантам) Докажите, что в точках
x0 = 1 и x0 = 5 функция не дифференцируема

12.

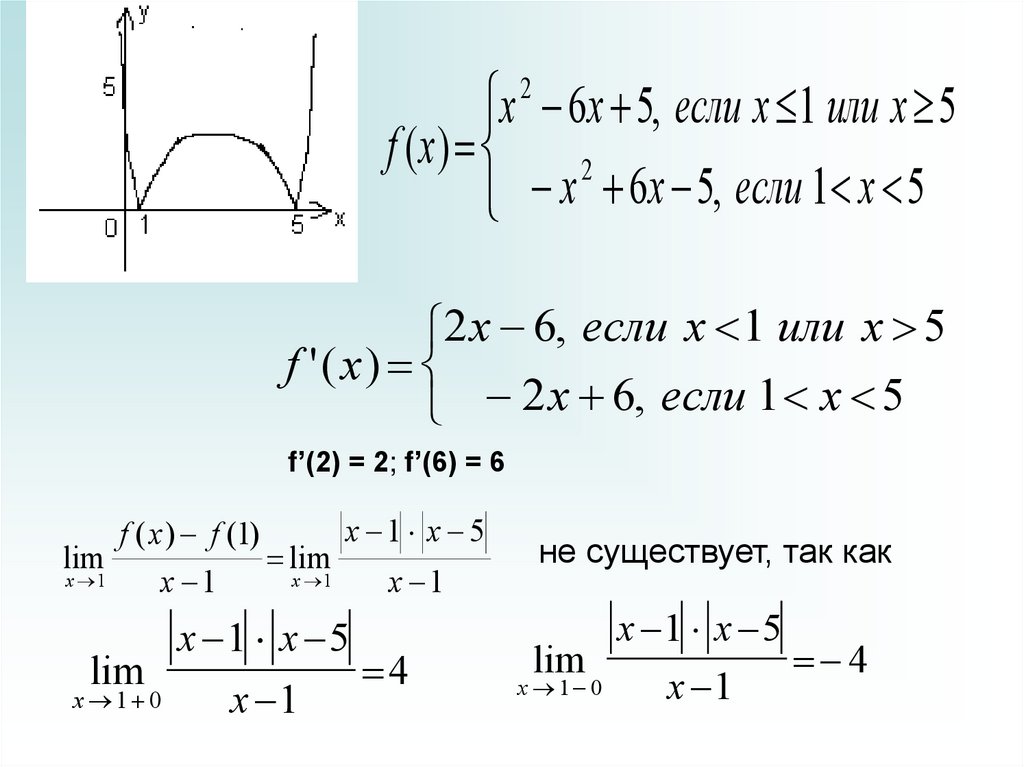
x 6x 5, если x 1 или x 5
f (x )
2
x 6x 5, если 1 x 5
2
2 x 6, если x 1 или x 5
f '( x )
2 x 6, если 1 x 5
f’(2) = 2; f’(6) = 6
x 1 x 5
f ( x ) f (1)
lim
lim
x 1
x 1
x 1
x 1
lim
x 1 0
x 1 x 5
x 1
4
не существует, так как
lim
x 1 0
x 1 x 5
x 1
4

13.

x 1 x 5
f ( x ) f ( 5)
lim
lim
x 5
x 1
x 5
x 5
не существует, так как
lim
x 5 0
x 1 x 5
x 5
4
lim
x 5 0
x 1 x 5
x 5
4

14. Домашнее задание

• Выучить стр163 п1,2,3 и записи
• Вып.№392 (3,5,7) №393(1,2)
• Cоставить таблицу производных.
Вопросы по теории:
1)Сформулируйте определение приращения функции и приращения аргумента.
2) определение производной функции в точке.
3)Физический смысл производной
4)Как называется операция нахождения производной?
5)Какая функция называется дифференцируемой в точке?.
6)Какая функция называется дифференцируемой на отрезке?
7)Алгоритм вычисления производной.
8) Вычислять по определению производные простейших функций.